鳥取大物理'00年[4]
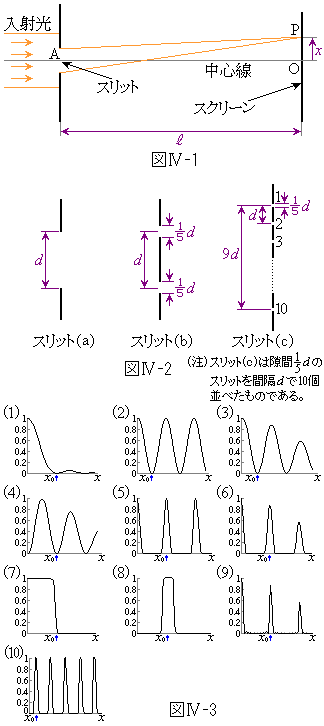 図Ⅳ-1に示す配置の光の干渉実験において、スリットの位置Aに図Ⅳ-2に示す形状のスリット(a),(b)および(c)を置いた場合、それぞれスクリーン上にどのような干渉縞が生じるか、図Ⅳ-3の(1)~(10)に示す図形より最も近いと思われるものを選べ。また、選んだ図形のx軸上の位置
図Ⅳ-1に示す配置の光の干渉実験において、スリットの位置Aに図Ⅳ-2に示す形状のスリット(a),(b)および(c)を置いた場合、それぞれスクリーン上にどのような干渉縞が生じるか、図Ⅳ-3の(1)~(10)に示す図形より最も近いと思われるものを選べ。また、選んだ図形のx軸上の位置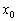 の近似値をλ,
の近似値をλ,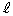 ,d等を用いて表せ。
,d等を用いて表せ。
ただし、入射光は平行な単色光であり、スリットおよびスクリーンは入射光に対して垂直に置かれているものとする。また、装置全体は中心線に対して上下対称である。ここでは、目安として波長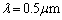 ,スリットとスクリーンとの間の距離
,スリットとスクリーンとの間の距離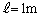 ,図Ⅳ-2におけるdは長さを示しており
,図Ⅳ-2におけるdは長さを示しており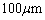 程度を考えよ。なお、図Ⅳ-3の図形は中心線より片側の中心付近の光の強さを示しており、高さは最高強度を1としている。また、x軸は必ずしも同一の尺度とは限らない。
程度を考えよ。なお、図Ⅳ-3の図形は中心線より片側の中心付近の光の強さを示しており、高さは最高強度を1としている。また、x軸は必ずしも同一の尺度とは限らない。
必要なら次の近似式を用いよ。zが1に比べて充分に小さいとき、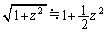 。
。 が十分小さいとき、
が十分小さいとき、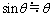 および
および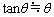 。
。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 回折格子の単スリット効果(中央部分の明線が最も明るく、両側に行くに従って明線が暗くなる)の問題です。
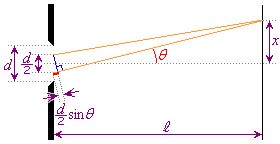 (a) 単スリットの場合、スリット上半分を通過する光と下半分を通過する光に分け、2光の干渉を考えます。単スリットでは干渉の効果は弱いので1次の暗線の方向のみを考えます。
(a) 単スリットの場合、スリット上半分を通過する光と下半分を通過する光に分け、2光の干渉を考えます。単スリットでは干渉の効果は弱いので1次の暗線の方向のみを考えます。スリット上半分の中間の点と下半分の中間の点の間の距離は、右図より、スリット間隔の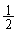 で
で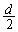 です。
です。
スリットを通過した後、角θ の方向に進む2光の経路差は、右図より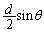
スリットとスクリーンの距離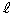 はスクリーン上で中心線からの距離xに比べて十分に大きいので、
はスクリーン上で中心線からの距離xに比べて十分に大きいので、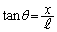 のθ は十分に小さく、
のθ は十分に小さく、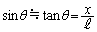 ,よって、2光が弱め合うのは2光の経路差が半波長の場合だとして、
,よって、2光が弱め合うのは2光の経路差が半波長の場合だとして、 ∴ 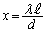 従って、
従って、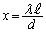 においては、2光が干渉して弱め合い、光の強さは0になります。xが
においては、2光が干渉して弱め合い、光の強さは0になります。xが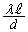 を越えると、弱め合う条件が緩和されて若干明るくなりますが、強め合うわけではなく明線ができるわけではありません。また、スリットを通過した後直進する光は、スクリーン中央に明るい部分を作ります。この状況を表すグラフは(1) ......[答] です。また、
を越えると、弱め合う条件が緩和されて若干明るくなりますが、強め合うわけではなく明線ができるわけではありません。また、スリットを通過した後直進する光は、スクリーン中央に明るい部分を作ります。この状況を表すグラフは(1) ......[答] です。また、 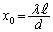 ......[答]
......[答]
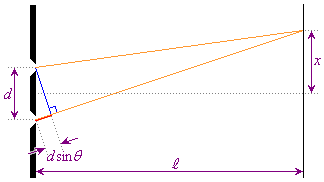 (b) 二重スリットの場合、上のスリットを通過した光と下のスリットを通過した2光の干渉を考えます。
(b) 二重スリットの場合、上のスリットを通過した光と下のスリットを通過した2光の干渉を考えます。隣接スリットの間隔はdです。スリットを通過した後、角θ の方向に進む2光の経路差は、(a)と同様の近似を行い、右図より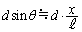 2光が強め合うのは2光の経路差が波長の整数倍だとして、
2光が強め合うのは2光の経路差が波長の整数倍だとして、 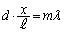 (m:整数)
(m:整数)∴ 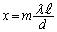 従って、
従って、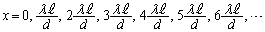 においては、2光が干渉して強め合い、明線ができます。二重スリットの干渉では、明線がぼやけていて幅が広くなります。また、
においては、2光が干渉して強め合い、明線ができます。二重スリットの干渉では、明線がぼやけていて幅が広くなります。また、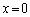 は明線です。
は明線です。
ですが、各スリットにスリット自体の幅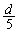 があるために、(a)で考えた単スリットの効果を考慮する必要があります。(a)のd→
があるために、(a)で考えた単スリットの効果を考慮する必要があります。(a)のd→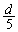 として、
として、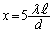 においては、各スリットの上半分と下半分を通過した光が強め合って強度が0になります。従って、この効果のために、二重スリットによってできる明線は、mが
においては、各スリットの上半分と下半分を通過した光が強め合って強度が0になります。従って、この効果のために、二重スリットによってできる明線は、mが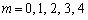 と変化すると次第に強度が落ちてきます。
と変化すると次第に強度が落ちてきます。
以上の状況を表すグラフは(3) ......[答] です。
また、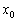 は最も
は最も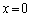 に近い暗線の位置で、弱め合う条件:
に近い暗線の位置で、弱め合う条件: 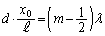 (m:整数)
(m:整数)において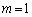 として、
として、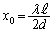 ......[答]
......[答]
(c) スリットの数が10個になると、隣接する2つのスリットを通過する光が強め合う条件は二重スリットと同じで、mを整数として、
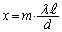 ・・・①
・・・①に明線ができます。
ですが、隣接していないスリットを通過する光も干渉します。kを整数として間隔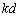 の2つのスリットを通過する2光が強め合う条件は、
の2つのスリットを通過する2光が強め合う条件は、 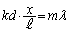 (m:整数)
(m:整数)∴ 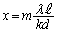
mがkの倍数になるときには、①の位置と重なり、明線は隣接スリット以外のスリット同士でも強め合って強度を増します。
弱め合う条件は、 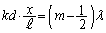 (m:整数)
(m:整数)∴ 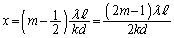 暗線条件では、分子の奇数
暗線条件では、分子の奇数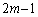 は分母の偶数
は分母の偶数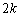 の倍数にはならないので、①の位置に重なりません。①以外の位置の光の強度を弱める効果をもっています。
の倍数にはならないので、①の位置に重なりません。①以外の位置の光の強度を弱める効果をもっています。
結果的に、スリットの数を増やすと、明線の位置の強度を上げ、明線位置以外の光の強度を弱めることになり、明線が鋭くなります(多重スリットを参照。これが回折格子を使って波長測定を行う意味です)。
以上の状況だけであれば、(10)のグラフになるはずですが、各スリットに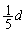 の幅があるので、(b)と同様に、単スリットの効果で、明線は、mが
の幅があるので、(b)と同様に、単スリットの効果で、明線は、mが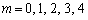 と変化すると次第に強度が落ちてきます。この状況を表すグラフは(9) ......[答] です。
と変化すると次第に強度が落ちてきます。この状況を表すグラフは(9) ......[答] です。
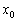 は、①の
は、①の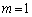 の位置になり、
の位置になり、 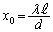 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。