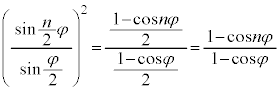���d�X���b�g�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�����ł́A2�d�X���b�g����X���b�g�̐��𑝂₵�Ă����Ƃ��̉�܌����������l���܂��B
2�d�X���b�g�ł́A2�̃X���b�g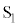 �C
�C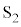 ����X�N���[����̓_P�ɓ��B��������o�H���́A�X���b�g�Ԋu��d�C�X���b�g�ʒu����X�N���[���܂ł�������l�C�X�N���[����ɗ��X���b�g�����������̓_�����_O�Ƃ���x�����Ƃ�A�_P�����W��x�C���X���b�g��ʉ߂������ƃX�N���[���ɗ��Ă��@���Ƃ̂Ȃ��p���Ƃ���θ (l�͏[���ɑ傫���Aθ �͔����Ȋp�Ƃ��܂�)�Ƃ��āA
����X�N���[����̓_P�ɓ��B��������o�H���́A�X���b�g�Ԋu��d�C�X���b�g�ʒu����X�N���[���܂ł�������l�C�X�N���[����ɗ��X���b�g�����������̓_�����_O�Ƃ���x�����Ƃ�A�_P�����W��x�C���X���b�g��ʉ߂������ƃX�N���[���ɗ��Ă��@���Ƃ̂Ȃ��p���Ƃ���θ (l�͏[���ɑ傫���Aθ �͔����Ȋp�Ƃ��܂�)�Ƃ��āA
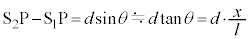
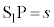 �Ƃ��āA
�Ƃ��āA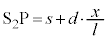 �Ȃ̂ŁA2�̃X���b�g
�Ȃ̂ŁA2�̃X���b�g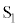 �C
�C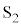 ����P�ɓ��B������g���ψ����A
����P�ɓ��B������g���ψ����A
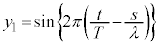 �C
�C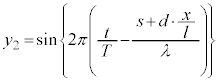 �@����@
�@����@
���̂����A�E�ӂ�sin�͈ʑ���t ���܂ނ̂��P�U����\���A�P�U�����U���Ɋ�^����̂́At ���܂܂Ȃ�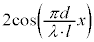 �ł��B
�ł��B
 �_P�ɂ��������邳�́A�����G�l���M�[���x�ɔ�Ⴕ�A���g���U����2��ɔ�Ⴗ��̂ŁA
�_P�ɂ��������邳�́A�����G�l���M�[���x�ɔ�Ⴕ�A���g���U����2��ɔ�Ⴗ��̂ŁA
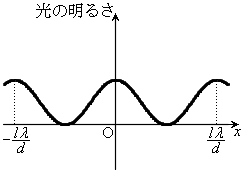
�ɔ�Ⴗ��ƍl�����܂��B�������邳��x�Ƃ̊W���E�}�̃O���t�Ɏ����܂����B
�܂�A2�d�X���b�g�ł́A�����A�Ð��ƌ����Ă��A�ڂ�[���Ɩ��邭�A�܂��A�ڂ�[���ƈÂ��A�ǂ��������ʒu�ŁA�ǂ����Ð��ʒu�Ȃ̂��͂����肵�Ȃ��̂ł��B�����O�̊������ɂ��A�����Ԋu��������g�������߂邱�Ƃ��ł��܂������A�L������1�����x�̂����悻�̒l�����߂邱�Ƃ͂ł��܂����A�����Ȕg���̑�����s�����Ƃ͂ł��܂���B
�����ŁA�X���b�g�̐���1���₵�āA3�ɂ��邱�Ƃ��l���܂��B3�ڂ̃X���b�g����_P�ɂ���Ă�����g���ψ�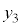 ���A���̐i������
���A���̐i������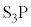 ��
��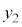 ��
��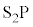 ��肳���
��肳���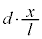 ���������Ȃ�Ƃ��ć@�Ɠ��l�ɁA
���������Ȃ�Ƃ��ć@�Ɠ��l�ɁA
�Ƃ���ƁAP�_�ł��ψ��́A3���g���d�ˍ��킹�āA
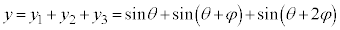 �@����B
�@����B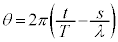 �C
�C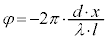 �@����C�@�Ƃ��܂��B
�@����C�@�Ƃ��܂��B
��p���āAP�_�ł��ψ��̎��B��ό`����ƁA
�C���A���̎���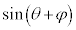 �̕���������t ���܂ނ̂ŁA�P�U����\���܂��B�P�U�����U���Ɋ�^����̂́At ���܂܂Ȃ�
�̕���������t ���܂ނ̂ŁA�P�U����\���܂��B�P�U�����U���Ɋ�^����̂́At ���܂܂Ȃ�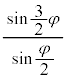 �ł��B
�ł��B
 �O�q�̂悤�ɁA�_P�ɂ��������邳�́A�U����2��ɔ�Ⴗ��̂ŁA�C���A
�O�q�̂悤�ɁA�_P�ɂ��������邳�́A�U����2��ɔ�Ⴗ��̂ŁA�C���A
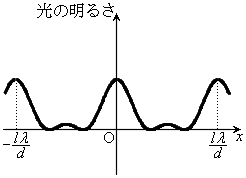
�ɔ�Ⴗ��ƍl�����܂��B�������邳��x�Ƃ̊W���A�E�}�̃O���t�Ɏ����܂���(�c���������k�߂Ă��܂�)�B���_�̓X���b�g�̐��ɂ�����炸�A�����ɂȂ邱�Ƃɒ��ӂ��Ă��������B
2�d�X���b�g�̂Ƃ��������ʒu�́A3�d�X���b�g�̂Ƃ��������ʒu�ɂȂ�܂����A2�d�X���b�g�̂Ƃ��̖����̒��Ԃɂ�▾�邢�������ł��Ă���̂��킩��܂��Bm�𐮐��Ƃ��āA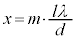 �̈ʒu�̋ɑ����ɑ�A���̊Ԃɂł��Ă����▾�邢�ɑ�ɑ�ƌ����܂��B
�̈ʒu�̋ɑ����ɑ�A���̊Ԃɂł��Ă����▾�邢�ɑ�ɑ�ƌ����܂��B
����ɃX���b�g�̐��𑝂₵��n�ɂ��Ă݂܂��Bk�Ԗ�(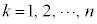 )�̃X���b�g����_P�ɂ���Ă�����g���ψ����A�@�C�B�Ɠ��l�ɁA
)�̃X���b�g����_P�ɂ���Ă�����g���ψ����A�@�C�B�Ɠ��l�ɁA
�Ƃ���ƁAP�_�ł��ψ��́An�̌��g���d�ˍ��킹�āA3�d�X���b�g�̂Ƃ��̇C�Ɠ��l�ɁA
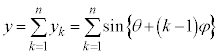 �@����D
�@����D
���g���āA�D�́A�א�2���őł����������āA
���̎���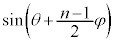 �̕���������t ���܂ނ̂ŁA�P�U����\���܂��B�P�U�����U���Ɋ�^����̂́A
�̕���������t ���܂ނ̂ŁA�P�U����\���܂��B�P�U�����U���Ɋ�^����̂́A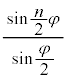 �ł��B
�ł��B
�_P�ɂ��������邳�́A�U����2��ɔ�Ⴗ��̂ŁA
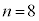 �̏ꍇ���A�E�}�̃O���t�Ɏ����܂���(�c���������k�߂Ă��܂�)�B���_�͖����ł��B
�̏ꍇ���A�E�}�̃O���t�Ɏ����܂���(�c���������k�߂Ă��܂�)�B���_�͖����ł��B
2�d�X���b�g�̂Ƃ��Ɠ��l�ɁAm�𐮐��Ƃ��āA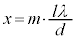 �̈ʒu�Ɏ�ɑ傪�ł��āA��ɑ�̊Ԃɏ����ȕ��ɑ傪6�ł��Ă��邱�Ƃ��킩��܂��Bn��傫�����邱�Ƃɂ���āA��ɑ�ƕ��ɑ�̍����傫���A��ɑ�͎���ɉs���Ȃ��Ă������Ƃ��킩��܂��B
�̈ʒu�Ɏ�ɑ傪�ł��āA��ɑ�̊Ԃɏ����ȕ��ɑ傪6�ł��Ă��邱�Ƃ��킩��܂��Bn��傫�����邱�Ƃɂ���āA��ɑ�ƕ��ɑ�̍����傫���A��ɑ�͎���ɉs���Ȃ��Ă������Ƃ��킩��܂��B
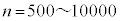 ���x�ɂ���ƁA��ɑ�͋ɂ߂ăV���[�v�ɂȂ�A�����Ԋu�������x�ɑ��肷�邱�Ƃ��\�ɂȂ�A�g���̑�����ɍs�����Ƃ��\�ɂȂ�܂��B���ꂪ�A�X���b�g���𑝂₵����܊i�q���g�����R�ł��B
���x�ɂ���ƁA��ɑ�͋ɂ߂ăV���[�v�ɂȂ�A�����Ԋu�������x�ɑ��肷�邱�Ƃ��\�ɂȂ�A�g���̑�����ɍs�����Ƃ��\�ɂȂ�܂��B���ꂪ�A�X���b�g���𑝂₵����܊i�q���g�����R�ł��B
�Ȃ��A���ۂɂ́A�X���b�g�̕��ɂ��P�X���b�g���ʂ̉e�����傫���A���_O�̎�ɑ傩��A�X�N���[�������Ɍ������āA��ɑ�͎���ɈÂ��Ȃ��Ă����܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  �@����@
�@����@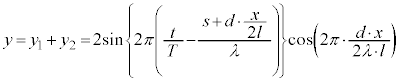
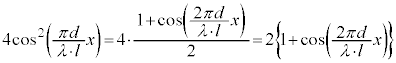
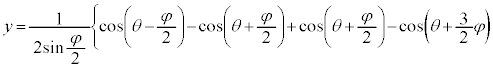
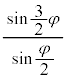 �ł��B
�ł��B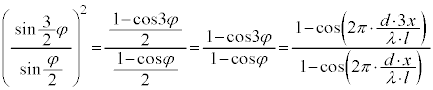
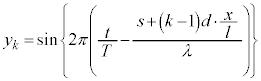
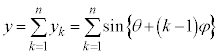 �@����D
�@����D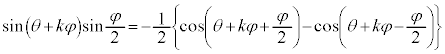
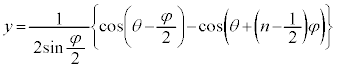
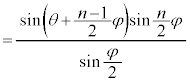
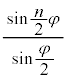 �ł��B
�ł��B