���嗝�H����'08�N[2]
���̕��͂̋ɂ����Ƃ��K���������܂��͐��l���A���ꂼ��L���B���l�͗L������2���œ�����B
�ȉ~(������)�Ƃ́A���ʏ�ŁA����2�_(�œ_�Ƃ���)����̋����̘a�����ł���_���������Ȑ��ł���B�P�v���[�̑�1�@���Ƃ��Ēm���Ă���悤�ɁA���z�n�̘f���̋O���͑��z���œ_��1�Ƃ���ȉ~�ł���B�������A�n���␅���̂悤�Șf���̑ȉ~�O���͂قډ~�Ƃ݂Ȃ��Ă悢���̂Ȃ̂ŁA�ȉ��ł͘f���̋O���͉~�O���Ƃ��Čv�Z���邱�Ƃɂ���B
�f���̎��ʂ�m�C�~�O���̔��a(�f���|���z�Ԃ̋���)��r�Ƃ���B�f��������v�œ����~�^�����Ă���Ƃ���ƁA���S�͂̑傫���� (1) �ł���B���̗͂͑��z�Ƙf���̊Ԃɂ͂��炭���L���͂ł���A���̑傫���́A���z�̎��ʂ�M�C���L���͒萔��G�Ƃ����Ƃ�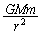 �ŗ^������B���̂��Ƃ���A�f���̌��]���x��
�ŗ^������B���̂��Ƃ���A�f���̌��]���x��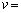 (2) �ƒ�߂���B���̒lv�ŋO���~���̒���
(2) �ƒ�߂���B���̒lv�ŋO���~���̒���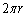 �����邱�Ƃɂ���āA���]���������߂邱�Ƃ��ł���B
�����邱�Ƃɂ���āA���]���������߂邱�Ƃ��ł���B
�n���Ƒ��z�̊Ԃ̋����� �Ƃ��āA�����P�ʂƂ��čl���邱�Ƃɂ���B���z����ؐ��܂ł̋�����
�Ƃ��āA�����P�ʂƂ��čl���邱�Ƃɂ���B���z����ؐ��܂ł̋�����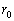 ��p�{�Ƃ���B����ƁA�ؐ��̌��]���x�͒n���̌��]���x�� (3) �{�ł��邱�ƂɂȂ�B���������āA�ؐ��� (4) �N�ő��z��1������v�Z�ɂȂ�B
��p�{�Ƃ���B����ƁA�ؐ��̌��]���x�͒n���̌��]���x�� (3) �{�ł��邱�ƂɂȂ�B���������āA�ؐ��� (4) �N�ő��z��1������v�Z�ɂȂ�B
�T���@��ł��グ�Đ}1�̂悤�ȋO���Ŗؐ��T�����������������B
���̒T���@�͖ؐ��Ɠ��l�ɃP�v���[�̖@���ɂ��������ĉ^��������̂Ƃ���B(�܂�A���z�ƒT���@�Ƃ̊Ԃ̖��L���͍͂l�����邪�A�n����ؐ��Ƃ������f���ƒT���@�Ƃ̊Ԃ̖��L���͖͂������Ă悢���̂Ƃ���B)
���̂��Ƃ��瓱����邱�Ƃ��A���ɍl���Ă݂悤�B
 �܂��P�v���[�̑�1�@�����A�T���@�̋O�������z���œ_��1�Ƃ���ȉ~�O���ł��邱�ƂɂȂ�B�n���̋O���ォ��o�������Ƃ��̑�����
�܂��P�v���[�̑�1�@�����A�T���@�̋O�������z���œ_��1�Ƃ���ȉ~�O���ł��邱�ƂɂȂ�B�n���̋O���ォ��o�������Ƃ��̑�����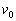 �Ƃ���ƁA�T���@�Ƒ��z�����Ԑ���������Z������
�Ƃ���ƁA�T���@�Ƒ��z�����Ԑ���������Z������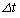 �̊Ԃɂ������ʐς́A�ߎ��I�ɂ͐}1�̎ΐ����{�����O�p�`�̖ʐ�
�̊Ԃɂ������ʐς́A�ߎ��I�ɂ͐}1�̎ΐ����{�����O�p�`�̖ʐ�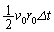 �ŗ^������B�T���@���ؐ��̋O���߂���ʉ߂���Ƃ��̑�����
�ŗ^������B�T���@���ؐ��̋O���߂���ʉ߂���Ƃ��̑����� �Ƃ���ƁA�P�v���[�̑�2�@��(�ʐϑ��x���̖@��)���
�Ƃ���ƁA�P�v���[�̑�2�@��(�ʐϑ��x���̖@��)���
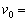 (5)
(5)
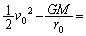 (6)
(6)  �͒n���̌��]���x�� (7) �{�łȂ���Ȃ�Ȃ����Ƃ��킩��B
�͒n���̌��]���x�� (7) �{�łȂ���Ȃ�Ȃ����Ƃ��킩��B
���z����T���@�܂ł̋����́A�n���̋O���ォ��o�������Ƃ��ɍŏ��l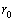 ���Ƃ�A�ؐ��̋O����ʉ߂���Ƃ��ɍő�l
���Ƃ�A�ؐ��̋O����ʉ߂���Ƃ��ɍő�l ���Ƃ�B���̍ŏ��l�ƍő�l�̕��ϒl
���Ƃ�B���̍ŏ��l�ƍő�l�̕��ϒl ��ȉ~�O���̔������Ƃ����B�P�v���[�̑�3�@�����A���]������2��͔�������3��ɔ�Ⴗ��B���������āA�T���@�͒n���̋O���ォ��o������ (8) �N��ɖؐ��̋O���ɓ��B���邱�ƂɂȂ�B
��ȉ~�O���̔������Ƃ����B�P�v���[�̑�3�@�����A���]������2��͔�������3��ɔ�Ⴗ��B���������āA�T���@�͒n���̋O���ォ��o������ (8) �N��ɖؐ��̋O���ɓ��B���邱�ƂɂȂ�B
��̓I�Ȑ��l���v�Z���Ă݂悤�B�ؐ��|���z�ԋ����͒n���|���z�ԋ����̖�5.2�{�ł���( )�B����āA�ؐ��̌��]�����͖� (9) �N�ł���B�n���̌��]���x�͖�
)�B����āA�ؐ��̌��]�����͖� (9) �N�ł���B�n���̌��]���x�͖�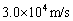 �ł���B������A�T���@���n���̋O���ォ��o������Ƃ��̑����́A
�ł���B������A�T���@���n���̋O���ォ��o������Ƃ��̑����́A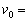 (10)
(10) 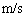 �C�ؐ��̋O���܂ł̍q�s���Ԃ͖� (11) �N�Ƌ��߂���B�������A
�C�ؐ��̋O���܂ł̍q�s���Ԃ͖� (11) �N�Ƌ��߂���B�������A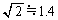 �C
�C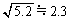 �C
�C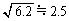 �Ƃ��Čv�Z����B
�Ƃ��Čv�Z����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�P�v���[�̖@���́A�ȉ��̂悤�ɂ܂Ƃ߂��܂��B
��1�@���F�f���͑��z��1�̏œ_�Ƃ���ȉ~�O����`���Ȃ���^������B
��2�@���F(�ʐϑ��x�ۑ���)���z���n�_�A�f�����I�_�Ƃ��铮�a�x�N�g�����P�ʎ��Ԃɒʉ߂���̈�̖ʐς͘f�����ƂɈ��l���Ƃ�B
��3�@���F�f���̌��]������2��͑ȉ~�O���̔�������3��ɔ�Ⴗ��B
�{��́A�P�v���[�̖@���Ɋւ�����ł��B
(1) �f�������S�����x��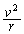 �ŁA���S����F�Ƃ��āA�f�����^���������́A
�ŁA���S����F�Ƃ��āA�f�����^���������́A 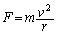 �@����@
�@����@���S���̑傫���́A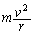 ......[��]
......[��]
�� 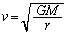 ......[��]
......[��]
(3) (2)���f�������]���x��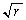 �ɔ���Ⴗ��̂ŁAr��p�{�ɂȂ�A���]���x�́A
�ɔ���Ⴗ��̂ŁAr��p�{�ɂȂ�A���]���x�́A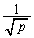 �{ ......[��]�@�ɂȂ�܂��B
�{ ......[��]�@�ɂȂ�܂��B
(4) �f�������]����T�́A
�n�������]������1�N�ł��B���]����T�� �ɔ�Ⴗ��̂ŁAr��p�{�ɂȂ�A���]���x��
�ɔ�Ⴗ��̂ŁAr��p�{�ɂȂ�A���]���x��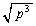 �{�ɂȂ�A�ؐ������]������
�{�ɂȂ�A�ؐ������]������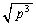 �N�ɂȂ�܂��B
�N�ɂȂ�܂��B 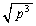 ......[��]
......[��]
(5) �P�v���[�̑�2�@�����A
��  ......[��]
......[��]
(6) �T���@���n�����o������Ƃ����͊w�I�G�l���M�[�́A�T���@��������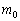 �Ƃ��āA�^���G�l���M�[
�Ƃ��āA�^���G�l���M�[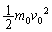 ���ʒu�G�l���M�[
���ʒu�G�l���M�[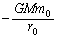 �ł��B�T���@���ؐ��̋O���ɓ��B����Ƃ����͊w�I�G�l���M�[�́A�^���G�l���M�[
�ł��B�T���@���ؐ��̋O���ɓ��B����Ƃ����͊w�I�G�l���M�[�́A�^���G�l���M�[ ���ʒu�G�l���M�[
���ʒu�G�l���M�[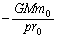 �ł��B
�ł��B 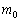 �Ŋ����āA(5)�̌��ʂ�������ƁA
�Ŋ����āA(5)�̌��ʂ�������ƁA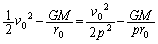 ......[��]
......[��]
(7) (6)�̌��ʂ����āA
2��������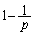 �Ŋ���ƁA
�Ŋ���ƁA �� 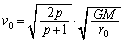 �n�������]���x��
�n�������]���x�� �Ȃ̂ŁA�n�����o������Ƃ��̒T���@�������́A�n�������]���x��
�Ȃ̂ŁA�n�����o������Ƃ��̒T���@�������́A�n�������]���x��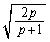 �{ ......[��]
�{ ......[��]
(8) �P�v���[�̑�3�@�����A���]������2�����������3��ɔ�Ⴗ��̂ŁA�T���@�̋O�������������n�����O�����a��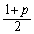 �{�ɂȂ�A�T���@�����]������
�{�ɂȂ�A�T���@�����]������ �{�ɂȂ�܂��B�n������ؐ��O���ɓ��B����܂ł����]������
�{�ɂȂ�܂��B�n������ؐ��O���ɓ��B����܂ł����]������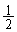 ��������������A
��������������A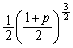 �N������܂��B
�N������܂��B 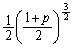 ......[��]
......[��]
(9) (4)�̌��ʂ�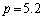 �Ƃ��邱�Ƃɂ��A
�Ƃ��邱�Ƃɂ��A 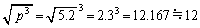 �N12 ......[��]
�N12 ......[��]
(10) (7)�̌��ʂ��A�T���@���n�����o������Ƃ��������́A
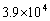 ......[��]
......[��]
(11) (8)�̌��ʂ��A
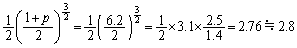 �N2.8 ......[��]
�N2.8 ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B