�k�啨��'11�N�O��[3]
�ȉ��̕��͒��� (1) ���� (9) �ɓK�Ȑ����܂��͓��������A (a) �� (b) �ɂ́A�}3�̑I��������K�Ȍ�����I�ыL���œ�����B
 ��1�@�}1�́A�g��
��1�@�}1�́A�g��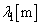 �C����
�C���� �̐��ʔg���ォ�猩�����̂ł���B���̔g�́Ay���ɕ��s�ȎR�ƒJ�̔g�ʂ������ʔg�Ƃ��ā{x�����ɐi��ł���B���̏��Ɋϑ��҂����āA�g�����Ă����B
�̐��ʔg���ォ�猩�����̂ł���B���̔g�́Ay���ɕ��s�ȎR�ƒJ�̔g�ʂ������ʔg�Ƃ��ā{x�����ɐi��ł���B���̏��Ɋϑ��҂����āA�g�����Ă����B�ϑ���A���|x�����ɑ��� �Ői��ł����B�g�̑����� (1)
�Ői��ł����B�g�̑����� (1)  �Ȃ̂ŁA�ϑ���A���g�̎R�̏ォ�玟�̎R�̏�ɗ���܂łɂ����鎞��(�ϑ���A���猩������)�� (2)
�Ȃ̂ŁA�ϑ���A���g�̎R�̏ォ�玟�̎R�̏�ɗ���܂łɂ����鎞��(�ϑ���A���猩������)�� (2)  �ƂȂ�B
�ƂȂ�B
���ɁA�ϑ���B���{x�������甽���v���Ɋp�xα (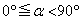 )�̌����ɑ���
)�̌����ɑ��� �Ői�Ƃ���A�ϑ���B����͔g���~�܂��Č������B���̂Ƃ��̑�����
�Ői�Ƃ���A�ϑ���B����͔g���~�܂��Č������B���̂Ƃ��̑�����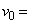 (3)
(3) 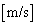 �ł���B
�ł���B
 ��2�@�}2�̂悤�ɁA���[�̈قȂ�̈�T�ƇU�����������E�Ƃ��Đڂ��Ă���B�̈�T��i��ł����g��
��2�@�}2�̂悤�ɁA���[�̈قȂ�̈�T�ƇU�����������E�Ƃ��Đڂ��Ă���B�̈�T��i��ł����g��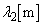 �C����
�C���� �̕��ʔg���A���E�ɓ��ˊpθ �œ��˂��A���܂����B�̈�U�ɂ�����g�̑�����
�̕��ʔg���A���E�ɓ��ˊpθ �œ��˂��A���܂����B�̈�U�ɂ�����g�̑����� �ł���Ƃ��A���̔g���� (4)
�ł���Ƃ��A���̔g���� (4)  �ƂȂ�B���܊p
�ƂȂ�B���܊p �͊W�� (5) �ɂ�茈�܂�B
�͊W�� (5) �ɂ�茈�܂�B���ɐ}3�̂悤�ɁA���E��ȕǂƂ��A�������ˊpθ �̔g�˂������B���̂Ƃ��A���˔g�͓��˔g�Ɠ��������� (a) �̌����ɐi�ށB���������āA���˔g�Ɣ��˔g�̎R�̔g�ʂ���������_A�́A (b) �̌����ɓ����B
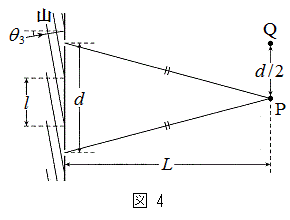 ��3�@�}4�̂悤�ɁA2�̃X���b�g��������ȕǂɁA�g��
��3�@�}4�̂悤�ɁA2�̃X���b�g��������ȕǂɁA�g��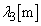 �̐��ʔg�����ˊp
�̐��ʔg�����ˊp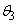 �œ��˂����B�g�͊e�X���b�g����ǂ̉E���ɋ��ʔg�Ƃ��čL�������B�e�X���b�g�̕��͋����A�ȉ��ł͕�������B�Ȃ��A2�̃X���b�g�̊Ԋu��
�œ��˂����B�g�͊e�X���b�g����ǂ̉E���ɋ��ʔg�Ƃ��čL�������B�e�X���b�g�̕��͋����A�ȉ��ł͕�������B�Ȃ��A2�̃X���b�g�̊Ԋu��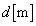 �ŁA�ǂ̗����Ŕg�̑����͓��������̂Ƃ���B
�ŁA�ǂ̗����Ŕg�̑����͓��������̂Ƃ���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��3�ł́A�ǂ̗������o�H�����l����K�v������܂��B�X���b�g��ʉ߂��Ă����ʔg���g���͕ω����Ȃ����Ƃɒ��ӂ��Ă��������B
��1(1) �g�� �C����
�C����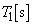 �̐��ʔg�������́A
�̐��ʔg�������́A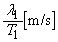 (�g�̌������Q��)
(�g�̌������Q��)  ......[��]
......[��](2) �ϑ���A���猩�����ʔg�����x�́A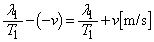 �C�����́A
�C�����́A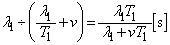
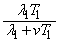 ......[��]
......[��](3) �ϑ���B�����x��x������������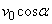 �C���ꂪ���ʔg�����x�Ɉ�v����̂ŁA
�C���ꂪ���ʔg�����x�Ɉ�v����̂ŁA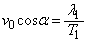
�� 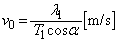
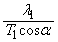 ......[��]
......[��]
��2(4) �̈�U�ɂ����镽�ʔg���g���� �Ƃ���ƁA�̈�T�Ɨ̈�U�Ƃŕ��ʔg���U�����͕ς��Ȃ��̂ŁA
�Ƃ���ƁA�̈�T�Ɨ̈�U�Ƃŕ��ʔg���U�����͕ς��Ȃ��̂ŁA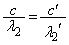
�� 
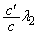 ......[��]
......[��](5) �̈�T�C�U�ł̋��ܗ������ꂼ��n�C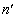 �Ƃ��āA���܂̖@�����A
�Ƃ��āA���܂̖@�����A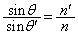
���ʔg�������͋��ܗ��ɔ���Ⴗ��̂ŁA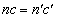
�ȏ���A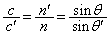
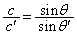 ......[��]
......[��] (a) ���˔g�Ɣ��˔g���������������E�}�ɕ`���Ă݂܂��B�E�}��蔽�˔g�̐i�ތ����́A(�N) ......[��]�@(�g�̔������Q��)
(a) ���˔g�Ɣ��˔g���������������E�}�ɕ`���Ă݂܂��B�E�}��蔽�˔g�̐i�ތ����́A(�N) ......[��]�@(�g�̔������Q��)(b) �E�}�Ԗ����_A�̐i�ތ����́A(�A) ......[��]
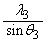 ......[��]
......[��](7) ��̃X���b�g�� �C���̃X���b�g��
�C���̃X���b�g��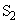 �Ƃ���ƁA
�Ƃ���ƁA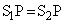 �Ȃ̂ŁA���X���b�g��ʉ߂��鐅�ʔg�̓_P�Ɏ����o�H���́A�ǂ̍����ɐ����܂��B�ǂ̍����ł��o�H��(�E�}�ԐF����)�́A�E�}���A
�Ȃ̂ŁA���X���b�g��ʉ߂��鐅�ʔg�̓_P�Ɏ����o�H���́A�ǂ̍����ɐ����܂��B�ǂ̍����ł��o�H��(�E�}�ԐF����)�́A�E�}���A
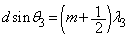 �@����@
�@����@�� 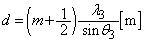
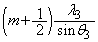 ......[��]
......[��] (8) �E�}���A���X���b�g���ʉ߂��鐅�ʔg�̕ǂ���E���ł̓_Q�Ɏ����o�H���́A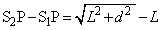
�ǂ̗������o�H���́A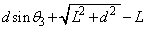
�_Q�͓_P���� �Ԗڂ̎�ߍ����_�Ȃ̂ŁA�_Q�Ŏ�ߍ��������́A
�Ԗڂ̎�ߍ����_�Ȃ̂ŁA�_Q�Ŏ�ߍ��������́A  �@����A
�@����A�A�|�@���A
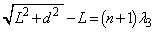 ......[��]�@����B
......[��]�@����B(9) �B���A
2�悵�āA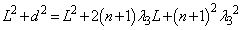
�� 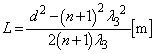
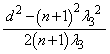 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 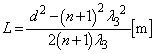
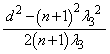 ......[��]
......[��]