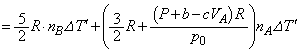��啨��'11�N�O��[3]
 ���D�ł́A�S�����k�����Ƃ���͂ɂ���ē����̈��͂��O���̈��͂�荂���Ȃ�B���̂悤�ȕ��D�ɒP���q���q���z�C��A��
���D�ł́A�S�����k�����Ƃ���͂ɂ���ē����̈��͂��O���̈��͂�荂���Ȃ�B���̂悤�ȕ��D�ɒP���q���q���z�C��A��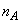 ��������A�����}�̂悤��
��������A�����}�̂悤�� �����̒P���q���q���z�C��B�̓������s�X�g���t���̃V�����_�[�ɓ��ꂽ�B���̃V�����_�[�ƃs�X�g���͊O���Ƃ̔M�̏o���肪�Ȃ��悤�Ȓf�M�ނłł��Ă���B�V�����_�[�͕��D�ɑ��ď\���傫���Ƃ���B���̃V�����_�[�ɂ̓q�[�^�[�����t�����Ă���B�s�X�g���͂Ȃ߂炩�ɓ����A���D�O���̋C��B�̈��͂͏�Ɉ���P�ł���Ƃ���B
�����̒P���q���q���z�C��B�̓������s�X�g���t���̃V�����_�[�ɓ��ꂽ�B���̃V�����_�[�ƃs�X�g���͊O���Ƃ̔M�̏o���肪�Ȃ��悤�Ȓf�M�ނłł��Ă���B�V�����_�[�͕��D�ɑ��ď\���傫���Ƃ���B���̃V�����_�[�ɂ̓q�[�^�[�����t�����Ă���B�s�X�g���͂Ȃ߂炩�ɓ����A���D�O���̋C��B�̈��͂͏�Ɉ���P�ł���Ƃ���B
�ȉ��ōl���镗�D�͔M���悭�ʂ��A���D�O���ƕ��D�����̉��x�͓����ł���B���D�͋C�̂�ʂ����Ƃ͂Ȃ��B���D������Ă���S���̎��ʁA���݁A����єM�e�ʂ͖����ł���Ƃ���B�ȉ��A�C�̒萔��R�Ƃ���B
�T�D�܂��A���D�����̋C��A�̈���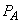 �����D�O���̋C��B�̈���P�ɂ����
�����D�O���̋C��B�̈���P�ɂ���� �Ɨ^�����镗�D�̏ꍇ���l����B������a�͐��̒萔�ł���B�C��A�ƋC��B�̉��x���Ƃ���T�̂Ƃ��A�C��A�̑̐ς�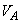 �C�C��B�̑̐ς�
�C�C��B�̑̐ς� �ł������B�ȉ��̕����� �@�@�ɓ���K�Ȏ���a�CR�CP�C
�ł������B�ȉ��̕����� �@�@�ɓ���K�Ȏ���a�CR�CP�C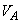 �̂����K�v�Ȃ��̂�p���ĉ��ɋL������B
�̂����K�v�Ȃ��̂�p���ĉ��ɋL������B
�C��B�̈��͂�P�ɕۂ��Ȃ���A�q�[�^�[�ŔM��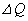 ���������B����ƁA�C��A�ƋC��B�̉��x���Ƃ��ɏオ����T����
���������B����ƁA�C��A�ƋC��B�̉��x���Ƃ��ɏオ����T����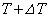 �ɂȂ����B�܂����̂Ƃ��A���D���ӂ���݁A�s�X�g���������āA�C��A�̑̐ς�
�ɂȂ����B�܂����̂Ƃ��A���D���ӂ���݁A�s�X�g���������āA�C��A�̑̐ς�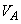 ����
���� �ɁA�C��B�̑̐ς�
�ɁA�C��B�̑̐ς�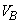 ����
����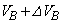 �ɂȂ����B�ω��̑O��ŋC��A�̏�ԕ��������l���邱�Ƃɂ��A
�ɂȂ����B�ω��̑O��ŋC��A�̏�ԕ��������l���邱�Ƃɂ��A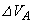 ��
�� 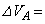 (1)
(1) 
�ƕ\�����Ƃ��ł���B
���D�̓��O�̈��͂��قȂ邽�߁A���̕ω��̊Ԃɕ��D�����̋C��A�����D�ɂ����d���ƁA���D���C��B�ɑ��Ă����d���͈قȂ�B���������āA���̍��͕��D�̃S���ɃG�l���M�[�Ƃ��Ă����킦����B�܂�A���̕ω��ŃS���ɂ����킦���Ă���G�l���M�[�� (2) 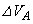 ���������������ƂɂȂ�B
���������������ƂɂȂ�B
�܂��A���̕ω��ŃV�����_�[�����̋C�̂a���s�X�g���ɑ��Ă����d��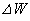 ��
�� �ł���B�C�̂̓����G�l���M�[�̑����A�C�̂��s�X�g���ɂ����d���A���D�̃S���ɂ����킦��ꂽ�G�l���M�[�̑������l�����邱�Ƃɂ��A�������M��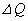 ��
�� �ł��邱�Ƃ��킩��B�������A�P���q���q���z�C�̂̒�σ�����M�� �ł���B
�ł���B
�U�D���ɁA���D�����̋C��A�̈���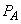 �����D�O���̋C��B�̈���P�ƋC��A�̑̐�
�����D�O���̋C��B�̈���P�ƋC��A�̑̐�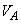 �ɂ����
�ɂ���� �Ɨ^�����镗�D�̏ꍇ���l����B������b��c�͐��̒萔�ł���B�ȉ��ł� �̏ꍇ���l����B�C��A�ƋC��B�̉��x���Ƃ���T�̂Ƃ��A�C��A�̑̐ς�
�̏ꍇ���l����B�C��A�ƋC��B�̉��x���Ƃ���T�̂Ƃ��A�C��A�̑̐ς� �C�C��B�̑̐ς�
�C�C��B�̑̐ς�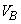 �ł������B�ȉ��̕����� �ɓ���K�Ȏ���b�Cc�CR�CP�C
�ł������B�ȉ��̕����� �ɓ���K�Ȏ���b�Cc�CR�CP�C �̂����K�v�Ȃ��̂�p���ĉ��ɋL������B
�̂����K�v�Ȃ��̂�p���ĉ��ɋL������B
�C��B�̈��͂�P�ɕۂ��Ȃ���A�q�[�^�[�Ŕ����ȔM��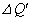 ���������B����ƁA�C��A�ƋC��B�̉��x���Ƃ��ɔ����ʂ����オ����T����
���������B����ƁA�C��A�ƋC��B�̉��x���Ƃ��ɔ����ʂ����オ����T����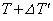 �ɂȂ�A�C��A�̑̐ς������ʂ����ω�����
�ɂȂ�A�C��A�̑̐ς������ʂ����ω�����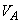 ����
���� �ɂȂ����B�ȉ��ł́A
�ɂȂ����B�ȉ��ł́A ��
�� �ɔ�ׂĔ��ɏ������̂�
�ɔ�ׂĔ��ɏ������̂�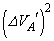 �͖����ł���Ƃ���B�ω��̑O��ŋC��A�̏�ԕ��������l���邱�Ƃɂ��A
�͖����ł���Ƃ���B�ω��̑O��ŋC��A�̏�ԕ��������l���邱�Ƃɂ��A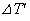 ��
�� �ƕ\�����Ƃ��ł���B�ȉ��A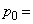 (7) �Ƃ����B
(7) �Ƃ����B
�T�̏ꍇ�Ɠ��l�ɂ��āA�C�̂̓����G�l���M�[�̑����A�C�̂��s�X�g���ɂ����d���A���D�̃S���ɂ����킦��ꂽ�G�l���M�[�̑������l�����邱�Ƃɂ��A�������M��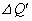 ��
��
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�V�����_�[�̒��ɂ���ɕ��D������A���D�̃S�����G�l���M�[���l������A�Ƃ�����₱�����ݒ�Ȃ̂ŁA�G�l���M�[�̂��Ƃ�̍l�@������Ȃ��Ă��܂��B
�T�D���D�����̋C�̂����� �ƕ��D�O��������P�Ƃ̊ԂɁA
�ƕ��D�O��������P�Ƃ̊ԂɁA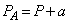 �Ƃ����W������A�Ƃ������Ƃ́A���D���\�ʐ���S�Ƃ��āA���D�����̋C�̂����D��
�Ƃ����W������A�Ƃ������Ƃ́A���D���\�ʐ���S�Ƃ��āA���D�����̋C�̂����D��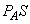 �Ƃ��������y�ڂ��A���D�O���̋C�̂����D��
�Ƃ��������y�ڂ��A���D�O���̋C�̂����D��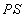 �Ƃ��������y�ڂ��̂ŁA���D�����D�����̋C�̂ɋy�ڂ�����F�Ƃ��āA�͂̂荇���̎����A
�Ƃ��������y�ڂ��̂ŁA���D�����D�����̋C�̂ɋy�ڂ�����F�Ƃ��āA�͂̂荇���̎����A �ƂȂ�A�Ƃ������Ƃł��B�܂�A���D�����D�����̋C�̂Ɉ�����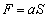 ���y�ڂ��A�Ƃ������Ƃł��B���D�\�ʂ��O�Ɍ������Ĉ�l����������
���y�ڂ��A�Ƃ������Ƃł��B���D�\�ʂ��O�Ɍ������Ĉ�l����������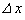 �ړ�����ƁA���D�̃S�����G�l���M�[�́A�d�͂��ʒu�G�l���M�[�Ɠ��l�ɍl���A
�ړ�����ƁA���D�̃S�����G�l���M�[�́A�d�͂��ʒu�G�l���M�[�Ɠ��l�ɍl���A �����������܂��B
������Ԃ̋C��A����ԕ������F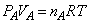 �@����@
�@����@
���M��̋C��A����ԕ������F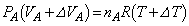 �@����A
�@����A
�A�|�@���A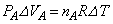 �@����B
�@����B
�� 
(1) 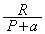 ......[��]���D�����̋C��A���C�̂ɂ����d���́A
......[��]���D�����̋C��A���C�̂ɂ����d���́A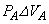 �ł��B����ŁA���D�����D�O���̋C��B�������d���́A
�ł��B����ŁA���D�����D�O���̋C��B�������d���́A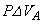 �ł��B���̍��A�܂�A���D�̃S�����~�����G�l���M�[�̑������́A
�ł��B���̍��A�܂�A���D�̃S�����~�����G�l���M�[�̑������́A (2) a ......[��]�V�����_�[�������̐��́A �����������Ă��܂��B�V�����_�[�����̋C��B���s�X�g���ɑ��Ă����d���́A
�����������Ă��܂��B�V�����_�[�����̋C��B���s�X�g���ɑ��Ă����d���́A (3) P�@(4) P ......[��]�q�[�^�[���C��B�����M���Ă���ԂɁA�C��B�������d��(3)(4)�́A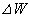
�C��A�C�C��B�������G�l���M�[�̕ω��́A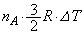 �C
�C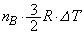
���D���~�����G�l���M�[�̑�����(2)���A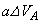
�����̑��a���������M��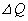 �ɂȂ�܂�(�M�͊w��1�@�����Q��)�B
�ɂȂ�܂�(�M�͊w��1�@�����Q��)�B ������Ԃ̋C��B����ԕ������F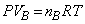 �@����C
�@����C
���M��̋C��B����ԕ������F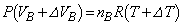 �@����D
�@����D
�D�|�C���A 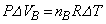 �@����E
�@����E�B�C�E��p���āA
(5) 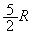 �@(6)
�@(6)  ......[��]
......[��] ���D�C��A�����D�ɂ����d���A�C��B�����D�ɂ����d���́A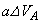 �Ƃ��āA
�Ƃ��āA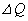 �̎��Ɍ���Ă��邱�Ƃɒ��ӂ��Ă��������B
�̎��Ɍ���Ă��邱�Ƃɒ��ӂ��Ă��������B
�U�D���x���������̐��ˑ��������̂ŁA��ԕ������������̂ɒ��ӂ��K�v�ł��B
������Ԃ̋C��A����ԕ������F �@����F
�@����F
���M��̋C��A����ԕ������F 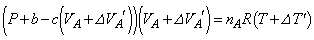 �@����G
�@����G�G�|�F���A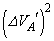 ������ƁA
������ƁA ��  �@����H(7)
�@����H(7) 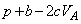 ......[��]���̏ꍇ�́A
......[��]���̏ꍇ�́A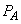 ��
�� �ɑ��ăv���b�g����ƁAp-V�}�͌X��
�ɑ��ăv���b�g����ƁAp-V�}�͌X��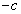 �̒����ɂȂ�܂��B
�̒����ɂȂ�܂��B
�C��A�����D�ɑ��Ă����d�� �́A
�́A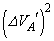 ������ƁA��`�̖ʐςƂ��āA
������ƁA��`�̖ʐςƂ��āA ���D���C��B�ɑ��Ă����d��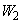 �́A
�́A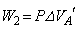
���D���~�����G�l���M�[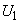 �́A
�́A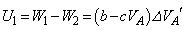
�C��B���̐��ω���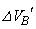 �Ƃ��āA�C��B���s�X�g���ɑ��Ă����d��
�Ƃ��āA�C��B���s�X�g���ɑ��Ă����d�� �́A
�́A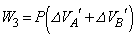
�C��A�C�C��B�������G�l���M�[�̕ω��́A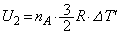 �C
�C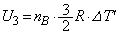
�������M��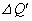 �́A�T�D�Ɠ��l�ɂ��āA
�́A�T�D�Ɠ��l�ɂ��āA (8)  �@(9)
�@(9) 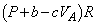 ......[��]
......[��]
���A
�� 
(10) (�A) ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B