����w2023�N�O�������������
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
[1]�@�����̉^����Փ˂ɂ��čl����B�n�_O��xy���ʂ̌��_���A����������x�����A�����������y�����Ƃ�A�����̉^����xy���ʂɌ�������̂Ƃ���B�Ȃ��A�����̑傫���͖����ł���قǏ������A�����̉�]�͍l���Ȃ����̂Ƃ��A��C��R����������B�d�͉����x�̑傫���� �ł���A���̌����͉����������ł���B
�ł���A���̌����͉����������ł���B
 �h�D����m�̏���A�𓊂������̗l�q���ώ@����B�}1�̂悤�ɁA�n�_O����pθ[rad]�̕����ɑ���
�h�D����m�̏���A�𓊂������̗l�q���ώ@����B�}1�̂悤�ɁA�n�_O����pθ[rad]�̕����ɑ��� �ŏ����𓊂����B�������A
�ŏ����𓊂����B�������A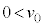 �C
�C �Ƃ���B
�Ƃ���B
��1�@����A���B����ō��_�̍������Am�C �Cθ�C
�Cθ�C �̂����K�v�Ȃ��̂�p���ĕ\���B
�̂����K�v�Ȃ��̂�p���ĕ\���B
��2�@����A�𓊂�����A���炭���ď���A�͒n��( )�ɗ��������B�����n�_�ƒn�_O�̊Ԃ̐����������Am�C
)�ɗ��������B�����n�_�ƒn�_O�̊Ԃ̐����������Am�C �Cθ�C
�Cθ�C �̂����K�v�Ȃ��̂�p���ĕ\���B
�̂����K�v�Ȃ��̂�p���ĕ\���B
��3�@�����x�̑傫�� �����ɂ����܂܂ŁA�pθ��ς��ď���A�𓊂���B�n�_O����ł������ɗ�������ꍇ�̋pθ[rad]�����߂�B
�����ɂ����܂܂ŁA�pθ��ς��ď���A�𓊂���B�n�_O����ł������ɗ�������ꍇ�̋pθ[rad]�����߂�B
��4�@������������A�͒n�ʂɏՓ˂��Ă͂˕Ԃ�A�n�ʂƂ̏Փ˂��J��Ԃ����B�n�ʂ͂Ȃ߂炩�ȖʂŁA����A�ƒn�ʂ̏Փ˂͔�e���Փ˂ł���A�����W����e�Ƃ���B����A���n�ʂ�n��ڂɏՓ˂����n�_�ƒn�_O�̊Ԃ̐����������Am�C �Cθ�C
�Cθ�C �Ce�Cn�̂����K�v�Ȃ��̂�p���ĕ\���B
�Ce�Cn�̂����K�v�Ȃ��̂�p���ĕ\���B
 �U�D�}2�̂悤�ɁA�n�_O��xy���ʂ̌��_���A����������x�����A�����������y�����Ƃ�B����M�̏���B�́A�n�_O�ŐÎ~���Ă�������m�̏���A�ɏՓ˂���B�Փ˒��O�̏���B�̑��x��
�U�D�}2�̂悤�ɁA�n�_O��xy���ʂ̌��_���A����������x�����A�����������y�����Ƃ�B����M�̏���B�́A�n�_O�ŐÎ~���Ă�������m�̏���A�ɏՓ˂���B�Փ˒��O�̏���B�̑��x�� �ł��������A�Փ˒���ɏ���A�̑��x��
�ł��������A�Փ˒���ɏ���A�̑��x��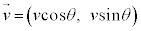 �ƂȂ�A����B�̑��x��
�ƂȂ�A����B�̑��x��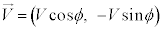 �ƂȂ����Ƃ���B�������A
�ƂȂ����Ƃ���B�������A �C
�C �C
�C �Ƃ���B�܂��A�}2�̂悤�ɁAθ[rad]��
�Ƃ���B�܂��A�}2�̂悤�ɁAθ[rad]�� ��x���̂Ȃ��p�x�ł���Aϕ[rad]��
��x���̂Ȃ��p�x�ł���Aϕ[rad]�� ��x���̂Ȃ��p�x�ł���B
��x���̂Ȃ��p�x�ł���B �C
�C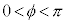 �Ƃ���B�Ȃ��A����A�Ə���B�̏Փ˂͒e���Փ˂ł���B�������A�����ƒn�ʂƂ̏Փ˂͍l���Ȃ����̂Ƃ���B
�Ƃ���B�Ȃ��A����A�Ə���B�̏Փ˂͒e���Փ˂ł���B�������A�����ƒn�ʂƂ̏Փ˂͍l���Ȃ����̂Ƃ���B
��5�@�Փ˂ɂ���Ă͂ˏグ��ꂽ����̏���A�̑���v��m�CM�C �Cθ�̂����K�v�Ȃ��̂�p���ĕ\���B
�Cθ�̂����K�v�Ȃ��̂�p���ĕ\���B
��6�@����A���͂ˏグ��ꂽ��A���炭���ď���A�� �܂ŗ��������B�����n�_�ƒn�_O�̊Ԃ̐�������L��m�CM�C
�܂ŗ��������B�����n�_�ƒn�_O�̊Ԃ̐�������L��m�CM�C �Cθ�C
�Cθ�C �̂����K�v�Ȃ��̂�p���ĕ\���B
�̂����K�v�Ȃ��̂�p���ĕ\���B
��7�@����L���ł��傫���Ȃ�ꍇ���l�������Bm�CM�C �C
�C �Cd�C
�Cd�C �̂����K�v�Ȃ��̂�p���āA�ȉ��̋ɓ���ׂ����������ɋL���B
�̂����K�v�Ȃ��̂�p���āA�ȉ��̋ɓ���ׂ����������ɋL���B  �Ƃ����ƁAL�̒l���ő�ɂȂ鎞��Z�̒l���ő�ƂȂ�B
�Ƃ����ƁAL�̒l���ő�ɂȂ鎞��Z�̒l���ő�ƂȂ�B (
( )�Ƃ����A�\���ɏ�����d�̕ω��ł���
)�Ƃ����A�\���ɏ�����d�̕ω��ł��� �ɑ��āAZ�̕ω�
�ɑ��āAZ�̕ω� �́A
�́A (
( )�̍�������ƁA
)�̍�������ƁA �Ə�����BZ�̒l���ő�ƂȂ�ꍇ�Ad�̕ω�
�Ə�����BZ�̒l���ő�ƂȂ�ꍇ�Ad�̕ω� �ɑ���
�ɑ��� �ƂȂ�̂ŁAL�̒l���ő�ɂȂ�
�ƂȂ�̂ŁAL�̒l���ő�ɂȂ� �̒l��
�̒l�� �ƂȂ�B
�ƂȂ�B
�V�D�U�ł́A����A�Ə���B�����킹��2���̂̏d�SG�̈ʒu�́A���ԂƂƂ��Ɉړ�����B�U�̏���A�Ə���B�̏Փ˂��A�d�SG�ƂƂ��Ɉړ�����ϑ���P����ώ@����B�Ȃ��A����A�Ə���B�̎��ʂ͂��ꂼ��m��M�ł���B
��8�@�ϑ���P���猩������A�Ə���B�̉^�������߂����Bm�CM�C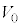 �C
�C �̂����K�v�Ȃ��̂�p���āA�ȉ��̋ɓ���ׂ����������ɋL���B
�̂����K�v�Ȃ��̂�p���āA�ȉ��̋ɓ���ׂ����������ɋL���B �U�̍��W�n�ł́A����A�Ə���B�̍��W�����ꂼ�� ��
�� �Ƃ���A2���̂̏d�SG�̍��W��
�Ƃ���A2���̂̏d�SG�̍��W�� �ƕ\�����B�Փ˒��O�ɏ���A�͒n�_O�ɐÎ~���Ă���A����B�͐�������(x���̐��̌���)�ɑ��� �������Ă����̂ŁA��������
�������Ă����̂ŁA�������� �̊Ԃɂ�����d�SG�̍��W�̕ω��ʂ�
�̊Ԃɂ�����d�SG�̍��W�̕ω��ʂ� �ƕ\�����B�䂦�ɁA�d�SG�̑��x��
�ƕ\�����B�䂦�ɁA�d�SG�̑��x�� �ƂȂ�B����āA�Փ˒��O�ɂ����āA�d�SG�ƂƂ��Ɉړ�����ϑ���P���猩������A�̑��x��
�ƂȂ�B����āA�Փ˒��O�ɂ����āA�d�SG�ƂƂ��Ɉړ�����ϑ���P���猩������A�̑��x�� �ł���A����B�̑��x��
�ł���A����B�̑��x�� �ƂȂ�B
�ƂȂ�B
��9�@�Փ˒���ɁA�ϑ���P���猩������A�̑��x�� �ƂȂ�A����B�̑��x��
�ƂȂ�A����B�̑��x�� �ƂȂ����B
�ƂȂ����B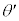 [rad]��
[rad]�� ��x���̂Ȃ��p�x�ł���A
��x���̂Ȃ��p�x�ł���A [rad]��
[rad]�� ��x���̂Ȃ��p�x�ł���B�������A
��x���̂Ȃ��p�x�ł���B�������A �C
�C �Ƃ���B�Փ˒���ɂ����鏬��A�̑���
�Ƃ���B�Փ˒���ɂ����鏬��A�̑��� �C����B�̑���
�C����B�̑��� �C
�C ��m�CM�C
��m�CM�C �̂����K�v�Ȃ��̂�p���ĕ\���B
�̂����K�v�Ȃ��̂�p���ĕ\���B
��10�@����B�̎���M������A�̎���m���傫���ꍇ�A�U�̍��W�n�Ō�������B�̊p�xϕ�ɂ͏��������Bm�CM�C �̂����K�v�Ȃ��̂�p���āA
�̂����K�v�Ȃ��̂�p���āA �̏���l��\���B
�̏���l��\���B
[��]
 [2]�@�}1�̂悤�ɁA�^�ɔ��a�����ꂼ��
[2]�@�}1�̂悤�ɁA�^�ɔ��a�����ꂼ�� �����
����� �̈ꊪ���̉~�`�R�C��A�����B������ʓ��ɒ��S�����낦�Ēu����Ă���A�R�C��A�ɂ͕��s�R���f���T�[�ƋN�d��V�̒����d�����A�R�C��B�ɂ͒�R�lr�̒�R���A���ꂼ��ڑ�����Ă���B�R���f���T�[�́A�ӂ̒�����a�Cb�̒����`�̋ɔ�A����ыɔ�B�ō\������A�ɔԂ̋�����d�ł���A�ɔԂ͐^��ł���B�����ŁAd��a�Cb�ɔ�ׂď\���������A�ɔ[���̓d�E�̌��ʂ͖����ł���Ƃ���B�܂��A�R�C��A�����B�̓d�C��R�������ł���Ƃ���B�����ł́A�R���f���T�[�A�����d���A��R�̃T�C�Y�̓R�C���̔��a�ɔ�ׂď\���������A�R�C���͉~�`�R�C���Ƃ݂Ȃ��Ď��E���v�Z���Ă悢�B�ȉ��ł́A�^��̗U�d������ѓ����������ꂼ��
�̈ꊪ���̉~�`�R�C��A�����B������ʓ��ɒ��S�����낦�Ēu����Ă���A�R�C��A�ɂ͕��s�R���f���T�[�ƋN�d��V�̒����d�����A�R�C��B�ɂ͒�R�lr�̒�R���A���ꂼ��ڑ�����Ă���B�R���f���T�[�́A�ӂ̒�����a�Cb�̒����`�̋ɔ�A����ыɔ�B�ō\������A�ɔԂ̋�����d�ł���A�ɔԂ͐^��ł���B�����ŁAd��a�Cb�ɔ�ׂď\���������A�ɔ[���̓d�E�̌��ʂ͖����ł���Ƃ���B�܂��A�R�C��A�����B�̓d�C��R�������ł���Ƃ���B�����ł́A�R���f���T�[�A�����d���A��R�̃T�C�Y�̓R�C���̔��a�ɔ�ׂď\���������A�R�C���͉~�`�R�C���Ƃ݂Ȃ��Ď��E���v�Z���Ă悢�B�ȉ��ł́A�^��̗U�d������ѓ����������ꂼ�� �����
����� �Ƃ���B
�Ƃ���B
 �T�D���܁A�}1���̃R���f���T�[�̋ɔ��ɁA�}2�̂悤�ɁA�ӂ̒�����a�Cb�Cd�̒����̗̂U�d�̂�}������B�U�d�̂̑}������}2�Ɏ����悤��s�Ƃ���B�U�d�̂�
�T�D���܁A�}1���̃R���f���T�[�̋ɔ��ɁA�}2�̂悤�ɁA�ӂ̒�����a�Cb�Cd�̒����̗̂U�d�̂�}������B�U�d�̂̑}������}2�Ɏ����悤��s�Ƃ���B�U�d�̂� �̒n�_����A�����x��0�C�����x�̑傫����p (
�̒n�_����A�����x��0�C�����x�̑傫����p ( )�œ������x�^��������ƃR�C��B�ɓd�������ꂽ�B�U�d�̂̑}������
)�œ������x�^��������ƃR�C��B�ɓd�������ꂽ�B�U�d�̂̑}������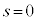 �̂Ƃ��̎�����
�̂Ƃ��̎�����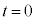 �Ƃ���B�ȉ��̖�ɓ�����B�����ŁA�R�C��A�̎��ȗU���ɂ��t�N�d�͂͏����������ł���Ƃ��A�܂��A�R�C��B�ɗ����d������鎥�E���キ�����ł���Ƃ���B�Ȃ��A�U�d�̂̔�U�d����
�Ƃ���B�ȉ��̖�ɓ�����B�����ŁA�R�C��A�̎��ȗU���ɂ��t�N�d�͂͏����������ł���Ƃ��A�܂��A�R�C��B�ɗ����d������鎥�E���キ�����ł���Ƃ���B�Ȃ��A�U�d�̂̔�U�d���� �ł���A�U�d�̒[���̓d�E�̌��ʂ͖����ł���Ƃ���B
�ł���A�U�d�̒[���̓d�E�̌��ʂ͖����ł���Ƃ���B
��1�@�U�d�̂̑}������s ( )�̂Ƃ��ɃR���f���T�[�ɒ~�����Ă���d�C�ʂ�a�Cb�Cd�Cs�C
)�̂Ƃ��ɃR���f���T�[�ɒ~�����Ă���d�C�ʂ�a�Cb�Cd�Cs�C �C
�C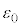 �CV�̂����K�v�Ȃ��̂�p���ĕ\���B
�CV�̂����K�v�Ȃ��̂�p���ĕ\���B
��2�@���܁A����t ����������� �̊ԂɁA�U�d�̂̑}������s����
�̊ԂɁA�U�d�̂̑}������s���� �ɕω������Ƌߎ����āA���̊ԂɃR�C��A�ɗ����d���̑傫��
�ɕω������Ƌߎ����āA���̊ԂɃR�C��A�ɗ����d���̑傫��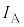 ��
��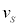 �Ca�Cb�Cd�C
�Ca�Cb�Cd�C �C
�C �CV�̂����K�v�Ȃ��̂�p���ĕ\���B�����ŁA
�CV�̂����K�v�Ȃ��̂�p���ĕ\���B�����ŁA (
( )�͑}������s�̂Ƃ��̗U�d�̂̑��x�ł���B�܂��A���̓d���̌�����}1���̋L��(i)�܂���(ii)�ɂ�莦���B
)�͑}������s�̂Ƃ��̗U�d�̂̑��x�ł���B�܂��A���̓d���̌�����}1���̋L��(i)�܂���(ii)�ɂ�莦���B
��3�@����t �ɂ����ēd�� ���R�C���̒��S�ɂ��鎥�E�̋�����
���R�C���̒��S�ɂ��鎥�E�̋����� �C
�C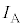 �C
�C �̂����K�v�Ȃ��̂�p���ĕ\���B�܂����̌����́A�}1�ɂ�����(�A)���ʕ\���痠�̌����A���邢��(�C)���ʗ�����\�̌����A�̂����ǂ���ł��邩�B(�A)�܂���(�C)�̋L���Ŏ����B
�̂����K�v�Ȃ��̂�p���ĕ\���B�܂����̌����́A�}1�ɂ�����(�A)���ʕ\���痠�̌����A���邢��(�C)���ʗ�����\�̌����A�̂����ǂ���ł��邩�B(�A)�܂���(�C)�̋L���Ŏ����B
��4�@����t ����������� �̊ԂɗU�d�̂̑��x��
�̊ԂɗU�d�̂̑��x�� ����
���� �ɂȂ����Ƃ��āA���̊ԂɃR�C��B�ɗ����d��
�ɂȂ����Ƃ��āA���̊ԂɃR�C��B�ɗ����d�� �̑傫����r�C
�̑傫����r�C �C
�C �Ca�Cb�Cd�Cp�C
�Ca�Cb�Cd�Cp�C �C
�C �C
�C �CV�̂����K�v�Ȃ��̂�p���ĕ\���B�܂��A���̓d���̌�����}1���̋L��(iii)�܂���(iv)�ɂ�莦���B�������A�R�C��B�̔��a
�CV�̂����K�v�Ȃ��̂�p���ĕ\���B�܂��A���̓d���̌�����}1���̋L��(iii)�܂���(iv)�ɂ�莦���B�������A�R�C��B�̔��a �̓R�C��A�̔��a
�̓R�C��A�̔��a �ɔ�ׂď\���������A�R�C��B�̓����̎��E�͈�l�Œ��S�̒l�ɓ������Ƃ���B
�ɔ�ׂď\���������A�R�C��B�̓����̎��E�͈�l�Œ��S�̒l�ɓ������Ƃ���B ��5�@�U�d�̂�}�����n�߂�����ɃR�C��B�ɗ����d���̑傫���� �Ƃ��āA�U�d�̂̑}������0����a�܂ŕω�����Ԃɒ�Rr�ŏ�����G�l���M�[��r�C
�Ƃ��āA�U�d�̂̑}������0����a�܂ŕω�����Ԃɒ�Rr�ŏ�����G�l���M�[��r�C �Ca�Cp�̂����K�v�Ȃ��̂�p���ĕ\���B
�Ca�Cp�̂����K�v�Ȃ��̂�p���ĕ\���B
 ��6�@���̂Ƃ��́A���̃R���f���T�[�̓d�C�e�ʂ��A�}4�̂悤�ɋɔ�n�̔�����Ԃɓ��������Ăł����A�d�C�e�ʂ�
��6�@���̂Ƃ��́A���̃R���f���T�[�̓d�C�e�ʂ��A�}4�̂悤�ɋɔ�n�̔�����Ԃɓ��������Ăł����A�d�C�e�ʂ� �̔������s�R���f���T�[�����������d�C�e�ʂł���ƍl���悤�B������k��1����n�܂ł̐����ł���B���̕��͂̋ɓ����ׂ����������ɋL���B
�̔������s�R���f���T�[�����������d�C�e�ʂł���ƍl���悤�B������k��1����n�܂ł̐����ł���B���̕��͂̋ɓ����ׂ����������ɋL���B
 �ɔ�AB�Ԃ̋����͐}5�Ɏ���x��1�����ŕ\�����B���_�����琔����k�Ԗڂ̔������s�R���f���T�[�̋ɔԂ̋�����
�ɔ�AB�Ԃ̋����͐}5�Ɏ���x��1�����ŕ\�����B���_�����琔����k�Ԗڂ̔������s�R���f���T�[�̋ɔԂ̋����� �ɂ�����ɔ�AB�Ԃ̋����ł���Ƃ���A���̋ɔԂ̋�����d�C
�ɂ�����ɔ�AB�Ԃ̋����ł���Ƃ���A���̋ɔԂ̋�����d�C �Cn�Ck��p����
�Cn�Ck��p���� �ƕ\�����B���������āA�������s�R���f���T�[�̍����e�ʂ�a�Cb�Cd�C
�ƕ\�����B���������āA�������s�R���f���T�[�̍����e�ʂ�a�Cb�Cd�C �Cn�Ck�C
�Cn�Ck�C ��p����
��p���� �ƕ\�����B���܁A������n���\���傫���Ƃ��̔������s�R���f���T�[�̍����e�ʂ́A���̋ߎ���K�p�����a�Cb�Cd�C
�ƕ\�����B���܁A������n���\���傫���Ƃ��̔������s�R���f���T�[�̍����e�ʂ́A���̋ߎ���K�p�����a�Cb�Cd�C �C
�C ��p����
��p���� �ƕ\�����Bn���\���傫���A����δ��1�ɔ�ׂď\���������ꍇ�F
�ƕ\�����Bn���\���傫���A����δ��1�ɔ�ׂď\���������ꍇ�F
��7�@�}1�̂悤�ɒ����d���ƃR���f���T�[�͂Ȃ����Ă���B�ʒux�ɂ�����ɔ�A��̒P�ʖʐς�����̓d�C�ʂ�x�Ca�Cd�C �C
�C �CV�̂����K�v�Ȃ��̂�p���ĕ\���B
�CV�̂����K�v�Ȃ��̂�p���ĕ\���B
 ��8�@������x�C�c�����ɔ�A��̒P�ʖʐς�����̓d�C��σ�Ƃ��āA�ό`�O�ƕό`���σ�̕��z���O���t�ɕ`���Ƃǂ̂悤�ɂȂ邩�B�}6����(��)����(��)�̒�����ł��K�Ȃ��̂�I�ׁB�������A�}����
��8�@������x�C�c�����ɔ�A��̒P�ʖʐς�����̓d�C��σ�Ƃ��āA�ό`�O�ƕό`���σ�̕��z���O���t�ɕ`���Ƃǂ̂悤�ɂȂ邩�B�}6����(��)����(��)�̒�����ł��K�Ȃ��̂�I�ׁB�������A�}���� �͋ɔ��L����O�̋ɔ�A��̒P�ʖʐς�����̓d�C�ʂł���B
�͋ɔ��L����O�̋ɔ�A��̒P�ʖʐς�����̓d�C�ʂł���B
��9�@�� �ƕ�
�ƕ� ���㉺�ɓ������L����ہA���ꂼ��̕ӂ̏����x��0�C�����x�̑傫����
���㉺�ɓ������L����ہA���ꂼ��̕ӂ̏����x��0�C�����x�̑傫���� �ň��Ƃ���B�ɔ��L���n�߂�����ɃR�C��B�ɗ����d���̑傫����r�C
�ň��Ƃ���B�ɔ��L���n�߂�����ɃR�C��B�ɗ����d���̑傫����r�C �C
�C �Ca�Cb�Cd�Cq�C
�Ca�Cb�Cd�Cq�C �C
�C �CV�̂����K�v�Ȃ��̂�p���ĕ\���B
�CV�̂����K�v�Ȃ��̂�p���ĕ\���B
[��]
[3]�@
�ȉ���A��B�̗����̖��ɉ���B�Ȃ�A��B�͓Ɨ��������e�̖��ł���B
 A�D�}1�̂悤�ɔM��ʂ��Ȃ������łł���2�̕��D���Ȃ����킹���C��������B����̕��D�ɂ͒P���q���q���z�C�̂ł���C��A�C��������̕��D�ɂ͓q���q���z�C�̂ł���C��B�������Ă���B���D�͂��ꂼ�ꖧ����Ă��ċC��A�CB�͍������Ȃ��B���D�̍ގ��͗͂킸�ɐL�яk�݂ł���̂ŁA���D���̋C�̂̈��͂͑�C���Ə�Ɉ�v���Ă���Ƃ���B2�̕��D�̐ڑ����ɂ͉��u����ł���q�[�^�[�A��p��A�f�M������B�f�M���J���Ă���Ƃ��́A�C��A�CB�݂͌��ɔM�������ł���B�f�M���J������ԂŃq�[�^�[���p���p����ƁA���C�̂̉��x����v�������܂܉��x���������ƕω������邱�Ƃ��ł���B�C�̂��\�����镨���̂����A�C��A�CB�ȊO�̕����̎��ʁA�̐ρA�M�e�ʂ͍l�����Ȃ��Ă悢�B���x�͂��ׂĐ�Ή��x�Ƃ���B
A�D�}1�̂悤�ɔM��ʂ��Ȃ������łł���2�̕��D���Ȃ����킹���C��������B����̕��D�ɂ͒P���q���q���z�C�̂ł���C��A�C��������̕��D�ɂ͓q���q���z�C�̂ł���C��B�������Ă���B���D�͂��ꂼ�ꖧ����Ă��ċC��A�CB�͍������Ȃ��B���D�̍ގ��͗͂킸�ɐL�яk�݂ł���̂ŁA���D���̋C�̂̈��͂͑�C���Ə�Ɉ�v���Ă���Ƃ���B2�̕��D�̐ڑ����ɂ͉��u����ł���q�[�^�[�A��p��A�f�M������B�f�M���J���Ă���Ƃ��́A�C��A�CB�݂͌��ɔM�������ł���B�f�M���J������ԂŃq�[�^�[���p���p����ƁA���C�̂̉��x����v�������܂܉��x���������ƕω������邱�Ƃ��ł���B�C�̂��\�����镨���̂����A�C��A�CB�ȊO�̕����̎��ʁA�̐ρA�M�e�ʂ͍l�����Ȃ��Ă悢�B���x�͂��ׂĐ�Ή��x�Ƃ���B
�C��A�CB�̕����ʁA�������ʁA��σ�����M�A�舳������M��\1�Ɏ����BR�͋C�̒萔�A�������ʂ�1����������̎��ʂł���B��C�̓������ʂ�M�̗��z�C�̂ł���Ƃ���B�n�ʂ���̍��x�������Ȃ�قǑ�C�̈��͂▧�x�͏������Ȃ邪�A�C��A�CB�̏�Ԃ��v�Z����ꍇ�ɂ͋C���̒��S���x�ɑΉ������C�����C�̂̈��͂Ƃ��ėp���A�e���D���ň��͂▧�x����l�ł���Ƃ��Ă悢�B���̉e���͂Ȃ����̂Ƃ���B�n��̑�C�̈��͂� �C���x��
�C���x�� �ł������B�d�͉����x�̑傫����
�ł������B�d�͉����x�̑傫���� �Ƃ��A���x�ɂ�炸���Ƃ���B
�Ƃ��A���x�ɂ�炸���Ƃ���B
�T�D�ŏ��A�}1�̂悤�ɋC���͒n�ʂɒ��n���Ă���A�C��A�CB�̉��x�͑�C�̉��x �Ɠ����ł������B�f�M���J������ԂŃq�[�^�[��p���ċC��A�CB���ɉ��߂��Ƃ���A���x��
�Ɠ����ł������B�f�M���J������ԂŃq�[�^�[��p���ċC��A�CB���ɉ��߂��Ƃ���A���x�� �ɂȂ����Ƃ��ɋC�����n�ʂ𗣂�ĕ����n�߂��B�ȉ��̖��n�CM�C
�ɂȂ����Ƃ��ɋC�����n�ʂ𗣂�ĕ����n�߂��B�ȉ��̖��n�CM�C �C
�C �C
�C �C
�C �CR�C
�CR�C �̂����K�v�Ȃ��̂�p���ē�����B
�̂����K�v�Ȃ��̂�p���ē�����B
��1�@�C���������n�߂��Ƃ��A�C���ɓ����Ă���P�ʑ̐ς�����̕��͂̑傫�������߂�B
��2�@ �����߂�B
�����߂�B
��3�@���x�� ����
���� �ɂȂ�܂łɃq�[�^�[���C��A�CB�ɗ^�����M�ʂ̍��v�����߂�B
�ɂȂ�܂łɃq�[�^�[���C��A�CB�ɗ^�����M�ʂ̍��v�����߂�B
�U�D���ɁA�C�����㏸���Ă����Ȃ��悤�ɂЂ��Œn�ʂɌŒ肵���B�C��A�CB�̉��x�� �ƂȂ�܂ʼn��߂����_�Ńq�[�^�[���~���A�f�M����ċC��A�CB�̔M�������Ւf�����B�C������Ђ����O�����Ƃ���A�C���͏��ɂ������Əオ���Ă����A���鍂�x�ŐÎ~�����B�Î~�����C���̒��S���x�̑�C���͒n��̑�C����a�{�ł������Ba�̑傫���͈̔͂�
�ƂȂ�܂ʼn��߂����_�Ńq�[�^�[���~���A�f�M����ċC��A�CB�̔M�������Ւf�����B�C������Ђ����O�����Ƃ���A�C���͏��ɂ������Əオ���Ă����A���鍂�x�ŐÎ~�����B�Î~�����C���̒��S���x�̑�C���͒n��̑�C����a�{�ł������Ba�̑傫���͈̔͂� �ł���B���ŐÎ~�����Ƃ��̋C��A�̉��x��
�ł���B���ŐÎ~�����Ƃ��̋C��A�̉��x�� �C�C��B�̉��x��
�C�C��B�̉��x�� �Ƃ���B
�Ƃ���B
��4�@ ��
�� ��n�CM�C
��n�CM�C �C
�C �Ca�C
�Ca�C �C
�C �CR�C
�CR�C �̂����K�v�Ȃ��̂�p���ĕ\���B�Ȃ��A�C��A�CB�̈��͕ω��͏\���������ł���̂ŁA���z�C�̂̒f�M�c���ߒ��ł͈���(p)�Ƒ̐�(V)���u
�̂����K�v�Ȃ��̂�p���ĕ\���B�Ȃ��A�C��A�CB�̈��͕ω��͏\���������ł���̂ŁA���z�C�̂̒f�M�c���ߒ��ł͈���(p)�Ƒ̐�(V)���u �v�̊W�������Ƃ��g�p���Ă悢�B������γ�͒舳������M���σ�����M�Ŋ������l�ł���B
�v�̊W�������Ƃ��g�p���Ă悢�B������γ�͒舳������M���σ�����M�Ŋ������l�ł���B
 B�D��l�ŗ��ꂪ�Ȃ���C���𑬂�V�œ`��鉹���l����B���͑�C���ɐÎ~������������A�����I�ɋ��ʔg�Ƃ��Ĕ�������B�ϑ��҂Ɖ����̑傫���͖����ł���Ƃ��A���̓`�����͉����ɂ�藐����Ȃ��Ƃ���B�}2�̓_S�ʼn������U����
B�D��l�ŗ��ꂪ�Ȃ���C���𑬂�V�œ`��鉹���l����B���͑�C���ɐÎ~������������A�����I�ɋ��ʔg�Ƃ��Ĕ�������B�ϑ��҂Ɖ����̑傫���͖����ł���Ƃ��A���̓`�����͉����ɂ�藐����Ȃ��Ƃ���B�}2�̓_S�ʼn������U���� �̉����Ă���B���̉��̐U�������A�ϑ��҂��_S���狗��d�������ꂽ�_O�𒆐S�Ƃ��锼�a
�̉����Ă���B���̉��̐U�������A�ϑ��҂��_S���狗��d�������ꂽ�_O�𒆐S�Ƃ��锼�a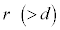 �̉~�O����ŁA�}2�̂悤�ɔ����v���Ɋp���xω�œ����~�^�����Ȃ���ϑ�����B���̂Ƃ��ϑ��҂��ϑ����鉹�̐U�����́A�ϑ��҂Ɖ��������Ԓ��������̑��x������p���ċ��߂邱�Ƃ��ł���B�ϑ��҂̈ʒu��_P�C
�̉~�O����ŁA�}2�̂悤�ɔ����v���Ɋp���xω�œ����~�^�����Ȃ���ϑ�����B���̂Ƃ��ϑ��҂��ϑ����鉹�̐U�����́A�ϑ��҂Ɖ��������Ԓ��������̑��x������p���ċ��߂邱�Ƃ��ł���B�ϑ��҂̈ʒu��_P�C �̊p�x��θ�Ƃ���B�ϑ��҂��A����
�̊p�x��θ�Ƃ���B�ϑ��҂��A����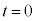 ��
�� �̓_��ʉ߂��Ă���A���̉~���������Ԃɂ��Ĉȉ��̖�ɓ�����B��������̉���
�̓_��ʉ߂��Ă���A���̉~���������Ԃɂ��Ĉȉ��̖�ɓ�����B��������̉��� �Ŋ��Ɋϑ��҂ɓ͂��Ă���Ƃ���B�ϑ��҂̑����͉������\���x���Ƃ���B�Ȃ��A�ϑ��҂̉����x�͏\���������Ƃ��A���̐U�������v�Z����ۂ́A���̎��_�ł̊ϑ��҂̑��x�����Ƃ��Čv�Z����B�܂��A�p�x�̒P�ʂ̓��W�A���Ƃ���B
�Ŋ��Ɋϑ��҂ɓ͂��Ă���Ƃ���B�ϑ��҂̑����͉������\���x���Ƃ���B�Ȃ��A�ϑ��҂̉����x�͏\���������Ƃ��A���̐U�������v�Z����ۂ́A���̎��_�ł̊ϑ��҂̑��x�����Ƃ��Čv�Z����B�܂��A�p�x�̒P�ʂ̓��W�A���Ƃ���B
��6�@�ϑ��҂� ��
�� �̐U�������ϑ������̂��A�ӂ�����
�̐U�������ϑ������̂��A�ӂ����� �̐U�������ϑ�����ŏ��̎������AV�C
�̐U�������ϑ�����ŏ��̎������AV�C �Cd�Cω�Cr�̂����K�v�Ȃ��̂�p���ĕ\���B
�Cd�Cω�Cr�̂����K�v�Ȃ��̂�p���ĕ\���B
��7�@�ϑ��҂��ϑ����鉹�̐U���������߂�ɂ́A�ϑ��҂̑��x��SP����(S����P�Ɍ�������)�̐��� ���K�v�ł���B�p�xθ�̈ʒu�ɂ�����ϑ��҂�
���K�v�ł���B�p�xθ�̈ʒu�ɂ�����ϑ��҂� ��V�C
��V�C �Cd�Cω�Cr�Cθ�̂����K�v�Ȃ��̂�p���ĕ\���B
�Cd�Cω�Cr�Cθ�̂����K�v�Ȃ��̂�p���ĕ\���B �q���g�F �͊ϑ��҂̑��x�x�N�g��
�͊ϑ��҂̑��x�x�N�g�� �ƁASP������\���x�N�g��
�ƁASP������\���x�N�g�� �Ƃ��̑傫��
�Ƃ��̑傫�� ��p���āA
��p���āA �̂悤�ɓ��ς��g���ċ��߂邱�Ƃ��ł���B
�̂悤�ɓ��ς��g���ċ��߂邱�Ƃ��ł���B
��8�@��7�� �̑傫�����v�Z����ƁA
�̑傫�����v�Z����ƁA �ƂȂ�θ�ɂ����čő�ƂȂ邱�Ƃ��킩�����B���̂��Ƃ�p���A���̕��͂�
�ƂȂ�θ�ɂ����čő�ƂȂ邱�Ƃ��킩�����B���̂��Ƃ�p���A���̕��͂� ��
�� �ɓ���ׂ��������AV�C
�ɓ���ׂ��������AV�C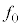 �Cd�Cω�Cr�̂����K�v�Ȃ��̂�p���ĉ��ɋL���B
�Cd�Cω�Cr�̂����K�v�Ȃ��̂�p���ĉ��ɋL���B �ϑ��҂��ŏ��̐U�������ϑ������Ƃ��� �̑傫���́A
�̑傫���́A �ƕ\�����B���������āA�ϑ��҂��ϑ�����ŏ��̐U������
�ƕ\�����B���������āA�ϑ��҂��ϑ�����ŏ��̐U������ �ƕ\�����B
�ƕ\�����B
��9�@�ϑ��҂��ϑ�����ő�̐U�������AV�C �Cd�Cω�Cr�̂����K�v�Ȃ��̂�p���ĕ\���B
�Cd�Cω�Cr�̂����K�v�Ȃ��̂�p���ĕ\���B
��10�@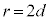 �ł���Ƃ��A�ϑ��҂��ŏ��̐U�������ϑ����Ă��玟�ɍő�̐U�������ϑ�����܂łɂ����鎞�Ԃ��AV�C
�ł���Ƃ��A�ϑ��҂��ŏ��̐U�������ϑ����Ă��玟�ɍő�̐U�������ϑ�����܂łɂ����鎞�Ԃ��AV�C �Cd�Cω�̂����K�v�Ȃ��̂�p���ĕ\���B
�Cd�Cω�̂����K�v�Ȃ��̂�p���ĕ\���B [��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 
 �ƂȂ�B����āA�Փ˒��O�ɂ����āA�d�SG�ƂƂ��Ɉړ�����ϑ���P���猩������A�̑��x��
�ƂȂ�B����āA�Փ˒��O�ɂ����āA�d�SG�ƂƂ��Ɉړ�����ϑ���P���猩������A�̑��x�� �ƕ\�����B���܁A������n���\���傫���Ƃ��̔������s�R���f���T�[�̍����e�ʂ́A���̋ߎ���K�p�����a�Cb�Cd�C
�ƕ\�����B���܁A������n���\���傫���Ƃ��̔������s�R���f���T�[�̍����e�ʂ́A���̋ߎ���K�p�����a�Cb�Cd�C
 �̂悤�ɓ��ς��g���ċ��߂邱�Ƃ��ł���B
�̂悤�ɓ��ς��g���ċ��߂邱�Ƃ��ł���B