��啨��'23�N�O��[3]
�ȉ���A��B�̗����̖��ɉ���B�Ȃ�A��B�͓Ɨ��������e�̖��ł���B
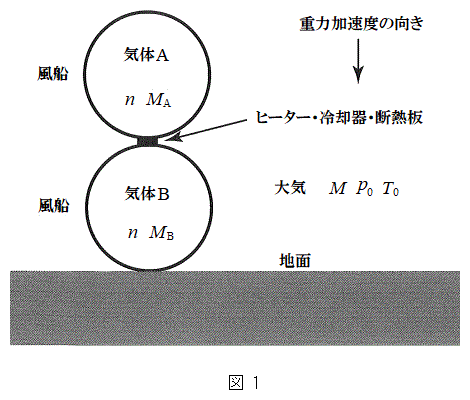 A�D�}1�̂悤�ɔM��ʂ��Ȃ������łł���2�̕��D���Ȃ����킹���C��������B����̕��D�ɂ͒P���q���q���z�C�̂ł���C��A�C��������̕��D�ɂ͓q���q���z�C�̂ł���C��B�������Ă���B���D�͂��ꂼ�ꖧ����Ă��ċC��A�CB�͍������Ȃ��B���D�̍ގ��͗͂킸�ɐL�яk�݂ł���̂ŁA���D���̋C�̂̈��͂͑�C���Ə�Ɉ�v���Ă���Ƃ���B2�̕��D�̐ڑ����ɂ͉��u����ł���q�[�^�[�A��p��A�f�M������B�f�M���J���Ă���Ƃ��́A�C��A�CB�݂͌��ɔM�������ł���B�f�M���J������ԂŃq�[�^�[���p���p����ƁA���C�̂̉��x����v�������܂܉��x���������ƕω������邱�Ƃ��ł���B�C�̂��\�����镨���̂����A�C��A�CB�ȊO�̕����̎��ʁA�̐ρA�M�e�ʂ͍l�����Ȃ��Ă悢�B���x�͂��ׂĐ�Ή��x�Ƃ���B
A�D�}1�̂悤�ɔM��ʂ��Ȃ������łł���2�̕��D���Ȃ����킹���C��������B����̕��D�ɂ͒P���q���q���z�C�̂ł���C��A�C��������̕��D�ɂ͓q���q���z�C�̂ł���C��B�������Ă���B���D�͂��ꂼ�ꖧ����Ă��ċC��A�CB�͍������Ȃ��B���D�̍ގ��͗͂킸�ɐL�яk�݂ł���̂ŁA���D���̋C�̂̈��͂͑�C���Ə�Ɉ�v���Ă���Ƃ���B2�̕��D�̐ڑ����ɂ͉��u����ł���q�[�^�[�A��p��A�f�M������B�f�M���J���Ă���Ƃ��́A�C��A�CB�݂͌��ɔM�������ł���B�f�M���J������ԂŃq�[�^�[���p���p����ƁA���C�̂̉��x����v�������܂܉��x���������ƕω������邱�Ƃ��ł���B�C�̂��\�����镨���̂����A�C��A�CB�ȊO�̕����̎��ʁA�̐ρA�M�e�ʂ͍l�����Ȃ��Ă悢�B���x�͂��ׂĐ�Ή��x�Ƃ���B
�C��A�CB�̕����ʁA�������ʁA��σ�����M�A�舳������M��\1�Ɏ����BR�͋C�̒萔�A�������ʂ�1����������̎��ʂł���B��C�̓������ʂ�M�̗��z�C�̂ł���Ƃ���B�n�ʂ���̍��x�������Ȃ�قǑ�C�̈��͂▧�x�͏������Ȃ邪�A�C��A�CB�̏�Ԃ��v�Z����ꍇ�ɂ͋C���̒��S���x�ɑΉ������C�����C�̂̈��͂Ƃ��ėp���A�e���D���ň��͂▧�x����l�ł���Ƃ��Ă悢�B���̉e���͂Ȃ����̂Ƃ���B�n��̑�C�̈��͂� �C���x��
�C���x�� �ł������B�d�͉����x�̑傫����
�ł������B�d�͉����x�̑傫���� �Ƃ��A���x�ɂ�炸���Ƃ���B
�Ƃ��A���x�ɂ�炸���Ƃ���B
�T�D�ŏ��A�}1�̂悤�ɋC���͒n�ʂɒ��n���Ă���A�C��A�CB�̉��x�͑�C�̉��x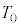 �Ɠ����ł������B�f�M���J������ԂŃq�[�^�[��p���ċC��A�CB���ɉ��߂��Ƃ���A���x��
�Ɠ����ł������B�f�M���J������ԂŃq�[�^�[��p���ċC��A�CB���ɉ��߂��Ƃ���A���x��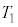 �ɂȂ����Ƃ��ɋC�����n�ʂ𗣂�ĕ����n�߂��B�ȉ��̖��n�CM�C
�ɂȂ����Ƃ��ɋC�����n�ʂ𗣂�ĕ����n�߂��B�ȉ��̖��n�CM�C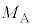 �C
�C �C
�C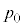 �C
�C �CR�C
�CR�C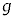 �̂����K�v�Ȃ��̂�p���ē�����B
�̂����K�v�Ȃ��̂�p���ē�����B
��1�@�C���������n�߂��Ƃ��A�C���ɓ����Ă���P�ʑ̐ς�����̕��͂̑傫�������߂�B
��2�@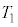 �����߂�B
�����߂�B
��3�@���x�� ����
���� �ɂȂ�܂łɃq�[�^�[���C��A�CB�ɗ^�����M�ʂ̍��v�����߂�B
�ɂȂ�܂łɃq�[�^�[���C��A�CB�ɗ^�����M�ʂ̍��v�����߂�B
�U�D���ɁA�C�����㏸���Ă����Ȃ��悤�ɂЂ��Œn�ʂɌŒ肵���B�C��A�CB�̉��x��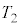 �ƂȂ�܂ʼn��߂����_�Ńq�[�^�[���~���A�f�M����ċC��A�CB�̔M�������Ւf�����B�C������Ђ����O�����Ƃ���A�C���͏��ɂ������Əオ���Ă����A���鍂�x�ŐÎ~�����B�Î~�����C���̒��S���x�̑�C���͒n��̑�C����a�{�ł������Ba�̑傫���͈̔͂�
�ƂȂ�܂ʼn��߂����_�Ńq�[�^�[���~���A�f�M����ċC��A�CB�̔M�������Ւf�����B�C������Ђ����O�����Ƃ���A�C���͏��ɂ������Əオ���Ă����A���鍂�x�ŐÎ~�����B�Î~�����C���̒��S���x�̑�C���͒n��̑�C����a�{�ł������Ba�̑傫���͈̔͂� �ł���B���ŐÎ~�����Ƃ��̋C��A�̉��x��
�ł���B���ŐÎ~�����Ƃ��̋C��A�̉��x�� �C�C��B�̉��x��
�C�C��B�̉��x�� �Ƃ���B
�Ƃ���B
��4�@ ��
��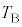 ��n�CM�C
��n�CM�C �C
�C �Ca�C
�Ca�C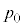 �C
�C �CR�C
�CR�C �̂����K�v�Ȃ��̂�p���ĕ\���B�Ȃ��A�C��A�CB�̈��͕ω��͏\���������ł���̂ŁA���z�C�̂̒f�M�c���ߒ��ł͈���(p)�Ƒ̐�(V)���u
�̂����K�v�Ȃ��̂�p���ĕ\���B�Ȃ��A�C��A�CB�̈��͕ω��͏\���������ł���̂ŁA���z�C�̂̒f�M�c���ߒ��ł͈���(p)�Ƒ̐�(V)���u �v�̊W�������Ƃ��g�p���Ă悢�B������γ�͒舳������M���σ�����M�Ŋ������l�ł���B
�v�̊W�������Ƃ��g�p���Ă悢�B������γ�͒舳������M���σ�����M�Ŋ������l�ł���B
 B�D��l�ŗ��ꂪ�Ȃ���C���𑬂�V�œ`��鉹���l����B���͑�C���ɐÎ~������������A�����I�ɋ��ʔg�Ƃ��Ĕ�������B�ϑ��҂Ɖ����̑傫���͖����ł���Ƃ��A���̓`�����͉����ɂ�藐����Ȃ��Ƃ���B�}2�̓_S�ʼn������U����
B�D��l�ŗ��ꂪ�Ȃ���C���𑬂�V�œ`��鉹���l����B���͑�C���ɐÎ~������������A�����I�ɋ��ʔg�Ƃ��Ĕ�������B�ϑ��҂Ɖ����̑傫���͖����ł���Ƃ��A���̓`�����͉����ɂ�藐����Ȃ��Ƃ���B�}2�̓_S�ʼn������U����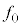 �̉����Ă���B���̉��̐U�������A�ϑ��҂��_S���狗��d�������ꂽ�_O�𒆐S�Ƃ��锼�a
�̉����Ă���B���̉��̐U�������A�ϑ��҂��_S���狗��d�������ꂽ�_O�𒆐S�Ƃ��锼�a �̉~�O����ŁA�}2�̂悤�ɔ����v���Ɋp���xω�œ����~�^�����Ȃ���ϑ�����B���̂Ƃ��ϑ��҂��ϑ����鉹�̐U�����́A�ϑ��҂Ɖ��������Ԓ��������̑��x������p���ċ��߂邱�Ƃ��ł���B�ϑ��҂̈ʒu��_P�C
�̉~�O����ŁA�}2�̂悤�ɔ����v���Ɋp���xω�œ����~�^�����Ȃ���ϑ�����B���̂Ƃ��ϑ��҂��ϑ����鉹�̐U�����́A�ϑ��҂Ɖ��������Ԓ��������̑��x������p���ċ��߂邱�Ƃ��ł���B�ϑ��҂̈ʒu��_P�C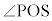 �̊p�x��θ�Ƃ���B�ϑ��҂��A����
�̊p�x��θ�Ƃ���B�ϑ��҂��A���� ��
��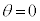 �̓_��ʉ߂��Ă���A���̉~���������Ԃɂ��Ĉȉ��̖�ɓ�����B��������̉���
�̓_��ʉ߂��Ă���A���̉~���������Ԃɂ��Ĉȉ��̖�ɓ�����B��������̉��� �Ŋ��Ɋϑ��҂ɓ͂��Ă���Ƃ���B�ϑ��҂̑����͉������\���x���Ƃ���B�Ȃ��A�ϑ��҂̉����x�͏\���������Ƃ��A���̐U�������v�Z����ۂ́A���̎��_�ł̊ϑ��҂̑��x�����Ƃ��Čv�Z����B�܂��A�p�x�̒P�ʂ̓��W�A���Ƃ���B
�Ŋ��Ɋϑ��҂ɓ͂��Ă���Ƃ���B�ϑ��҂̑����͉������\���x���Ƃ���B�Ȃ��A�ϑ��҂̉����x�͏\���������Ƃ��A���̐U�������v�Z����ۂ́A���̎��_�ł̊ϑ��҂̑��x�����Ƃ��Čv�Z����B�܂��A�p�x�̒P�ʂ̓��W�A���Ƃ���B
��6�@�ϑ��҂�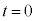 ��
�� �̐U�������ϑ������̂��A�ӂ�����
�̐U�������ϑ������̂��A�ӂ�����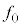 �̐U�������ϑ�����ŏ��̎������AV�C
�̐U�������ϑ�����ŏ��̎������AV�C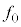 �Cd�Cω�Cr�̂����K�v�Ȃ��̂�p���ĕ\���B
�Cd�Cω�Cr�̂����K�v�Ȃ��̂�p���ĕ\���B
��7�@�ϑ��҂��ϑ����鉹�̐U���������߂�ɂ́A�ϑ��҂̑��x��SP����(S����P�Ɍ�������)�̐��� ���K�v�ł���B�p�xθ�̈ʒu�ɂ�����ϑ��҂�
���K�v�ł���B�p�xθ�̈ʒu�ɂ�����ϑ��҂�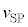 ��V�C
��V�C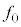 �Cd�Cω�Cr�Cθ�̂����K�v�Ȃ��̂�p���ĕ\���B
�Cd�Cω�Cr�Cθ�̂����K�v�Ȃ��̂�p���ĕ\���B �q���g�F �͊ϑ��҂̑��x�x�N�g��
�͊ϑ��҂̑��x�x�N�g��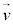 �ƁASP������\���x�N�g��
�ƁASP������\���x�N�g��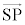 �Ƃ��̑傫��
�Ƃ��̑傫�� ��p���āA
��p���āA �̂悤�ɓ��ς��g���ċ��߂邱�Ƃ��ł���B
�̂悤�ɓ��ς��g���ċ��߂邱�Ƃ��ł���B
��8�@��7�� �̑傫�����v�Z����ƁA
�̑傫�����v�Z����ƁA �ƂȂ�θ�ɂ����čő�ƂȂ邱�Ƃ��킩�����B���̂��Ƃ�p���A���̕��͂�
�ƂȂ�θ�ɂ����čő�ƂȂ邱�Ƃ��킩�����B���̂��Ƃ�p���A���̕��͂� ��
�� �ɓ���ׂ��������AV�C
�ɓ���ׂ��������AV�C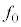 �Cd�Cω�Cr�̂����K�v�Ȃ��̂�p���ĉ��ɋL���B
�Cd�Cω�Cr�̂����K�v�Ȃ��̂�p���ĉ��ɋL���B �ϑ��҂��ŏ��̐U�������ϑ������Ƃ���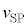 �̑傫���́A
�̑傫���́A �ƕ\�����B���������āA�ϑ��҂��ϑ�����ŏ��̐U������
�ƕ\�����B���������āA�ϑ��҂��ϑ�����ŏ��̐U������ �ƕ\�����B
�ƕ\�����B
��9�@�ϑ��҂��ϑ�����ő�̐U�������AV�C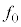 �Cd�Cω�Cr�̂����K�v�Ȃ��̂�p���ĕ\���B
�Cd�Cω�Cr�̂����K�v�Ȃ��̂�p���ĕ\���B
��10�@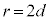 �ł���Ƃ��A�ϑ��҂��ŏ��̐U�������ϑ����Ă��玟�ɍő�̐U�������ϑ�����܂łɂ����鎞�Ԃ��AV�C
�ł���Ƃ��A�ϑ��҂��ŏ��̐U�������ϑ����Ă��玟�ɍő�̐U�������ϑ�����܂łɂ����鎞�Ԃ��AV�C �Cd�Cω�̂����K�v�Ȃ��̂�p���ĕ\���B
�Cd�Cω�̂����K�v�Ȃ��̂�p���ĕ\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@A��B���ڐV�������ł��BA��5�́A���͂������A�ƍŏ�����C�Â��Ȃ��Ɠ��ł�(�Ȃ��A�M�C�����Q�Ƃ��Ă�������)�BB�͖�蕶�̃q���g�ʂ�ɍl����Ή��Ƃ��Ȃ�܂��B
A�D
��1�@�C���̑̐ς�V�C�n�ʕt�߂̑�C�̖��x��ρ�Ƃ��āA�̐�V�̒��ɓ����C�̎��ʂ� �ł��邱�Ƃ���A�A���L���f�X�̌������A�C���ɓ��������́A
�ł��邱�Ƃ���A�A���L���f�X�̌������A�C���ɓ��������́A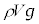 �ł��B�P�ʑ̐ϓ�����̕��͂̑傫���́A
�ł��B�P�ʑ̐ϓ�����̕��͂̑傫���́A  �@����@
�@����@��C���̐�V���߂�Ƃ��̑�C�̃�������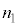 �Ƃ���ƁA�n�ʕt�߂̑�C����ԕ������́A
�Ƃ���ƁA�n�ʕt�߂̑�C����ԕ������́A  ��
�� 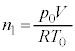
��C�̃������ʁA�܂�A1����������̎��ʂ�M�ł��邱�Ƃ���A�n�ʕt�߂̑�C�̖��x�́A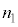 �����̑�C�̎��ʂ�̐ςŊ����āA
�����̑�C�̎��ʂ�̐ςŊ����āA 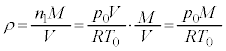 �@����A
�@����A����āA�@���A�P�ʑ̐ϓ�����̕��͂̑傫���́A ......[��]
......[��]
��2�@���x�� �ƂȂ�C�����㏸���n�߂��Ƃ��A���DA�̑̐ς�
�ƂȂ�C�����㏸���n�߂��Ƃ��A���DA�̑̐ς�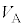 �C���DB�̑̐ς�
�C���DB�̑̐ς�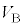 �Ƃ���ƁA
�Ƃ���ƁA ���DA���̋C�̂���ԕ������́A �@����B
�@����B
���DB���̋C�̂���ԕ������́A �@����C
�@����C
�B�C�C���A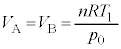 �@����D�@(�f�M���J���Ă����Ԃł́A�C��A�ƋC��B�̑̐ς͓������Ȃ�܂�)��C���̐�
�@����D�@(�f�M���J���Ă����Ԃł́A�C��A�ƋC��B�̑̐ς͓������Ȃ�܂�)��C���̐�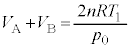 ���߂�Ƃ��̑�C�̃�������
���߂�Ƃ��̑�C�̃������� �Ƃ���ƁA�n�ʕt�߂ł́A��C�̉��x��
�Ƃ���ƁA�n�ʕt�߂ł́A��C�̉��x�� �ł����āA��C�̏�ԕ������́A
�ł����āA��C�̏�ԕ������́A 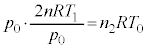 ��
�� 
�C���ɓ������͂̑傫����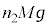 �ł��B����ŁA�C�����̋C��A�C�C��B�ɓ����d�̘͂a�́A
�ł��B����ŁA�C�����̋C��A�C�C��B�ɓ����d�̘͂a�́A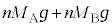 �ł���A���҂��荇�����A
�ł���A���҂��荇�����A
��3�@���x�� ����
���� �ɂȂ�܂ł̕��D���̋C�̂̕ω��́A���͂�
�ɂȂ�܂ł̕��D���̋C�̂̕ω��́A���͂� �ň��Ȃ̂��舳�ω��ł��B�q�[�^�[���C��A�CB�ɗ^�����M�ʂ̍��v�́A�舳������M�̎����A
�ň��Ȃ̂��舳�ω��ł��B�q�[�^�[���C��A�CB�ɗ^�����M�ʂ̍��v�́A�舳������M�̎����A 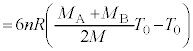
 ......[��]
......[��]
��4�@���x�� �̂Ƃ��ɂ��āA�f�M���J���Ă���̂ŇD�Ɠ��l�ɕ��DA�C���DB�̑̐ς͓����������
�̂Ƃ��ɂ��āA�f�M���J���Ă���̂ŇD�Ɠ��l�ɕ��DA�C���DB�̑̐ς͓����������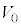 �Ƃ����ƁA���D���̋C�̂̏�ԕ������́A
�Ƃ����ƁA���D���̋C�̂̏�ԕ������́A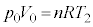 �@����E
�@����E ���ɏオ�����Ƃ��A���D���̋C�̂̈��͂�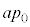 �ł��B���̂Ƃ��A���DA�̑̐ς�
�ł��B���̂Ƃ��A���DA�̑̐ς�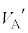 �C�C��A�̉��x��
�C�C��A�̉��x�� �C���DB�̑̐ς�
�C���DB�̑̐ς�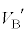 �C�C��B�̉��x��
�C�C��B�̉��x��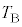 �Ƃ����(�C��A�CB�̔M�������Ւf���Ă���̂ŁA
�Ƃ����(�C��A�CB�̔M�������Ւf���Ă���̂ŁA �C
�C �ł�)�A
�ł�)�A
���DA���̋C�̂̏�ԕ������́A �@����F
�@����F
���DB���̋C�̂̏�ԕ������́A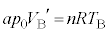 �@����G
�@����G
�F���E���A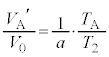 �@����H
�@����H
�G���E���A �@����I
�@����I
��蕶�ɏ�����Ă����|�A�b�\���̊W��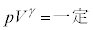 ���A�C��A�̔�M��(�舳������M���σ�����M�Ŋ������l)��
���A�C��A�̔�M��(�舳������M���σ�����M�Ŋ������l)�� �C�C��B�̔�M���
�C�C��B�̔�M��� �Ƃ��āA
�Ƃ��āA
���DA���̋C�̂ɂ��āA
���@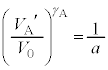 �C
�C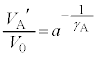
���DB���̋C�̂ɂ��āA
���@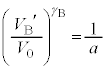 �C
�C
�H�C�I���A
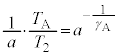 ��
��  ......[��]
......[��]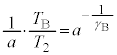 ��
��  ......[��]
......[��]
��5�@�܂��A���Œf�M���J���ċC��A�ƋC��B�̉��x����v�����Ƃ��̉��x��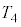 �Ƃ���ƁA�f�M���J���O��œ����G�l���M�[���ۑ�����邱�Ƃ���A
�Ƃ���ƁA�f�M���J���O��œ����G�l���M�[���ۑ�����邱�Ƃ���A 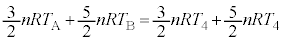 ��
�� 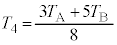
�ƂȂ��āA �����߂邱�Ƃ͂ł���̂ł����A
�����߂邱�Ƃ͂ł���̂ł����A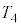 ����
����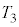 �܂ŗ�₷(
�܂ŗ�₷(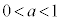 �Ȃ̂�
�Ȃ̂� �ł���
�ł���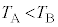 �C����
�C���� �ł�)�ߒ����ǂ������ω��Ȃ̂����킩��܂���B��₵�Ă��邩��f�M�ω��ł͂Ȃ��A���x���ω�����̂œ����ω��ł��Ȃ��A���x���ω�����̂ň��͂��ω����舳�ω��ł��Ȃ��A�̐ς��ω�����̂Œ�ϕω��ł�����܂���B�܂�A�ω���ǂ��Ă��A
�ł�)�ߒ����ǂ������ω��Ȃ̂����킩��܂���B��₵�Ă��邩��f�M�ω��ł͂Ȃ��A���x���ω�����̂œ����ω��ł��Ȃ��A���x���ω�����̂ň��͂��ω����舳�ω��ł��Ȃ��A�̐ς��ω�����̂Œ�ϕω��ł�����܂���B�܂�A�ω���ǂ��Ă��A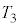 �����߂邱�Ƃ͂ł��܂���B�����ŁA�ω���ɂ��āA�l���Ă݂܂��B
�����߂邱�Ƃ͂ł��܂���B�����ŁA�ω���ɂ��āA�l���Ă݂܂��B
���x�� �ɂ����Ƃ��A�f�M���J���O�Ɠ������S���x�ɖ߂����A�Ƃ������Ƃ́A���̂Ƃ��̋C�����̈��͂�
�ɂ����Ƃ��A�f�M���J���O�Ɠ������S���x�ɖ߂����A�Ƃ������Ƃ́A���̂Ƃ��̋C�����̈��͂�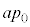 ���Ƃ������Ƃł��B�f�M���J���Ă���̂ŇD�Ɠ��l�ɂ��ĕ��DA�C���DB�̑̐ς�
���Ƃ������Ƃł��B�f�M���J���Ă���̂ŇD�Ɠ��l�ɂ��ĕ��DA�C���DB�̑̐ς� �Ƃ����ƁA���D���̋C�̂̏�ԕ������́A
�Ƃ����ƁA���D���̋C�̂̏�ԕ������́A 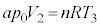 �@����J
�@����J�J���E���A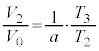 �@����K
�@����K
�����ŁA�C���ɓ������͂̑傫�������߂邽�߂ɁA��C���C������ ��������Ƃ��āA��ԕ������𗧂Ă����Ă��A��C�̕��̉��x(
��������Ƃ��āA��ԕ������𗧂Ă����Ă��A��C�̕��̉��x( �ł͂���܂���)��������Ȃ��̂ŁA
�ł͂���܂���)��������Ȃ��̂ŁA �����߂��܂���B�܂��A����C�̃������ʂ��^�����Ă��܂���B�܂�A�C�̂̏���͕��͂̑傫�������߂��Ȃ��̂ł��B�ł����A�C���ɓ����������d�����荇���̎��͗��Ă邱�Ƃ��ł��܂��B
�����߂��܂���B�܂��A����C�̃������ʂ��^�����Ă��܂���B�܂�A�C�̂̏���͕��͂̑傫�������߂��Ȃ��̂ł��B�ł����A�C���ɓ����������d�����荇���̎��͗��Ă邱�Ƃ��ł��܂��B
���̍��x�̑�C�̖��x�� �Ƃ���ƁA���͂̑傫���͗����D�̑̐�
�Ƃ���ƁA���͂̑傫���͗����D�̑̐�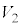 ��p����
��p����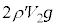 �Ə����܂��B�C�����̋C�̂ɓ����d�͂́A��2�ōl�����悤��
�Ə����܂��B�C�����̋C�̂ɓ����d�͂́A��2�ōl�����悤�� �ł��B�͂̂荇�����A
�ł��B�͂̂荇�����A  �@����L
�@����L���x��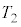 �̂Ƃ����A�C���͉��x
�̂Ƃ����A�C���͉��x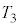 �̂Ƃ��Ɠ������x�Ȃ̂ŁA��C�̖��x�͂�͂�
�̂Ƃ��Ɠ������x�Ȃ̂ŁA��C�̖��x�͂�͂�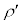 �C���DA�CB�̑̐ς�
�C���DA�CB�̑̐ς� �C
�C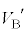 �Ȃ̂ŁA���͂̑傫����
�Ȃ̂ŁA���͂̑傫����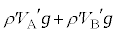 �Ə����܂��B�C�����̋C�̂ɓ����d�͕͂ς�炸
�Ə����܂��B�C�����̋C�̂ɓ����d�͕͂ς�炸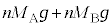 �ł��B�͂̂荇�����A
�ł��B�͂̂荇�����A 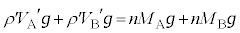 �@����M
�@����M�L�C�M���A (�܂�A�͂��荇���Ă���A�Î~���邢�͓����x�^���̏ł́A���͓͂����l)
(�܂�A�͂��荇���Ă���A�Î~���邢�͓����x�^���̏ł́A���͓͂����l) ��  �@����N
�@����N �K�C�H�C�I���A
 ��
�� 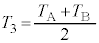 ......[��]
......[��]
B�D
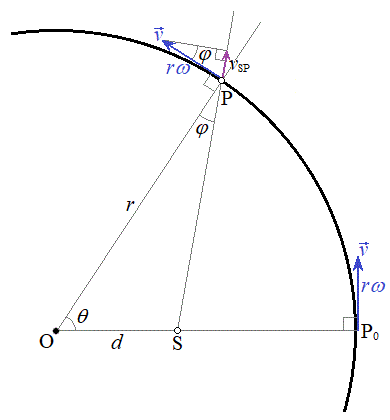 ��6�@�ϑ���P��
��6�@�ϑ���P�� ��
�� �̐U�������ϑ�����̂́A�ϑ��҂��E�}��
�̐U�������ϑ�����̂́A�ϑ��҂��E�}��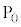 �ɂ��āA�ϑ���P�̑��x
�ɂ��āA�ϑ���P�̑��x ��
��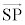 ����������0������ł��B�܂�A�ϑ���P�̑��x��
����������0������ł��B�܂�A�ϑ���P�̑��x��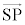 ����������0�ɂȂ�Ƃ��ɂ́A�ϑ���P��
����������0�ɂȂ�Ƃ��ɂ́A�ϑ���P��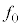 �̐U�������ϑ����邱�ƂɂȂ�܂��B
�̐U�������ϑ����邱�ƂɂȂ�܂��B �̎��ɁA�ϑ���P�̑��x��
�̎��ɁA�ϑ���P�̑��x�� ����������0�ɂȂ�̂́A�ϑ���P��
����������0�ɂȂ�̂́A�ϑ���P�� ����[�Ƃ��钼�a�̑��[�ɗ����Ƃ��ł��B���̂Ƃ�
����[�Ƃ��钼�a�̑��[�ɗ����Ƃ��ł��B���̂Ƃ� �ł����A�����ɗ���܂ł̎��Ԃ͊ϑ��҂̓����~�^���̊p���x��ω�Ȃ̂ŁA
�ł����A�����ɗ���܂ł̎��Ԃ͊ϑ��҂̓����~�^���̊p���x��ω�Ȃ̂ŁA ......[��]
......[��]
��7�@��蕶���q���g�������𗘗p����ƁA�E�}�ŁAO�����_�Ƃ�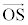 ������x���A����Ɛ����ȕ�����y���Ƃ�����W�n���Ƃ�ƁA
������x���A����Ɛ����ȕ�����y���Ƃ�����W�n���Ƃ�ƁA  ���A
���A����āA ......[��]
......[��]
��8�@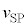 �͉���S���牓��������������Ȃ̂ŁA�ϑ������U����f �́A�h�b�v���[�����̌������A
�͉���S���牓��������������Ȃ̂ŁA�ϑ������U����f �́A�h�b�v���[�����̌������A 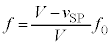 �@����O�@(��7�̌��ʂɂ����
�@����O�@(��7�̌��ʂɂ����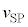 ���l����A
���l����A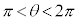 �ɂ����Ă��A
�ɂ����Ă��A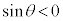 �Ȃ̂ł��̎��͐������܂�)
�Ȃ̂ł��̎��͐������܂�)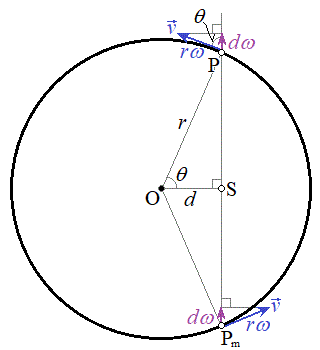 �O�����A
�O�����A ���ő�ɂȂ�Ƃ��ϑ��҂��ϑ�����U�������ŏ��ŁA
���ő�ɂȂ�Ƃ��ϑ��҂��ϑ�����U�������ŏ��ŁA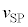 ���ŏ��̂Ƃ��ϑ��҂��ϑ�����U�������ő�ɂȂ�܂��B
���ŏ��̂Ƃ��ϑ��҂��ϑ�����U�������ő�ɂȂ�܂��B
��蕶���A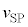 ��
��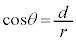 �̂Ƃ��ɍő�ɂȂ�܂����A��7�̌��ʂ�
�̂Ƃ��ɍő�ɂȂ�܂����A��7�̌��ʂ�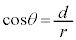 �Ƃ���ƁA
�Ƃ���ƁA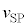 �̍ő�l�́A
�̍ő�l�́A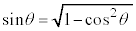 ���A
���A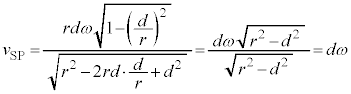 �@����P�@(�E�}�ł́A���̂Ƃ�
�@����P�@(�E�}�ł́A���̂Ƃ�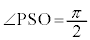 �ł����āA
�ł����āA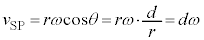 �ƂȂ��Ă��܂�)
�ƂȂ��Ă��܂�)����āA�ϑ��҂��ŏ��̐U�������ϑ������Ƃ���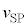 �̑傫���́A
�̑傫���́A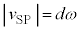 ......(a)�ϑ��҂��ϑ�����ŏ��̐U����
......(a)�ϑ��҂��ϑ�����ŏ��̐U����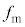 �́A�O����
�́A�O����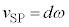 �Ƃ��āA
�Ƃ��āA 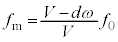 ......(b)
......(b)���D��蕶�̃q���g��������ƁA��7�� ��
�� �Ƃ���
�Ƃ���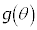 ��θ�Ŕ������āA
��θ�Ŕ������āA  �Ƃ���ƁA
�Ƃ���ƁA �Ȃ̂�(
�Ȃ̂�(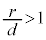 �Ȃ̂�
�Ȃ̂�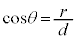 �ɂ͂Ȃ蓾�܂���)�A
�ɂ͂Ȃ蓾�܂���)�A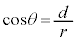
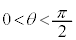 �ɂ�����
�ɂ�����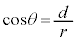 ����θ��
�����
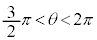 �ɂ�����
�ɂ�����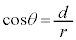 ����θ��
�����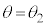
�Ƃ���ƁA�����\�͈ȉ��̂悤�ɂȂ�܂��B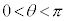 �ɂ�����θ�����
�ɂ�����θ�����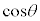 �����A�ɒ��ӂ��Ă��������B
�����A�ɒ��ӂ��Ă��������B| θ | 0 | �@ |  | �@ | π | �@ | 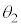 | �@ | 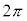 |
 | 1 | �@ | 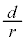 | �@ | 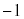 | �@ |  | �@ | 1 |
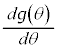 | �{ | �{ | 0 | �| | �| | �| | 0 | �{ | �{ |
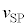 | 0 |  |  |  | 0 |  |  |  | 0 |
�����\���A �̂Ƃ�
�̂Ƃ� �͍ő�l
�͍ő�l ���Ƃ�A
���Ƃ�A �̂Ƃ�
�̂Ƃ�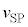 �͍ŏ��l
�͍ŏ��l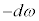 ���Ƃ邱�Ƃ�������܂��B�ł����A������Ŗ�蕶���Ƀq���g�Ƃ��ė^�����Ă��邱�Ƃ��m�F����悤�Ȃ��Ƃ��n�߂Ă��܂��ƁA���i�͓���Ȃ邩���m��܂���B
���Ƃ邱�Ƃ�������܂��B�ł����A������Ŗ�蕶���Ƀq���g�Ƃ��ė^�����Ă��邱�Ƃ��m�F����悤�Ȃ��Ƃ��n�߂Ă��܂��ƁA���i�͓���Ȃ邩���m��܂���B
��9�@�ϑ������U�������ő�ƂȂ�̂́A�O��� ���ŏ��̂Ƃ��ł����A����͊ϑ��҂��E��}��
���ŏ��̂Ƃ��ł����A����͊ϑ��҂��E��}��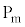 �ɗ����Ƃ��ŁA���̂Ƃ�
�ɗ����Ƃ��ŁA���̂Ƃ�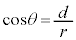 �C
�C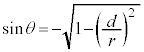 �ƂȂ�A�P�Ɠ��l�ɁA
�ƂȂ�A�P�Ɠ��l�ɁA (
( �͉�������Ƃ����Ȃ̂ŁA���ɂȂ�Ƃ������Ƃ́A
�͉�������Ƃ����Ȃ̂ŁA���ɂȂ�Ƃ������Ƃ́A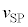 �͉����ɋ߂Â������ł�)�ƂȂ�܂��B�ϑ��҂��ϑ�����ő�̐U����
�͉����ɋ߂Â������ł�)�ƂȂ�܂��B�ϑ��҂��ϑ�����ő�̐U���� �́A�h�b�v���[�����̌����O�ɂ�����
�́A�h�b�v���[�����̌����O�ɂ�����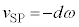 �Ƃ��邱�Ƃɂ��A
�Ƃ��邱�Ƃɂ��A 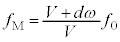 ......[��]
......[��]
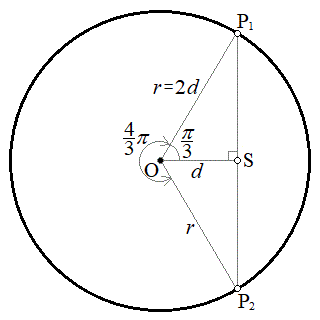 ��10�@
��10�@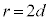 �̂Ƃ�
�̂Ƃ�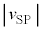 ���ő�Ƃ���
���ő�Ƃ���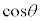 �́A��8���
�́A��8���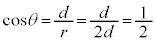 �ł��B���̂Ƃ��A
�ł��B���̂Ƃ��A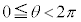 �ɂ����ẮA
�ɂ����ẮA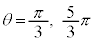 �ł��B��8�E��9�ł̌������A
�ł��B��8�E��9�ł̌������A �̂Ƃ��̊ϑ��҂̈ʒu�͉E�}��
�̂Ƃ��̊ϑ��҂̈ʒu�͉E�}��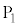 �ŁA�����Ŋϑ������U�������ŏ��ɂȂ�܂��B
�ŁA�����Ŋϑ������U�������ŏ��ɂȂ�܂��B �̂Ƃ��̊ϑ��҂̈ʒu�͉E�}��
�̂Ƃ��̊ϑ��҂̈ʒu�͉E�}��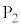 �ŁA�����Ŋϑ������U�������ő�ɂȂ�܂��B����āA�ϑ��҂��ŏ��̐U�������ϑ����Ă��玟�ɍő�̐U�������ϑ�����܂łɂ����鎞�Ԃ́A�ϑ��҂̓����~�^���̊p���x��ω�ł��邱�Ƃ���A
�ŁA�����Ŋϑ������U�������ő�ɂȂ�܂��B����āA�ϑ��҂��ŏ��̐U�������ϑ����Ă��玟�ɍő�̐U�������ϑ�����܂łɂ����鎞�Ԃ́A�ϑ��҂̓����~�^���̊p���x��ω�ł��邱�Ƃ���A ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  �̂悤�ɓ��ς��g���ċ��߂邱�Ƃ��ł���B
�̂悤�ɓ��ς��g���ċ��߂邱�Ƃ��ł���B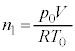
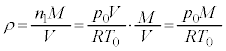 �@����A
�@����A ......[��]
......[��]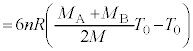
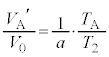 �@����H
�@����H �@����I
�@����I �C�C��B�̔�M���
�C�C��B�̔�M��� �Ƃ��āA
�Ƃ��āA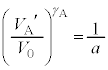 �C
�C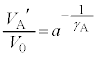
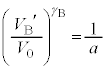 �C
�C
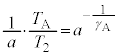
 �@����K
�@����K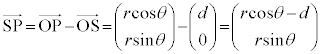
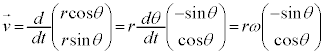

 ......[��]
......[��]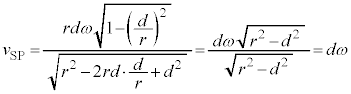 �@����P�@(�E�}�ł́A���̂Ƃ�
�@����P�@(�E�}�ł́A���̂Ƃ�
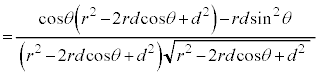
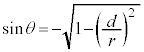 �ƂȂ�A�P�Ɠ��l�ɁA
�ƂȂ�A�P�Ɠ��l�ɁA ......[��]
......[��]