�f�M�ω��@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�C�̂��O���ƔM�̂��Ƃ�����邱�ƂȂ��s����ԕω����f�M�ω��ƌ����B
���z�C���̒f�M�ω��ɂ����āA�C�̂̂����d��W�́A�����G�l���M�[�̕ω�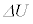 �̕�����ς������̂ɓ������A�C�̂̃�������n�C���������M��
�̕�����ς������̂ɓ������A�C�̂̃�������n�C���������M��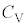 �Ƃ��āA
�Ƃ��āA
�܂��A�f�M�ω��ɂ����āA����p�C�̐�V�̊Ԃɂ́A
�Ƃ����W������B���̎����|�A�b�\���̊W���ƌ����Bγ �́A��M��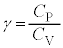 �ł���B
�ł���B
�f�M�ω���p�|V�}�́A�����Ȑ������X�����}�ɂȂ�B
�f�M�ω��ɂ����ẮA�C�̂��z�������M��0�ŁA�C�̂̂����d����W�C�����G�l���M�[�̕ω���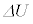 �Ƃ��āA�M�͊w���@�����A
�Ƃ��āA�M�͊w���@�����A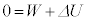
�� 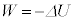
�f�M�ω��̊ԂɁA��Ή��x��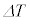 �ω������Ƃ���ƁA���z�C�̂̃�������n�C��σ�����M��
�ω������Ƃ���ƁA���z�C�̂̃�������n�C��σ�����M��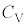 �Ƃ��āA
�Ƃ��āA
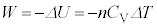 �@����@
�@����@
�@���A�f�M�ω��ŋC�̂��c��(�f�M�c���ƌ���)���O���ɐ����d��������(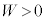 )�ƁA
)�ƁA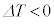 �ƂȂ�A���x��������܂��B�f�M�ω��ŋC�̂����k(�f�M���k�ƌ���)����ĊO�����琳���d������(
�ƂȂ�A���x��������܂��B�f�M�ω��ŋC�̂����k(�f�M���k�ƌ���)����ĊO�����琳���d������(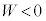 )�ƁA
)�ƁA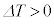 �ƂȂ�A���x���㏸���܂��B
�ƂȂ�A���x���㏸���܂��B
�Ă̏������ɏ㏸�C�����N����Ɛϗ��_����������̂́A�㏸�C���̒f�M�c���̌��ʂɂ�艷�x���������ċ�C���̐����C�����I���邩��ł��B
�܂��A�①�ɂ�G�A�R���̗�p���A��x���k�����C�̂���C�ɖc�������ĉ��x�������邱�Ƃɂ��������Ă��܂��B
�f�M�ω��̉ߒ��̂����Ԃɂ����āA���z�C�̂�������p�C�̐���V�C��������n�C�C�̒萔��R�C��Ή��x��T�Ƃ��āA
��ԕ������F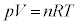 �@����A
�@����A
��������f�M�ω��ŁA�����A�̐��A��Ή��x�������ʕω����A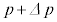 �C
�C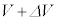 �C
�C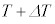 �ɂȂ����Ƃ��āA
�ɂȂ����Ƃ��āA
�ω���̏�ԕ������F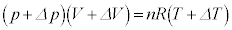
�W�J���āA2���̔�����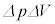 ������ƁA
������ƁA
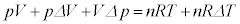 �@����B
�@����B
�B�|�A���A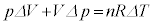 �@����C
�@����C
����A���̔����ȕω��̉ߒ��ŋC�̂̂����d���́A2���̔�����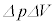 ������ƁA
������ƁA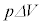 �ƍl�����܂��B�@�ŁA
�ƍl�����܂��B�@�ŁA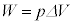 �Ƃ��āA
�Ƃ��āA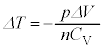
�C�ɑ�����āA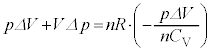
�������āA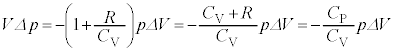 �@(�}�C���[�̊W�����g�p)
�@(�}�C���[�̊W�����g�p)
�����ŁA��M��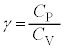 ��p���A����ɗ��ӂ�
��p���A����ɗ��ӂ�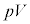 �Ŋ���ƁA
�Ŋ���ƁA
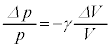
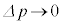 �C
�C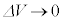 �Ƃ��āA
�Ƃ��āA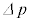 ��
��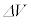 ������L��
������L��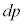 �C
�C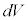 �ɕς��A���ӂ�ϕ�����ƁA
�ɕς��A���ӂ�ϕ�����ƁA
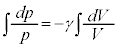
�� 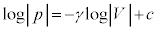 �@(c�͐ϕ��萔)
�@(c�͐ϕ��萔)
�� 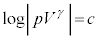
������A�|�A�b�\���̊W��
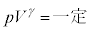
�������܂��B
�|�A�b�\���̊W���Ə�ԕ������́A�Ƃ��ɁA����p�C�̐�V�Ɋւ���W���ł����A�f�M�ω��ɂ����āA�r���I�ɗp����̂ł͂Ȃ��A�A�����ėp���邱���ɒ��ӂ��Ă��������B���҂�g�ݍ��킹�邱�Ƃɂ��A
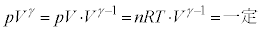
���A�|�A�b�\���̊W���̕ό`
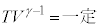
�������܂��B��������L�p�Ȏ��ł��B
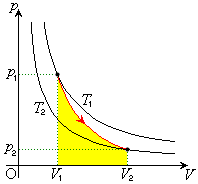 �|�A�b�\���̊W�����A�f�M�ω���p�|V�Ȑ��͉E�}�Ԑ��̂悤�ɂȂ�܂��B
�|�A�b�\���̊W�����A�f�M�ω���p�|V�Ȑ��͉E�}�Ԑ��̂悤�ɂȂ�܂��B
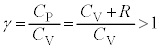
���A�f�M�ω���p�|V�Ȑ��́A�����Ȑ������X�����}�ɂȂ邱�Ƃɒ��ӂ��Ă��������B
�f�M�ω��ŁA�C�̂̑̐ρA���́A��Ή��x���A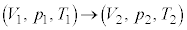 �ƕω�����Ƃ��A
�ƕω�����Ƃ��A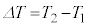 �Ƃ��āA�C�̂̂���d��
�Ƃ��āA�C�̂̂���d��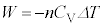 �́A�E�}�̉��F�����̖ʐςɂȂ�܂��B
�́A�E�}�̉��F�����̖ʐςɂȂ�܂��B
(��ԕ��������A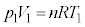 �C
�C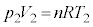 �C�|�A�b�\���̊W�����A
�C�|�A�b�\���̊W�����A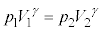 )
)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 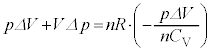
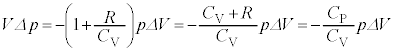 �@(�}�C���[�̊W�����g�p)
�@(�}�C���[�̊W�����g�p)