阪大物理'23年前期[1]
小球の運動や衝突について考える。地点Oにxy平面の原点を、水平方向にx軸を、鉛直上方きにy軸をとり、小球の運動はxy平面に限られるものとする。なお、小球の大きさは無視できるほど小さく、小球の回転は考えないものとし、空気抵抗も無視する。重力加速度の大きさは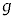 であり、その向きは鉛直下向きである。
であり、その向きは鉛直下向きである。
 I.質量mの小球Aを投げた時の様子を観察する。図1のように、地点Oから仰角θ[rad]の方向に速さ
I.質量mの小球Aを投げた時の様子を観察する。図1のように、地点Oから仰角θ[rad]の方向に速さ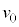 で小球を投げた。ただし、
で小球を投げた。ただし、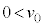 ,
,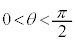 とする。
とする。
問1 小球Aが達する最高点の高さを、m,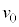 ,θ,
,θ,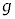 のうち必要なものを用いて表せ。
のうち必要なものを用いて表せ。
問2 小球Aを投げた後、しばらくして小球Aは地面(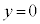 )に落下した。落下地点と地点Oの間の水平距離を、m,
)に落下した。落下地点と地点Oの間の水平距離を、m,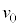 ,θ,
,θ, のうち必要なものを用いて表せ。
のうち必要なものを用いて表せ。
問3 初速度の大きさ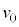 を一定にしたままで、仰角θを変えて小球Aを投げる。地点Oから最も遠くに落下する場合の仰角θ[rad]を求めよ。
を一定にしたままで、仰角θを変えて小球Aを投げる。地点Oから最も遠くに落下する場合の仰角θ[rad]を求めよ。
問4 落下した小球Aは地面に衝突してはね返り、地面との衝突を繰り返した。地面はなめらかな面で、小球Aと地面の衝突は非弾性衝突であり、反発係数をeとする。小球Aが地面にn回目に衝突した地点と地点Oの間の水平距離を、m,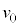 ,θ,
,θ,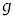 ,e,nのうち必要なものを用いて表せ。
,e,nのうち必要なものを用いて表せ。
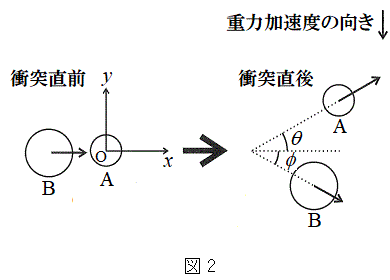 Ⅱ.図2のように、地点Oにxy平面の原点を、水平方向にx軸を、鉛直上向きにy軸をとる。質量Mの小球Bは、地点Oで静止していた質量mの小球Aに衝突する。衝突直前の小球Bの速度は
Ⅱ.図2のように、地点Oにxy平面の原点を、水平方向にx軸を、鉛直上向きにy軸をとる。質量Mの小球Bは、地点Oで静止していた質量mの小球Aに衝突する。衝突直前の小球Bの速度は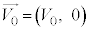 であったが、衝突直後に小球Aの速度は
であったが、衝突直後に小球Aの速度は となり、小球Bの速度は
となり、小球Bの速度は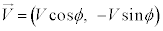 となったとする。ただし、
となったとする。ただし、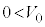 ,
, ,
,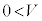 とする。また、図2のように、θ[rad]は
とする。また、図2のように、θ[rad]は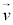 とx軸のなす角度であり、ϕ[rad]は
とx軸のなす角度であり、ϕ[rad]は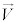 とx軸のなす角度である。
とx軸のなす角度である。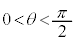 ,
,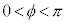 とする。なお、小球Aと小球Bの衝突は弾性衝突である。ただし、小球と地面との衝突は考えないものとする。
とする。なお、小球Aと小球Bの衝突は弾性衝突である。ただし、小球と地面との衝突は考えないものとする。
問5 衝突によってはね上げられた直後の小球Aの速さvをm,M, ,θのうち必要なものを用いて表せ。
,θのうち必要なものを用いて表せ。
問6 小球Aがはね上げられた後、しばらくして小球Aは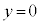 まで落下した。落下地点と地点Oの間の水平距離Lをm,M,
まで落下した。落下地点と地点Oの間の水平距離Lをm,M,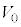 ,θ,
,θ,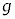 のうち必要なものを用いて表せ。
のうち必要なものを用いて表せ。
問7 距離Lが最も大きくなる場合を考えたい。m,M,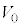 ,
, ,d,
,d,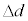 のうち必要なものを用いて、以下の空欄に入るべき数式を解答欄に記せ。
のうち必要なものを用いて、以下の空欄に入るべき数式を解答欄に記せ。  とおくと、Lの値が最大になる時にZの値も最大となる。
とおくと、Lの値が最大になる時にZの値も最大となる。 (
(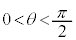 )とおけば、十分に小さいdの変化である
)とおけば、十分に小さいdの変化である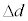 に対して、Zの変化
に対して、Zの変化 は、
は、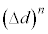 (
(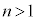 )の項を無視すると、
)の項を無視すると、 と書ける。Zの値が最大となる場合、dの変化
と書ける。Zの値が最大となる場合、dの変化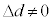 に対して
に対して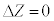 となるので、Lの値が最大になる
となるので、Lの値が最大になる の値は
の値は となる。
となる。
Ⅲ.Ⅱでは、小球Aと小球Bを合わせた2物体の重心Gの位置は、時間とともに移動する。Ⅱの小球Aと小球Bの衝突を、重心Gとともに移動する観測者Pから観察する。なお、小球Aと小球Bの質量はそれぞれmとMである。
問8 観測者Pから見た小球Aと小球Bの運動を求めたい。m,M,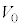 ,
,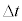 のうち必要なものを用いて、以下の空欄に入るべき数式を解答欄に記せ。
のうち必要なものを用いて、以下の空欄に入るべき数式を解答欄に記せ。 Ⅱの座標系では、小球Aと小球Bの座標をそれぞれ と
と とすれば、2物体の重心Gの座標は
とすれば、2物体の重心Gの座標は と表される。衝突直前に小球Aは地点Oに静止しており、小球Bは水平方向(x軸の正の向き)に速さ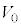 を持っていたので、微小時間
を持っていたので、微小時間 の間における重心Gの座標の変化量は
の間における重心Gの座標の変化量は と表される。ゆえに、重心Gの速度は
と表される。ゆえに、重心Gの速度は となる。よって、衝突直前において、重心Gとともに移動する観測者Pから見た小球Aの速度は
となる。よって、衝突直前において、重心Gとともに移動する観測者Pから見た小球Aの速度は であり、小球Bの速度は
であり、小球Bの速度は となる。
となる。
問9 衝突直後に、観測者Pから見た小球Aの速度は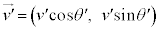 となり、小球Bの速度は
となり、小球Bの速度は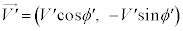 となった。
となった。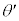 [rad]は
[rad]は とx軸のなす角度であり、
とx軸のなす角度であり、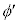 [rad]は
[rad]は とx軸のなす角度である。ただし、
とx軸のなす角度である。ただし、 ,
, とする。衝突直後における小球Aの速さ
とする。衝突直後における小球Aの速さ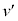 ,小球Bの速さ
,小球Bの速さ ,
,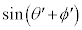 をm,M,
をm,M,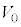 のうち必要なものを用いて表せ。
のうち必要なものを用いて表せ。
問10 小球Bの質量Mが小球Aの質量mより大きい場合、Ⅱの座標系で見た小球Bの角度ϕには上限がある。m,M, のうち必要なものを用いて、
のうち必要なものを用いて、 の上限値を表せ。
の上限値を表せ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 最初の方は教科書の標準問題ですが、Ⅲの相対速度まで行くと、ボリューム満点です。
Ⅰ.問1 小球Aの初速度のy方向成分は ,最高点での速度のy成分は0です。最高点の高さをhとして、y方向について等加速度運動の公式より、
,最高点での速度のy成分は0です。最高点の高さをhとして、y方向について等加速度運動の公式より、 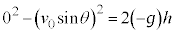 ∴
∴  ......[答]
......[答]
 ∴
∴ 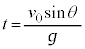
投げてから落下するまでの時間は、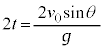 ・・・①
・・・①
この間、小球Aは水平方向に速さ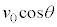 で等速度運動します。落下地点と地点Oの間の水平距離は、①より、
で等速度運動します。落下地点と地点Oの間の水平距離は、①より、 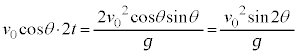 ......[答]
......[答]
問3 問2の結果で、 が最大になるのは、
が最大になるのは、 より、
より、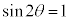 のときで、このとき、
のときで、このとき、 [rad] ......[答]
[rad] ......[答]
問4 n回目の衝突直後の小球Aの速度の鉛直方向成分の大きさを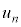 とすると、エネルギー保存より、落下してきたときの速度の鉛直方向成分は
とすると、エネルギー保存より、落下してきたときの速度の鉛直方向成分は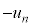 なので、n回目の衝突直前の小球Aの速度の鉛直成分は、
なので、n回目の衝突直前の小球Aの速度の鉛直成分は、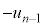 です。ただし、最初に投げたときの初速度の鉛直成分より、
です。ただし、最初に投げたときの初速度の鉛直成分より、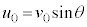 とします。
とします。  ∴
∴ 
よって、数列 は、初項
は、初項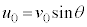 ,公比eの等比数列で、
,公比eの等比数列で、 です。n回目の衝突から
です。n回目の衝突から 回目の衝突までの時間
回目の衝突までの時間 は、①において、
は、①において、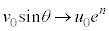 として、
として、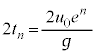
水平方向は速さ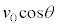 で等速度運動するので、小球Aが地面にn回目に衝突した地点と地点Oの間の水平距離は、
で等速度運動するので、小球Aが地面にn回目に衝突した地点と地点Oの間の水平距離は、 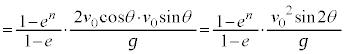 ......[答]
......[答]
Ⅱ.問5 衝突は極めて短時間に起こるので、衝突中に小球に力積を及ぼす外力、また仕事をする外力はなく、衝突前後で運動量、力学的エネルギーは保存されると考えます。
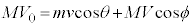 ・・・①
・・・①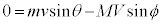 ・・・②
・・・②③× に代入すると、
に代入すると、 mで割り整理すると、
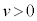 より、衝突直後の小球Aの速さは、
より、衝突直後の小球Aの速さは、 ......[答]
......[答]
問6 問2の結果で、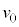 →問5のv,として、落下地点と地点Oの間の水平距離Lは、
→問5のv,として、落下地点と地点Oの間の水平距離Lは、 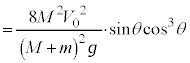 ......[答]
......[答]
問7 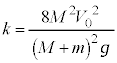 ,
,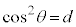 とおくと、
とおくと、 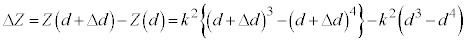 ・・・⑥
・・・⑥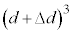 を展開し、
を展開し、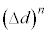 (
(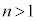 )の項を無視すると、
)の項を無視すると、
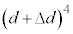 を展開し、
を展開し、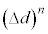 (
(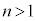 )の項を無視すると、
)の項を無視すると、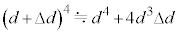
⑥に代入すると、 ......(a)
......(a)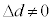 に対して、
に対して、 とすると、
とすると、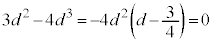
よって、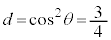 ,
,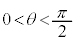 より、
より、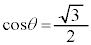
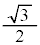 ......(b)
......(b)注.この部分は試験会場では、空所補充問題なので、Zをdで微分して、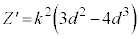 より、
より、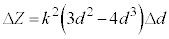 ,Zを最大とするdは、
,Zを最大とするdは、 として
として ,
, において
において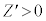 ,
, において
において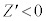 となることから、
となることから、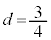 のとき最大(関数の増減を参照)、とするべきです。微積は難しいから近似でやるべきだ、と言う物理の先生がよくいますが、近似の方がよほど難しく計算も大変なことが多いからです。本問がよい例です。
のとき最大(関数の増減を参照)、とするべきです。微積は難しいから近似でやるべきだ、と言う物理の先生がよくいますが、近似の方がよほど難しく計算も大変なことが多いからです。本問がよい例です。
Ⅲ.問8  であり、小球Aは静止していたので
であり、小球Aは静止していたので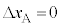 ,小球Bは
,小球Bは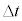 の間に速さ
の間に速さ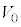 で等速度運動していたので
で等速度運動していたので ,よって、
,よって、  とおくと、重心Gとともに移動する観測者から見た衝突直前の小球Aの速度は、
とおくと、重心Gとともに移動する観測者から見た衝突直前の小球Aの速度は、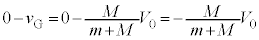
 ......(e)
......(e)小球Bの速度は、
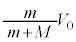 ......(f)
......(f)
問9 小球Aと小球Bを合わせた系には外力は働かず、重心は衝突前も衝突後も等速度運動する(力のつり合いを参照)ので、重心から小球A,Bの運動を見ても運動量は保存します。また、重心から見て重心は静止しています。  ・・・⑦
・・・⑦ ∴
∴  ・・・⑧
・・・⑧⑦に代入すると、
 ∴
∴ 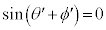 ......[答]
......[答]注.この結果は、重心から見ると、衝突後、小球Aと小球Bは正反対の方向に進む、ということを表しています。
 ,
,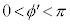 より、
より、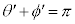 ,これより、
,これより、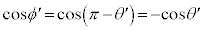 ,
,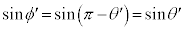 ,⑧より、
,⑧より、 ・・・⑨
・・・⑨
地点Oから見た力学的エネルギー保存の式③を考えます。
重心から見た速度と、地点Oから見た速度について、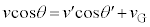 ,
,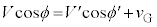 (相対速度を参照)
(相対速度を参照)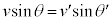 ,
,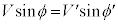 ・・・⑩ (重心は水平方向に動くので、地点Oから見た鉛直成分と重心から見た鉛直成分は一致する)
・・・⑩ (重心は水平方向に動くので、地点Oから見た鉛直成分と重心から見た鉛直成分は一致する)よって、
③に代入すると、
よって、小球Aの速さは、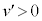 より、
より、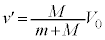 ......[答]⑨より、小球Bの速さは、
......[答]⑨より、小球Bの速さは、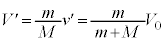 ......[答]
......[答]
問10 ⑩より、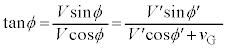 ・・・⑪
・・・⑪  (問9の結果と問8(d)より)
(問9の結果と問8(d)より)
 ここで、
ここで、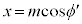 ,
,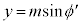 と見ると、
と見ると、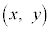 は原点を中心とする半径mの円周上の点で、
は原点を中心とする半径mの円周上の点で、 は、円周上の点と
は、円周上の点と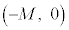 を結ぶ直線の傾きです(円の媒介変数表示を参照)。これが最大になるのは。この直線が円の接線になるときで、このとき、
を結ぶ直線の傾きです(円の媒介変数表示を参照)。これが最大になるのは。この直線が円の接線になるときで、このとき、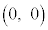 と
と と接点とで直角三角形となり、
と接点とで直角三角形となり、 と接点との距離は
と接点との距離は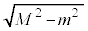 ,このときの直線の傾きは
,このときの直線の傾きは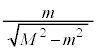 (右図参照),よって、
(右図参照),よって、 の上限値は、
の上限値は、 ......[答]
......[答]
注.受験生には物珍しい本問ですが、ネタになっている問題(以下)があり、この問題を知っていれば、上記のような面倒な計算をせずとも、ベクトル図を描いて解決します。
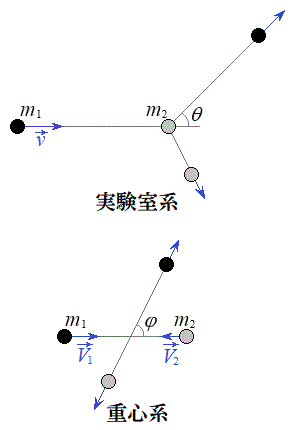 質量
質量 の物体1が、空間に静止している質量
の物体1が、空間に静止している質量 の物体2に、速度
の物体2に、速度 で接近し衝突した。衝突は完全に弾性的であり、全運動エネルギーの変化はなかった。物体1,2の位置を示すベクトルがそれぞれ
で接近し衝突した。衝突は完全に弾性的であり、全運動エネルギーの変化はなかった。物体1,2の位置を示すベクトルがそれぞれ ,
, であるとき、ベクトル
であるとき、ベクトル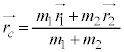 で与えられる点を両物体の重心と呼ぶ。重心は実験室空間を等速直線運動するが、この重心と共に動く座標系を重心系、実験室空間に固定されている座標系を実験室系と呼ぶことにする。
で与えられる点を両物体の重心と呼ぶ。重心は実験室空間を等速直線運動するが、この重心と共に動く座標系を重心系、実験室空間に固定されている座標系を実験室系と呼ぶことにする。
重心系のように実験室系に対して等速直線運動している座標系においても、運動量の保存則・力学的エネルギーの保存則など実験室系で成り立つ力学法則は全く同様に成り立つとしてよい。(1) 実験室系における重心の速度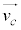 を
を ,
,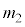 ,
,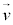 で表し、さらに重心系における衝突前の物体1,2の速度
で表し、さらに重心系における衝突前の物体1,2の速度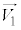 ,
,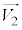 を求めよ。
を求めよ。 (2) 重心系においては衝突の前後で各物体の速度の大きさが変化しないことを示せ。
(3) 衝突前後における物体1の運動方向の変化角度が、実験室系ではθ,重心系ではφであったとする。両者の間には次の関係があることを示せ。ただし、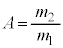 とする。
とする。 以下略 (東大92年後期[1])
阪大23年[1]では、問題文には何も書かれておらず、受験生が自力で、重心系でも運動量保存と、エネルギー保存が成立することを考慮して解くようになっていますが、東大の問題では問題文にヒントとして与えられています。
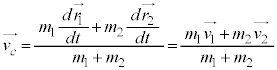 ・・・①
・・・①衝突前においては、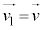 ,
, だったので、①より、
だったので、①より、 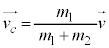 ......[答]
......[答]
 ......[答] (相対速度を参照)
......[答] (相対速度を参照)
 ......[答]
......[答]これより、
 ・・・②
・・・②つまり、重心から見た衝突前の物体1,2の運動量の和は0です(重心から重心を見れば静止しているので当然ですが)。
(2) 重心系における衝突後の物体1,2の速度を ,
, として、②を用いると、運動量保存より、
として、②を用いると、運動量保存より、  ∴
∴ 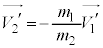
つまり、 と
と は一直線上で正反対の方向を向いています。ベクトルで運動量保存を考えれば、上記阪大の問題の速さについての⑨式は簡単に求められます。
は一直線上で正反対の方向を向いています。ベクトルで運動量保存を考えれば、上記阪大の問題の速さについての⑨式は簡単に求められます。
 重心系において、衝突は完全に弾性的なので、右上図のようなベクトル図が得られます(衝突・合体・分裂の問題を参照)。
重心系において、衝突は完全に弾性的なので、右上図のようなベクトル図が得られます(衝突・合体・分裂の問題を参照)。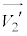 と
と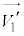 が一直線上なので、両者の速度の衝突面方向成分は衝突前後で変化しません。
が一直線上なので、両者の速度の衝突面方向成分は衝突前後で変化しません。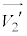 と
と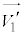 が一直線上なので、衝突面と速度のなす角の大きさ(
が一直線上なので、衝突面と速度のなす角の大きさ(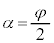 )も変化しません。当然、衝突面と垂直な方向について、反発係数を1とした反発係数の式、
)も変化しません。当然、衝突面と垂直な方向について、反発係数を1とした反発係数の式、 が成立します。この式を解かなくても、右上のベクトル図より、
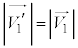 ,
,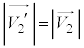
は明らかです。これで、上記阪大の問9も簡単に求められます。
(3) 実験室系の物体1の衝突後の速度を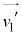 とすると、
とすると、 これより、右下図のようなベクトル図が得られます。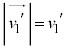 ,
,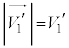 ,
,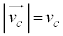 とすると、ベクトル図より、
とすると、ベクトル図より、 となり、上記阪大の問題の⑪式が得られます。 として、
として、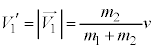 ,
,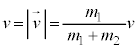 より、
より、 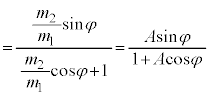 ......[答]
......[答]
実はこの東大の問題にも元ネタがあり、例えば、小出昭一郎さん(悩める受験生だった私を量子力学へと導いてくれた先生です。大学でも物理学を受講しました)の「力学」(岩波書店・物理テキストシリーズ1)の94,95ページに出ています。東大の方の解答は、この本に即したものです。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
 となる。よって、衝突直前において、重心Gとともに移動する観測者Pから見た小球Aの速度は
となる。よって、衝突直前において、重心Gとともに移動する観測者Pから見た小球Aの速度は ......[答]
......[答]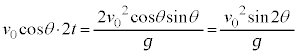 ......[答]
......[答] が最大になるのは、
が最大になるのは、 ∴
∴ 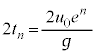
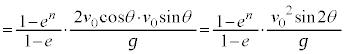 ......[答]
......[答]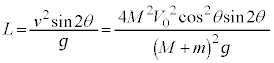
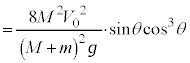 ......[答]
......[答]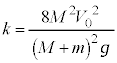 ,
,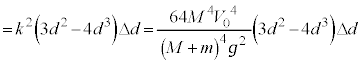
 ......(a)
......(a)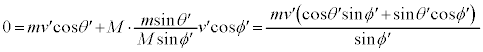
 ∴
∴  (問9の結果と問8(d)より)
(問9の結果と問8(d)より)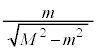 (右図参照),よって、
(右図参照),よって、 ......[答]
......[答]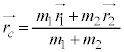 で与えられる点を両物体の重心と呼ぶ。重心は実験室空間を等速直線運動するが、この重心と共に動く座標系を重心系、実験室空間に固定されている座標系を実験室系と呼ぶことにする。
で与えられる点を両物体の重心と呼ぶ。重心は実験室空間を等速直線運動するが、この重心と共に動く座標系を重心系、実験室空間に固定されている座標系を実験室系と呼ぶことにする。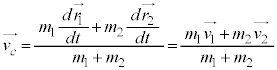 ・・・①
・・・①

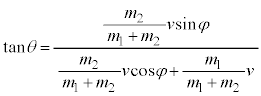
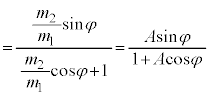 ......[答]
......[答]