��啨��'23�N�O��[2]
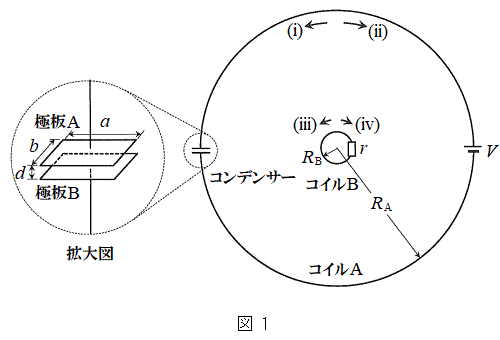 �}1�̂悤�ɁA�^�ɔ��a�����ꂼ��
�}1�̂悤�ɁA�^�ɔ��a�����ꂼ��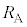 �����
�����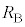 �̈ꊪ���̉~�`�R�C��A�����B������ʓ��ɒ��S�����낦�Ēu����Ă���A�R�C��A�ɂ͕��s�R���f���T�[�ƋN�d��V�̒����d�����A�R�C��B�ɂ͒�R�lr�̒�R���A���ꂼ��ڑ�����Ă���B�R���f���T�[�́A�ӂ̒�����a�Cb�̒����`�̋ɔ�A����ыɔ�B�ō\������A�ɔԂ̋�����d�ł���A�ɔԂ͐^��ł���B�����ŁAd��a�Cb�ɔ�ׂď\���������A�ɔ[���̓d�E�̌��ʂ͖����ł���Ƃ���B�܂��A�R�C��A�����B�̓d�C��R�������ł���Ƃ���B�����ł́A�R���f���T�[�A�����d���A��R�̃T�C�Y�̓R�C���̔��a�ɔ�ׂď\���������A�R�C���͉~�`�R�C���Ƃ݂Ȃ��Ď��E���v�Z���Ă悢�B�ȉ��ł́A�^��̗U�d������ѓ����������ꂼ��
�̈ꊪ���̉~�`�R�C��A�����B������ʓ��ɒ��S�����낦�Ēu����Ă���A�R�C��A�ɂ͕��s�R���f���T�[�ƋN�d��V�̒����d�����A�R�C��B�ɂ͒�R�lr�̒�R���A���ꂼ��ڑ�����Ă���B�R���f���T�[�́A�ӂ̒�����a�Cb�̒����`�̋ɔ�A����ыɔ�B�ō\������A�ɔԂ̋�����d�ł���A�ɔԂ͐^��ł���B�����ŁAd��a�Cb�ɔ�ׂď\���������A�ɔ[���̓d�E�̌��ʂ͖����ł���Ƃ���B�܂��A�R�C��A�����B�̓d�C��R�������ł���Ƃ���B�����ł́A�R���f���T�[�A�����d���A��R�̃T�C�Y�̓R�C���̔��a�ɔ�ׂď\���������A�R�C���͉~�`�R�C���Ƃ݂Ȃ��Ď��E���v�Z���Ă悢�B�ȉ��ł́A�^��̗U�d������ѓ����������ꂼ��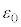 �����
�����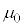 �Ƃ���B
�Ƃ���B
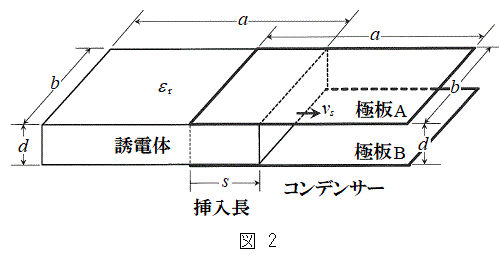 �T�D���܁A�}1���̃R���f���T�[�̋ɔ��ɁA�}2�̂悤�ɁA�ӂ̒�����a�Cb�Cd�̒����̗̂U�d�̂�}������B�U�d�̂̑}������}2�Ɏ����悤��s�Ƃ���B�U�d�̂�
�T�D���܁A�}1���̃R���f���T�[�̋ɔ��ɁA�}2�̂悤�ɁA�ӂ̒�����a�Cb�Cd�̒����̗̂U�d�̂�}������B�U�d�̂̑}������}2�Ɏ����悤��s�Ƃ���B�U�d�̂�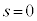 �̒n�_����A�����x��0�C�����x�̑傫����p (
�̒n�_����A�����x��0�C�����x�̑傫����p (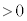 )�œ������x�^��������ƃR�C��B�ɓd�������ꂽ�B�U�d�̂̑}������
)�œ������x�^��������ƃR�C��B�ɓd�������ꂽ�B�U�d�̂̑}������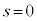 �̂Ƃ��̎�����
�̂Ƃ��̎�����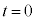 �Ƃ���B�ȉ��̖�ɓ�����B�����ŁA�R�C��A�̎��ȗU���ɂ��t�N�d�͂͏����������ł���Ƃ��A�܂��A�R�C��B�ɗ����d������鎥�E���キ�����ł���Ƃ���B�Ȃ��A�U�d�̂̔�U�d����
�Ƃ���B�ȉ��̖�ɓ�����B�����ŁA�R�C��A�̎��ȗU���ɂ��t�N�d�͂͏����������ł���Ƃ��A�܂��A�R�C��B�ɗ����d������鎥�E���キ�����ł���Ƃ���B�Ȃ��A�U�d�̂̔�U�d����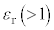 �ł���A�U�d�̒[���̓d�E�̌��ʂ͖����ł���Ƃ���B
�ł���A�U�d�̒[���̓d�E�̌��ʂ͖����ł���Ƃ���B
��1�@�U�d�̂̑}������s (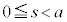 )�̂Ƃ��ɃR���f���T�[�ɒ~�����Ă���d�C�ʂ�a�Cb�Cd�Cs�C
)�̂Ƃ��ɃR���f���T�[�ɒ~�����Ă���d�C�ʂ�a�Cb�Cd�Cs�C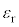 �C
�C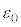 �CV�̂����K�v�Ȃ��̂�p���ĕ\���B
�CV�̂����K�v�Ȃ��̂�p���ĕ\���B
��2�@���܁A����t �����������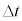 �̊ԂɁA�U�d�̂̑}������s����
�̊ԂɁA�U�d�̂̑}������s����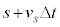 �ɕω������Ƌߎ����āA���̊ԂɃR�C��A�ɗ����d���̑傫��
�ɕω������Ƌߎ����āA���̊ԂɃR�C��A�ɗ����d���̑傫��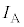 ��
��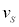 �Ca�Cb�Cd�C
�Ca�Cb�Cd�C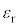 �C
�C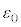 �CV�̂����K�v�Ȃ��̂�p���ĕ\���B�����ŁA
�CV�̂����K�v�Ȃ��̂�p���ĕ\���B�����ŁA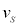 (
(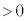 )�͑}������s�̂Ƃ��̗U�d�̂̑��x�ł���B�܂��A���̓d���̌�����}1���̋L��(i)�܂���(ii)�ɂ�莦���B
)�͑}������s�̂Ƃ��̗U�d�̂̑��x�ł���B�܂��A���̓d���̌�����}1���̋L��(i)�܂���(ii)�ɂ�莦���B
��3�@����t �ɂ����ēd��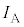 ���R�C���̒��S�ɂ��鎥�E�̋�����
���R�C���̒��S�ɂ��鎥�E�̋�����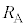 �C
�C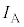 �C
�C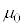 �̂����K�v�Ȃ��̂�p���ĕ\���B�܂����̌����́A�}1�ɂ�����(�A)���ʕ\���痠�̌����A���邢��(�C)���ʗ�����\�̌����A�̂����ǂ���ł��邩�B(�A)�܂���(�C)�̋L���Ŏ����B
�̂����K�v�Ȃ��̂�p���ĕ\���B�܂����̌����́A�}1�ɂ�����(�A)���ʕ\���痠�̌����A���邢��(�C)���ʗ�����\�̌����A�̂����ǂ���ł��邩�B(�A)�܂���(�C)�̋L���Ŏ����B
��4�@����t �����������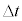 �̊ԂɗU�d�̂̑��x��
�̊ԂɗU�d�̂̑��x��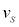 ����
����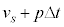 �ɂȂ����Ƃ��āA���̊ԂɃR�C��B�ɗ����d��
�ɂȂ����Ƃ��āA���̊ԂɃR�C��B�ɗ����d��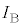 �̑傫����r�C
�̑傫����r�C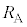 �C
�C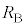 �Ca�Cb�Cd�Cp�C
�Ca�Cb�Cd�Cp�C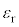 �C
�C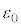 �C
�C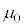 �CV�̂����K�v�Ȃ��̂�p���ĕ\���B�܂��A���̓d���̌�����}1���̋L��(iii)�܂���(iv)�ɂ�莦���B�������A�R�C��B�̔��a
�CV�̂����K�v�Ȃ��̂�p���ĕ\���B�܂��A���̓d���̌�����}1���̋L��(iii)�܂���(iv)�ɂ�莦���B�������A�R�C��B�̔��a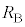 �̓R�C��A�̔��a
�̓R�C��A�̔��a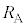 �ɔ�ׂď\���������A�R�C��B�̓����̎��E�͈�l�Œ��S�̒l�ɓ������Ƃ���B
�ɔ�ׂď\���������A�R�C��B�̓����̎��E�͈�l�Œ��S�̒l�ɓ������Ƃ���B ��5�@�U�d�̂�}�����n�߂�����ɃR�C��B�ɗ����d���̑傫����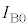 �Ƃ��āA�U�d�̂̑}������0����a�܂ŕω�����Ԃɒ�Rr�ŏ�����G�l���M�[��r�C
�Ƃ��āA�U�d�̂̑}������0����a�܂ŕω�����Ԃɒ�Rr�ŏ�����G�l���M�[��r�C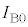 �Ca�Cp�̂����K�v�Ȃ��̂�p���ĕ\���B
�Ca�Cp�̂����K�v�Ȃ��̂�p���ĕ\���B
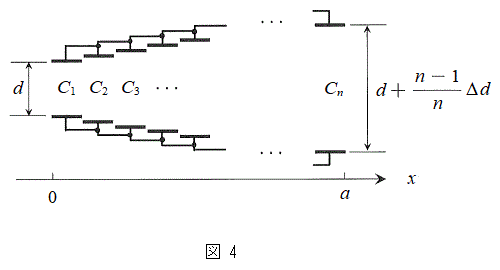 ��6�@���̂Ƃ��́A���̃R���f���T�[�̓d�C�e�ʂ��A�}4�̂悤�ɋɔ�n�̔�����Ԃɓ��������Ăł����A�d�C�e�ʂ�
��6�@���̂Ƃ��́A���̃R���f���T�[�̓d�C�e�ʂ��A�}4�̂悤�ɋɔ�n�̔�����Ԃɓ��������Ăł����A�d�C�e�ʂ�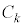 �̔������s�R���f���T�[�����������d�C�e�ʂł���ƍl���悤�B������k��1����n�܂ł̐����ł���B���̕��͂̋ɓ����ׂ����������ɋL���B
�̔������s�R���f���T�[�����������d�C�e�ʂł���ƍl���悤�B������k��1����n�܂ł̐����ł���B���̕��͂̋ɓ����ׂ����������ɋL���B
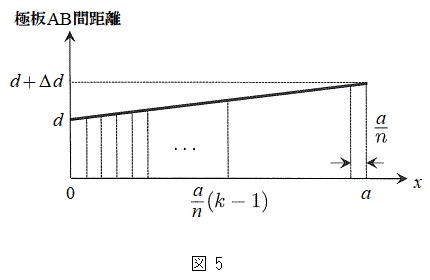 �ɔ�AB�Ԃ̋����͐}5�Ɏ���x��1�����ŕ\�����B���_�����琔����k�Ԗڂ̔������s�R���f���T�[�̋ɔԂ̋�����
�ɔ�AB�Ԃ̋����͐}5�Ɏ���x��1�����ŕ\�����B���_�����琔����k�Ԗڂ̔������s�R���f���T�[�̋ɔԂ̋�����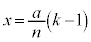 �ɂ�����ɔ�AB�Ԃ̋����ł���Ƃ���A���̋ɔԂ̋�����d�C
�ɂ�����ɔ�AB�Ԃ̋����ł���Ƃ���A���̋ɔԂ̋�����d�C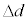 �Cn�Ck��p����
�Cn�Ck��p���� �ƕ\�����B���������āA�������s�R���f���T�[�̍����e�ʂ�a�Cb�Cd�C
�ƕ\�����B���������āA�������s�R���f���T�[�̍����e�ʂ�a�Cb�Cd�C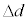 �Cn�Ck�C
�Cn�Ck�C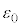 ��p����
��p����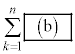 �ƕ\�����B���܁A������n���\���傫���Ƃ��̔������s�R���f���T�[�̍����e�ʂ́A���̋ߎ���K�p�����a�Cb�Cd�C
�ƕ\�����B���܁A������n���\���傫���Ƃ��̔������s�R���f���T�[�̍����e�ʂ́A���̋ߎ���K�p�����a�Cb�Cd�C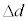 �C
�C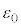 ��p����
��p���� �ƕ\�����Bn���\���傫���A����δ��1�ɔ�ׂď\���������ꍇ�F
�ƕ\�����Bn���\���傫���A����δ��1�ɔ�ׂď\���������ꍇ�F
��7�@�}1�̂悤�ɒ����d���ƃR���f���T�[�͂Ȃ����Ă���B�ʒux�ɂ�����ɔ�A��̒P�ʖʐς�����̓d�C�ʂ�x�Ca�Cd�C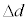 �C
�C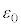 �CV�̂����K�v�Ȃ��̂�p���ĕ\���B
�CV�̂����K�v�Ȃ��̂�p���ĕ\���B
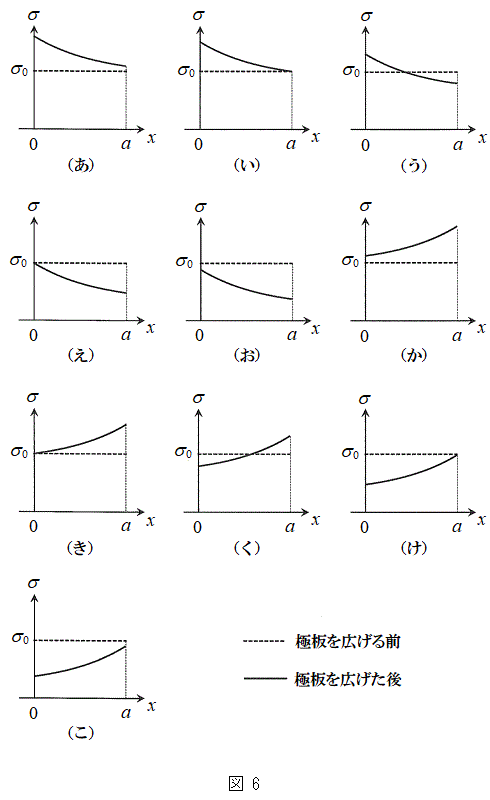 ��8�@������x�C�c�����ɔ�A��̒P�ʖʐς�����̓d�C��σ�Ƃ��āA�ό`�O�ƕό`���σ�̕��z���O���t�ɕ`���Ƃǂ̂悤�ɂȂ邩�B�}6����(��)����(��)�̒�����ł��K�Ȃ��̂�I�ׁB�������A�}����
��8�@������x�C�c�����ɔ�A��̒P�ʖʐς�����̓d�C��σ�Ƃ��āA�ό`�O�ƕό`���σ�̕��z���O���t�ɕ`���Ƃǂ̂悤�ɂȂ邩�B�}6����(��)����(��)�̒�����ł��K�Ȃ��̂�I�ׁB�������A�}����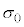 �͋ɔ��L����O�̋ɔ�A��̒P�ʖʐς�����̓d�C�ʂł���B
�͋ɔ��L����O�̋ɔ�A��̒P�ʖʐς�����̓d�C�ʂł���B
��9�@��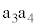 �ƕ�
�ƕ�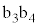 ���㉺�ɓ������L����ہA���ꂼ��̕ӂ̏����x��0�C�����x�̑傫����
���㉺�ɓ������L����ہA���ꂼ��̕ӂ̏����x��0�C�����x�̑傫����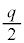 �ň��Ƃ���B�ɔ��L���n�߂�����ɃR�C��B�ɗ����d���̑傫����r�C
�ň��Ƃ���B�ɔ��L���n�߂�����ɃR�C��B�ɗ����d���̑傫����r�C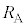 �C
�C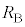 �Ca�Cb�Cd�Cq�C
�Ca�Cb�Cd�Cq�C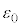 �C
�C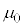 �CV�̂����K�v�Ȃ��̂�p���ĕ\���B
�CV�̂����K�v�Ȃ��̂�p���ĕ\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�~�`�R�C���ɐڑ�����Ă���R���f���T�[�̋ɔԂ��L����Ƃ��A��[���Œ肵�đ��[�����������x�^��������悤�ɍL����ƁA������̉~�`�R�C���ɗ����d���͂ǂ��Ȃ邩�A�Ƃ������ł����A�{�����[�����_�ł��B�o��҂͐e�ł����ď����Ă���̂��Ǝv���܂����A��蕶���́u�d���̑傫��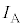 �v�A�u�d��
�v�A�u�d��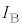 �̑傫���v�ɂ����ӂ��Ă��������B
�̑傫���v�ɂ����ӂ��Ă��������B
�T�D�U�d���̑}�����́A�����xp�C�����x0�C����t ��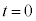 �̂Ƃ�
�̂Ƃ�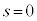 �Ȃ̂ŁA
�Ȃ̂ŁA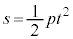 �@����@�@�ŗ^�����܂��B
�@����@�@�ŗ^�����܂��B ��1�@�}������s�̂Ƃ��A�U�d�̂��}������Ă��镔���ɂł��Ă����R���f���T�[�̐Ód�e�ʂ�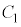 �C�U�d�̂��}������Ă��Ȃ������ɂł��Ă���R���f���T�[�̐Ód�e�ʂ�
�C�U�d�̂��}������Ă��Ȃ������ɂł��Ă���R���f���T�[�̐Ód�e�ʂ�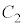 �Ƃ���ƁA
�Ƃ���ƁA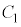 �̋ɔʐς�
�̋ɔʐς�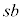 �C
�C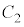 �̋ɔʐς�
�̋ɔʐς�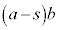 �ŁA���ꂼ��̐Ód�e�ʂ́A
�ŁA���ꂼ��̐Ód�e�ʂ́A 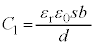 �C
�C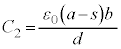
�R���f���T�[���[�̓d����V�ŁA�R���f���T�[�ɒ~�����Ă���d�C��Q�́A
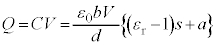 ......[��]
......[��]
��2�@�}������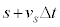 �̂Ƃ��̃R���f���T�[�̓d�C��
�̂Ƃ��̃R���f���T�[�̓d�C��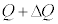 �́A��1�̌��ʂŁA
�́A��1�̌��ʂŁA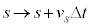 �Ƃ��āA
�Ƃ��āA 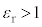 �C
�C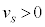 �Ȃ̂�
�Ȃ̂�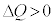 �ł��B����āA�R�C��A�ɗ�����d���̑傫��
�ł��B����āA�R�C��A�ɗ�����d���̑傫��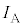 �́A
�́A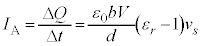 ......[��]
......[��]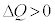 �Ȃ̂ŁA�R���f���T�[�̓d�C�ʂ�����������ɓd��������܂��B�d���̌�����(i) ......[��]
�Ȃ̂ŁA�R���f���T�[�̓d�C�ʂ�����������ɓd��������܂��B�d���̌�����(i) ......[��]
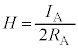 ......[��]�@(
......[��]�@(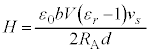 )
)���E�̌����́A�E�˂��̖@�����A���ʗ�����\�̌�����(�C) ......[��]
��4�@�R�C���̒��S��ʉ߂����������x�̑傫��B��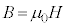 �C�R�C��B���͂ޖʐς�
�C�R�C��B���͂ޖʐς�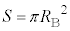 (�����)�Ƃ��āA�R�C��B�����̎��E�͈�l�ƍl����̂ŁA�R�C����ʉ߂��鎥����
(�����)�Ƃ��āA�R�C��B�����̎��E�͈�l�ƍl����̂ŁA�R�C����ʉ߂��鎥����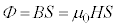 �C��������
�C��������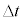 �̊ԂɃR�C��B�ɐ������N�d���̑傫��
�̊ԂɃR�C��B�ɐ������N�d���̑傫��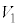 �́A��3�̌��ʂ�p���āA
�́A��3�̌��ʂ�p���āA ��������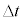 �̊ԂɁA�U�d�̂����x��
�̊ԂɁA�U�d�̂����x��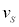 ����
����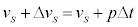 �܂ŕς��Ƃ���
�܂ŕς��Ƃ���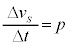 ���A�N�d��
���A�N�d��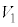 �́A
�́A �R�C��B�ɗ�����d��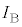 �̑傫���́A
�̑傫���́A 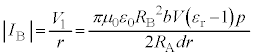 ......[��]
......[��]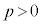 ���
���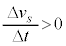 �C��3�̌��ʂ��l������ƁA�R�C��B���т����ʗ�����\�Ɍ����������̎��E�������Ȃ�̂ŁA�N�d�͎͂��E����߂����(�����c�̖@�����Q��)�A�܂�A���ʕ\���痠�Ɍ��������E���������ŁA�E�˂��̖@�����d���̌�����(iv) ......[��]
�C��3�̌��ʂ��l������ƁA�R�C��B���т����ʗ�����\�Ɍ����������̎��E�������Ȃ�̂ŁA�N�d�͎͂��E����߂����(�����c�̖@�����Q��)�A�܂�A���ʕ\���痠�Ɍ��������E���������ŁA�E�˂��̖@�����d���̌�����(iv) ......[��]
��5�@����t �̊Ԃɑ}������0����a�܂ŕω�����Ƃ��ć@���A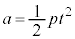
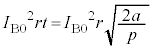 ......[��]
......[��]
�U�D��6�@�������s�R���f���T�[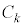 �̋ɔԋ�����
�̋ɔԋ�����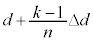 ......(a)
......(a) �������s�R���f���T�[�̍����e��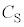 ��
��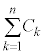 �ł����A
�ł����A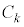 �̋ɔʐς�
�̋ɔʐς�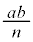 �ŁA
�ŁA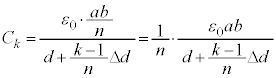 ......(b)
......(b) 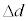 ��d�ɔ�ׂď[���ɏ������̂ŁA
��d�ɔ�ׂď[���ɏ������̂ŁA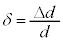 �ƌ��āA��蕶�̋ߎ�����p����ƁA
�ƌ��āA��蕶�̋ߎ�����p����ƁA����āA
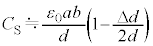 ......(c)
......(c)
��7�@�������s�R���f���T�[�ɒ~������d�C��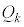 �́A(b)���A
�́A(b)���A �P�ʖʐϓ�����̓d�C�ʂ́A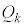 ��
��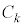 �̖ʐ�
�̖ʐ�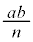 �Ŋ���A��蕶�̐}5��
�Ŋ���A��蕶�̐}5��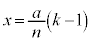 �C�܂�A
�C�܂�A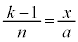 ��p����
��p���� 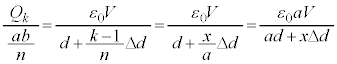 ......[��]
......[��]
��8�@��7�̌��ʂ��A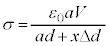 �@����A�@�ƂȂ�܂��B
�@����A�@�ƂȂ�܂��B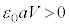 �C
�C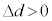 ���A
���A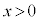 �͈̔͂�
�͈̔͂�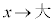 �̂Ƃ�
�̂Ƃ�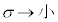 �ł��B�����Ȃ��Ă���O���t��(��)�`(��)�ł��B
�ł��B�����Ȃ��Ă���O���t��(��)�`(��)�ł��B ��1�̌��ʂ�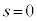 �Ƃ����
�Ƃ����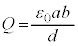 �ƂȂ�A�ɔʐ�
�ƂȂ�A�ɔʐ�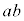 �Ŋ���ƁA�ɔ��L����O�̋ɔ�A��̒P�ʖʐς�����̓d�C�ʂ�
�Ŋ���ƁA�ɔ��L����O�̋ɔ�A��̒P�ʖʐς�����̓d�C�ʂ�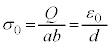 �C�A��
�C�A��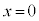 �Ƃ����
�Ƃ����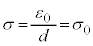 �ƂȂ�܂��B�����Ȃ��Ă���O���t��(��) ......[��]
�ƂȂ�܂��B�����Ȃ��Ă���O���t��(��) ......[��]
��9�@��6(c)���A�R���f���T�[�̐Ód�e�ʂ�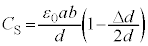 �@����B�@�ł��B��
�@����B�@�ł��B��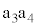 �ƕ�
�ƕ�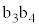 ���㉺�ɓ������L����ہA���ꂼ��̕ӂ̏����x��0�C�����x�̑傫����
���㉺�ɓ������L����ہA���ꂼ��̕ӂ̏����x��0�C�����x�̑傫����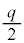 �ň��Ƃ���ƁA��
�ň��Ƃ���ƁA��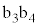 ���猩����
���猩����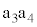 �̉����x��q�ƂȂ�A
�̉����x��q�ƂȂ�A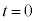 �ɂ�����
�ɂ�����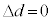 �ł��邱�Ƃ���A����t �ɂ�����
�ł��邱�Ƃ���A����t �ɂ�����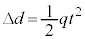 �ł��B����ćB���A
�ł��B����ćB���A �R���f���T�[�ɒ~������d�C��Q�́A
�R���f���T�[�ɗ��ꍞ�ޓd��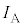 �́A
�́A 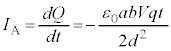 �@(�d���̌����͐}1��(ii)�ł�)
�@(�d���̌����͐}1��(ii)�ł�)�R�C��A�̒��S�ɔ������鎥�E�́A
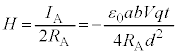 �@(���E�̌����͎��ʕ\���痠�ł�)
�@(���E�̌����͎��ʕ\���痠�ł�)�R�C��B���т�����Φ�́A�R�C��B���͂ޖʐ�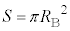 �C�������x�̑傫����
�C�������x�̑傫����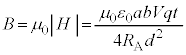 �ł��邱�Ƃ���A
�ł��邱�Ƃ���A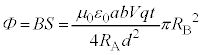
�R�C��B�ɔ�������N�d�͂̑傫��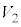 �́A
�́A �R�C��B�ɗ����d���̑傫��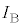 �́A
�́A 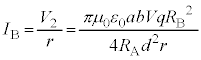 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 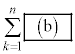 �ƕ\�����B���܁A������n���\���傫���Ƃ��̔������s�R���f���T�[�̍����e�ʂ́A���̋ߎ���K�p�����a�Cb�Cd�C
�ƕ\�����B���܁A������n���\���傫���Ƃ��̔������s�R���f���T�[�̍����e�ʂ́A���̋ߎ���K�p�����a�Cb�Cd�C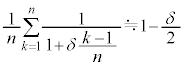
 )
)
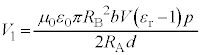
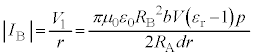 ......[��]
......[��]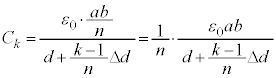 ......(b)
......(b)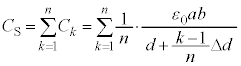
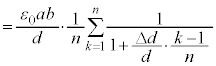
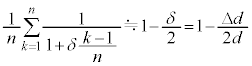
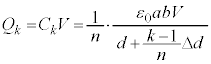
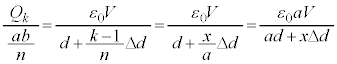 ......[��]
......[��]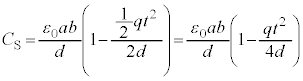
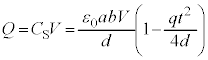
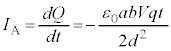 �@(�d���̌����͐}1��(ii)�ł�)
�@(�d���̌����͐}1��(ii)�ł�)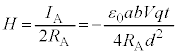 �@(���E�̌����͎��ʕ\���痠�ł�)
�@(���E�̌����͎��ʕ\���痠�ł�)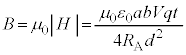 �ł��邱�Ƃ���A
�ł��邱�Ƃ���A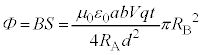
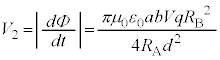
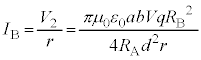 ......[��]
......[��]