���k�啨��'96�N[2]
�d�C�e��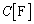 �̃R���f���T�[�Ɍ𗬓d��
�̃R���f���T�[�Ɍ𗬓d��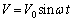 (
(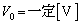 �C
�C �C
�C )��������ƁA�R���f���T�[�ɗ����d��
)��������ƁA�R���f���T�[�ɗ����d��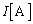 �́A
�́A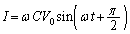 �ŕ\�����B�R���f���T�[�̃��A�N�^���X��
�ŕ\�����B�R���f���T�[�̃��A�N�^���X��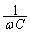 �ł���B�܂��A���ȃC���_�N�^���X
�ł���B�܂��A���ȃC���_�N�^���X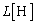 �̃R�C���Ɍ𗬓d��
�̃R�C���Ɍ𗬓d��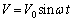 ��������ƁA�R�C���ɗ����d��I��
��������ƁA�R�C���ɗ����d��I��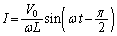 �ŕ\�����B�R�C���̃��A�N�^���X��
�ŕ\�����B�R�C���̃��A�N�^���X��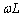 �ł���B�𗬉�H�ɂ��ĉ��L�̖₢�ɓ�����B�@�A�@�C�@�I�@�C�@�J�@�C�@�N�@�`�@�R�@�ɂ͎����A�@�C�@�`�@�G�@�ɂ͐��l(�L������2���܂�)���A�@�T�@�C�@�V�@�ɂ͓K���Ȍ��t���L������B�Ȃ��A�@�L�@�C�@�X�@�͐}�Ŏ����B
�ł���B�𗬉�H�ɂ��ĉ��L�̖₢�ɓ�����B�@�A�@�C�@�I�@�C�@�J�@�C�@�N�@�`�@�R�@�ɂ͎����A�@�C�@�`�@�G�@�ɂ͐��l(�L������2���܂�)���A�@�T�@�C�@�V�@�ɂ͓K���Ȍ��t���L������B�Ȃ��A�@�L�@�C�@�X�@�͐}�Ŏ����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�𗬉�H�Ɋւ����{���ł����A���������̓_�ł�����Ɠ���J��������܂��B
�𗬂ł́A��RR�C�R�C��L�C�R���f���T�[C��ڑ������Ƃ��������C���s�[�_���X�́A���ꂼ����C���s�[�_���X(��RR�C�U�����A�N�^���X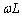 �C�e�ʃ��A�N�^���X
�C�e�ʃ��A�N�^���X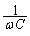 )�̘a
)�̘a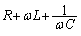 �ł͂Ȃ��A������R�C�c���������
�ł͂Ȃ��A������R�C�c���������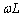 �C�c����������
�C�c����������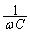 ���Ƃ����Ƃ��̃x�N�g���a�̑傫���Ƃ��āA
���Ƃ����Ƃ��̃x�N�g���a�̑傫���Ƃ��āA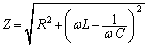 �ƂȂ邱�Ƃɒ��ӂ��Ă��������B
�ƂȂ邱�Ƃɒ��ӂ��Ă��������B
�܂��A�U�����A�N�^���X�A�e�ʃ��A�N�^���X���l����Ƃ��A�d���A�d���̏u���l�ɂ��ẮA�I�[���̖@����K�p�ł��Ȃ�(�ʑ��������)���Ƃɒ��ӂ��Ă��������B�������A�d���A�d���̐U��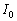 �C
�C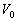 (�]���āA�����l
(�]���āA�����l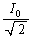 �C
�C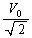 )�ɂ��ẮA�I�[���̖@���Ɨގ��̊W���F
)�ɂ��ẮA�I�[���̖@���Ɨގ��̊W���F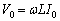 �C
�C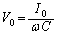 �����藧���܂��B
�����藧���܂��B
(�A) ���ȃC���_�N�^���X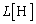 �̃R�C���A�Ód�e��
�̃R�C���A�Ód�e��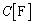 �̃R���f���T�[�A��R
�̃R���f���T�[�A��R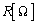 ��ڑ������Ƃ��́A�p���g��
��ڑ������Ƃ��́A�p���g��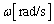 �ɂ������C���s�[�_���X�́A
�ɂ������C���s�[�_���X�́A 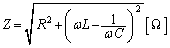 �@����@
�@����@�ŗ^�����܂��B
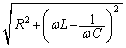 ......[��]
......[��](�C) 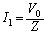 �́AZ�ŏ��̂Ƃ��ɍő�ɂȂ�܂��Bω ���ω�����Ƃ��A�@�ŗ^������Z���ŏ��ɂȂ�̂́A
�́AZ�ŏ��̂Ƃ��ɍő�ɂȂ�܂��Bω ���ω�����Ƃ��A�@�ŗ^������Z���ŏ��ɂȂ�̂́A 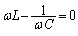 �@����A
�@����A�̂Ƃ��ł��B����āA
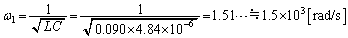
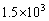 ......[��]
......[��](�E) �A����������Ƃ��@�́A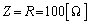 �ƂȂ�܂��B����āA
�ƂȂ�܂��B����āA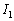 �̍ő�l�́A
�̍ő�l�́A 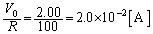
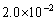 ......[��]
......[��](�G) ���̂Ƃ��AAB�Ԃ��C���s�[�_���X�́A�A���[���ł��B�]���āAAB�Ԃ��d�ʍ����[���ł��B
0 ......[��]
(�I) 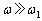 �����
�����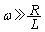 �̂Ƃ��A
�̂Ƃ��A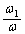 (
(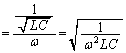 )�C
)�C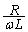 ���o�Ă���悤�ɇ@��ό`���āA
���o�Ă���悤�ɇ@��ό`���āA 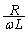 ��
��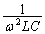 ������ƁA
������ƁA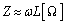
���̂Ƃ���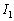 �̑Q�ߌ`�́A
�̑Q�ߌ`�́A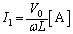
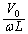 ......[��]
......[��](�J) 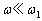 �y��
�y��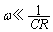 �̂Ƃ��A
�̂Ƃ��A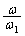 (
(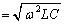 )�C
)�C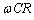 ���o�Ă���悤�ɇ@��ό`���āA
���o�Ă���悤�ɇ@��ό`���āA 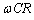 ��
��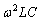 ������ƁA
������ƁA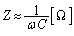
���̂Ƃ���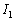 �̑Q�ߌ`�́A
�̑Q�ߌ`�́A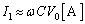
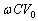 ......[��]
......[��]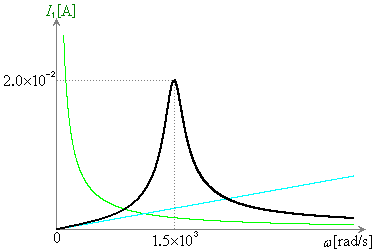 (�L) �����̌��ʂ��ω �̊�
(�L) �����̌��ʂ��ω �̊�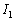 �̊T���͉E�}���F����(���ΐF�̋Ȑ���
�̊T���͉E�}���F����(���ΐF�̋Ȑ���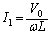 �C���F�̋Ȑ���
�C���F�̋Ȑ���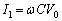 )�B
)�B(�N) ��R���[���d����0�Ȃ̂ŁA�R�C���ƃR���f���T�[�̗��[���𗬓d��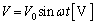 ��������܂��B
��������܂��B ��蕶���A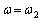 �̂Ƃ��A�R���f���T�[�ɗ�����d���́A
�̂Ƃ��A�R���f���T�[�ɗ�����d���́A 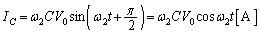 �@����B
�@����B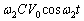 ......[��]
......[��](�P) �R�C���ɗ�����d���́A
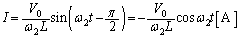 �@����C
�@����C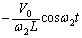 ......[��]
......[��](�R) ��R�𗬂���d����0�Ȃ̂ŁA
�B�C�C���A
�� 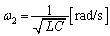
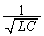 ......[��]
......[��]�R���f���T�[ ......[��]
(�V) 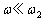 �̂Ƃ��A�R�C�������A�N�^���X
�̂Ƃ��A�R�C�������A�N�^���X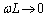 �C�R���f���T�[�����A�N�^���X
�C�R���f���T�[�����A�N�^���X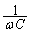 ����C����āA�d���͂قƂ�ǃR�C���𗬂�܂��B
����C����āA�d���͂قƂ�ǃR�C���𗬂�܂��B 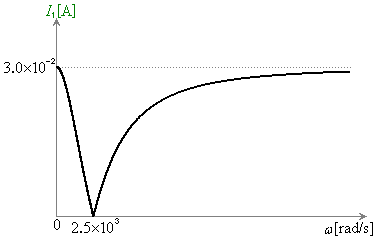 (�X)
(�X) 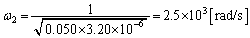
(�T)�̂Ƃ��A�����C���s�[�_���X�́A
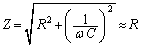 (�R�C���ƃR���f���T�[������ł��邱�Ƃɒ���)
(�R�C���ƃR���f���T�[������ł��邱�Ƃɒ���)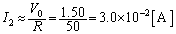
(�V)�̂Ƃ��A�����C���s�[�_���X�́A
�����̌��ʂ��ω �̊�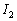 �̊T���͉E�}���F�����B
�̊T���͉E�}���F�����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 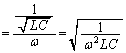 )�C
)�C