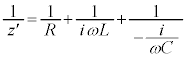インピーダンス 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
抵抗Rと、自己インダクタンスLのコイルと、静電容量Cのコンデンサーが直列に接続された回路に、角周波数ωの交流を流すときのインピーダンスZは、
このときの、電流と電圧の位相のずれδは、電圧の方がδだけ進んでいるとして、
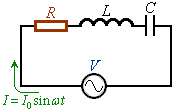 右図のように、交流電源に、抵抗R,自己インダクタンスLのコイル、静電容量Cのコンデンサーを直列に接続した回路を考えます。この回路をRLC直列回路と言います。
右図のように、交流電源に、抵抗R,自己インダクタンスLのコイル、静電容量Cのコンデンサーを直列に接続した回路を考えます。この回路をRLC直列回路と言います。
直列接続なので回路を流れる電流Iは共通です。この電流を、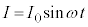 だとします。
だとします。
抵抗両端の電圧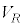 は、オームの法則より、
は、オームの法則より、
コイル両端の電圧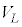 は、
は、
コンデンサー両端の電圧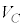 として、公式:
として、公式: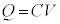 より、
より、
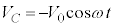 とおくと、
とおくと、
よって、
これより、RLC直列回路の電圧Vは、
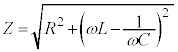 とおくと、δ は、
とおくと、δ は、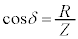 ,
,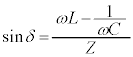 を満たす角。
を満たす角。
これより、電圧Vの実効値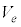 は、電流の実効値を
は、電流の実効値を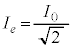 として、
として、
と表され、オームの法則のような関係が成立します。Zは抵抗のような役割をするのですが、これを、RLC回路のインピーダンスと言います。また、δ を電圧と電流の位相のずれと言い、
を満たします。
実は、複素インピーダンスという便利な考え方があります(詳細は、RLC回路の線形2階微分方程式での取扱いを参照)。
回路を流れる電流を複素数として考え、
として、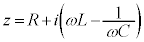 という複素数をかけると、
という複素数をかけると、
として、電流、電圧の実部、虚部を比べることにより、電流と電圧の関係を調べることができます。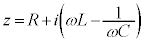 を複素インピーダンスと言います。
を複素インピーダンスと言います。
複素インピーダンスの良いところは、複素インピーダンスを直流におけるオームの法則における抵抗と全く同じようにして、交流を扱えるところにあります。
抵抗Rの複素インピーダンスはRのままです。
自己インダクタンスLのコイルの複素インピーダンスは、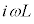 です。
です。
静電容量Cのコンデンサーの複素インピーダンスは、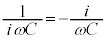 です。
です。
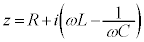 は、R,L,Cのインピーダンスを、抵抗の直列接続のように、3つ加え合わせた合成インピーダンスになっています。
は、R,L,Cのインピーダンスを、抵抗の直列接続のように、3つ加え合わせた合成インピーダンスになっています。
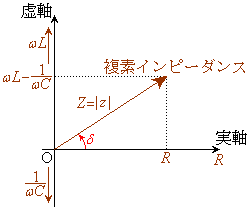 複素数の電流に複素インピーダンスをかけて電圧を求めるということは、右図のように、複素数平面上で、電流を回転・拡大縮小したものが電圧になるということ(極形式を参照)を意味していて、高校物理で言うインピーダンス
複素数の電流に複素インピーダンスをかけて電圧を求めるということは、右図のように、複素数平面上で、電流を回転・拡大縮小したものが電圧になるということ(極形式を参照)を意味していて、高校物理で言うインピーダンス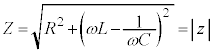 は、回転縮小の比率
は、回転縮小の比率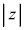 を、電圧が電流より進んでいるとしたときの位相のずれδ は、複素インピーダンスの偏角
を、電圧が電流より進んでいるとしたときの位相のずれδ は、複素インピーダンスの偏角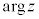 を表しています。
を表しています。
RLC並列回路であれば、合成インピーダンスを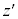 として、
として、
として、抵抗の並列接続のように合成インピーダンスを求めることができます。
虚数単位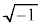 を'i'と書くと、電流を示す'i'と勘違いしやすいので、電気回路の本では、虚数単位を文字'j'で表すことがあります。
を'i'と書くと、電流を示す'i'と勘違いしやすいので、電気回路の本では、虚数単位を文字'j'で表すことがあります。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
物理基礎事項TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 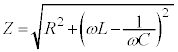
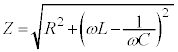
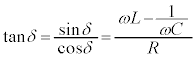
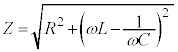 とおくと、δ は、
とおくと、δ は、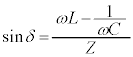 を満たす角。
を満たす角。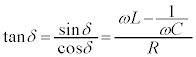
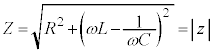 は、回転縮小の比率
は、回転縮小の比率