RLC��H�̐��`2�K�����������ł̎戵���@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
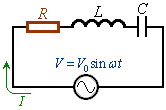 �E�}�̂悤��RLC������H�A�܂�A�𗬓d���ɁA��RR�C���ȃC���_�N�^���XL���R�C���A�Ód�e��C���R���f���T�[��ɐڑ�������H���A���`2�K�����������Ŏ�舵���Č��܂��B
�E�}�̂悤��RLC������H�A�܂�A�𗬓d���ɁA��RR�C���ȃC���_�N�^���XL���R�C���A�Ód�e��C���R���f���T�[��ɐڑ�������H���A���`2�K�����������Ŏ�舵���Č��܂��B
�����ł́AR�CL�CC�͂�����������l���Ƃ�[���ł͂Ȃ��Ƃ��܂��B
��R�A�R�C���A�R���f���T�[�ɂ������d���~���́A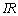 �C
�C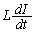 �C
�C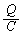 �Ȃ̂ŁA�L���q�z�b�t��2�@�����A�����̑��a���𗬓d�����N�d��V�ɓ������Ƃ����āA
�Ȃ̂ŁA�L���q�z�b�t��2�@�����A�����̑��a���𗬓d�����N�d��V�ɓ������Ƃ����āA
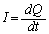 ���A���ӂ�����t�Ŕ�������ƁA
���A���ӂ�����t�Ŕ�������ƁA
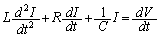 �@����@
�@����@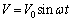 �̂Ƃ��A�@�ɁA
�̂Ƃ��A�@�ɁA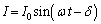 ��������ƁA
��������ƁA
�A���A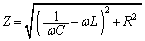 �C
�C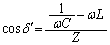 �C
�C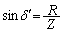
������A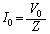 �C
�C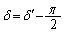 �C�܂�A
�C�܂�A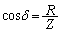 �C
�C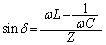 �Ƃ��āA
�Ƃ��āA
�@�̉��́A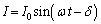 �ŗ^�����܂��B
�ŗ^�����܂��B
�����ŁA�@�����d���Ɠd�����Ɍ`���ŁA
�Ƃ��Ă݂܂��B
������@�ɑ�����āA
���ӂ�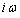 �Ŋ����āA
�Ŋ����āA
������A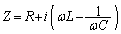 �Ƃ��āA
�Ƃ��āA
���ӂ̐�Βl�ɂ��āA
���ӂ̕Ίp�ɂ��āA
RLC�����H�����������ł����A���ꂪ�A���f�C���s�[�_���XZ���l���闝�R�ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B