���s��w2006�N�O�������������
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
[1]�@���̕���ǂ�ŁA�@�@�ɓK�������܂��͐��l�����ꂼ��̉��ɋL������B
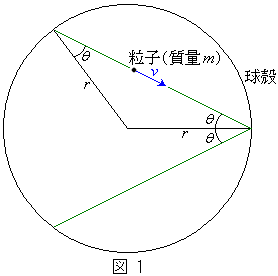 �@�}1�̂悤�ɁA����m�̗��q���A����v�ŁA���ar�̋��k���ʂƒe���Փ˂��J��Ԃ��Ă���B���k�Ƃ̏Փˊp�x��θ (���W�A��)�Ƃ���B
�@�}1�̂悤�ɁA����m�̗��q���A����v�ŁA���ar�̋��k���ʂƒe���Փ˂��J��Ԃ��Ă���B���k�Ƃ̏Փˊp�x��θ (���W�A��)�Ƃ���B
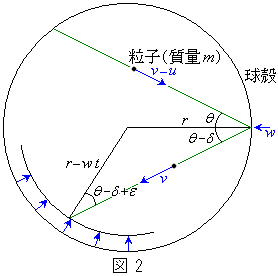
1�̗��q��1��̏Փ˂ŋ��k�ɗ^����͐ς��@�A�@�ł���B��������k�ɏՓ˂��Ă��玟�̏Փ˂���܂ł̎���(��s����)�Ŋ��邱�Ƃɂ��A�P�ʎ��ԓ�����̗͐ς̑��a�@�C�@���^������B����v��N�̗��q���݂��ɏՓ˂��邱�ƂȂ��A���k���ʂ̗l�X�ȏꏊ�ŏՓ˂��J��Ԃ��Ă���Ƃ���B���k�����ϓI�Ɏ鈳��P�́A�P�ʎ��ԓ�����̗͐ς����k�̕\�ʐςŊ������ʂŗ^������B���Ȃ킿�A
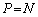 �~�@�E�@�@�@�@(1)
�~�@�E�@�@�@�@(1)
 �@���āA���̋��k�̔��a���������Ək�߂Ă����ߒ����l���悤(�}2)�B���a���k�ޑ���w�͗��q�̑���v�ɔ�ׂď\�����������̂Ƃ���B
�@���āA���̋��k�̔��a���������Ək�߂Ă����ߒ����l���悤(�}2)�B���a���k�ޑ���w�͗��q�̑���v�ɔ�ׂď\�����������̂Ƃ���B
���q������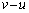 �C�p�xθ �ŁA����w�ŋ߂Â��Ă����(���k)�ɏՓ˂����B���̏Փ˂ɂ���āA���q�̑�����v�ւƑ������A���ˊp�x��
�C�p�xθ �ŁA����w�ŋ߂Â��Ă����(���k)�ɏՓ˂����B���̏Փ˂ɂ���āA���q�̑�����v�ւƑ������A���ˊp�x��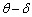 �ւƌ��������B�ǂɐ����ȕ����̉^���ɂ��ẮA����w�ňړ�����ǂ𒆐S�Ɋ��S���˂���̂�
�ւƌ��������B�ǂɐ����ȕ����̉^���ɂ��ẮA����w�ňړ�����ǂ𒆐S�Ɋ��S���˂���̂�
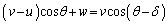 �|�@�G�@�@�@�@(2)
�|�@�G�@�@�@�@(2)
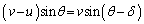 �@�@�@(3)
�@�@�@(3)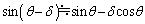 �C�����
�C�����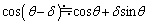 �̊W�����藧�Ƃ��ĊW��(2)��(3)�������ƁA1��̏Փ˂ɂ�鑬�x�̑�����u��(w�Cθ ��p����)�@�I�@�C�p�x�̌�����δ ��(w�Cv�Cθ ��p����)�@�J�@�ŗ^������B
�̊W�����藧�Ƃ��ĊW��(2)��(3)�������ƁA1��̏Փ˂ɂ�鑬�x�̑�����u��(w�Cθ ��p����)�@�I�@�C�p�x�̌�����δ ��(w�Cv�Cθ ��p����)�@�J�@�ŗ^������B
���āA����0 (�[��)�Ŋp�x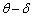 �Ŕ��˂������q�����ɋ��k�ɏՓ˂��鎞��t�ɂ́A���k�̔��a��
�Ŕ��˂������q�����ɋ��k�ɏՓ˂��鎞��t�ɂ́A���k�̔��a��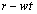 �ɏk�����Ă���B���̔��a�̏k���ɔ����A�Փˊp�x��
�ɏk�����Ă���B���̔��a�̏k���ɔ����A�Փˊp�x��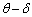 ����ε �������������Ƃ���B�}2����킩��悤��
����ε �������������Ƃ���B�}2����킩��悤��
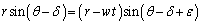 �@�@�@(4)
�@�@�@(4)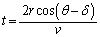 �Ƌߎ�����A���̔�s���Ԃɂ���Đ�����Փˊp�x�̑�����ε ��(w�Cv�Cθ�Cδ ��p����)�@�L�@�ƕ\�����B����ε �́A���a���k�ޑ���w���\���������Ɍ��ł�δ �Ɠ������B�܂�A���k���a���������Ək��������ߒ��ł́A1��̏Փ˂ɂ���Đ������p�x�̌�����δ �͔�s���Ԃɂ���Đ������p�x�̑�����ε �ɂ���đ��E����A�Փˊp�x�͏�Ɉ��ɕۂ����B
�Ƌߎ�����A���̔�s���Ԃɂ���Đ�����Փˊp�x�̑�����ε ��(w�Cv�Cθ�Cδ ��p����)�@�L�@�ƕ\�����B����ε �́A���a���k�ޑ���w���\���������Ɍ��ł�δ �Ɠ������B�܂�A���k���a���������Ək��������ߒ��ł́A1��̏Փ˂ɂ���Đ������p�x�̌�����δ �͔�s���Ԃɂ���Đ������p�x�̑�����ε �ɂ���đ��E����A�Փˊp�x�͏�Ɉ��ɕۂ����B
����A���q�̑����͏Փ˂̂��тɑ�������B�Փ�1����ɑ����������闦�Ɣ��a���k�����闦�̐ς�(w�Cv�Cθ�Cδ ��p����)
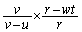 ���@�N�@�@�@�@(5)
���@�N�@�@�@�@(5)
���k�̎鈳�͂́A�P�ʎ��ԓ�����̗͐ς����k�̕\�ʐςŊ������ʂŗ^�����邪�A����͎�(1)�Ō����悤�ɁA���q�̑���v��2��ɔ�Ⴕ�A���ar��3��ɔ���Ⴗ��B��Œ��ׂ��悤�ɁA���k���a���������ω�������ꍇ�ɂ́A���q�̑��������a�ɔ���Ⴗ��̂ŁA����P�͑̐ς��@�P�@��ɔ�Ⴕ�ĕω�����B
[��]
[2]�@���̕���ǂ�ŁA�@�@�ɂ͓K�������܂��͐��l���A{�@�@}����͐��������̂�I�т��̔ԍ����A���ꂼ��̉��ɋL������B
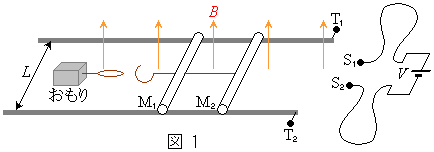
�����Ȕ̏�ɁA�}1�̂悤�ɓ��̂łł����\���ɒ���2�{�̃��[�����ԊuL�ŕ��s�ɒu����Ă���B�d�C��R��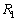 �̋����_
�̋����_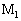 �ƁA�d�C��R��
�ƁA�d�C��R��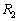 �̋����_
�̋����_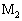 �͂Ƃ��ɒ�����L�ŁA�≏�̂̎��łȂ����2�{�̃��[���ɒ������Ēu����A���̏�����E�ɖ��C�Ȃ�������悤�ɂȂ��Ă���B2�{�̃��[���Ԃɂ͈�l�Ȏ������xB (
�͂Ƃ��ɒ�����L�ŁA�≏�̂̎��łȂ����2�{�̃��[���ɒ������Ēu����A���̏�����E�ɖ��C�Ȃ�������悤�ɂȂ��Ă���B2�{�̃��[���Ԃɂ͈�l�Ȏ������xB (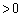 )�̎��E������������ɂ������Ă���B�����_
)�̎��E������������ɂ������Ă���B�����_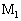 �̒��S�ɂ́A������ƔƂ̖��C�ɂ��A�������ɗ͂������邱�Ƃ��ł���悤�ɂȂ��Ă���B�������A�d�C��R��
�̒��S�ɂ́A������ƔƂ̖��C�ɂ��A�������ɗ͂������邱�Ƃ��ł���悤�ɂȂ��Ă���B�������A�d�C��R��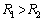 �Ƃ���B�܂��A�����_
�Ƃ���B�܂��A�����_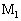 ��
��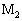 �ȊO�̓��̂̓d�C��R�A����ѓd���ɂ�蔭�����鎥�E�͖����ł�����̂Ƃ���B
�ȊO�̓��̂̓d�C��R�A����ѓd���ɂ�蔭�����鎥�E�͖����ł�����̂Ƃ���B
(1) �d��V�̒����d�������[���ɂȂ��ŋ����_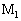 ��
��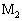 ���E�����ɓ��������߂ɂ́A{�C�@�@�@�[�q
���E�����ɓ��������߂ɂ́A{�C�@�@�@�[�q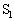 ��[�q
��[�q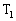 �ɂȂ��A�[�q
�ɂȂ��A�[�q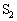 ��[�q
��[�q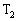 �ɂȂ��C�@�A�@�[�q
�ɂȂ��C�@�A�@�[�q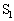 ��[�q
��[�q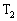 �ɂȂ��A�[�q
�ɂȂ��A�[�q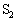 ��[�q
��[�q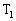 �ɂȂ�}���Ƃ��K�v�ł���B�e�[�q�����̂悤�ɂȂ��œd���𗬂��Ă������_
�ɂȂ�}���Ƃ��K�v�ł���B�e�[�q�����̂悤�ɂȂ��œd���𗬂��Ă������_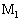 ��
��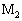 �������Ȃ��悤�ɂ��邽�߂ɂ́A�傫���@���@�̗͂�������ɂ���Ă����Ȃ���Ȃ�Ȃ��B���̂Ƃ������d�����痬��o��d�����@�n�@�ł���B
�������Ȃ��悤�ɂ��邽�߂ɂ́A�傫���@���@�̗͂�������ɂ���Ă����Ȃ���Ȃ�Ȃ��B���̂Ƃ������d�����痬��o��d�����@�n�@�ł���B (2) ��������͂����Ă�����ɂ��͂������Ȃ��悤�ɂ���ƁA�����_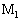 ��
��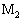 �͉E�����ɓ����o���A���̑����͎���ɑ�������B�����_
�͉E�����ɓ����o���A���̑����͎���ɑ�������B�����_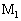 ��
��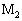 �̑�����u�̂Ƃ��A���E�ɂ���ċ����_
�̑�����u�̂Ƃ��A���E�ɂ���ċ����_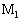 �ɐ�����N�d�͂̑傫�����@�j�@�ł���A�����_
�ɐ�����N�d�͂̑傫�����@�j�@�ł���A�����_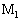 �ɗ����d���̑傫�����@�z�@�ł���B�܂��A�����_
�ɗ����d���̑傫�����@�z�@�ł���B�܂��A�����_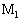 �ɓ����d���͂��@�w�@�ł���B�����_
�ɓ����d���͂��@�w�@�ł���B�����_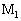 ��
��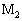 �̎��ʂ��������ꍇ�ɂ́A�����2�̋����_�̉����x�Ƃ��ꂼ��ɓ����͂̊W���l�@���邱�Ƃɂ��A�������_���Ȃ����ɂ��@�g�@�̒��͂������Ă��邱�Ƃ��킩��B���̋����_
�̎��ʂ��������ꍇ�ɂ́A�����2�̋����_�̉����x�Ƃ��ꂼ��ɓ����͂̊W���l�@���邱�Ƃɂ��A�������_���Ȃ����ɂ��@�g�@�̒��͂������Ă��邱�Ƃ��킩��B���̋����_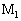 ��
��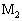 �̓��������͂₪�Ĉ��̒l�@�`�@�ɂȂ�A�����d�����痬��o��d���̑傫�����@���@�ƂȂ�B
�̓��������͂₪�Ĉ��̒l�@�`�@�ɂȂ�A�����d�����痬��o��d���̑傫�����@���@�ƂȂ�B (3) ���ɁA(1)�̏ꍇ�Ƃ͈قȂ邨��������ċ����_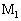 �ɗ�F���������ꍇ���l����B�������A��F�͑O�o���@���@�̗͂������������̂Ƃ���B��Ɠ��l�Ɍ��������ēd���𗬂��A�����_
�ɗ�F���������ꍇ���l����B�������A��F�͑O�o���@���@�̗͂������������̂Ƃ���B��Ɠ��l�Ɍ��������ēd���𗬂��A�����_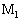 ��
��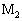 �����������A�₪�Ĉ��̑����ɂȂ����Ƃ��A���̑������@�k�@�ł���B���̂Ƃ������_
�����������A�₪�Ĉ��̑����ɂȂ����Ƃ��A���̑������@�k�@�ł���B���̂Ƃ������_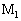 ��
��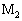 �ɓ����d���͂���F�ɋt����Ă���P�ʎ��Ԃ�����̎d��
�ɓ����d���͂���F�ɋt����Ă���P�ʎ��Ԃ�����̎d��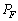 ���@���@�ł���B����A�����_
���@���@�ł���B����A�����_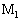 ��
��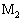 �Ŕ�������W���[���M�̘a
�Ŕ�������W���[���M�̘a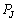 �͒P�ʎ��ԓ������@���@�ł���B�܂��d�����P�ʎ��Ԃ�����ɂ���d��
�͒P�ʎ��ԓ������@���@�ł���B�܂��d�����P�ʎ��Ԃ�����ɂ���d��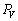 ���@���@�ł���B�������A
���@���@�ł���B�������A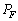 ��
��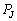 ��
��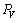 �̊Ԃɂ��@�J�@�̊W�����藧�B
�̊Ԃɂ��@�J�@�̊W�����藧�B [��]
[3]�@���̕���ǂ�ŁA�@�@�ɂ͓K���������A�܂�{�@�@}����͐��������̂�I�т��̔ԍ����A���ꂼ��̉��ɋL������B
(1) ��ʂɔM�̏o�����Ȃ���ԕω���f�M�ω��ƌĂԂ��A�C�̂̒f�M�ω��ł́A�ω��̊e�i�K�ŕ��t��Ԃ��������Ă���Ȃ�A �Ƃ����W�����藧�B�ׂ��萔γ �͋C�̂̎�ނɂ���ĈقȂ邪�A�K��1���傫���l�����B�ȉ��ł́A��C�ɑ���ׂ��萔���Aγ �ƕ\���B
�Ƃ����W�����藧�B�ׂ��萔γ �͋C�̂̎�ނɂ���ĈقȂ邪�A�K��1���傫���l�����B�ȉ��ł́A��C�ɑ���ׂ��萔���Aγ �ƕ\���B ��C�͒f�M�����悢�̂ŁA��C���̋�C�̂������Ƃ����ړ��́A�f�M�ω��Ƃ݂Ȃ����Ƃ��ł���B���܁A���������f�M�ω������肩���������ʁA��C�̈��͂≷�x�́A���x�ɂ���Č��肳��Ă���Ƃ��悤�B�܂��A��C1mol������̎��ʂ�w�Ƃ��A���̒l�͍��x�ɂ�炸���Ƃ���B���̂Ƃ��A�n�\�̋C�����Ή��x��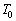 (�ȉ��A���x�͂��ׂĐ�Ή��x�Ƃ���)�C�C�̒萔��R�C�n�\�ɂ������C�̖��x��
(�ȉ��A���x�͂��ׂĐ�Ή��x�Ƃ���)�C�C�̒萔��R�C�n�\�ɂ������C�̖��x��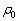 �Ƃ���A�n�\�ɂ������C�̈��͂��@���@�ŗ^������B�܂��A���鍂�x�ɂ������C�̉��x��T�Ƃ���Ƃ��A���̍��x�ł̑�C�̈��͂��@���@�C���x���@���@�ƕ\�����B
�Ƃ���A�n�\�ɂ������C�̈��͂��@���@�ŗ^������B�܂��A���鍂�x�ɂ������C�̉��x��T�Ƃ���Ƃ��A���̍��x�ł̑�C�̈��͂��@���@�C���x���@���@�ƕ\�����B (2) ���āA��C����ɏq�ׂ��悤�ȏ�Ԃɂ���Ƃ��ɁA�M�C���������Ƃ��l���Ă݂悤�B�C���͒f�M���̕z�łł��Ă���A�C�̂̕������������C���̎��ʂ�M�ł���B�ŏ��A�C���͋�C�͓����Ă��Ȃ��̐�0 (�[��)�̏�Ԃł������B��Ȃ��悤�ɋC�����Œ肵�A�C���̉������J������ԂŁA�O�C��M���ĉ��x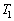 �ɂ�����C��̐��@���@�����l�߂��Ƃ���A�C���͕����юn�߂��B����ɑ����āA���x
�ɂ�����C��̐��@���@�����l�߂��Ƃ���A�C���͕����юn�߂��B����ɑ����āA���x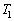 �̋�C���C���̑̐ς�V�ɂȂ�܂œ��ꂽ�B���̂Ƃ��̋C�����̋�C�̕����ʂ��@���@mol�ł���B�܂��A��C�̒�σ�����M��
�̋�C���C���̑̐ς�V�ɂȂ�܂œ��ꂽ�B���̂Ƃ��̋C�����̋�C�̕����ʂ��@���@mol�ł���B�܂��A��C�̒�σ�����M��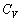 �Ƃ���ƁA�C�����ɓ�������C�ɂ́A���Ƃ̑�C�̏�Ԃ����@���@�̔M���������A�����G�l���M�[���@���@���������������ƂɂȂ�B
�Ƃ���ƁA�C�����ɓ�������C�ɂ́A���Ƃ̑�C�̏�Ԃ����@���@�̔M���������A�����G�l���M�[���@���@���������������ƂɂȂ�B (3) �����ŁA�C���̉�������A�Œ���͂����ċC���������Ƃ���A���鍂�x�܂ŏオ���ĐÎ~�����B�C�����̋�C�̉��x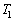 �Ƒ̐�V���ω����Ȃ��Ƃ���ƁA���̍��x�ł̑�C�̉��x���@���@�ł���B����ɁA�C���̉������J���A�̐ς�V�̂܂܋C�����̋�C�̉��x���@���@�ɂ����Ƃ��A�C���̍��x�͕ς��Ȃ������B���̂Ƃ��̋C�����̋�C�̉��x�́A
�Ƒ̐�V���ω����Ȃ��Ƃ���ƁA���̍��x�ł̑�C�̉��x���@���@�ł���B����ɁA�C���̉������J���A�̐ς�V�̂܂܋C�����̋�C�̉��x���@���@�ɂ����Ƃ��A�C���̍��x�͕ς��Ȃ������B���̂Ƃ��̋C�����̋�C�̉��x�́A �B
�B [��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  �B
�B