���啨��'06�N�O��[3]
���̕���ǂ�ŁA�@�@�ɂ͓K���������A�܂�{�@�@}����͐��������̂�I�т��̔ԍ����A���ꂼ��̉��ɋL������B
(1) ��ʂɔM�̏o�����Ȃ���ԕω���f�M�ω��ƌĂԂ��A�C�̂̒f�M�ω��ł́A�ω��̊e�i�K�ŕ��t��Ԃ��������Ă���Ȃ�A �Ƃ����W�����藧�B�ׂ��萔γ �͋C�̂̎�ނɂ���ĈقȂ邪�A�K��1���傫���l�����B�ȉ��ł́A��C�ɑ���ׂ��萔���Aγ �ƕ\���B
�Ƃ����W�����藧�B�ׂ��萔γ �͋C�̂̎�ނɂ���ĈقȂ邪�A�K��1���傫���l�����B�ȉ��ł́A��C�ɑ���ׂ��萔���Aγ �ƕ\���B ��C�͒f�M�����悢�̂ŁA��C���̋�C�̂������Ƃ����ړ��́A�f�M�ω��Ƃ݂Ȃ����Ƃ��ł���B���܁A���������f�M�ω������肩���������ʁA��C�̈��͂≷�x�́A���x�ɂ���Č��肳��Ă���Ƃ��悤�B�܂��A��C1mol������̎��ʂ�w�Ƃ��A���̒l�͍��x�ɂ�炸���Ƃ���B���̂Ƃ��A�n�\�̋C�����Ή��x��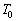 (�ȉ��A���x�͂��ׂĐ�Ή��x�Ƃ���)�C�C�̒萔��R�C�n�\�ɂ������C�̖��x��
(�ȉ��A���x�͂��ׂĐ�Ή��x�Ƃ���)�C�C�̒萔��R�C�n�\�ɂ������C�̖��x��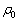 �Ƃ���A�n�\�ɂ������C�̈��͂��@���@�ŗ^������B�܂��A���鍂�x�ɂ������C�̉��x��T�Ƃ���Ƃ��A���̍��x�ł̑�C�̈��͂��@���@�C���x���@���@�ƕ\�����B
�Ƃ���A�n�\�ɂ������C�̈��͂��@���@�ŗ^������B�܂��A���鍂�x�ɂ������C�̉��x��T�Ƃ���Ƃ��A���̍��x�ł̑�C�̈��͂��@���@�C���x���@���@�ƕ\�����B (2) ���āA��C����ɏq�ׂ��悤�ȏ�Ԃɂ���Ƃ��ɁA�M�C���������Ƃ��l���Ă݂悤�B�C���͒f�M���̕z�łł��Ă���A�C�̂̕������������C���̎��ʂ�M�ł���B�ŏ��A�C���͋�C�͓����Ă��Ȃ��̐�0 (�[��)�̏�Ԃł������B��Ȃ��悤�ɋC�����Œ肵�A�C���̉������J������ԂŁA�O�C��M���ĉ��x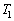 �ɂ�����C��̐��@���@�����l�߂��Ƃ���A�C���͕����юn�߂��B����ɑ����āA���x
�ɂ�����C��̐��@���@�����l�߂��Ƃ���A�C���͕����юn�߂��B����ɑ����āA���x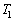 �̋�C���C���̑̐ς�V�ɂȂ�܂œ��ꂽ�B���̂Ƃ��̋C�����̋�C�̕����ʂ��@���@mol�ł���B�܂��A��C�̒�σ�����M��
�̋�C���C���̑̐ς�V�ɂȂ�܂œ��ꂽ�B���̂Ƃ��̋C�����̋�C�̕����ʂ��@���@mol�ł���B�܂��A��C�̒�σ�����M��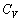 �Ƃ���ƁA�C�����ɓ�������C�ɂ́A���Ƃ̑�C�̏�Ԃ����@���@�̔M���������A�����G�l���M�[���@���@���������������ƂɂȂ�B
�Ƃ���ƁA�C�����ɓ�������C�ɂ́A���Ƃ̑�C�̏�Ԃ����@���@�̔M���������A�����G�l���M�[���@���@���������������ƂɂȂ�B (3) �����ŁA�C���̉�������A�Œ���͂����ċC���������Ƃ���A���鍂�x�܂ŏオ���ĐÎ~�����B�C�����̋�C�̉��x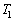 �Ƒ̐�V���ω����Ȃ��Ƃ���ƁA���̍��x�ł̑�C�̉��x���@���@�ł���B����ɁA�C���̉������J���A�̐ς�V�̂܂܋C�����̋�C�̉��x���@���@�ɂ����Ƃ��A�C���̍��x�͕ς��Ȃ������B���̂Ƃ��̋C�����̋�C�̉��x�́A
�Ƒ̐�V���ω����Ȃ��Ƃ���ƁA���̍��x�ł̑�C�̉��x���@���@�ł���B����ɁA�C���̉������J���A�̐ς�V�̂܂܋C�����̋�C�̉��x���@���@�ɂ����Ƃ��A�C���̍��x�͕ς��Ȃ������B���̂Ƃ��̋C�����̋�C�̉��x�́A �B
�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1)(��)�@�n�\�ɂ����đ�Cn[mol]���̐�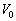 �̋�Ԃɑ��݂������x��
�̋�Ԃɑ��݂������x��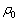 �ɂȂ�Ƃ���ƁA���������ɂ��āA
�ɂȂ�Ƃ���ƁA���������ɂ��āA �� 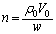 �n�\�ɂ�������C����
�n�\�ɂ�������C����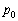 �Ƃ��āA��ԕ������F
�Ƃ��āA��ԕ������F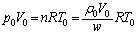 �@����@
�@����@
�� 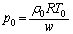 ......[��]�@����A
......[��]�@����A
(��)�@��蕶�́u��C���̋�C�̂������Ƃ����ړ��́A�f�M�ω��Ƃ݂Ȃ����Ƃ��ł���B���܁A���������f�M�ω������肩���������ʁA��C�����������x�́A���x�ɂ���Č��肳��Ă���Ƃ��悤�B�v�Ƃ����\�����ǂ��l���邩�ł����A�d�͉����x���^�����Ă��Ȃ��̂ŁA(���̋C�̂������ɂ����)�{(�n�\�����ɂ���C�̂ɓ����d��)��(�n�\����C���ɂ����)�ƍl���邱�Ƃ͂ł��܂���B �Ƃ������Ƃ́A���̖�蕶���̃q���g���A�n�\�̋C�̂����Ɉړ����āA���̍ہA�f�M�ω������Ƃ��čl����A�Ƃ����q���g�Ƃ��čl���邱�Ƃɂ��܂��B���xT�����x�ɂ������C��������p�C��Cn[mol]���̐���V�C���x��ρ�Ƃ��܂��B�������x�ł̋C�̂���ԕ������F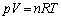
�� 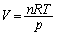 ����@���A
����@���A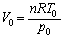
��蕶���ɗ^�����Ă����f�M�ω��ɂ�����A �Ƃ����W(�|�A�b�\���̊W��)��p����ƁA
�Ƃ����W(�|�A�b�\���̊W��)��p����ƁA �� 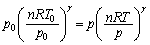 ��
�� 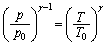 ��
�� 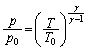 �@����B
�@����B
�A��p���āA 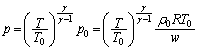 ......[��]
......[��]
(��)�@(��)�����߂��̂Ɠ��l�ɍl���āA
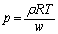 �@����C
�@����C�C���A���A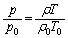
�B���A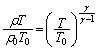
�� 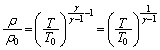 �@����D
�@����D 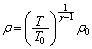 ......[��]
......[��]
(2)(��)�@�C�ɂ����āAR�͒萔�䂦�Ap��w�����̏ꍇ�A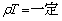 �@���(��) �ł��B
�@���(��) �ł��B �C���������юn�߂��Ƃ��̋C���������x��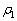 �C�̐���
�C�̐���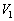 ���Ƃ��܂��B���̂Ƃ��A�C���������J���Ă���̂ŁA�C�̂���������C��
���Ƃ��܂��B���̂Ƃ��A�C���������J���Ă���̂ŁA�C�̂���������C��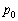 �ł��B(��)���A
�ł��B(��)���A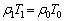
�� 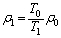 �@����E�@((��)�̌��ʂ͒f�M�ω������Ă���ꍇ�A�E���舳�ω��̏ꍇ)�d�͉����x��g�Ƃ��āA�C���������юn�߂��Ƃ��A�C���ɓ������́A������ɓ�������
�@����E�@((��)�̌��ʂ͒f�M�ω������Ă���ꍇ�A�E���舳�ω��̏ꍇ)�d�͉����x��g�Ƃ��āA�C���������юn�߂��Ƃ��A�C���ɓ������́A������ɓ�������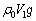 �C�C�̂̕������������C���ɓ����d��
�C�C�̂̕������������C���ɓ����d��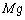 (������)�C�C�����̋C�̂ɓ����d��
(������)�C�C�����̋C�̂ɓ����d��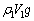 (������)�ł��B
(������)�ł��B
�������͂̂荇��(�C���������яオ��u�Ԃɂ͂܂��͂̂荇�����������Ă��܂�)���A �E���A
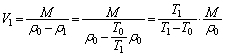 ......[��]
......[��]
(��)�@�C�����̋C�̂��̐���V�ɂȂ����Ƃ�(�C���̉������J���Ă���̂ŁA������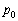 �̂܂�)�A�C�̂̕����ʂ�n[mol]���Ƃ��āA
�̂܂�)�A�C�̂̕����ʂ�n[mol]���Ƃ��āA �C�̂���ԕ������F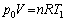
�� 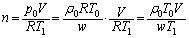 ......[��]
......[��]
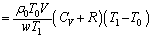 ......[��]
......[��]
(��)�@�����G�l���M�[�̑����́A
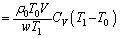 ......[��]
......[��]
(3)(��)�@�C�����̐���V�̂܂܂Ȃ̂ŁA�C�����̋C�̂����x��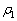 �̂܂܂ł��B�C�����Î~�����Ƃ��A�������x�ł̑�C�����x��ρ�Ƃ��āA�C���ɓ������́A����
�̂܂܂ł��B�C�����Î~�����Ƃ��A�������x�ł̑�C�����x��ρ�Ƃ��āA�C���ɓ������́A����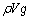 (�����)�C�C�̂̕������������C���ɓ����d��
(�����)�C�C�̂̕������������C���ɓ����d��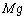 (������)�C�C�����̋C�̂ɓ����d��
(������)�C�C�����̋C�̂ɓ����d��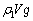 �ł��B
�ł��B �������͂̂荇�����A
�E���A
�� 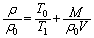 �@����F
�@����F ����C�����Î~�������x�ɂ������C�����x��T�Ƃ���A�D�ƇF���A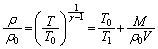
���ӂ�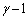 �悵�āA
�悵�āA 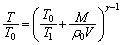 �@����G
�@����G�� 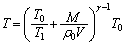 ......[��]
......[��]
(��)�@�C���̉������J���ƋC�����̋C�̂������́A�������x�ł̋C�̂�����p�ɂȂ�܂��B�C�����̋C�̂����x��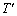 �Ƃ��܂��B�܂��A���̂Ƃ��A�C�̂��̐���V�̂܂܂Ȃ̂ŁA��ϕω��ɂȂ�܂��B
�Ƃ��܂��B�܂��A���̂Ƃ��A�C�̂��̐���V�̂܂܂Ȃ̂ŁA��ϕω��ɂȂ�܂��B �C���̉������J���O�̋C�����̋C�̂������́A�C���̉�����n�\�ŕ����Ƃ�������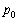 �̂܂܂ł��B�������J���Ă��A�C���ɓ����͂̂荇�����������Ă���̂ŁA�C�����̋C�̗̂ʂ�n[mol]�̂܂ܕω����܂���B�C�����̋C�̂ɂ��āA
�̂܂܂ł��B�������J���Ă��A�C���ɓ����͂̂荇�����������Ă���̂ŁA�C�����̋C�̗̂ʂ�n[mol]�̂܂ܕω����܂���B�C�����̋C�̂ɂ��āA
�������J���O����ԕ������F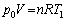 �@����H
�@����H
�������J���������ԕ������F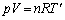 �@����I
�@����I
�I���H���A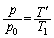 �@����J
�@����J
�B��p���āA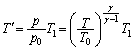
�G��p���āA 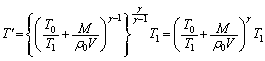 ......[��]
......[��]
(��)�@��ӂ��A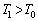 �ł��B
�ł��B �܂��A�C���̌Œ���͂����ċC������яオ�����Ƃ������Ƃ́A
����āA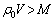
�]���āA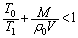 (��)�̌��ʂɂ����āA
(��)�̌��ʂɂ����āA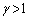 ���A
���A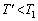
�A ......[��]�@(���̌��ʁA�J���A���ɍs���ق��������������Ȃ邱�Ƃ��킩��܂�)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  �B
�B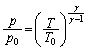 �@����B
�@����B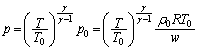 ......[��]
......[��]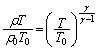
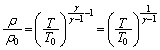 �@����D
�@����D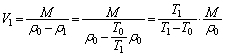 ......[��]
......[��]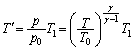
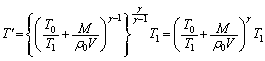 ......[��]
......[��]