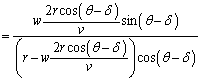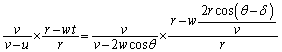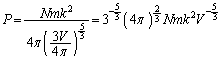京大物理'06年前期[1]
次の文を読んで、 に適した式または数値をそれぞれの解答欄に記入せよ。
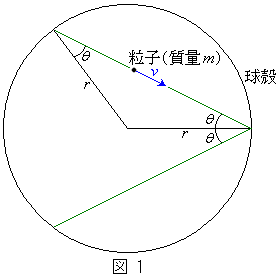 図1のように、質量mの粒子が、速さvで、半径rの球殻内面と弾性衝突を繰り返している。球殻との衝突角度をθ (ラジアン)とする。
図1のように、質量mの粒子が、速さvで、半径rの球殻内面と弾性衝突を繰り返している。球殻との衝突角度をθ (ラジアン)とする。
1つの粒子が1回の衝突で球殻に与える力積は ア である。これを球殻に衝突してから次の衝突するまでの時間(飛行時間)で割ることにより、単位時間当たりの力積の総和 イ が与えられる。速さvのN個の粒子が互いに衝突することなく、球殻内面の様々な場所で衝突を繰り返しているとする。球殻が平均的に受ける圧力Pは、単位時間当たりの力積を球殻の表面積で割った量で与えられる。すなわち、
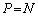 × ウ (1)
× ウ (1)
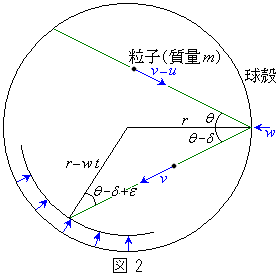 さて、この球殻の半径をゆっくりと縮めていく過程を考えよう(図2)。半径が縮む速さwは粒子の速さvに比べて十分小さいものとする。
さて、この球殻の半径をゆっくりと縮めていく過程を考えよう(図2)。半径が縮む速さwは粒子の速さvに比べて十分小さいものとする。
粒子が速さ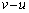 ,角度θ で、速さwで近づいてくる壁(球殻)に衝突した。この衝突によって、粒子の速さはvへと増加し、反射角度は
,角度θ で、速さwで近づいてくる壁(球殻)に衝突した。この衝突によって、粒子の速さはvへと増加し、反射角度は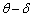 へと減少した。壁に垂直な方向の運動については、速さwで移動する壁を中心に完全反射するので
へと減少した。壁に垂直な方向の運動については、速さwで移動する壁を中心に完全反射するので
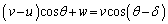 − エ (2)
− エ (2)
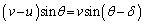 (3)
(3)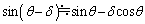 ,および
,および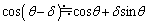 の関係が成り立つとして関係式(2)と(3)を解くと、1回の衝突による速度の増加分uは(w,θ を用いて) オ ,角度の減少分δ は(w,v,θ を用いて) カ で与えられる。
の関係が成り立つとして関係式(2)と(3)を解くと、1回の衝突による速度の増加分uは(w,θ を用いて) オ ,角度の減少分δ は(w,v,θ を用いて) カ で与えられる。
さて、時刻0 (ゼロ)で角度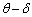 で反射した粒子が次に球殻に衝突する時刻tには、球殻の半径は
で反射した粒子が次に球殻に衝突する時刻tには、球殻の半径は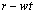 に縮小している。この半径の縮小に伴い、衝突角度は
に縮小している。この半径の縮小に伴い、衝突角度は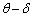 からε だけ増加したとする。図2からわかるように
からε だけ増加したとする。図2からわかるように
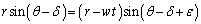 (4)
(4)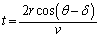 と近似すれば、この飛行時間によって生じる衝突角度の増加分ε は(w,v,θ,δ を用いて) キ と表される。このε は、半径が縮む速さwが十分小さい極限ではδ と等しい。つまり、球殻半径をゆっくりと縮小させる過程では、1回の衝突によって生じた角度の減少分δ は飛行時間によって生じた角度の増加分ε によって相殺され、衝突角度は常に一定に保たれる。
と近似すれば、この飛行時間によって生じる衝突角度の増加分ε は(w,v,θ,δ を用いて) キ と表される。このε は、半径が縮む速さwが十分小さい極限ではδ と等しい。つまり、球殻半径をゆっくりと縮小させる過程では、1回の衝突によって生じた角度の減少分δ は飛行時間によって生じた角度の増加分ε によって相殺され、衝突角度は常に一定に保たれる。
一方、粒子の速さは衝突のたびに増加する。衝突1回当たりに速さが増える率と半径が縮小する率の積は(w,v,θ,δ を用いて)
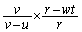 = ク (5)
= ク (5)
球殻の受ける圧力は、単位時間当たりの力積を球殻の表面積で割った量で与えられるが、それは式(1)で見たように、粒子の速さvの2乗に比例し、半径rの3乗に反比例する。上で調べたように、球殻半径をゆっくり変化させる場合には、粒子の速さが半径に反比例するので、圧力Pは体積の ケ 乗に比例して変化する。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 球殻に閉じ込められた気体を題材として、断熱変化における「ポアッソンの関係式: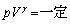 」(この問題では、気体分子を粒子と考えているので、単原子分子理想気体であって、
」(この問題では、気体分子を粒子と考えているので、単原子分子理想気体であって、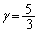 )を求めてみよう、という問題です。なお、理想気体、気体分子運動論を参照してください。
)を求めてみよう、という問題です。なお、理想気体、気体分子運動論を参照してください。
とっつきにくそうな問題ですが、丁寧な誘導がついているので、誘導に従って計算を進めてゆけばゴールにたどりつけます。
(ア) 1個の粒子の衝突前の速度の、衝突面に垂直な成分は、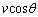
球殻内面と弾性衝突するので、衝突後の速度の衝突面に垂直な成分の大きさは、衝突前と同じで、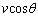
向きは、衝突前と逆向きになるので、衝突後の速度の、衝突面に垂直な成分は、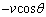
衝突面に対して垂直な方向で、1個の粒子が受ける力積は、運動量の変化に等しく(運動量の原理を参照)、 1個の粒子が1回の衝突で球殻に与える力積は、粒子が受ける力積と等大逆向き(作用・反作用の法則を参照)で、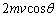 ......[答]
......[答]
(イ) 1個の粒子が球殻内面に衝突してから次に衝突するまでに、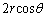 進みます。粒子は、速さvで進むので、球殻内面に衝突してから次に衝突するまでの時間は、
進みます。粒子は、速さvで進むので、球殻内面に衝突してから次に衝突するまでの時間は、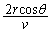
1個の粒子が単位時間に球殻内面に衝突する回数は、1秒を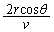 で割って、
で割って、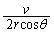 1個の粒子が単位時間に受ける力積の総和は、1回の衝突における力積に回数をかけて、
1個の粒子が単位時間に受ける力積の総和は、1回の衝突における力積に回数をかけて、 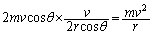 ......[答]
......[答]
(ウ) 球殻内には、N個の粒子がいるので、単位時間に球殻内の全粒子が球殻に与える力積の総和は、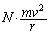
球殻内面の表面積は、半径rの球面の面積として、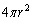
球殻が平均的に受ける圧力Pは、 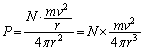 (1)
(1)
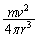 ......[答]
......[答]
(エ) 壁に垂直な方向について、壁の速度はw,粒子の衝突前の速度は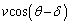 ,衝突後の速度は
,衝突後の速度は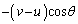 より、粒子は弾性衝突するので、
より、粒子は弾性衝突するので、 w ......[答]
(オ) 壁に平行な方向について、
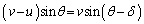 (3)
(3)(2)で、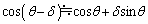 と近似すると、
と近似すると、 ∴ 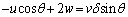 (6)
(6)
(3)で、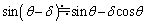 と近似すると、
と近似すると、 ∴ 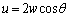 ......[答]
......[答]
(カ) (オ)の結果を(7)に代入すると、
∴ 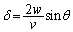 ......[答]
......[答]
(キ) 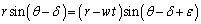 (4)
(4) wはvに比べて十分に小さいので、ε も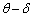 に比べて十分に小さいと考えることができて、
に比べて十分に小さいと考えることができて、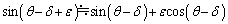 と近似すると、
と近似すると、 ∴ 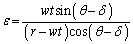
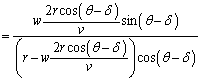
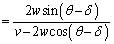 ......[答]
......[答]
(ク) 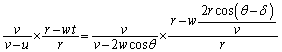
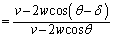 ......[答]
......[答]
(ケ) (ク)は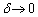 の極限で1に近づくので、
の極限で1に近づくので、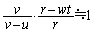 と近似すると、
と近似すると、 速さが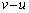 からvに変化するときに、半径はrから
からvに変化するときに、半径はrから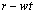 へと変わるので、これは、粒子の速さvが、球殻の半径rに反比例して変化することを意味します。そこで、kを定数として、
へと変わるので、これは、粒子の速さvが、球殻の半径rに反比例して変化することを意味します。そこで、kを定数として、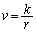 とおくと、(1)より、
とおくと、(1)より、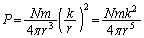
球殻内の体積Vは、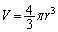 より、
より、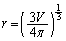 ,これを代入すると、
,これを代入すると、 よって、圧力は体積の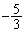 乗に比例します。
乗に比例します。 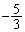 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
京大物理TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 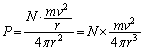 (1)
(1)