���s��w2007�N�O�������������
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
[1]�@���̕���ǂ�ŁA�@�@�ɂ͓K���������A�@�@�ɂ͓K�Ȍ����A{�@�@}�ɂ͐}3��6�̃O���t����K�Ȃ��̂�I�т��̔ԍ����A���ꂼ��̉��ɋL������B�܂��A��1�C��2�ł͎w���ɂ��������āA�����ꂼ��̉��̘g���ɋL������B
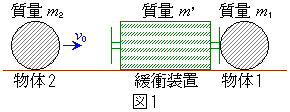 �}1�̂悤�ɁA���炩�Ȗʂ̏�ŐÎ~���Ă��鎿��
�}1�̂悤�ɁA���炩�Ȗʂ̏�ŐÎ~���Ă��鎿��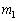 �̕���1�Ɍ������āA����
�̕���1�Ɍ������āA����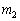 �̕���2������
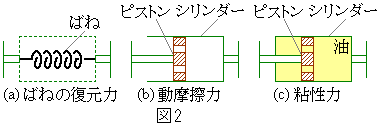
�̕���2������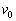 �őł��o�����Ƃ��A�Փ˂ɂ���ĕ���1����Ռ����A�ɏՑ��u�ɂ���Ăǂ̂悤�Ɏ�߂��邩���l����B���̂̑傫���͖����ł��A�^���͐}�̍��E������݂̂Ƃ��A��C��R��ʂ���̖��C�͂͂Ȃ����̂Ƃ���B�ɏՑ��u�̃��f���Ƃ��āA�}2�̂悤��3��ނ��l����B���f��(a)�́A�˒萔K�̂˂ł���B���f��(b)�ł́A���R�ɋ�C���o����ł��錊�̂���s�X�g�����V�����_�[�����A�V�����_�[������̑傫��F�̓����C�͂�����̂Ƃ���B���f��(c)�ł́A���̂���s�X�g�����A���̂܂����V�����_�[�����A�V�����_�[�ɑ��鑊�ΓI�ȑ����ɒ萔C���悶���傫���̔S���͂�����̂Ƃ���B�Փ˂̊ԁA�����̊ɏՑ��u���k�݂����Ă��܂����Ƃ͂Ȃ��Ƃ���B�ȉ��A�ɏՑ��u�̎���
�őł��o�����Ƃ��A�Փ˂ɂ���ĕ���1����Ռ����A�ɏՑ��u�ɂ���Ăǂ̂悤�Ɏ�߂��邩���l����B���̂̑傫���͖����ł��A�^���͐}�̍��E������݂̂Ƃ��A��C��R��ʂ���̖��C�͂͂Ȃ����̂Ƃ���B�ɏՑ��u�̃��f���Ƃ��āA�}2�̂悤��3��ނ��l����B���f��(a)�́A�˒萔K�̂˂ł���B���f��(b)�ł́A���R�ɋ�C���o����ł��錊�̂���s�X�g�����V�����_�[�����A�V�����_�[������̑傫��F�̓����C�͂�����̂Ƃ���B���f��(c)�ł́A���̂���s�X�g�����A���̂܂����V�����_�[�����A�V�����_�[�ɑ��鑊�ΓI�ȑ����ɒ萔C���悶���傫���̔S���͂�����̂Ƃ���B�Փ˂̊ԁA�����̊ɏՑ��u���k�݂����Ă��܂����Ƃ͂Ȃ��Ƃ���B�ȉ��A�ɏՑ��u�̎���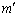 ��
��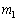 �����
�����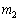 �ɔ�ׂď\�����������̂Ƃ��A�́A���x�A�����x�Ȃǂ̃x�N�g���ʂ́A�}�̉E�����𐳂Ƃ��ĕ\���B
�ɔ�ׂď\�����������̂Ƃ��A�́A���x�A�����x�Ȃǂ̃x�N�g���ʂ́A�}�̉E�����𐳂Ƃ��ĕ\���B
(1) �ɏՑ��u�̉E�[�ƍ��[�����ꂼ�ꕨ��1�ƕ���2�ɂ���ڂ��͂�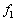 �C
�C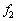 �Ƃ���B�܂��A�ɏՑ��u�̑S����
�Ƃ���B�܂��A�ɏՑ��u�̑S����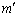 ��
��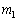 �C
�C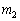 �ɔ�\���ɏ������Ƃ��́A
�ɔ�\���ɏ������Ƃ��́A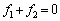 �Ƃ��Ă悢���Ƃ��ȉ��Ŋm�F���Ă������B�@�A�@�̖@�����A�ɏՑ��u������1�ƕ���2�����͂͂��ꂼ��
�Ƃ��Ă悢���Ƃ��ȉ��Ŋm�F���Ă������B�@�A�@�̖@�����A�ɏՑ��u������1�ƕ���2�����͂͂��ꂼ��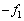 �C
�C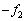 �ł���B����ĊɏՑ��u����O�̘͂a��
�ł���B����ĊɏՑ��u����O�̘͂a��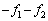 �ł���A����͊ɏՑ��u�̏d�S�̉����x���@�C�@�����������̂ɓ������B�ɏՑ��u�̏d�S�̉����x�͕���1�╨��2�̉����x�Ɠ����x�̑傫���ł���̂ŁA
�ł���A����͊ɏՑ��u�̏d�S�̉����x���@�C�@�����������̂ɓ������B�ɏՑ��u�̏d�S�̉����x�͕���1�╨��2�̉����x�Ɠ����x�̑傫���ł���̂ŁA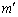 ��
��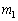 �����
�����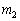 �ɔ�ׂď\���������Ƃ��A
�ɔ�ׂď\���������Ƃ��A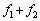 ��
��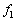 �����
�����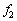 �ɔ�ׂĖ������Ă悢�̂ł���B
�ɔ�ׂĖ������Ă悢�̂ł���B
(2) ���ɁA����1�ƕ���2�̑��Ή^���ɂ��čl����B(1)�Ŋm�F�������Ƃ��A����1�ƕ���2�̉����x��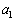 �C
�C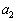 �Ƃ��A
�Ƃ��A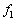 ��f�Ƃ����ƁA�^���������͂��ꂼ��
��f�Ƃ����ƁA�^���������͂��ꂼ��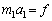 �C
�C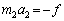 �Ə�����B����2�̎��̗��ӂ����ꂼ��
�Ə�����B����2�̎��̗��ӂ����ꂼ��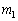 �C
�C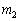 �Ŋ���A�����̍����Ƃ�ƁA
�Ŋ���A�����̍����Ƃ�ƁA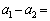 �@�E�@�ƂȂ�B���̎��́A
�@�E�@�ƂȂ�B���̎��́A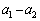 ������2�ɑ��镨��1�̑��Ή^���̉����xa�ł��邱�Ƃɒ��ӂ���ƁA
������2�ɑ��镨��1�̑��Ή^���̉����xa�ł��邱�Ƃɒ��ӂ���ƁA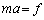 �Ƃ����`�ɏ�����B�����ŁAm�͊��Z���ʂƌĂ�A
�Ƃ����`�ɏ�����B�����ŁAm�͊��Z���ʂƌĂ�A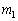 ��
��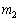 �ɂ���@�G�@�ƕ\�����B���Ȃ킿�A���ʂ�
�ɂ���@�G�@�ƕ\�����B���Ȃ킿�A���ʂ�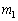 ��
��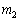 ��2�̕��̂̑��Ή^���́A���ʂ�m��1�̕��̂̉^���Ɠ����������ɂ��������B
��2�̕��̂̑��Ή^���́A���ʂ�m��1�̕��̂̉^���Ɠ����������ɂ��������B
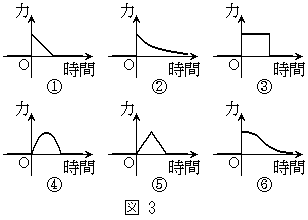 (3)�@�ȏ�̂��Ƃ���A���f��(a)�C(b)�C(c)�̊e�ꍇ�ɕ���1����͂����Ԃ̊��Ƃ��ăO���t�Ɏ����ƁA���ꂼ��}3��{�@�I�@}�C{�@�J�@}�C{�@�L�@}�ƂȂ�B���f��(a)�C(b)�C(c)�̊e�ꍇ�ɁA����1���͂��Ă��鎞�Ԃ͂��ꂼ���@�N�@�C�@�P�@�C������ł���A�͂̍ő�l�͂��ꂼ���@�R�@�C�@�T�@�C�@�V�@�ł���B(�@�N�@�`�@�V�@�ł�m��p���Ă��悢�B�K�v�Ȃ�A���̂����x�ɔ�Ⴕ���x�Ƌt�����̗͂���ꍇ�A���x�̐�Βl�͎��ԂƂƂ��Ɏw�����I�Ɍ������邱�Ƃ�p����B)
(3)�@�ȏ�̂��Ƃ���A���f��(a)�C(b)�C(c)�̊e�ꍇ�ɕ���1����͂����Ԃ̊��Ƃ��ăO���t�Ɏ����ƁA���ꂼ��}3��{�@�I�@}�C{�@�J�@}�C{�@�L�@}�ƂȂ�B���f��(a)�C(b)�C(c)�̊e�ꍇ�ɁA����1���͂��Ă��鎞�Ԃ͂��ꂼ���@�N�@�C�@�P�@�C������ł���A�͂̍ő�l�͂��ꂼ���@�R�@�C�@�T�@�C�@�V�@�ł���B(�@�N�@�`�@�V�@�ł�m��p���Ă��悢�B�K�v�Ȃ�A���̂����x�ɔ�Ⴕ���x�Ƌt�����̗͂���ꍇ�A���x�̐�Βl�͎��ԂƂƂ��Ɏw�����I�Ɍ������邱�Ƃ�p����B)
��1�@���f��(a)�̏ꍇ�A�Փˌ�\���Ȏ��Ԃ����������Ƃ̕���1�̑��x�́A�˒萔K�Ɉˑ����Ȃ��B���̗��R���Ȍ��ɏq�ׂ�B
��2�@�Î~���Ă��鎩���Ԃɕʂ̎����Ԃ��Ǔ˂����B��q�͍K�������ł��������A�����Ԃ�2��Ƃ����Ȃ�Ԃ�Ă��܂����B���̂Ƃ��A�Î~���Ă��������Ԃ̏�q���Փ˂ɂ���Ċ�����A���������̉����x�̍ő�l�͂����炩�B�ɂ�����ߒ���������������ŁA�L������2�����ʼn���B�����Ԃ̎��ʂ͂������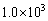 kg�C�Ǔ˂��������Ԃ̏����͎���18km�ł���A2��̎����Ԃ͏Փ˕������Ԃ��25cm���Z���Ȃ����B�Ԃꂽ�������ɏՑ��u�Ƃ݂Ȃ��A���f��(b)�ʼn�͂���B2��Ƃ��u���[�L�������Ă��炸�A�n�ʂƂ̖��C�͖����ł��A�܂��A�����Ԃ̂Ԃꂽ��������я�q�̎��ʂ͖����ł���Ƃ���B
kg�C�Ǔ˂��������Ԃ̏����͎���18km�ł���A2��̎����Ԃ͏Փ˕������Ԃ��25cm���Z���Ȃ����B�Ԃꂽ�������ɏՑ��u�Ƃ݂Ȃ��A���f��(b)�ʼn�͂���B2��Ƃ��u���[�L�������Ă��炸�A�n�ʂƂ̖��C�͖����ł��A�܂��A�����Ԃ̂Ԃꂽ��������я�q�̎��ʂ͖����ł���Ƃ���B [��]
[2]�@���̕���ǂ�ŁA�������@�@�ɓK���������A���ꂼ��̉��ɋL������B�܂��A��1�ł͎w���ɂ��������ď���̉��ɋL������B
�����X�����A���~�j�E���̏�Ŋ��点��ƁA�͊w�I���C�������ł���ꍇ�ł��A���̊��藎���鑬���͒Z���Ԃ̂����ɂقڈ��l�ɒB����B����́A���̉^���ɂƂ��Ȃ��ăA���~�j�E���̓����ɂ����d���������A���̂����d�����玥���͂��邽�߂ɋN���錻�ۂł���B�ȉ��̑��u�́A���̌��ۂ����f�����������̂ł���B
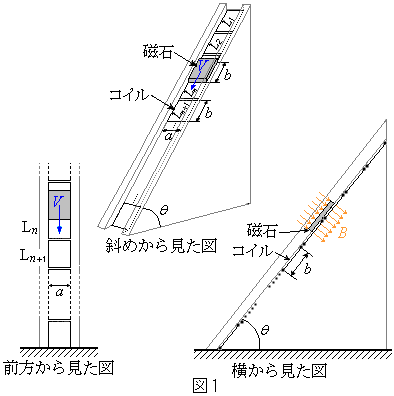 �}1�̂悤�ɁA�����ʂɑ��p�xθ �ŌX������������̃v���X�`�b�N�̔̏ォ��A����m�̎������点��B���̑傫���͕�a�C����b�ŁA���݂͔������̂Ƃ���B�܂����̐^���ɂ͎��̒�ʂɐ����������̋�����l�Ȏ������xB�������Ă���A���̑��̈ʒu�ւ̎������x�͂����ł͍l�����Ȃ����Ƃɂ���B�ɂ͎����Ȃ߂炩�Ɋ���悤�ȕ�a�̍a������A�a�̒�ʂɂ͕�a�C����b�C�d�C��RR�̒����`�̕����d��(�ꊪ���̃R�C��)
�}1�̂悤�ɁA�����ʂɑ��p�xθ �ŌX������������̃v���X�`�b�N�̔̏ォ��A����m�̎������点��B���̑傫���͕�a�C����b�ŁA���݂͔������̂Ƃ���B�܂����̐^���ɂ͎��̒�ʂɐ����������̋�����l�Ȏ������xB�������Ă���A���̑��̈ʒu�ւ̎������x�͂����ł͍l�����Ȃ����Ƃɂ���B�ɂ͎����Ȃ߂炩�Ɋ���悤�ȕ�a�̍a������A�a�̒�ʂɂ͕�a�C����b�C�d�C��RR�̒����`�̕����d��(�ꊪ���̃R�C��)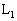 �C
�C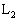 �C����C
�C����C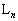 �C
�C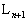 �C������A���݂��d�C�I�ɐ≏����Ă����ԂȂ��������ߍ��܂�Ă���B�d���̑����͖����ł�����̂Ƃ��A�܂��R�C���Ԃ̑��݃C���_�N�^���X�͖����ł��A�R�C���̎��ȃC���_�N�^���X���\���ɏ������A�U���N�d�͂ɉ����ēd���͏\�������ω�������̂Ƃ���B�d�͉����x��g�Ƃ��A���ƔƂ̊Ԃ̖��C�͂���ы�C��R�͖����ł�����̂Ƃ���B
�C������A���݂��d�C�I�ɐ≏����Ă����ԂȂ��������ߍ��܂�Ă���B�d���̑����͖����ł�����̂Ƃ��A�܂��R�C���Ԃ̑��݃C���_�N�^���X�͖����ł��A�R�C���̎��ȃC���_�N�^���X���\���ɏ������A�U���N�d�͂ɉ����ēd���͏\�������ω�������̂Ƃ���B�d�͉����x��g�Ƃ��A���ƔƂ̊Ԃ̖��C�͂���ы�C��R�͖����ł�����̂Ƃ���B
���̏ł́A����o���Ĉ�莞�Ԃ̌�ɂ́A���̉^���́A�ߎ��I�ɓ����x�^���ɂȂ�B���̂Ƃ��̑��x���I�[���x�Ƃ����B
(1) �܂��A��������V�̏I�[���x�ʼn^������ꍇ���l����B
�ォ��n�Ԗڂ̃R�C��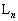 �̏�[�Ɏ����B����������
�̏�[�Ɏ����B����������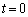 �Ƃ��A�������ɑ�����������t�Ƃ���B���̂Ƃ��A�R�C��
�Ƃ��A�������ɑ�����������t�Ƃ���B���̂Ƃ��A�R�C��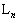 ���т������́A
���т������́A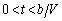 �̂Ƃ�
�̂Ƃ�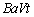 �C
�C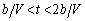 �̂Ƃ��@�C�@�C���̑��̎����ł�0�ƂȂ�B�R�C��
�̂Ƃ��@�C�@�C���̑��̎����ł�0�ƂȂ�B�R�C��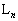 �ɗU�������d���́A�ォ�猩�Ď��v���𐳕����ɂƂ�ƁA
�ɗU�������d���́A�ォ�猩�Ď��v���𐳕����ɂƂ�ƁA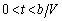 �̂Ƃ��@���@�ƂȂ�A
�̂Ƃ��@���@�ƂȂ�A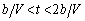 �̂Ƃ��@�n�@�ƂȂ�B���������āA�����R�C��
�̂Ƃ��@�n�@�ƂȂ�B���������āA�����R�C��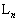 �ɂ���ڂ��͂́A�X�����̕\�ʂɉ����ĉ������𐳂ɂƂ�ƁA
�ɂ���ڂ��͂́A�X�����̕\�ʂɉ����ĉ������𐳂ɂƂ�ƁA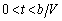 �̂Ƃ��@�j�@�ł���A
�̂Ƃ��@�j�@�ł���A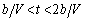 �̂Ƃ��@�z�@�ł���B
�̂Ƃ��@�z�@�ł���B
���̂��Ƃ���A���ׂẴR�C�����玥�����F�́A�Ζʂɕ��s�ɉ������𐳂Ɏ��ƁA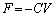 �ƕ\�����Ƃ��ł��A
�ƕ\�����Ƃ��ł��A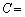 �@�w�@�ƂȂ�B���ɓ����d�͂��l������ƁA������
�@�w�@�ƂȂ�B���ɓ����d�͂��l������ƁA������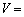 �@�g�@�Ƌ��߂���B(�@�w�@���@�g�@��F�CC�CV��p�����ɕ\���B)
�@�g�@�Ƌ��߂���B(�@�w�@���@�g�@��F�CC�CV��p�����ɕ\���B)
(2) ���ɁA����Î~��Ԃ���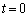 �ŐÂ��ɗ�������A���x���I�[���x(�傫��V)�ɋ߂Â��l�q���l����B((1)�̏ꍇ�Ƃ͎����̌��_���قȂ邱�Ƃɒ��ӂ���B)
�ŐÂ��ɗ�������A���x���I�[���x(�傫��V)�ɋ߂Â��l�q���l����B((1)�̏ꍇ�Ƃ͎����̌��_���قȂ邱�Ƃɒ��ӂ���B) ����t�ɂ����鎥�̑�����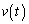 �Ƃ���ƁA(1)�̏ꍇ�Ɠ��l�ɁA�R�C�����玥�����F�́A
�Ƃ���ƁA(1)�̏ꍇ�Ɠ��l�ɁA�R�C�����玥�����F�́A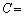 �@�w�@��p���āA
�@�w�@��p���āA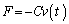 �ƕ\�����Ƃ��ł���B(F�����
�ƕ\�����Ƃ��ł���B(F�����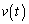 �́A�Ζʂɕ��s�ɉ������𐳂ɂƂ���̂Ƃ���B)���������āA��������
�́A�Ζʂɕ��s�ɉ������𐳂ɂƂ���̂Ƃ���B)���������āA��������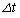 ��p���āAt����
��p���āAt����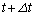 �܂ł̕��ω����x��
�܂ł̕��ω����x��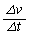 �ŕ\���ƁA���Ɋւ���^����������
�ŕ\���ƁA���Ɋւ���^����������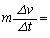 �@�`�@�Ə�����B(�@�`�@��C���܂ގ��ŕ\���B)������V��
�@�`�@�Ə�����B(�@�`�@��C���܂ގ��ŕ\���B)������V��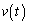 �Ƃ̍��ɒ��ڂ�
�Ƃ̍��ɒ��ڂ�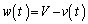 �Ƃ����ƁA���̉^�����������A
�Ƃ����ƁA���̉^�����������A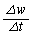 ��w�ɔ�Ⴕ�A
��w�ɔ�Ⴕ�A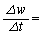 �@���@w�Ə����\����B(�@���@��m��C��p���ĕ\���B)���̕������Ɠ��l�̎��ŕ\����錻�ۂ̈�Ɍ��q�j�̕�����B���q�j�̕���ɂ����ẮA����t�ɂ����錴�q�j�̌���
�@���@w�Ə����\����B(�@���@��m��C��p���ĕ\���B)���̕������Ɠ��l�̎��ŕ\����錻�ۂ̈�Ɍ��q�j�̕�����B���q�j�̕���ɂ����ẮA����t�ɂ����錴�q�j�̌���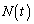 �Ƃ���ƁA�\���ɒZ������
�Ƃ���ƁA�\���ɒZ������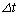 �̊Ԃ̕ω���
�̊Ԃ̕ω���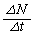 ��
��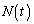 �ɔ�Ⴕ�A���̌W��β ��p����
�ɔ�Ⴕ�A���̌W��β ��p����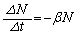 �ƕ\����B���̂悤��
�ƕ\����B���̂悤��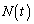 �́A
�́A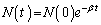 �Ə����邱�Ƃ��m���Ă���B(
�Ə����邱�Ƃ��m���Ă���B(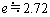 �͎��R�ΐ��̒�ł���B)���������āA
�͎��R�ΐ��̒�ł���B)���������āA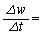 �@���@w����A
�@���@w����A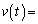 �@�k�@�Ƌ��߂���B(�@�k�@��C���܂ގ��ŕ\���B)���ɁA�����ǂ̂悤�ɏI�[���x�ɋ߂Â��Ă��������l����B�܂��A
�@�k�@�Ƌ��߂���B(�@�k�@��C���܂ގ��ŕ\���B)���ɁA�����ǂ̂悤�ɏI�[���x�ɋ߂Â��Ă��������l����B�܂��A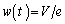 �C���Ȃ킿�A
�C���Ȃ킿�A �ƂȂ鎞��
�ƂȂ鎞��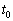 ���l����ƁAm��C��p���āA
���l����ƁAm��C��p���āA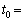 �@���@�ƕ\�����B����
�@���@�ƕ\�����B����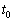 ���ɘa���ԂƂ����B
���ɘa���ԂƂ����B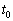 ��p����ƁA
��p����ƁA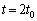 �ł�
�ł�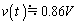 �C
�C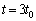 �ł�
�ł�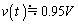 �ƂȂ�A���̉^��������V�̓����x�^���ɋ߂Â��Ă������Ƃ��킩��B
�ƂȂ�A���̉^��������V�̓����x�^���ɋ߂Â��Ă������Ƃ��킩��B
��1�@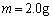 �C
�C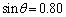 �C
�C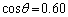 �C
�C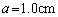 �C
�C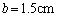 �C
�C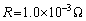 �C
�C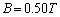 �C
�C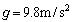 �̏ꍇ�ɂ��āA(a) �I�[���x�̑傫��V�C����сA(b) �ɘa����
�̏ꍇ�ɂ��āA(a) �I�[���x�̑傫��V�C����сA(b) �ɘa����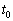 ���v�Z���A�����̒l���A�L������2�����ŒP�ʂ����āA���ꂼ�ꏊ��̉�(a)�C(b)�ɋL������B
���v�Z���A�����̒l���A�L������2�����ŒP�ʂ����āA���ꂼ�ꏊ��̉�(a)�C(b)�ɋL������B [��]
[3]�@���̕���ǂ�ŁA�@�@�ɂ͓K���������A{�@�@}�ɂ͐������ԍ�����I�сA���ꂼ��̉��ɋL������B�܂���1�C��2�C��3�ɂ͓K�Ȑ���������̘g���ɋL�����邱�ƁB
�M�͊w�͋C�̂����ł͂Ȃ��A���܂��܂ȑΏۂɂ��K�p���邱�Ƃ��ł���B�{��ł͂Ђ���̕��̂̔M�͊w���l���Ă݂悤�B����Ђ���̕��̂������L���A������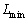 ����
����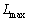 �͈͓̔��Œ���X�𑪒肵���Ƃ���AX�͒���L�Ɉˑ������A��Ή��xT����ѐ��̒萔A��p����
�͈͓̔��Œ���X�𑪒肵���Ƃ���AX�͒���L�Ɉˑ������A��Ή��xT����ѐ��̒萔A��p����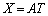 �ƕ\���ꂽ�B���̕��̂̕ό`�Ƃ��ẮAL��
�ƕ\���ꂽ�B���̕��̂̕ό`�Ƃ��ẮAL��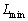 ����
����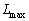 �͈͓̔��ɂ���ꎟ���I�ȐL�k�݂̂��l���A�܂������G�l���M�[U�͐��̒萔C��p����
�͈͓̔��ɂ���ꎟ���I�ȐL�k�݂̂��l���A�܂������G�l���M�[U�͐��̒萔C��p����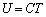 �ƂȂ�Ƃ��āA�ȉ��̖₢�ɓ�����B
�ƂȂ�Ƃ��āA�ȉ��̖₢�ɓ�����B
(1) ���̕��̂ɊO��������d��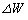 �������Ĕ�����
�������Ĕ�����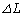 �����L�����Ƃ��ɁA
�����L�����Ƃ��ɁA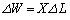 �Ƃ����W�������藧�B�z�M�ʂ�
�Ƃ����W�������藧�B�z�M�ʂ�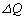 �C�����G�l���M�[�̕ω���
�C�����G�l���M�[�̕ω���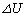 �Ƃ����Ƃ��A�M�͊w���@�����
�Ƃ����Ƃ��A�M�͊w���@�����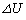 �́A
�́A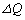 �CA�CT�C
�CA�CT�C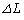 ��p����
��p����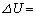 �@���@�ƕ\�����B���
�@���@�ƕ\�����B���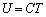 ���A���̂�L�����Ƃ��̉��x�ω�
���A���̂�L�����Ƃ��̉��x�ω� ��p���āA�����G�l���M�[�̕ω���
��p���āA�����G�l���M�[�̕ω���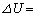 �@���@�Ƃ�������B
�@���@�Ƃ�������B �f�M�I�ɕ��̂��������Ɣ�����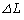 �L�����Ƃ��̉��x�ω�
�L�����Ƃ��̉��x�ω�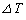 �́AC�CA�CT�C
�́AC�CA�CT�C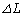 ��p���ĕ\�����@���@�ƂȂ�A���x��{���F�@ ���~����B�@�A �ς��Ȃ��B�@�B �㏸����B}�������A
��p���ĕ\�����@���@�ƂȂ�A���x��{���F�@ ���~����B�@�A �ς��Ȃ��B�@�B �㏸����B}�������A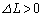 �Ƃ���B
�Ƃ���B
(2) ���āA���̕��̂�f�M�I�ɂ������ƐL�����B���̂Ƃ�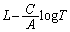 �����ł������B�����ŁA
�����ł������B�����ŁA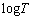 ��T�̎��R�ΐ��ł���B
��T�̎��R�ΐ��ł���B
��1�@���̗��R���q�ׂ�B�������A���̕ϐ�T��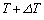 �܂ł킸���ɕω��������Ƃ���
�܂ł킸���ɕω��������Ƃ���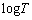 �̕ω��ʂ�
�̕ω��ʂ�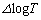 �ƕ\���ƁA
�ƕ\���ƁA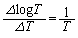 �����藧���Ƃ�p���Ă悢�B
�����藧���Ƃ�p���Ă悢�B
(3) ���ɁA�������̂����xT�ɕۂ����܂܁A����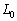 ����L�܂ł������ƕω��������Ƃ��ɕ��̂ɊO���������ꂽ�d�����@���@�ł���A���̊Ԃ̋z�M�ʂ��@���@�ł���B�������A�@���@������@���@��A�CT�C
����L�܂ł������ƕω��������Ƃ��ɕ��̂ɊO���������ꂽ�d�����@���@�ł���A���̊Ԃ̋z�M�ʂ��@���@�ł���B�������A�@���@������@���@��A�CT�C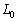 �CL�݂̂ŕ\�����ƁB
�CL�݂̂ŕ\�����ƁB
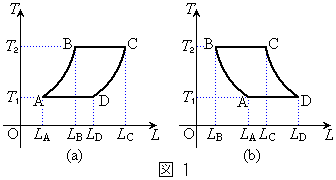 (4) �}1�̂悤�ɉ����̂̒���L�Ƃ��A�c�������xT�Ƃ��Ă��̕��̂̏�ԕω���\���B���̂����x
(4) �}1�̂悤�ɉ����̂̒���L�Ƃ��A�c�������xT�Ƃ��Ă��̕��̂̏�ԕω���\���B���̂����x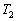 �ɕۂ��������Ɠ����ω��������A���̌��������
�ɕۂ��������Ɠ����ω��������A���̌��������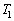 �܂Œf�M�ω������A����ɉ��x
�܂Œf�M�ω������A����ɉ��x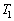 �ł������Ɠ����ω�����������ɁA�f�M�I�ɂ������Ɖ��x
�ł������Ɠ����ω�����������ɁA�f�M�I�ɂ������Ɖ��x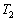 �̏��߂̏�Ԃɖ߂��T�C�N�����l���悤�B�����M��(���x
�̏��߂̏�Ԃɖ߂��T�C�N�����l���悤�B�����M��(���x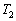 )����M���z�����Ďd�������A�ቷ�M��(���x
)����M���z�����Ďd�������A�ቷ�M��(���x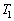 )�ɔM����o����悤�ȃT�C�N���́A{���F�@ (a)�����v���ɉ��B�@�A (a)���v���ɉ��B�@�B (b)�����v���ɉ��B�@�C (b)���v���ɉ��B}
)�ɔM����o����悤�ȃT�C�N���́A{���F�@ (a)�����v���ɉ��B�@�A (a)���v���ɉ��B�@�B (b)�����v���ɉ��B�@�C (b)���v���ɉ��B}
��2�@���̃T�C�N���ł́A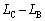 ��
��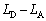 ���������Ȃ�B���̗��R���q�ׂ�B
���������Ȃ�B���̗��R���q�ׂ�B
(5) ��ʂɃT�C�N���ł̔M�����́A���̂��T�C�N����ʂ��ĊO�ɂ��鐳���̎d�����A�����M������z������M��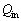 �Ŋ������ʂƂ��ē��������B����āA�T�C�N�������Ԃ̔M�����́A
�Ŋ������ʂƂ��ē��������B����āA�T�C�N�������Ԃ̔M�����́A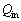 �ƃT�C�N�������Ԃɕ��o����M��
�ƃT�C�N�������Ԃɕ��o����M��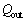 ��p�����@���@�Ə�����B
��p�����@���@�Ə�����B
��3�@����܂ł̌��ʂ�p���āA(4)�̃T�C�N���̔M������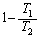 �ƂȂ闝�R���������B
�ƂȂ闝�R���������B [��]
�e�⌟��
[1](��������)�@�債�����̂悤�ɂ͌����Ȃ��̂ł����A�ו����C�ɂ��o���ƁA�Ȃ��Ȃ��Ӓn���ɂł��Ă�����Ȃ̂ŁA������ō��o���ăn�}���Ă��܂��Ղ����ł��B��{�ɒ����ɍl���Ă����Ή��ł��Ȃ����Ƃł����Ă��A��{���痣��Ă��܂��ƁA�~�X���Ղ��Ȃ�܂��B�{��̂悤�Ȗ��ł́A�����������ɂȂ�Ȃ�قǁA���ȏ��ɏ�����Ă����{�I�ȕ����@���ɑ����čl����悤�ɓw�͂��ė~�����Ǝv���܂��B
���́A(3)��(�I)�`(�V)�ł����A�O���t�́A���܂�[���Nj������ɁA(�I)�́A�˂̒P�U��������C�C(�J)�́A���̓����C�͂���������B�C(�L)�́A��蕶�Ɂu���̂����x�ɔ�Ⴕ���x�Ƌt�����̗͂���ꍇ�A���x�̐�Βl�͎��ԂƂƂ��Ɏw�����I�Ɍ�������v�Ƃ����q���g������̂ŇA�C�ƒ����I�ɉ��Ă��܂��̂��悢�����m��܂���B���Ƃ́A�O���t�����Ȃ���l���āA�P�U���̎����ƐU�����l���A�������x�^���̌�����K�p����Γ������o�܂��B
��2�́A�u��q���Փ˂ɂ���Ċ�����A���������̉����x�̍ő�l�v�����߂�A�Ƃ������ƂȂ̂ŁA��蕶������v�����Ă���̂��A��������ƍl���Ă������K�v������܂��B�������������x�^���̖��Ȃ̂ł����A�������Ď��n�̃e�[�}���ނɂ���ƁA���ɂ͓�������邩���m��܂���B
�悭�A����]�_�Ƃ��A��w�����͊���̋�_�������ɂ��Ă��āA�����I�ȃe�[�}������Ȃ��A�ƁA�C�����ᔻ����̂ł����A�����������Ŏ��g�߂�悤�ȃ��x���̖��ɂ��邽�߂ɂ́A���ɂ��낢��Ȑ�������Ȃ�������Ȃ��̂ŁA�ǂ����Ă�����̋�_�ɂȂ��Ă��܂��̂ł��B���������Ӗ��ł́A���n�ɑ��������͋C���o�����߂ɁA���̖��̏o��҂������Ƌ�J���č���Ă���悤�Ɏv���܂��B
[2](��������)�@����'07�N�O��[2]�Ɨގ��̃e�[�}�̖��ł����A����ł́A�G�l���M�[�ۑ�����I�[���x�����߂�̂ɑ��A����ł͔������������l���ďI�[���x�Ɏ��鎞�ԕω��̎������߂�悤�ɂȂ��Ă��܂��B
�ł����A�{������I�z�����Ȃ���Ă���ǖ�̂͂����A���ς�����邽�߂ɁA����Ȃ킩��ɂ����������ɂȂ��Ă��܂��̂ł���A���������������Z�͈̔͂ɓ���Ă��܂��āA�����ƕ��ՂȖ�肷��ׂ����A�ƁA���͎v���܂��B
��ʓI�Ɉ��킸�ɒ萫�I�Ɉ������Ƃɂ���č��Z���ɂ킩��₷���Ȃ�A�Ƌ��d�Ɏ咣�Ȃ���������܂����A���́A�萫�I�ȗ������������邱�Ƃ����Z���̕���������N�����������Ǝv���Ă��܂��B���ς̌v�Z�ōς܂��Ă��܂��ΊȒP�Ȃ��ƂȂ̂ɁA�Ȃ��A���ۓI�ɁA������Ă��܂��̂ł��傤���H
���̖��̑O���́A�����̕ω�����d���A�͂����߂�W���I�Ȗ��ł��B�㔼�́A�����I�ɁA
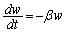 �@����@
�@����@
�Ƃ�����������������A���q�j�̎��R����Ƃ̗ގ������A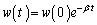 �����e�ɂȂ��Ă��܂��B�ł����A����������������邽�߂ɂ������Ă킩��ɂ������ɂȂ��Ă��܂��Ă��܂��B���l�̖��̓R�̎��^��H���e�[�}�Ƃ���'92�����嗝[3]�Ȃǂɂ�������̂ł����A�j���[�g���ȗ��A�����w�͔��ϕ��w�Ɩ��ڂȊW�ɂ���킯�ŁA�����ɁA�����Ɣ��ς̊Ԃ������č��Z��������������Ӗ������ɂ͂킩��܂���B
�����e�ɂȂ��Ă��܂��B�ł����A����������������邽�߂ɂ������Ă킩��ɂ������ɂȂ��Ă��܂��Ă��܂��B���l�̖��̓R�̎��^��H���e�[�}�Ƃ���'92�����嗝[3]�Ȃǂɂ�������̂ł����A�j���[�g���ȗ��A�����w�͔��ϕ��w�Ɩ��ڂȊW�ɂ���킯�ŁA�����ɁA�����Ɣ��ς̊Ԃ������č��Z��������������Ӗ������ɂ͂킩��܂���B
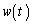 ���K�肷��������@���A�t���̔����@�̌�����p���āA
���K�肷��������@���A�t���̔����@�̌�����p���āA
t��w�̊��ƌ��āA���̗��ӂ�ϕ����A
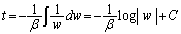 �@(C�F�ϕ��萔)�@����A
�@(C�F�ϕ��萔)�@����A
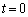 �̂Ƃ��A
�̂Ƃ��A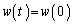 ���A
���A
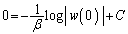 �@��
�@�� 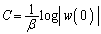
������A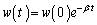
�Ƃ���A���̖��̗�������]���A���Z���ɂ킩��₷���Ǝ��͎v���܂�����ǂ��B
[3](��������)�@���́u�������_�v�ȂǕ��������Ƃ��Ȃ��̂ł킩��܂��A�f�M�ω�������Ђ���̕��́A�Ƃ����̂́A����(superstring)�̂��ƂȂ̂ł��傤���H���Ƃ�����A���̖��́A�����w�̍Ő�[�̘b����e�[�}�Ƃ��Ď��グ������I�Ȗ��ƌ����邩���m��܂���B
�u�����v�Ƃ����̂́A�A�C���V���^�C�����d�͂Ɠd���C�͂�I�ɋL�q���悤�Ƃ��Đ������Ȃ������u����ꗝ�_�v�̊�{�\���v�f�Ƃ��čl�����Ă�����̗̂L�͂Ȍ��ł����A�����_�ł��A���_�͖������Ō��ݐi�s�`�̏������ł��B�䂱���͂Ǝv�����́A����������ΊԈႢ�Ȃ��m�[�x���܂�����̂ŁA���Ѓ`�������W���Ē��������Ǝv���܂��B
�ł����A�����w�̍Ő�[�̘b��Ȃǎ��ɂƂ��Ă͂ǂ��ł��ǂ����ƂȂ̂ŁA���������Ӗ��s���̂��̂�������Ɏ����o�����Ǝ��ɂ͖��f�����m��܂���B��蕶�������u�ԂɁA��������H�Ɠ����o���Ă��܂�����������Ǝv���܂��B
�ł����A�����v���ɁA�ꌩ���č��Z�͈̔͂�E�p�����悤�ȃe�[�}�̖��́A�Ղ������Ƃ������̂ł��B���̖����������|���ŁA�Ђ���̕��̂̒������C�̂̑̐ςɓǂݑւ���A�J���m�[�E�T�C�N���̕��}�Ȗ��ɉ߂��܂���B�g�������̊�b�����́A�قڔM�͊w���@�������A��ԕ��������o�Ă��Ȃ��āA�f�M�ω��Ɠ����ω������o�Ă��܂���B�C�̕���̖��Ƃ��Ă��A���Ղȕ��ނɓ���Ǝv���܂��B���炭�A���̖��ɐ^���Ɏ��g���ǂ����ŁA���i�E�s���i�ɑ傫�����������낤�Ǝv���܂��B
�Ђ���̕��̂̒����ƋC�̂̑̐ς̈Ⴂ�́A�Ђ���̕��̂Ɏd��������ƒ��������傷��̂ɑ��A�C�̂Ɏd��������ƋC�̂̑̐ς͌�������A�Ƃ����_�ł��B�f�M�ω��ŁA�C�̂��̐ς傳����Ɖ��x��������(�f�M�c��)�A�C�̂��̐ς�����������Ɖ��x���オ��(�f�M���k)�܂��B���̕ӂ��A�J���m�[�E�T�C�N���̃O���t��I�ԂƂ���Œ��ӂ��Ȃ�������Ȃ��_�ł��B�ł����A�f�M�c����f�M���k�̕����A�l�Ԃ̎��R�Ȋ����Ƌt�ɂȂ��Ă���̂ŁA���̖��̏ݒ�͂ނ�����ɂ͍l���Ղ��̂ł͂Ȃ����Ƃ����C�����܂��B
�J���m�[�E�T�C�N���ł́A�T�C�N����������čŏ��̏�Ԃɖ߂��Ă���̂ŁA1�T�C�N���œ����G�l���M�[�̕ω��̓[���ɂȂ�܂��B������A�C�̂���Ή��x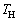 �̍��M������z�������M��
�̍��M������z�������M�� �C��Ή��x
�C��Ή��x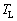 �̒�M���ɕ��o�����M��
�̒�M���ɕ��o�����M��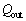 �Ƃ��āA�M����η �́A
�Ƃ��āA�M����η �́A
�ƂȂ邱�Ƃ́A�L�����Ă����Ă����͂Ȃ��Ǝv���܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B