京大物理'11年[2]
次の文を読んで、 に適した式を、それぞれの解答欄に記入せよ。なお、 はすでに で与えられたものと同じものを表す。また、問1では指示にしたがって、解答を解答欄に記入せよ。
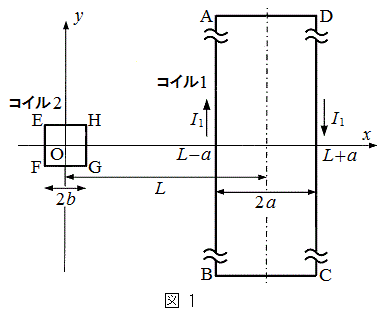 図1のように長方形の導線ABCDからなるコイル1と、正方形の導線EFGHからなるコイル2がxy平面内に置かれている。コイル2の中心は原点Oにあり、導線FGとEHはx軸に平行、導線EFとGHはy軸に平行な直線で、長さはいずれも
図1のように長方形の導線ABCDからなるコイル1と、正方形の導線EFGHからなるコイル2がxy平面内に置かれている。コイル2の中心は原点Oにあり、導線FGとEHはx軸に平行、導線EFとGHはy軸に平行な直線で、長さはいずれも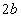 である。コイル2の電気抵抗はRである。コイル1の中心はx軸上の位置
である。コイル2の電気抵抗はRである。コイル1の中心はx軸上の位置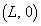 にあり、導線ABとCDの間隔は
にあり、導線ABとCDの間隔は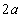 でそれぞれ
でそれぞれ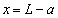 と
と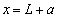 のy軸に平行な直線である。2つのコイルは重ならない(
のy軸に平行な直線である。2つのコイルは重ならない(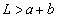 )とする。コイル1の導線ABとCDの長さは、コイル1の幅
)とする。コイル1の導線ABとCDの長さは、コイル1の幅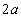 やコイル2の一辺
やコイル2の一辺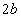 ,および、コイル1とコイル2の中心間の距離Lに比べて十分大きい。したがって、x軸の近くでは、導線ADとBCに流れる電流がつくる磁界(磁場)の強さは、導線ABやCDに流れる電流がつくる磁界に比べて十分小さく、無視できる。また、x軸の近くでは、導線ABやCDに流れる電流がつくる磁界は、無限に長い直線電流がつくる磁界とすることができる。これらのコイルは真空中に置かれており、真空の透磁率を
,および、コイル1とコイル2の中心間の距離Lに比べて十分大きい。したがって、x軸の近くでは、導線ADとBCに流れる電流がつくる磁界(磁場)の強さは、導線ABやCDに流れる電流がつくる磁界に比べて十分小さく、無視できる。また、x軸の近くでは、導線ABやCDに流れる電流がつくる磁界は、無限に長い直線電流がつくる磁界とすることができる。これらのコイルは真空中に置かれており、真空の透磁率を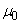 とする。
とする。
(1) まず、コイル1のADCBの向きに電流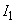 を流したときにできる磁界について考えよう。導線ABに流れる電流
を流したときにできる磁界について考えよう。導線ABに流れる電流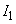 がx軸の近くの位置
がx軸の近くの位置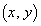 (ただし、
(ただし、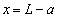 を除く)につくる磁界は、紙面に垂直に裏から表に向かう向きを正として、 イ である。x軸の近くの位置
を除く)につくる磁界は、紙面に垂直に裏から表に向かう向きを正として、 イ である。x軸の近くの位置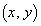 (ただし、
(ただし、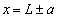 を除く)にコイル1がつくる磁界は、導線ABとCDの寄与を加えて ロ となる。
を除く)にコイル1がつくる磁界は、導線ABとCDの寄与を加えて ロ となる。
(2) コイル1に流れる電流がつくる磁界のもとで、中心が原点にあるコイル2を貫く磁束について考えよう。ただし、以下では、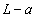 はコイル2の一辺
はコイル2の一辺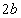 に比べて十分大きいとし、
に比べて十分大きいとし、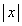 や
や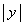 が
が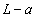 に比べて十分小さいような原点付近の位置
に比べて十分小さいような原点付近の位置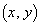 における磁界を考える。ここで、実数ε の絶対値が1に比べて十分小さいときに成立する近似式
における磁界を考える。ここで、実数ε の絶対値が1に比べて十分小さいときに成立する近似式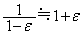 を用いると、コイル1のADCBの向きに電流
を用いると、コイル1のADCBの向きに電流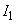 を流したとき、導線ABに流れる電流がつくる磁界 イ は、xy平面内の原点付近の位置
を流したとき、導線ABに流れる電流がつくる磁界 イ は、xy平面内の原点付近の位置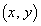 では、紙面に垂直に裏から表に向かう向きを正として、 ハ と近似できる。この近似を導線CDにも適用すると、コイル1に流れる電流がxy平面内の原点付近につくる磁界は ニ のようにxの1次関数で近似できる。以下でも、bや
では、紙面に垂直に裏から表に向かう向きを正として、 ハ と近似できる。この近似を導線CDにも適用すると、コイル1に流れる電流がxy平面内の原点付近につくる磁界は ニ のようにxの1次関数で近似できる。以下でも、bや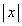 は
は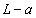 に比べて十分小さく、近似式 ニ が成立する範囲内で考える。このとき、コイル2を貫く磁束は、コイル2の中心での磁束密度に、コイル2の面積を乗じた値として計算できるので、 ホ となる。コイル1に流れる電流が時間変化するとき、コイル2に誘導起電力が発生する。このとき、コイル1とコイル2からなる回路の相互インダクタンスは ヘ となる。
に比べて十分小さく、近似式 ニ が成立する範囲内で考える。このとき、コイル2を貫く磁束は、コイル2の中心での磁束密度に、コイル2の面積を乗じた値として計算できるので、 ホ となる。コイル1に流れる電流が時間変化するとき、コイル2に誘導起電力が発生する。このとき、コイル1とコイル2からなる回路の相互インダクタンスは ヘ となる。
(3) 次に、コイル1のADCBの向きに流す電流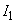 は一定とし、正方形コイル2をx軸に沿って正の向きに一定の速さvで移動させる場合を考えよう。時刻tにおけるコイル2の中心のx座標を
は一定とし、正方形コイル2をx軸に沿って正の向きに一定の速さvで移動させる場合を考えよう。時刻tにおけるコイル2の中心のx座標を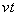 とする。コイル2の運動は原点付近に限り、2つのコイルは重ならず、また、(2)と同様に、bや
とする。コイル2の運動は原点付近に限り、2つのコイルは重ならず、また、(2)と同様に、bや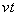 は
は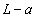 に比べて十分小さく、近似式 ニ が成立するものとする。時刻tにおいて、コイル2を貫く磁束は ト となる。コイル2の電気抵抗の値はRであるから、コイル2に生じる誘導起電力によりコイル2に流れる電流は、EFGHの向きを正として チ となる。ただし、コイル2の自己インダクタンスは無視できるとする。このとき、単位時間当たりにコイル2に発生するジュール熱は リ となる。
に比べて十分小さく、近似式 ニ が成立するものとする。時刻tにおいて、コイル2を貫く磁束は ト となる。コイル2の電気抵抗の値はRであるから、コイル2に生じる誘導起電力によりコイル2に流れる電流は、EFGHの向きを正として チ となる。ただし、コイル2の自己インダクタンスは無視できるとする。このとき、単位時間当たりにコイル2に発生するジュール熱は リ となる。
問1 時刻tにおいて、コイル1に流れる電流のつくる磁界からコイル2全体が受ける力の大きさと向きを、導出の過程も示して求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 相互インダクタンスを求めるのでやや目新しいですが、問題そのものは基本的です。
(1)(イ) 導線ABを流れる電流が位置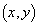 に作る磁界は、右ねじの法則より、
に作る磁界は、右ねじの法則より、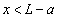 のとき紙面に垂直に裏から表に向かう向きで、位置
のとき紙面に垂直に裏から表に向かう向きで、位置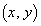 と導線ABとの距離が
と導線ABとの距離が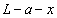 であることから、
であることから、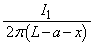 ......[答] (電流のつくる磁界を参照)
......[答] (電流のつくる磁界を参照) (ロ) 導線CDを流れる電流が位置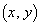 に作る磁界は、右ねじの法則より、
に作る磁界は、右ねじの法則より、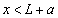 のとき紙面に垂直に表から裏に向かう向きで、位置
のとき紙面に垂直に表から裏に向かう向きで、位置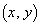 と導線CDとの距離が
と導線CDとの距離が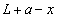 であることから、
であることから、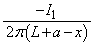 (
(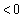 )
) 導線ABと導線CDの寄与を加えて、位置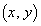 にコイル1がつくる磁界は、
にコイル1がつくる磁界は、 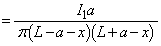 ......[答]
......[答]
(2)(ハ) 微小量εを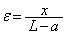 と見て問題文の近似式を使うと、導線ABを流れる電流が原点付近の位置
と見て問題文の近似式を使うと、導線ABを流れる電流が原点付近の位置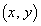 に作る磁界は、
に作る磁界は、 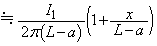 ......[答]
......[答](ニ) (ハ)と同様にして、導線CDに流れる電流が原点付近の位置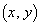 に作る磁界は、
に作る磁界は、 導線ABと導線CDの寄与を加えて、コイル1が原点付近の位置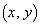 に作る磁界は、
に作る磁界は、 (ホ) コイル2の中心での磁界は、(ニ)の結果で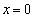 として
として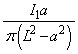 ,磁束密度は
,磁束密度は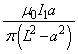 ,コイル2の面積は
,コイル2の面積は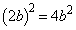 ,よって、コイル2を貫く磁束は、
,よって、コイル2を貫く磁束は、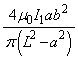 ......[答]
......[答] (ヘ) (ホ)の結果を用いると、時間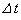 の間に電流
の間に電流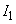 が
が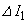 変化したときにコイル2に発生する起電力の大きさVは、電磁誘導の法則より、
変化したときにコイル2に発生する起電力の大きさVは、電磁誘導の法則より、 ∴ 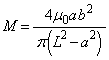 ......[答]
......[答]
(3)(ト) (ニ)の結果で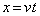 として、コイル1が原点付近の位置
として、コイル1が原点付近の位置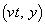 に作る磁界は、
に作る磁界は、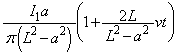
(ホ)と同様にして、コイル2を貫く磁束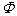 は、
は、 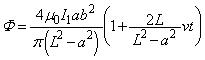 ......[答]
......[答](チ) コイル2を貫く磁界は、導線ABが導線CDよりもコイル2の近くにあるので、導線ABの影響を受けて導線ABがコイル2の中心に作る磁界の向き、つまり正の向きとなり、コイル2がx軸正方向に移動すると、コイル2を貫く磁束は増加するので、負の向きの磁界を作る向き(レンツの法則を参照)、つまり、EHGFの向きに誘導電流を流す向きに誘導起電力が発生します。EFGHの向きの電流を正としているので、誘導電流の向きは負です。 コイル2に発生する起電力の大きさVは、電磁誘導の法則より、
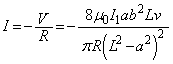 ......[答]
......[答](リ) 単位時間当たりにコイル2に発生するジュール熱は、 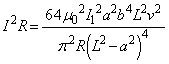 ......[答]
......[答]
問1 (リ)で求めた単位時間当たりのジュール熱は、コイル2をx軸に沿って正の向きに一定の速さvで移動させる外力Fの仕事率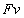 に等しくなります。
に等しくなります。 より、
コイル2は等速度運動するので、力のつり合いより、コイル1に流れる電流のつくる磁界からコイル2全体が受ける力は、この外力Fと等大逆向きで、大きさは、 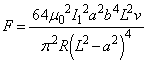 ......[答]
......[答]向きは、x軸負方向 ......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
京大物理TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
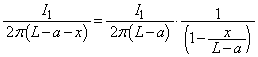
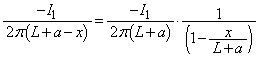
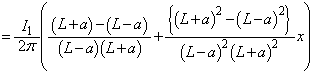
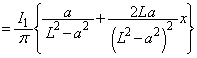
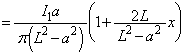 ......[答]
......[答]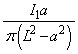 ,磁束密度は
,磁束密度は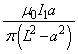 ,コイル2の面積は
,コイル2の面積は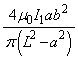 ......[答]
......[答]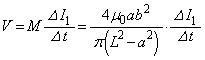
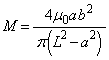 ......[答]
......[答]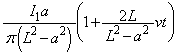
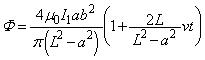 ......[答]
......[答]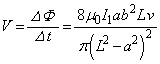
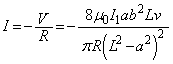 ......[答]
......[答]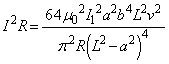 ......[答]
......[答]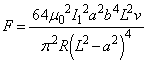 ......[答]
......[答]