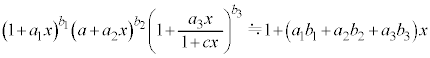京都大学2020年前期物理入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] 次の文章を読んで、 に適した式または数値を、それぞれの解答欄に記入せよ。なお、 はすでに で与えられたものと同じものを表す。また、問1では、指示にしたがって、解答を解答欄に記入せよ。
以下では、ばね定数kで自然長 のばね、および長さLの糸を用いる。ばねや糸の質量は無視できるものとし、重力加速度の大きさを
のばね、および長さLの糸を用いる。ばねや糸の質量は無視できるものとし、重力加速度の大きさを ,円周率をπとする。
,円周率をπとする。
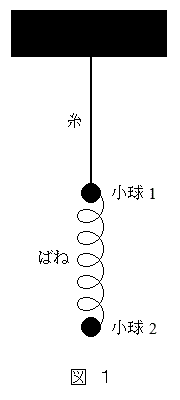 (1) 図1のように、質量mの2つの小球(質点)を糸とばねでつるし、つり合いの位置で静止させた。2つの小球は鉛直方向にのみ運動するものとし、糸がたるんでいないときの小球1の位置を原点として、鉛直下向きを座標軸の正の向きとする。また、小球1は天井にぶつからず、小球同士は衝突しないものとする。
(1) 図1のように、質量mの2つの小球(質点)を糸とばねでつるし、つり合いの位置で静止させた。2つの小球は鉛直方向にのみ運動するものとし、糸がたるんでいないときの小球1の位置を原点として、鉛直下向きを座標軸の正の向きとする。また、小球1は天井にぶつからず、小球同士は衝突しないものとする。いま、小球2をつり合いの位置から長さdだけ引き下げ、静かに手を離す。dが十分に小さいときは、運動の途中で糸はたるまず、小球2は位置 ア を中心とした、振幅 イ の単振動をおこなう。dがある値より大きいときは、運動の途中で糸がたるむ。小球1にはたらく重力、糸の張力、ばねの力のつり合いを考えると、糸がたるみ始めた瞬間の小球2の位置はm,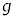 ,k,
,k,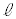 を用いて ウ と表されるので、運動の途中で糸がたるむための条件は、d > エ とわかる。
を用いて ウ と表されるので、運動の途中で糸がたるむための条件は、d > エ とわかる。
次に、dが十分に大きく、糸がたるむ場合の運動を考えよう。小球1,2の位置をそれぞれ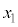 ,
,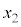 とし、重心の位置
とし、重心の位置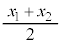 ,および小球1からみた小球2の相対位置
,および小球1からみた小球2の相対位置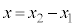 について、糸がたるみ始めてから再びたるみがなくなるまでの運動を考える。2つの小球にはたらくばねの力は、互いに逆向きで大きさが等しいので、重心はばねの力の影響を受けずに鉛直投げ上げ運動をおこなう。糸がたるみ始めた瞬間における重心の速さをm,
について、糸がたるみ始めてから再びたるみがなくなるまでの運動を考える。2つの小球にはたらくばねの力は、互いに逆向きで大きさが等しいので、重心はばねの力の影響を受けずに鉛直投げ上げ運動をおこなう。糸がたるみ始めた瞬間における重心の速さをm,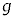 ,k,dを用いて表すと オ となる。一方、2つの小球にはたらく重力は、向きが同じで大きさが等しいので、相対位置xは重力の影響を受けずにばねの力で単振動をおこない、その周期は カ で与えられる。また、小球1の速度が最小値をとる瞬間において、小球1からみた小球2の相対速度は キ × オ とわかる。
,k,dを用いて表すと オ となる。一方、2つの小球にはたらく重力は、向きが同じで大きさが等しいので、相対位置xは重力の影響を受けずにばねの力で単振動をおこない、その周期は カ で与えられる。また、小球1の速度が最小値をとる瞬間において、小球1からみた小球2の相対速度は キ × オ とわかる。
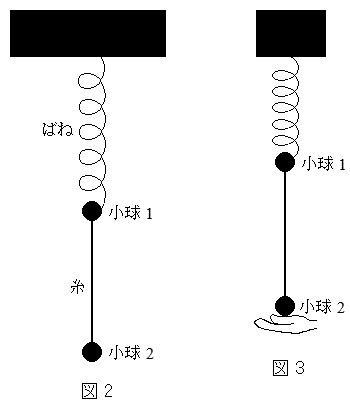 (2) 図2のように、質量mの2つの小球(質点)をばねと糸でつるす。2つの小球は鉛直方向にのみ運動するものとし、ばねが自然長のときの小球1の位置を原点として、鉛直下向きを座標軸の正の向きとする。いま図3のように、小球2を支えて静止させたところ、糸はたるまず張力が0であり、小球1も静止していたとする。このとき、小球1の位置は ク である。この状態から、時刻0に小球2を上方に速さvで打ち上げた。
(2) 図2のように、質量mの2つの小球(質点)をばねと糸でつるす。2つの小球は鉛直方向にのみ運動するものとし、ばねが自然長のときの小球1の位置を原点として、鉛直下向きを座標軸の正の向きとする。いま図3のように、小球2を支えて静止させたところ、糸はたるまず張力が0であり、小球1も静止していたとする。このとき、小球1の位置は ク である。この状態から、時刻0に小球2を上方に速さvで打ち上げた。まず、打ち上げ後に、小球2が小球1に衝突せず落下に転じる場合を考える。小球2が落下し、打ち上げられた位置に戻ってきたとき、糸のたるみがなくなる。たるみがなくなる前後で小球1,2の力学的エネルギーの和は保存されるものとすると、たるみがなくなった直後には、小球2の速度は ケ であり、小球1は振幅が コ の単振動を始める。
次に、打ち上げ後に、小球2が落下せず小球1と弾性衝突する場合を考える。衝突直後の小球1の速さ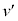 は、v,
は、v,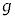 ,Lを用いて サ と表される。衝突後、2つの小球は糸がたるんだまま運動し、小球1が衝突時の位置に戻るまでのある時刻Tに糸のたるみがなくなった。その直後からしばらくの間、糸のたるみがないまま運動が続く条件を考えよう。まず、時刻Tに、小球の間の距離はLである。また、たるみがなくなる前後で小球1,2の力学的エネルギーの和は保存されるものとすると、時刻Tの直後に糸がたるまないためには、時刻Tの直前に小球1からみた小球2の速度は シ でなければならない。よって、小球1にはたらくばねの力Fは、時刻Tの直前に
,Lを用いて サ と表される。衝突後、2つの小球は糸がたるんだまま運動し、小球1が衝突時の位置に戻るまでのある時刻Tに糸のたるみがなくなった。その直後からしばらくの間、糸のたるみがないまま運動が続く条件を考えよう。まず、時刻Tに、小球の間の距離はLである。また、たるみがなくなる前後で小球1,2の力学的エネルギーの和は保存されるものとすると、時刻Tの直後に糸がたるまないためには、時刻Tの直前に小球1からみた小球2の速度は シ でなければならない。よって、小球1にはたらくばねの力Fは、時刻Tの直前に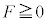 である(鉛直下向きを正とする)。一方、時刻Tには糸のたるみがないため張力が0以上であるが、そのとき
である(鉛直下向きを正とする)。一方、時刻Tには糸のたるみがないため張力が0以上であるが、そのとき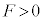 ならば直後に糸がたるんでしまう。以上のことより、いま考えている運動においては、時刻Tに小球1の位置は ス でなければならない。2つの小球の力学的エネルギーが、衝突後から時刻Tの間はそれぞれ保存することを考えると、得られた条件より打ち上げの速さvは、m,
ならば直後に糸がたるんでしまう。以上のことより、いま考えている運動においては、時刻Tに小球1の位置は ス でなければならない。2つの小球の力学的エネルギーが、衝突後から時刻Tの間はそれぞれ保存することを考えると、得られた条件より打ち上げの速さvは、m,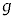 ,k,Lを用いて表される関係式
,k,Lを用いて表される関係式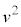 = セ を満たすことがわかる。
= セ を満たすことがわかる。
 問1 小球同士が弾性衝突した時刻を
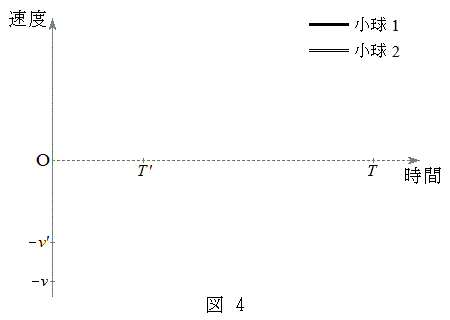
問1 小球同士が弾性衝突した時刻を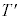 とする。図4を解答欄に描き写し、時刻0からTまでの、小球の速度を表すグラフを描け。なお、小球1を実線で、小球2を二重線で表すこととする。図4に示されている値以外に、速度や時間の値を書き加える必要はない。
とする。図4を解答欄に描き写し、時刻0からTまでの、小球の速度を表すグラフを描け。なお、小球1を実線で、小球2を二重線で表すこととする。図4に示されている値以外に、速度や時間の値を書き加える必要はない。
[解答へ]
[2] 次の文章を読んで、 に適した式または数値を、それぞれの解答欄に記入せよ。なお、
に適した式または数値を、それぞれの解答欄に記入せよ。なお、 はすでに
はすでに で与えられたものと同じものを表す。また、問1〜問3では、指示にしたがって、解答をそれぞれの解答欄に記入せよ。ただし、円周率をπとする。
で与えられたものと同じものを表す。また、問1〜問3では、指示にしたがって、解答をそれぞれの解答欄に記入せよ。ただし、円周率をπとする。 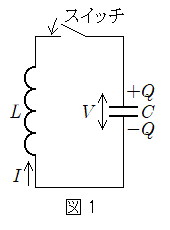
(1) 図1のように、自己インダクタンスLのコイル、スイッチ、電気容量Cのコンデンサーからなる回路がある。コンデンサーに蓄えられる電気量Qとコンデンサーの両端に現れる電圧Vの間には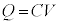 の関係が成り立つ。コンデンサーに初期の電気量
の関係が成り立つ。コンデンサーに初期の電気量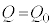 (
(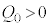 )を与え、スイッチを閉じたところ、周期
)を与え、スイッチを閉じたところ、周期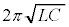 の電気振動が発生した。このとき、図1のコイルを流れる矢印の方向を正とした電流Iについて、微小時間
の電気振動が発生した。このとき、図1のコイルを流れる矢印の方向を正とした電流Iについて、微小時間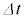 の間の微小変化を
の間の微小変化を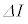 とすると、コイルの誘導起電力とコンデンサーの電圧Vの間には
とすると、コイルの誘導起電力とコンデンサーの電圧Vの間には 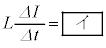 (i)
(i)の関係がある。スイッチを閉じた後、電流Iは初期値0から負方向に流れ始める。
また、コンデンサーに蓄えられた電気量Qと電圧Vの微小変化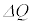 ,
,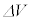 の間に、
の間に、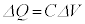 の関係がある。電気量Qは電流Iが負の場合は減少し、
の関係がある。電気量Qは電流Iが負の場合は減少し、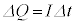 が成り立つので、微小時間
が成り立つので、微小時間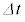 の間の電圧Vの微小変化
の間の電圧Vの微小変化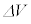 と電流Iの間には
と電流Iの間には 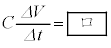 (ii)
(ii)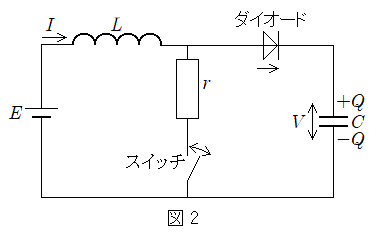
(2) 図2のように、電圧Eの直流電源、自己インダクタンスLのコイル、スイッチ、抵抗値rの抵抗、ダイオード、電気容量Cのコンデンサーからなる回路がある。ダイオードは理想的な整流作用をもつとし、矢印で示した順方向の抵抗は0、逆方向の抵抗は無限大とする。
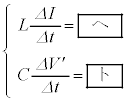 (iii)
(iii)の関係がある。式(iii)は式(i),(ii)と同じ形をしているため、初期値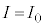 ,
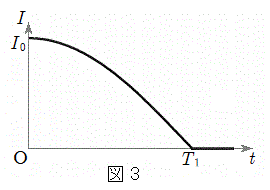
,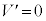 の電気振動が始まるが、ダイオードが存在するためにIは負にならず、図3のように時刻
の電気振動が始まるが、ダイオードが存在するためにIは負にならず、図3のように時刻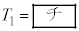 に振動は停止する。
に振動は停止する。
問1 コイルに蓄えられていた初期のエネルギー、電源から供給されるエネルギー、コンデンサーに蓄積されるエネルギーの関係から時刻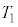 におけるコンデンサーの両端に現れる電圧を求め、Vの時間変化を図3と同様に描け。
におけるコンデンサーの両端に現れる電圧を求め、Vの時間変化を図3と同様に描け。 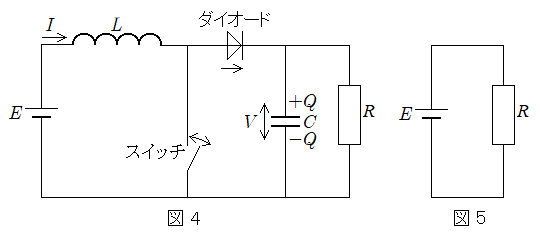
(3) 図2の回路から抵抗値rの抵抗を取り去り、抵抗値Rの抵抗を加えた図4の回路を、電源と抵抗を直接接続した図5の回路と比較してみよう。ただし、図4の回路ではスイッチを微小時間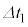 だけ閉じ、その後微小時間
だけ閉じ、その後微小時間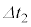 だけ開ける操作を微小時間
だけ開ける操作を微小時間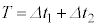 で周期的にくりかえすものとする。また、微小時間
で周期的にくりかえすものとする。また、微小時間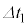 の間のコイルを流れる電流I,コンデンサーの両端に現れる電圧Vの微小変化をそれぞれ
の間のコイルを流れる電流I,コンデンサーの両端に現れる電圧Vの微小変化をそれぞれ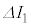 ,
,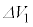 ,微小時間
,微小時間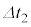 の間のI,Vの微小変化をそれぞれ
の間のI,Vの微小変化をそれぞれ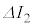 ,
,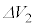 とする。
とする。 スイッチが閉じた状態では、電圧Vを正とするとダイオードに電流は流れず、電源の電圧Eにより電流Iは増加、コンデンサーは抵抗Rを通して放電し
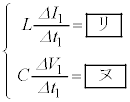 (iv)
(iv)の関係が成立する。スイッチが開いた状態では、電流Iを正とするとダイオードに電流が流れ
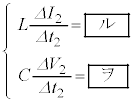 (v)
(v)の関係が成立する。
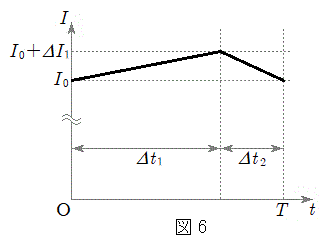 十分時間がたち、I,Vが微小時間Tで周期的に変化する定常状態になったときの1周期
十分時間がたち、I,Vが微小時間Tで周期的に変化する定常状態になったときの1周期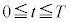 の間の電流Iの変化は図6のようになった。ただし、スイッチを閉じた瞬間を
の間の電流Iの変化は図6のようになった。ただし、スイッチを閉じた瞬間を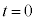 とし、そのときの電流Iと電圧Vをそれぞれ、
とし、そのときの電流Iと電圧Vをそれぞれ、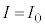 ,
,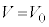 とおく。また、定常状態の
とおく。また、定常状態の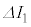 ,
,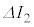 ,
,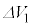 ,
,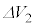 は、式(iv),(v)において
は、式(iv),(v)において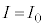 ,
,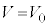 を代入することにより、
を代入することにより、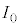 ,
,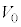 を用いて表現できるものとする。
を用いて表現できるものとする。
問2 定常状態になったときの1周期では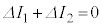 ,
,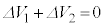 が成り立つ。
が成り立つ。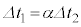 のとき、電圧
のとき、電圧 ,電流
,電流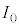 をα,E,Rのうち必要なものを用いて表せ。また、
をα,E,Rのうち必要なものを用いて表せ。また、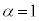 の場合の電圧Vの変化を、図6を参考にE,C,R,Tのうち必要なものを用いて描け。
の場合の電圧Vの変化を、図6を参考にE,C,R,Tのうち必要なものを用いて描け。
問3 問2で得られたように、図4の回路は電源の電圧Eよりも大きな電圧Vを作り出すことができる。ここで図4と図5の抵抗で消費される電力を考える。コンデンサーの両端に現れる電圧Vは、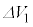 ,
,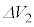 が
が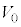 より十分小さいとき、
より十分小さいとき、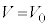 の一定値とみなせる。この場合、
の一定値とみなせる。この場合、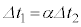 のとき、図4の抵抗で消費される電力は図5の抵抗で消費される電力の何倍になるか、αを用いて答えよ。
のとき、図4の抵抗で消費される電力は図5の抵抗で消費される電力の何倍になるか、αを用いて答えよ。
[解答へ]
[3] 次の文章を読んで、 に適した式または数値を、それぞれの解答欄に記入せよ。なお、
に適した式または数値を、それぞれの解答欄に記入せよ。なお、 はすでに
はすでに で与えられたものと同じものを表す。また、問1,問2では、指示にしたがって、解答をそれぞれの解答欄に記入せよ。
で与えられたものと同じものを表す。また、問1,問2では、指示にしたがって、解答をそれぞれの解答欄に記入せよ。
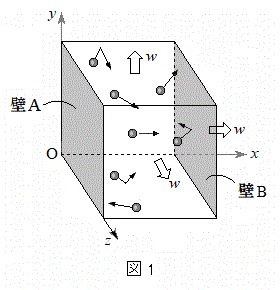
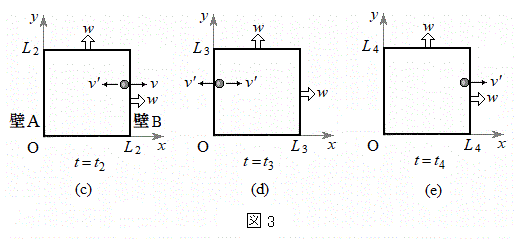
図1のように、x軸、y軸、z軸を3辺とする立方体の箱の中を多数の粒子(質量m)が、壁面に衝突しながら運動している。この立方体の各辺の長さは一定の速さwで時間とともに増大する。すなわち、時刻t における各辺の長さは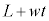 であるとする(Lは定数)。したがって、立方体の各面の面積も時間とともに大きくなる。具体的には、原点Oを頂点とする3つの面はそれぞれの位置に固定され、他の3つの面がそれぞれに垂直な方向に一定の速さwで移動するとする。ただし、各面が移動する速さwは粒子の速さに比べて十分に小さいとする。以下では、
であるとする(Lは定数)。したがって、立方体の各面の面積も時間とともに大きくなる。具体的には、原点Oを頂点とする3つの面はそれぞれの位置に固定され、他の3つの面がそれぞれに垂直な方向に一定の速さwで移動するとする。ただし、各面が移動する速さwは粒子の速さに比べて十分に小さいとする。以下では、 の位置にある面を壁A,それに対面し、x軸の正の向きに速さwで移動する面を壁Bと呼ぶ。粒子にはたらく重力の影響は無視する。
の位置にある面を壁A,それに対面し、x軸の正の向きに速さwで移動する面を壁Bと呼ぶ。粒子にはたらく重力の影響は無視する。
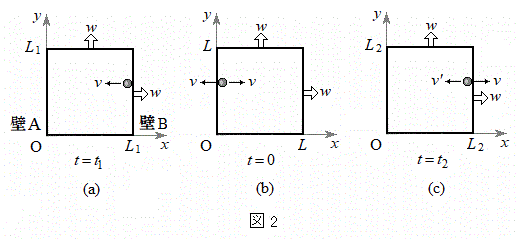 以下では簡単のために、速度がx軸の正あるいは負の方向を向いた1つの粒子を考え、まず、図2の(a)→(b)→(c)で表された過程を考察する。この粒子と他の粒子との衝突はないものとする。図2は、図1の立方体をz軸の正の側から見たものである。時刻
以下では簡単のために、速度がx軸の正あるいは負の方向を向いた1つの粒子を考え、まず、図2の(a)→(b)→(c)で表された過程を考察する。この粒子と他の粒子との衝突はないものとする。図2は、図1の立方体をz軸の正の側から見たものである。時刻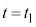 (
(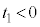 )において、立方体の辺の長さは
)において、立方体の辺の長さは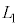 であり、粒子は壁B上にあって速度はx軸の負の方向を向き、その大きさはvであるとする。その後、時刻
であり、粒子は壁B上にあって速度はx軸の負の方向を向き、その大きさはvであるとする。その後、時刻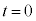 において粒子は壁Aに弾性衝突し、衝突後の速度はx軸の正の向きに大きさvとなった。
において粒子は壁Aに弾性衝突し、衝突後の速度はx軸の正の向きに大きさvとなった。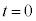 における立方体の辺の長さはLである。さらに時刻
における立方体の辺の長さはLである。さらに時刻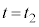 (
(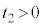 )において、粒子は壁Bに弾性衝突し、直後の速度はx軸の負の向きに大きさ
)において、粒子は壁Bに弾性衝突し、直後の速度はx軸の負の向きに大きさ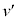 となった。
となった。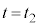 における立方体の辺の長さは
における立方体の辺の長さは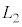 であった。
であった。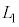 と
と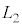 をL,v,wを用いて表すと
をL,v,wを用いて表すと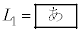 ,
,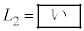 であり、図2の過程の時間
であり、図2の過程の時間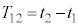 はL,v,wを用いて
はL,v,wを用いて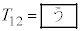 と表される。さらに、wはvに比べて十分に小さいため、
と表される。さらに、wはvに比べて十分に小さいため、 をL,v,
をL,v,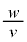 で表し、微小な
で表し、微小な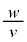 の2次以上を無視する近似を行うと、
の2次以上を無視する近似を行うと、 となる。なお、必要ならその絶対値が微小な実数xに対する近似式
となる。なお、必要ならその絶対値が微小な実数xに対する近似式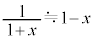 を用いてよい。壁Aが粒子から受けるx軸方向の力の時間平均
を用いてよい。壁Aが粒子から受けるx軸方向の力の時間平均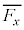 は、粒子が受ける力積
は、粒子が受ける力積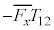 が時刻
が時刻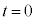 における衝突での粒子のx軸方向の運動量変化に等しいとした関係式から求まる。そこで、壁Aが粒子から受ける圧力Pを、
における衝突での粒子のx軸方向の運動量変化に等しいとした関係式から求まる。そこで、壁Aが粒子から受ける圧力Pを、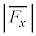 を壁Aの面積で割ったものとする。
を壁Aの面積で割ったものとする。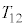 として
として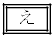 を用い、壁Aの面積を衝突時刻
を用い、壁Aの面積を衝突時刻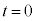 での
での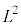 であるとすると、m,v,Lを用いて
であるとすると、m,v,Lを用いて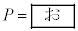 となる。なお、
となる。なお、 はwにはよらない量である。
はwにはよらない量である。
 次に、図3の(c)→(d)→(e)で表される、時刻
次に、図3の(c)→(d)→(e)で表される、時刻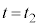 に速さ
に速さ で壁Bを離れた粒子が、再び壁Aに弾性衝突し、壁Bに戻ってくるまでの過程を考える。まず、
で壁Bを離れた粒子が、再び壁Aに弾性衝突し、壁Bに戻ってくるまでの過程を考える。まず、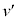 はvとwにより
はvとwにより
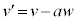 (i)
(i)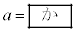 である。しかし、以下の解答では、指定された場合を除き、
である。しかし、以下の解答では、指定された場合を除き、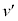 をvとwで表す際は、aを用いた式(i)の右辺の表式を用いること。粒子が時刻
をvとwで表す際は、aを用いた式(i)の右辺の表式を用いること。粒子が時刻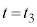 に壁Aに弾性衝突した時の立方体の辺の長さ
に壁Aに弾性衝突した時の立方体の辺の長さ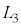 はL,v,
はL,v,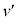 ,wを用いて
,wを用いて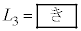 となる。図3の過程により壁Aが粒子から受ける圧力
となる。図3の過程により壁Aが粒子から受ける圧力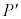 は、図2の過程に対する
は、図2の過程に対する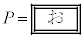 の結果において、vを
の結果において、vを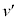 に、Lを
に、Lを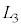 に置き換えることで得られる。そこで、圧力の変化分
に置き換えることで得られる。そこで、圧力の変化分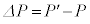 を考え、比
を考え、比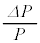 を
を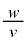 の関数として表し、
の関数として表し、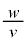 の2次以上を無視すると
の2次以上を無視すると
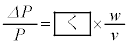 (ii)
(ii) はaを用いて表される量である。式(ii)の導出において、必要なら、その絶対値が微小な実数xの2次以上を無視する近似で
はaを用いて表される量である。式(ii)の導出において、必要なら、その絶対値が微小な実数xの2次以上を無視する近似で
であることを用いてよい。ここで、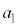 ,
,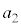 ,
,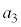 ,
,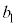 ,
,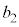 ,
,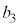 ,cは任意の実数である。
,cは任意の実数である。
さらに、図2の過程での粒子の壁Aへの衝突時刻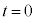 における立方体の体積
における立方体の体積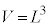 と、図3の過程での衝突時刻
と、図3の過程での衝突時刻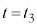 における体積
における体積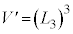 に対して、体積の変化分
に対して、体積の変化分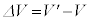 を考える。比
を考える。比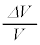 を
を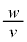 の関数として表し、
の関数として表し、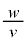 の2次以上を無視すると
の2次以上を無視すると
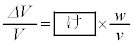 (iii)
(iii)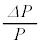 と
と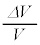 の間に
の間に
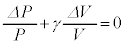 (iv)
(iv)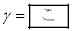 で与えられる。
で与えられる。
以上の式(iv)の導出は、x軸方向にのみ運動する1つの粒子に注目したものであり、圧力Pはその粒子のみから壁Aが受ける圧力であった。しかし、Pをあらゆる方向に運動する全ての粒子から壁Aが受ける圧力とし、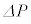 と
と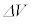 を与えられた微小時間内での変化分としても、式(iv)が成り立つことが示される。さらに、Pが
を与えられた微小時間内での変化分としても、式(iv)が成り立つことが示される。さらに、Pが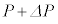 に、Vが
に、Vが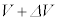 に微小に変化する間に立方体内の粒子からなる理想気体の絶対温度がTから
に微小に変化する間に立方体内の粒子からなる理想気体の絶対温度がTから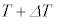 に微小に変化したとすると、式(iv)は理想気体の状態方程式を用いることで、
に微小に変化したとすると、式(iv)は理想気体の状態方程式を用いることで、
と表すこともできる。ここで、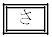 はγを用いて表される量であり、微小量
はγを用いて表される量であり、微小量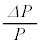 ,
, ,
,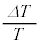 の2次以上を無視した。
の2次以上を無視した。
関係式(iv)は、理想気体の断熱変化におけるポアソンの法則として知られたものであり、aの値 を代入したγの値
を代入したγの値 は単原子分子気体のものを再現している。しかし、多原子分子気体の場合は、式(iv)の定数γは
は単原子分子気体のものを再現している。しかし、多原子分子気体の場合は、式(iv)の定数γは とは異なる値をとる。
とは異なる値をとる。
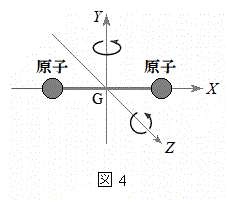 そこで、図1の立方体内をx軸方向に運動する1粒子を再び考え、次のようなモデルを用いて、二原子分子気体に対する式(iv)のγを求めてみよう。二原子分子を2つの質点(原子)が長さ一定で質量を無視できるまっすぐな棒でつながったものと見なすと、この二原子分子には重心の並進運動の他に、図4のように、重心(図4の原点G)のまわりの、Y軸とZ軸を回転軸とする2つの回転運動がある。いま、図1の立方体の中をx軸方向に並進運動する二原子分子に対して図2と図3の過程を考える。この二原子分子のエネルギーEは、重心のx軸方向の並進運動のエネルギー
そこで、図1の立方体内をx軸方向に運動する1粒子を再び考え、次のようなモデルを用いて、二原子分子気体に対する式(iv)のγを求めてみよう。二原子分子を2つの質点(原子)が長さ一定で質量を無視できるまっすぐな棒でつながったものと見なすと、この二原子分子には重心の並進運動の他に、図4のように、重心(図4の原点G)のまわりの、Y軸とZ軸を回転軸とする2つの回転運動がある。いま、図1の立方体の中をx軸方向に並進運動する二原子分子に対して図2と図3の過程を考える。この二原子分子のエネルギーEは、重心のx軸方向の並進運動のエネルギー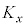 と重心のまわりの2つの回転運動のエネルギーの和であるとし、各回転運動のエネルギーの値がどれも
と重心のまわりの2つの回転運動のエネルギーの和であるとし、各回転運動のエネルギーの値がどれも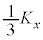 に等しく、
に等しく、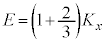 の関係が常に成り立っていると仮定する。この場合の、図2(c)で表された、時刻
の関係が常に成り立っていると仮定する。この場合の、図2(c)で表された、時刻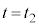 における分子と壁Bの衝突後の分子の速さ
における分子と壁Bの衝突後の分子の速さ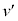 を求めるために、この衝突を二原子分子(質量m)と壁Bに対応した重い物体(質量M)のx軸方向の衝突過程に置き換え、最後に質量Mを質量mに比べて十分に大きくする。この衝突において、図4の二原子分子の構造を直接に考慮する必要はなく、二原子分子は上記のエネルギーEを持った質量mの粒子と考えればよい。衝突前後の分子と物体の速度は図5の通りとする。
を求めるために、この衝突を二原子分子(質量m)と壁Bに対応した重い物体(質量M)のx軸方向の衝突過程に置き換え、最後に質量Mを質量mに比べて十分に大きくする。この衝突において、図4の二原子分子の構造を直接に考慮する必要はなく、二原子分子は上記のエネルギーEを持った質量mの粒子と考えればよい。衝突前後の分子と物体の速度は図5の通りとする。
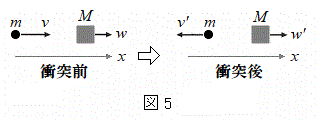
問1 図5の衝突過程におけるエネルギー保存と運動量保存の関係式を書きくだせ。それらより、衝突後の二原子分子の速さ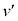 をv,w,
をv,w,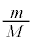 を用いて表わせ。なお、
を用いて表わせ。なお、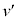 を導出する途中計算を書く必要はない。
を導出する途中計算を書く必要はない。
問2 問1で求めた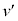 においてMをmに比べて十分に大きくする。すなわち、
においてMをmに比べて十分に大きくする。すなわち、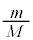 を近似的に0として、二原子分子気体の場合の式(i)のaの値と式(iv)のγの値を求めよ。
を近似的に0として、二原子分子気体の場合の式(i)のaの値と式(iv)のγの値を求めよ。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
京大物理TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 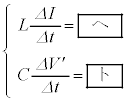 (iii)
(iii) (iv)
(iv)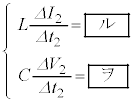 (v)
(v)