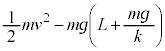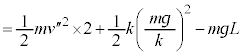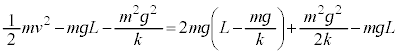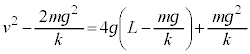���啨��'20�N�O��[1]
���̕��͂�ǂ�ŁA�@�@�ɓK�������܂��͐��l���A���ꂼ��̉��ɋL������B�Ȃ��A�@�@�͂��ł��@�@�ŗ^����ꂽ���̂Ɠ������̂�\���B�܂��A��1�ł́A�w���ɂ��������āA�����ɋL������B
�ȉ��ł́A�˒萔k�Ŏ��R��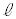 �̂ˁA����ђ���L�̎���p����B�˂⎅�̎��ʂ͖����ł�����̂Ƃ��A�d�͉����x�̑傫����
�̂ˁA����ђ���L�̎���p����B�˂⎅�̎��ʂ͖����ł�����̂Ƃ��A�d�͉����x�̑傫����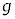 �C�~������π�Ƃ���B
�C�~������π�Ƃ���B
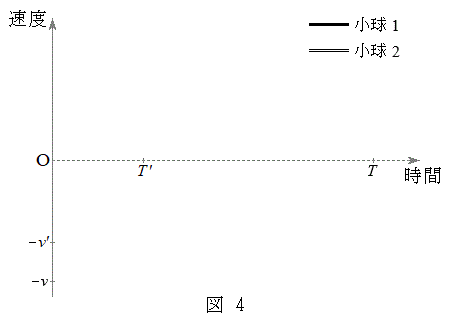
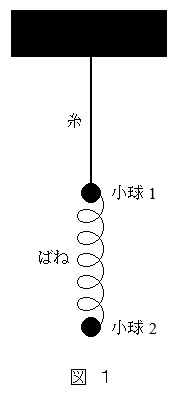 (1) �}1�̂悤�ɁA����m��2�̏���(���_)�����Ƃ˂ł邵�A�荇���̈ʒu�ŐÎ~�������B2�̏����͉��������ɂ̂݉^��������̂Ƃ��A���������ł��Ȃ��Ƃ��̏���1�̈ʒu�����_�Ƃ��āA���������������W���̐��̌����Ƃ���B�܂��A����1�͓V��ɂԂ��炸�A�������m�͏Փ˂��Ȃ����̂Ƃ���B
(1) �}1�̂悤�ɁA����m��2�̏���(���_)�����Ƃ˂ł邵�A�荇���̈ʒu�ŐÎ~�������B2�̏����͉��������ɂ̂݉^��������̂Ƃ��A���������ł��Ȃ��Ƃ��̏���1�̈ʒu�����_�Ƃ��āA���������������W���̐��̌����Ƃ���B�܂��A����1�͓V��ɂԂ��炸�A�������m�͏Փ˂��Ȃ����̂Ƃ���B���܁A����2���荇���̈ʒu���璷��d�������������A�Â��Ɏ�𗣂��Bd���\���ɏ������Ƃ��́A�^���̓r���Ŏ��͂���܂��A����2�͈ʒu�@�A�@�𒆐S�Ƃ����A�U���@�C�@�̒P�U���������Ȃ��Bd������l���傫���Ƃ��́A�^���̓r���Ŏ�������ށB����1�ɂ͂��炭�d�́A���̒��́A�˂̗͂̂荇�����l����ƁA��������ݎn�߂��u�Ԃ̏���2�̈ʒu��m�C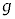 �Ck�C
�Ck�C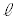 ��p�����@�E�@�ƕ\�����̂ŁA�^���̓r���Ŏ�������ނ��߂̏����́Ad > �@�G�@�Ƃ킩��B
��p�����@�E�@�ƕ\�����̂ŁA�^���̓r���Ŏ�������ނ��߂̏����́Ad > �@�G�@�Ƃ킩��B
���ɁAd���\���ɑ傫���A��������ޏꍇ�̉^�����l���悤�B����1�C2�̈ʒu�����ꂼ��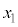 �C
�C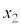 �Ƃ��A�d�S�̈ʒu
�Ƃ��A�d�S�̈ʒu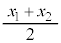 �C����я���1����݂�����2�̑��Έʒu
�C����я���1����݂�����2�̑��Έʒu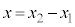 �ɂ��āA��������ݎn�߂Ă���Ăт���݂��Ȃ��Ȃ�܂ł̉^�����l����B2�̏����ɂ͂��炭�˂̗͂́A�݂��ɋt�����ő傫�����������̂ŁA�d�S�͂˂̗͂̉e�������ɉ��������グ�^���������Ȃ��B��������ݎn�߂��u�Ԃɂ�����d�S�̑�����m�C
�ɂ��āA��������ݎn�߂Ă���Ăт���݂��Ȃ��Ȃ�܂ł̉^�����l����B2�̏����ɂ͂��炭�˂̗͂́A�݂��ɋt�����ő傫�����������̂ŁA�d�S�͂˂̗͂̉e�������ɉ��������グ�^���������Ȃ��B��������ݎn�߂��u�Ԃɂ�����d�S�̑�����m�C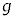 �Ck�Cd��p���ĕ\�����@�I�@�ƂȂ�B����A2�̏����ɂ͂��炭�d�͂́A�����������ő傫�����������̂ŁA���Έʒux�͏d�͂̉e�������ɂ˂̗͂ŒP�U���������Ȃ��A���̎������@�J�@�ŗ^������B�܂��A����1�̑��x���ŏ��l���Ƃ�u�Ԃɂ����āA����1����݂�����2�̑��Α��x���@�L�@�~�@�I�@�Ƃ킩��B
�Ck�Cd��p���ĕ\�����@�I�@�ƂȂ�B����A2�̏����ɂ͂��炭�d�͂́A�����������ő傫�����������̂ŁA���Έʒux�͏d�͂̉e�������ɂ˂̗͂ŒP�U���������Ȃ��A���̎������@�J�@�ŗ^������B�܂��A����1�̑��x���ŏ��l���Ƃ�u�Ԃɂ����āA����1����݂�����2�̑��Α��x���@�L�@�~�@�I�@�Ƃ킩��B
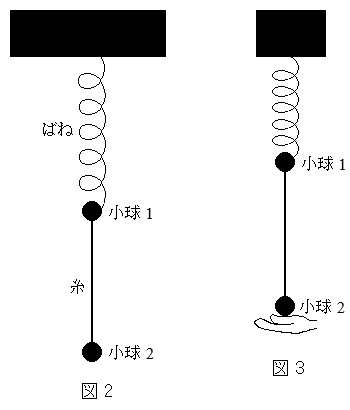 (2) �}2�̂悤�ɁA����m��2�̏���(���_)���˂Ǝ��ł邷�B2�̏����͉��������ɂ̂݉^��������̂Ƃ��A�˂����R���̂Ƃ��̏���1�̈ʒu�����_�Ƃ��āA���������������W���̐��̌����Ƃ���B���ܐ}3�̂悤�ɁA����2���x���ĐÎ~�������Ƃ���A���͂���܂����͂�0�ł���A����1���Î~���Ă����Ƃ���B���̂Ƃ��A����1�̈ʒu���@�N�@�ł���B���̏�Ԃ���A����0�ɏ���2������ɑ���v�őł��グ���B
(2) �}2�̂悤�ɁA����m��2�̏���(���_)���˂Ǝ��ł邷�B2�̏����͉��������ɂ̂݉^��������̂Ƃ��A�˂����R���̂Ƃ��̏���1�̈ʒu�����_�Ƃ��āA���������������W���̐��̌����Ƃ���B���ܐ}3�̂悤�ɁA����2���x���ĐÎ~�������Ƃ���A���͂���܂����͂�0�ł���A����1���Î~���Ă����Ƃ���B���̂Ƃ��A����1�̈ʒu���@�N�@�ł���B���̏�Ԃ���A����0�ɏ���2������ɑ���v�őł��グ���B�܂��A�ł��グ��ɁA����2������1�ɏՓ˂��������ɓ]����ꍇ���l����B����2���������A�ł��グ��ꂽ�ʒu�ɖ߂��Ă����Ƃ��A���̂���݂��Ȃ��Ȃ�B����݂��Ȃ��Ȃ�O��ŏ���1�C2�̗͊w�I�G�l���M�[�̘a�͕ۑ��������̂Ƃ���ƁA����݂��Ȃ��Ȃ�������ɂ́A����2�̑��x���@�P�@�ł���A����1�͐U�����@�R�@�̒P�U�����n�߂�B
���ɁA�ł��グ��ɁA����2��������������1�ƒe���Փ˂���ꍇ���l����B�Փ˒���̏���1�̑���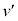 �́Av�C
�́Av�C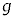 �CL��p�����@�T�@�ƕ\�����B�Փˌ�A2�̏����͎�������܂܉^�����A����1���Փˎ��̈ʒu�ɖ߂�܂ł̂��鎞��T�Ɏ��̂���݂��Ȃ��Ȃ����B���̒��ォ�炵�炭�̊ԁA���̂���݂��Ȃ��܂܉^���������������l���悤�B�܂��A����T�ɁA�����̊Ԃ̋�����L�ł���B�܂��A����݂��Ȃ��Ȃ�O��ŏ���1�C2�̗͊w�I�G�l���M�[�̘a�͕ۑ��������̂Ƃ���ƁA����T�̒���Ɏ�������܂Ȃ����߂ɂ́A����T�̒��O�ɏ���1����݂�����2�̑��x���@�V�@�łȂ���Ȃ�Ȃ��B����āA����1�ɂ͂��炭�˂̗�F�́A����T�̒��O��
�CL��p�����@�T�@�ƕ\�����B�Փˌ�A2�̏����͎�������܂܉^�����A����1���Փˎ��̈ʒu�ɖ߂�܂ł̂��鎞��T�Ɏ��̂���݂��Ȃ��Ȃ����B���̒��ォ�炵�炭�̊ԁA���̂���݂��Ȃ��܂܉^���������������l���悤�B�܂��A����T�ɁA�����̊Ԃ̋�����L�ł���B�܂��A����݂��Ȃ��Ȃ�O��ŏ���1�C2�̗͊w�I�G�l���M�[�̘a�͕ۑ��������̂Ƃ���ƁA����T�̒���Ɏ�������܂Ȃ����߂ɂ́A����T�̒��O�ɏ���1����݂�����2�̑��x���@�V�@�łȂ���Ȃ�Ȃ��B����āA����1�ɂ͂��炭�˂̗�F�́A����T�̒��O��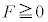 �ł���(�����������𐳂Ƃ���)�B����A����T�ɂ͎��̂���݂��Ȃ����ߒ��͂�0�ȏ�ł��邪�A���̂Ƃ�
�ł���(�����������𐳂Ƃ���)�B����A����T�ɂ͎��̂���݂��Ȃ����ߒ��͂�0�ȏ�ł��邪�A���̂Ƃ�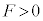 �Ȃ�Β���Ɏ��������ł��܂��B�ȏ�̂��Ƃ��A���܍l���Ă���^���ɂ����ẮA����T�ɏ���1�̈ʒu���@�X�@�łȂ���Ȃ�Ȃ��B2�̏����̗͊w�I�G�l���M�[���A�Փˌォ�玞��T�̊Ԃ͂��ꂼ��ۑ����邱�Ƃ��l����ƁA����ꂽ�������ł��グ�̑���v�́Am�C
�Ȃ�Β���Ɏ��������ł��܂��B�ȏ�̂��Ƃ��A���܍l���Ă���^���ɂ����ẮA����T�ɏ���1�̈ʒu���@�X�@�łȂ���Ȃ�Ȃ��B2�̏����̗͊w�I�G�l���M�[���A�Փˌォ�玞��T�̊Ԃ͂��ꂼ��ۑ����邱�Ƃ��l����ƁA����ꂽ�������ł��グ�̑���v�́Am�C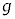 �Ck�CL��p���ĕ\�����W��
�Ck�CL��p���ĕ\�����W��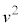 = �@�Z�@�������Ƃ��킩��B
= �@�Z�@�������Ƃ��킩��B
 ��1�@�������m���e���Փ˂���������
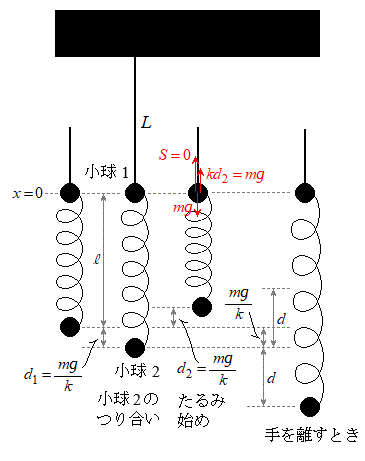
��1�@�������m���e���Փ˂���������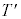 �Ƃ���B�}4�����ɕ`���ʂ��A����0����T�܂ł́A�����̑��x��\���O���t��`���B�Ȃ��A����1�������ŁA����2���d���ŕ\�����ƂƂ���B�}4�Ɏ�����Ă���l�ȊO�ɁA���x�⎞�Ԃ̒l������������K�v�͂Ȃ��B
�Ƃ���B�}4�����ɕ`���ʂ��A����0����T�܂ł́A�����̑��x��\���O���t��`���B�Ȃ��A����1�������ŁA����2���d���ŕ\�����ƂƂ���B�}4�Ɏ�����Ă���l�ȊO�ɁA���x�⎞�Ԃ̒l������������K�v�͂Ȃ��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@[�L]�C[�V]�C[�X]�ȂǁA�����ȓ_��[���n�l���Ȃ�������Ȃ����ł��B
 (1) �P�U���̒��S�͂荇���̈ʒu�ł��B�˂̎��R������̂̂т�
(1) �P�U���̒��S�͂荇���̈ʒu�ł��B�˂̎��R������̂̂т�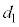 �Ƃ��āA�d�͂ƒe���͂��荇������A
�Ƃ��āA�d�͂ƒe���͂��荇������A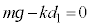 �@��
�@�� 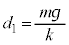 �@����@
�@����@����2�̐U�����S�̈ʒu�́A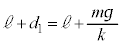 ......[�A]��𗣂����ʒu���U���[�ƂȂ�A�U���́A�U���[�ƐU�����S�Ƃ̋����ŁAd ......[�C]����1�ɓ����͂́A���̒���S(�����)�C�d��
......[�A]��𗣂����ʒu���U���[�ƂȂ�A�U���́A�U���[�ƐU�����S�Ƃ̋����ŁAd ......[�C]����1�ɓ����͂́A���̒���S(�����)�C�d��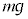 (������)�C�˂̏k�݂�
(������)�C�˂̏k�݂�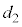 �Ƃ��āA�e����
�Ƃ��āA�e����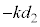 (�����)�C���������ł��Ȃ��Ƃ��̂荇�����A
(�����)�C���������ł��Ȃ��Ƃ��̂荇�����A 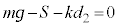 �@��
�@�� 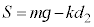
��������ޏu�Ԃ�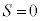 �ƂȂ�A�˂̏k�݂́A
�ƂȂ�A�˂̏k�݂́A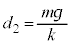 �@����A
�@����A
����ݎn�߂�Ƃ��̏���2�̈ʒu�́A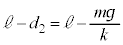 ......[�E]����2�̒P�U���ɂ����āA��𗣂����ʒu�Ƃ͋t�̐U���[(�U�����S����U��d������)�̈ʒu
......[�E]����2�̒P�U���ɂ����āA��𗣂����ʒu�Ƃ͋t�̐U���[(�U�����S����U��d������)�̈ʒu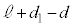 ���A[�E]����ɗ������ނ̂�(���W���͉�������������)�A
���A[�E]����ɗ������ނ̂�(���W���͉�������������)�A �� 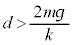 ......[�G]��������ݎn�߂�܂ŁA����1��
......[�G]��������ݎn�߂�܂ŁA����1��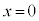 �ɐÎ~���Ă��āA����2�͒P�U�����Ă��܂��B��𗣂����Ƃ��̏���2�̒e���́{�d�͂��ʒu�G�l���M�[��
�ɐÎ~���Ă��āA����2�͒P�U�����Ă��܂��B��𗣂����Ƃ��̏���2�̒e���́{�d�͂��ʒu�G�l���M�[��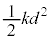 (�荇���̈ʒu����̕ψʂ��l���܂�)�C��������ޏu�ԂɁA���̂Ƃ��̏���2�̑�����
(�荇���̈ʒu����̕ψʂ��l���܂�)�C��������ޏu�ԂɁA���̂Ƃ��̏���2�̑�����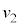 �Ƃ��ĉ^���G�l���M�[��
�Ƃ��ĉ^���G�l���M�[��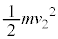 �C����2�͂荇���̈ʒu���
�C����2�͂荇���̈ʒu���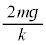 �ψʂ��Ă���([�E]��莩�R���̈ʒu���
�ψʂ��Ă���([�E]��莩�R���̈ʒu���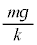 ������)�̂ŁA�e���́{�d�͂̈ʒu�G�l���M�[��
������)�̂ŁA�e���́{�d�͂̈ʒu�G�l���M�[��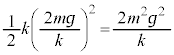 �C��𗣂����Ƃ��Ǝ�������ޏu�ԂƂ��͊w�I�G�l���M�[�ۑ����A
�C��𗣂����Ƃ��Ǝ�������ޏu�ԂƂ��͊w�I�G�l���M�[�ۑ����A 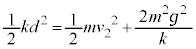 �@��
�@�� 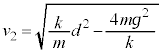 �@����B
�@����B���̂Ƃ��̏���1�̑�����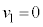 �Ȃ̂ŁA�d�S�̑����́A
�Ȃ̂ŁA�d�S�̑����́A 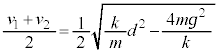 ......[�I]
......[�I]��蕶�ɂ���ʂ�A��������ݎn�߂��Ȍ�́A�d�S�����������グ�^���A���Έʒux�͒P�U�����܂�(��蕶������킵���̂Œ���)�B
����1���^���������́A����1�̉����x��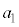 �Ƃ���(�˂̏k�݂�
�Ƃ���(�˂̏k�݂�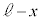 �ŏ�����̒e����
�ŏ�����̒e����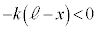 )�A
)�A 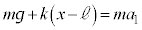 �@����C
�@����C����2�̉^���������́A����2�̉����x��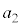 �Ƃ���(�e���͉͂������ŁA
�Ƃ���(�e���͉͂������ŁA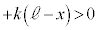 )�A
)�A 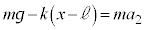 �@����D
�@����D�C�{�D�Ƃ���ƁA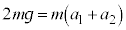 �ƂȂ�A�d�S�̉����x�́A
�ƂȂ�A�d�S�̉����x�́A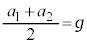
�D�|�C�Ƃ���ƁA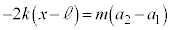 �C���Ή����x�́A
�C���Ή����x�́A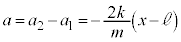
������A���Έʒux�́A�p�U����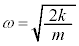 �̒P�U���ƂȂ�܂�(���Ή^�����Q��)�B���̎����́A
�̒P�U���ƂȂ�܂�(���Ή^�����Q��)�B���̎����́A 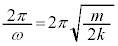 ......[�J]
......[�J]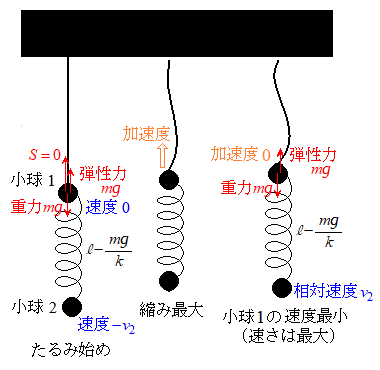 ��������ݎn�߂��Ƃ��A�˂̏k�݂͇A���
��������ݎn�߂��Ƃ��A�˂̏k�݂͇A���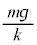 �ŏ���1�̑��x��0�C�Ȍ�A����1�ɓ����͂́A�k�˂�����1��������ɉ����͂̑傫�����������̏d�͂̑傫��������A����1�͏�����ɉ�������܂�(����1�̏�����̑����͑��傷�邪�A���x�͕��ɂȂ茸�����A�����x�͕�)�B�˂��ł��k�Ƃ��납��L�юn�߁A�˂̏k�݂�
�ŏ���1�̑��x��0�C�Ȍ�A����1�ɓ����͂́A�k�˂�����1��������ɉ����͂̑傫�����������̏d�͂̑傫��������A����1�͏�����ɉ�������܂�(����1�̏�����̑����͑��傷�邪�A���x�͕��ɂȂ茸�����A�����x�͕�)�B�˂��ł��k�Ƃ��납��L�юn�߁A�˂̏k�݂�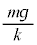 �ƂȂ�e���͂Əd�͂��荇�����u�ԂɁA����1�̉����x��0�ƂȂ菬���̑��x���ŏ��l���Ƃ�܂��B
�ƂȂ�e���͂Əd�͂��荇�����u�ԂɁA����1�̉����x��0�ƂȂ菬���̑��x���ŏ��l���Ƃ�܂��B
��������ݎn�߂��Ƃ��A�˂̏k�݂�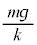 �ŏ���1�̑��x��0�C�B��
�ŏ���1�̑��x��0�C�B��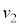 ��p���ď���2�̑��x�͏������
��p���ď���2�̑��x�͏������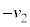 �C����1���猩�����Α��x��
�C����1���猩�����Α��x��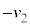 �ł��B����1�̑��x���ŏ��ɂȂ�Ƃ��A�˂̏k�݂�
�ł��B����1�̑��x���ŏ��ɂȂ�Ƃ��A�˂̏k�݂�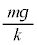 �ƂȂ肽��ݎn�߂��Ƃ��ɖ߂�̂ŁA���Έʒux���P�U�����Ă��邱�Ƃ���A���Α��x�́A����ݎn�߂��Ƃ��ƌ�����ς��A�傫���͓�����
�ƂȂ肽��ݎn�߂��Ƃ��ɖ߂�̂ŁA���Έʒux���P�U�����Ă��邱�Ƃ���A���Α��x�́A����ݎn�߂��Ƃ��ƌ�����ς��A�傫���͓�����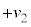 �ƂȂ�܂��B����́A[�I]��2�{�ł��B2 ......[�L]
�ƂȂ�܂��B����́A[�I]��2�{�ł��B2 ......[�L]
(2) ����1�ɂ͒��͂��������A�@�Ɠ��l�ɏ���1�ɓ����͂��荇���Ƃ��A�˂�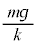 �L�т�̂ŁA���̂Ƃ��̏���1�̈ʒu�́A
�L�т�̂ŁA���̂Ƃ��̏���1�̈ʒu�́A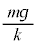 ......[�N]
......[�N] �ł��グ��ɏՓ˂��Ȃ��ꍇ�A����2���ł��グ��ꂽ�ʒu�ɖ߂肽��݂��Ȃ��Ȃ钼�O�A����2�͉������ɑ���v�ŗ������܂��B����݂��Ȃ��Ȃ钼��A����1�̑��x��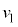 �C����2�̑��x��
�C����2�̑��x��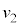 �Ƃ���ƁA����݂��Ȃ��Ȃ�O��ł̗͊w�I�G�l���M�[�ۑ����A
�Ƃ���ƁA����݂��Ȃ��Ȃ�O��ł̗͊w�I�G�l���M�[�ۑ����A 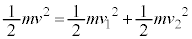 �@����E
�@����E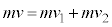 �@����F
�@����F�F���A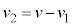 �C�E�ɑ�����A
�C�E�ɑ�����A 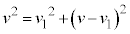 �C
�C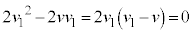
����1�͒P�U�����n�߂�̂ŁA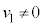 �C����āA
�C����āA 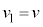 �C
�C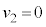
����݂��Ȃ��Ȃ�������̏���2�̑��x�́A0 ......[�P]
���D����1�Ə���2�̎��ʂ��������̂ŁA�e���Փ˂̏ꍇ�Ɠ��l�ɑ��x�̌������N����܂��B
����1�́A����݂��Ȃ��Ȃ�������(�U�����S)�ƒP�U���ʼn��_�Ƃ̗͊w�I�G�l���M�[�ۑ����A���߂�U����A�Ƃ��āA
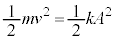 �@��
�@�� 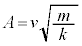 ......[�R]
......[�R]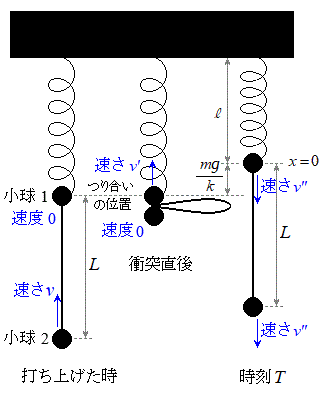 �ł��グ��ɒe���Փ˂���ꍇ�A����2�̏Փ˒��O�̑�����
�ł��グ��ɒe���Փ˂���ꍇ�A����2�̏Փ˒��O�̑�����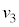 �Ƃ��āA�ł��グ���Ƃ��ƏՓ˒��O�Ƃ̗͊w�I�G�l���M�[�ۑ����A
�Ƃ��āA�ł��グ���Ƃ��ƏՓ˒��O�Ƃ̗͊w�I�G�l���M�[�ۑ����A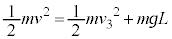 �@��
�@�� 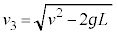
�Փ˒���̏���2�̑��x��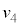 �Ƃ���(����1�̑��x��
�Ƃ���(����1�̑��x��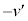 )�A�ՓˑO��ł̉^���ʕۑ����A
)�A�ՓˑO��ł̉^���ʕۑ����A 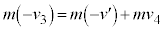 �@����G
�@����G�� 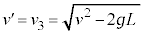 ......[�T]�܂��A
......[�T]�܂��A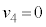 �ƂȂ�A�Փ˒��ォ�珬��2�͎��R�������܂��B���̂���݂��Ȃ��Ȃ鎞��T�̒��O�ɁA���͐L�тȂ��̂ŁA����2�̑���������1�̑������傫���Ȃ邱�Ƃ͂���܂���B�܂��A����1�̑���������2�̑������傫���Ȃ�Ǝ��͂����ł��܂��܂��B�]���āA����1�Ə���2�̑����͓����������������ŁA����1����݂�����2�̑��x�́A0 ......[�V]�܂�A����1�̑��x�͉������Ȃ̂ŁA����2�̑��x���������A����2�ɂ͏d��
�ƂȂ�A�Փ˒��ォ�珬��2�͎��R�������܂��B���̂���݂��Ȃ��Ȃ鎞��T�̒��O�ɁA���͐L�тȂ��̂ŁA����2�̑���������1�̑������傫���Ȃ邱�Ƃ͂���܂���B�܂��A����1�̑���������2�̑������傫���Ȃ�Ǝ��͂����ł��܂��܂��B�]���āA����1�Ə���2�̑����͓����������������ŁA����1����݂�����2�̑��x�́A0 ......[�V]�܂�A����1�̑��x�͉������Ȃ̂ŁA����2�̑��x���������A����2�ɂ͏d��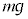 ���������Ȃ��̂ɁA����1������2�ɒǂ����Ă���Ƃ������Ƃ́A����1�ɓ����d��
���������Ȃ��̂ɁA����1������2�ɒǂ����Ă���Ƃ������Ƃ́A����1�ɓ����d��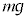 �ȊO�̗́A���Ȃ킿�e����F��
�ȊO�̗́A���Ȃ킿�e����F��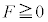 �ƂȂ�͂��ł��B�������A
�ƂȂ�͂��ł��B�������A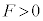 �ł́A����2�ɂ͏d��
�ł́A����2�ɂ͏d��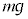 ���������Ȃ��̂ɁA����1�ɂ͏d��
���������Ȃ��̂ɁA����1�ɂ͏d��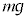 �ɉ����Ă˂̉������̒e����F���������ƂɂȂ�A����T�Ȍ�A����1�̑���������2�̑��������傫���Ȃ�A���������ł��܂��܂��B�]���āA
�ɉ����Ă˂̉������̒e����F���������ƂɂȂ�A����T�Ȍ�A����1�̑���������2�̑��������傫���Ȃ�A���������ł��܂��܂��B�]���āA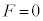 �C����āA�˂̒����͎��R���ŁA����T�ɏ���1�̈ʒu��
�C����āA�˂̒����͎��R���ŁA����T�ɏ���1�̈ʒu��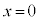 ......[�X]����2�𓊂��グ��Ƃ��A����2�̉^���G�l���M�[��
......[�X]����2�𓊂��グ��Ƃ��A����2�̉^���G�l���M�[��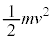 �C�d�͂̈ʒu�G�l���M�[��
�C�d�͂̈ʒu�G�l���M�[��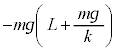 �C����1�̒e���́{�d�͂̃G�l���M�[��0�C����T�Ɏ��̂���݂��Ȃ��Ȃ����Ƃ��A����1�Ə���2�̑�����
�C����1�̒e���́{�d�͂̃G�l���M�[��0�C����T�Ɏ��̂���݂��Ȃ��Ȃ����Ƃ��A����1�Ə���2�̑�����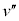 �Ƃ���([�V]��藼�҂̑��x�͓�����)�A�^���G�l���M�[�͂Ƃ���
�Ƃ���([�V]��藼�҂̑��x�͓�����)�A�^���G�l���M�[�͂Ƃ���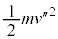 �C����1�̒e���́{�d�͂̈ʒu�G�l���M�[��
�C����1�̒e���́{�d�͂̈ʒu�G�l���M�[��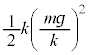 �C����2�̏d�͂̈ʒu�G�l���M�[��
�C����2�̏d�͂̈ʒu�G�l���M�[��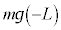
�����ŁA����2�̏Փ˒���Ǝ���T�Ƃ̗͊w�I�G�l���M�[�ۑ����(�E��}���Q��)�A 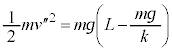 �@����H
�@����H�e���Փ˂ɂ����Ă͗͊w�I�G�l���M�[�͕ۑ������̂ŁA����2�𓊂��グ���Ƃ��Ǝ���T�Ƃ̗͊w�I�G�l���M�[�ۑ����(�E��}�Q��)�A
�H�������āA
�� 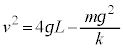 ......[�Z]
......[�Z] 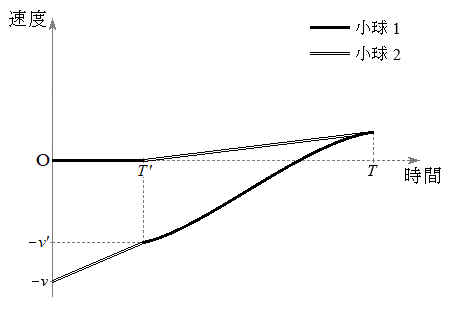
��1 �E�}
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 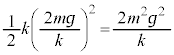 �C��𗣂����Ƃ��Ǝ�������ޏu�ԂƂ��͊w�I�G�l���M�[�ۑ����A
�C��𗣂����Ƃ��Ǝ�������ޏu�ԂƂ��͊w�I�G�l���M�[�ۑ����A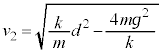 �@����B
�@����B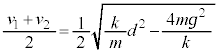 ......[�I]
......[�I]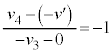 �@��
�@�� 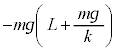 �C����1�̒e���́{�d�͂̃G�l���M�[��0�C����T�Ɏ��̂���݂��Ȃ��Ȃ����Ƃ��A����1�Ə���2�̑�����
�C����1�̒e���́{�d�͂̃G�l���M�[��0�C����T�Ɏ��̂���݂��Ȃ��Ȃ����Ƃ��A����1�Ə���2�̑�����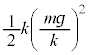 �C����2�̏d�͂̈ʒu�G�l���M�[��
�C����2�̏d�͂̈ʒu�G�l���M�[��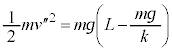 �@����H
�@����H