���s��w 2021 �N�O������������� �y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
[1] �@ ���̕��͂�ǂ�ŁA 1 �ł́A�w���ɂ��������āA�����ꂼ��̉��ɋL������B�������A�d�͉����x�̑傫���� (1) �} 1(a) �̂悤�ɁA���� m �̏������A�����x�̑傫�� V �C�n�\���������Ɋp�x θ �œ����グ��B�����͍ő卂�x A �̍��x h �ɂ����āA���� M �̃{�[���ƈꎟ���I�ɏՓ˂����A���̔����𗘗p���ď������������ˏグ��B�����ŁA�ꎟ���I�ɏՓ˂���Ƃ́A�} 1(b) �̂悤�ɏՓ˒��O����̏����ƃ{�[�������꒼����ɉ����ĉ^�����邱�Ƃ������A���̒����ɉ����Փˎ����`����B�Փˎ��͏Փ˒��O�̃{�[���̐i�s�����𐳂Ƃ��A�Փˎ������̑��x�������A�ȉ������āu���x�����v�ƋL�ڂ���B�Ȃ��A�Փ˂͏u�ԓI�ɋN������̂Ƃ��A�����ƃ{�[���̑傫���A����ы�C��R�̉e���͖�������B �} 1(b) �̂悤�ɁA�Փ˒��O�̏����ɂ��āA���̑��x�̑傫���� V �C θ �C h �C �@��� (i) �����ŁA m �C M �C����� �@��� (ii) �����藧�̂ŁA�� (i) �C (ii) ���A�Փ˒���̑��x���� m �C M ��p���� M �������̎��� m �� 0 �ƂȂ�A�Փ˒���̏����̑��x���� h �C V �C θ �C (2) (1) �̏���������ɍ������ˏグ�邽�߁A�} 2 �̂悤�ɁA�ő卂�x�ɓ��B������ɗ������Ă��鏬���߂����āA���x h �Ń{�[�����Փ˂�����A�Ƃ����ߒ����J��Ԃ��s�Ȃ����Ƃ��悤�B�����ŁA (1) �Ɠ��l�ɁA�����ƃ{�[���͈ꎟ���I�ɏՓ˂��A�} 3 �̂悤�ɏՓ˂��Ƃɒ�`�����Փˎ������̑��x�������A�ȉ������āu���x�����v�ƋL�ڂ���B�܂� n ��� ( �̏Փˎ��̃{�[���́A�Փ˒��O�̑��x�̑傫���� 0 �ƂȂ鎿�� ���̂Ƃ��A n ��ڂ̏Փ˒���ɂ����鏬���̑��x���� �@��� (iii) (1) ���A (iii) �������āA h �C V �C θ �C n ��p���āA �� 1 �@ (2) �ɂ�����Փˉߒ��ɂ��āA�ȉ��̖₢�ɓ�����B
(i) n ��ڂɏՓ˂�����{�[���̎��� m �̉��{�ɂ���悢���B n ��p���ĕ\���B���o�ߒ��������B (ii) �Փ˂�����{�[���̎��ʂɏ��������ƁA�Փ˒���̃{�[���̑��x������ 0 �ƂȂ�Փˉɏ�����ł���B�{�[���̎��ʂ̏���������̎��� m �� 10 �{�ł���ꍇ�A�Փˉ�����ɒB�����Ƃ��̏��������B����ő卂�x�́A�{�[���ƏՓ˂���O�̍ő卂�x [ �� ] [2] �@ ���̕��͂�ǂ�ŁA 1 �C�� 2 �ł́A�w���ɂ��������āA�����ꂼ��̉��ɋL������B�������A�~������ π �Ƃ���B 1 �̂悤�ɁA���a L �̉~�ʌ`���������� XY �ɁA���S O ���x�_�Ƃ��Ē[�_ P �ʼn~�ʂƐڂ��Ȃ����]�ł��钷�� L �̓��̖_ OP ���ڑ�����Ă���A OY �Ԃɒ�R�l R �̒�R�Ɠd�C�e�� C �̃R���f���T�[�������Őڑ�����Ă���B XY �a�Ƃ���D�F�̔��~�̈�ɁA���ʂ̗�����\�Ɍ������������x B �̈�l�Ȏ��E���������Ă���A���� P �͓_ X �̈ʒu�ɂ���B�܂��A���̖_�����̊p���x P ������ Y �ɓ��B������A���̖_��Î~�������ɏu�ԓI�ɐ܂�Ԃ��B�_ Y ���玞�v���ɓ����傫���̊p���x�ʼn�]������ƁA�[�_ P �͎��� X �ɖ߂�A���� 1 �̖��̌����ɗ����ꍇ�𐳂Ƃ��A���̖_�ɐ�����N�d�͂̕����́A���̓d���𗬂��ꍇ�𐳂Ƃ���B�܂��A��H�𗬂��d��������o������͖�������B (1) ���� P ���_ X ���瓮���n�߂��Ƃ��A��H OPYO ���т������̕ω�����A���̖_�̗��[�ɐ�����N�d�͂� ���̖_���_ Y �Ɍ������ĉ�]���Ă���Ƃ��A���� t (�ɂ����ĉ�H�𗬂��d���� I �C�R���f���T�[�ɒ~�����Ă���d�C�ʂ� Q �Ƃ���B���̂Ƃ��A�L���q�z�b�t�̑� 2 �@����� �@��� (i) �̊W������B�d�� I �́A���� I �͕ω������A 2 ���ȏ�̍��͖������邱�ƂƂ���B�������� I �C B �C L �C T ��p���� (2) ���̖_�̒[�_ P ���_ X ���o��������A Q �́A�} 2 �̃O���t�̋Ȑ��Ŏ������悤�Ȏ��ԕω����������B���̖_�̊p���x���������A�[�_ P ���_ Y �ɓ��B��������O�ɓd�����\���������Ȃ�A���� 0 �Ƃ݂Ȃ���Ƃ��A���� t �̒l�� P ���_ X ���o����������̔������Ԃɂ�����d�C�ʂ̕ω���\�����Ƃɒ��ӂ���ƁA B �C L �C T �C C �C R �̂����K�v�Ȃ��̂�p���� �� 1 �@���� P ���_ Y �ɓ��B������A�Î~�������ɏu�ԓI�ɐ܂�Ԃ��ƁA�d�����Ăї���o���A�_ X �ɓ��B��������O�ɓd���� 0 �Ƃ݂Ȃ����ԂɂȂ����Ƃ���B Q �̎��ԕω����A���� 2 �Ɠ��l�ɕ`���B (3) ���ɁA���̖_�̊p���x���傫���A���� P ���_ Y �ɓ��B�����Ƃ��ɓd���� 0 �Ƃ݂Ȃ��Ȃ��ꍇ���l����B ���� t �ɂ����ăR���f���T�[�ɒ~�����Ă���d�C�ʂ� 2 �@���� �@��� (ii) �Ə������Ƃ��ł��A (ii) �̉��� �@��� (iii) �ƕ\�����Ƃ��ł���B�����ŁA 0 �Ƃ݂Ȃ���Ƃ��̎��� (2) ��� x ��p���� (iii) �� x ��p���āA���ꂼ�� �� 2 �@���̖_�����x�����������Ȃ���\���Ȏ��Ԃ��o�߂����Ƃ��A�R���f���T�[�ɒ~�����Ă���d�C�ʂ́A�ő�l T �� x �̒l�����߂Đ�������B [ �� ] [3] �@ ���̕��͂�ǂ�ŁA �@�@�@ �ɓK�������܂��͐��l���A���ꂼ��̉��ɋL������B�Ȃ��A �@�@�@ �͂��ł� �@�@�@ �ŗ^����ꂽ���̂Ɠ������̂�\���B�܂��A�� 1 �C�� 2 �ł́A�w���ɂ��������āA�����ꂼ��̉��ɋL������B�������A�~������ π �Ƃ���B (1) �} 1 �̂悤�ɁA X ���̌����ɂ�锽�˂��l����B�����̒��ŁA���q�͊Ԋu d �ŕ��s�ɕ��ʇT�C�U�C�V�C�����ɋK������������ł���B�܂��A X ���̔������͌�������\�����ꂽ�ꏊ�ɒu����Ă���A X ���͌����ɑ��ē����������畽�s�ɓ��˂���Ƃ��Ă悢�B���̂Ƃ��A���� X ���ƌ����ʂ̂Ȃ��p�x�� θ �Ƃ���B���q�ɂ�蔽�˂��ꂽ X ���������ʂ���p�x θ �̕����ɂ��錟�o��Ō��o����B���o�����������\�����ꂽ�ꏊ�ɂ���A���o��Ŋϑ����锽�� X ���͑S�ĕ��s�ł���Ƃ��Ă悢�B�����ŁA θ �� 0 ���� X ���̔g���� λ �Ƃ���B
�} 2 �Ɏ����悤�ɁA�����ʇT��ɂ��錴�q P �ƁA���̈�w���̌����ʇU��ɂ��錴�q Q �ɂ�� X ���̔��˂��l����B���q Q �͌��q P �̒����ɂ�����̂Ƃ���B���̂Ƃ��A 2 �� X ���̌o�H���� d ����� θ ��p���� �@���@ �ƕ\�����B�]���āA 2 �� X �������ߍ������߂̏������́A k �𐳂̐����Ƃ��Ĕg�� λ �C�Ԋu d �C����ъp�x θ ��p���� �@���@ �ŕ\�����B (2) ���q�� X ���̊Ԃɂ͂��炭�͂ɂ��A X ���̋O���͌������ɓ���Ƃ킸���Ȃ���ω�����B��������ܗ��̌`�ŕ\���ƁA�������̋��ܗ� n �� 1 ��育���킸���ɏ������l�����B�܂��A X ���̋�C���̋��ܗ��� 1 �ł���Ƃ���B���ܗ����l������� (1) �ŋ��߂����������ǂ̂悤�ɕύX����邩�l�@���悤�B�} 2 �Ɠ��l�ɁA�����ʇT��ɂ��錴�q P �ƁA���̈�w���̌����ʇU��ɂ��錴�q Q �ɂ�� X ���̔��˂��l����B�������A X ���͑S���˂��N����Ȃ��p�x�œ��˂�����̂Ƃ���B���̂Ƃ��A�������ł� X ���̔g�����ω����A�} 3 �ɕ`����Ă���悤�Ɍ��q Q �ɂ͊p�x θ ��菬�����p�x X �������˂��邱�ƂɂȂ邪�A �@���@ �Ƃ����W�������藧�B�܂��A�������̔g���� λ �ƌ������̋��ܗ� n ��p���� �@���@ �ŕ\�����B�]���āA 2 �� X ���̈ʑ��̍��́A d �C λ �C n �C θ ��p���� �@���@ �ƕ\�����B�������A X ���̔������ɂ����� 2 �� X ���̏����ʑ��͓����ł�����̂Ƃ���B�܂��A �@���@ �� X �������ߍ����Ƃ�����������A 2 �� X �������ߍ������߂̏������́A d �C λ �C n �C θ �C���̐��� k ��p���� �@���@ �ŕ\�����B (3) �d�q�⒆���q�Ȃǂ̗��q�́A�g���̐������������Ƃ��m���Ă���B������h�E�u���C�g ( �����g ) �Ƃ����A���̔g�� λ �͗��q�̎��ʂ� m �C������ v �Ƃ��� �ŗ^������B�����ŁA h �̓v�����N�萔�ƌĂ��萔�ł���B�h�E�u���C�g�͎��� T �C�g�� λ �̐����g�ŕ\���A���q�������ɓ��˂���� X ���̂Ƃ��̂悤�ɉ�܂⊱���N����B 4 �Ɏ����悤�� xy ���ʂ������ʁA z �����������d�͂̌����ƂȂ�悤�������W�����Ƃ�A�d�͉����x�̑傫���� g �Ƃ���B���� Σ �́A�����ʂƌ���钼���� y ���ƕ��s�ƂȂ镽�ʂł���A���̒��������ɂ��ĉ�]�ł�����̂Ƃ���B���� Σ �������ʂƂȂ��p�� α �Ƃ��� ( �} 4 �̊p�x�̌����𐳂Ƃ��� ) �B���� Σ ���ɕ��s�l�ӌ` ABCD �C�����ē_ E �C N �����݂��A�� AB �͐����ʏ�ɂ���B�_ N �C A �C B ����ѓ_ D �C C �C E �́A���ꂼ�ꓯ��������ɂ���A�� AB �ƕ� DC �̊Ԋu�� s �ł��� ( �} 5 �Q�� ) �B Σ ���̏ڍׂ�} 5 �Ɏ����B�����ŁA�����q�����s�l�ӌ` ABCD ��̕ӂ��^������悤�A�K���Ȍ�����_ A �C B �C C �C D �ɓK�Ȋp�x�Ŕz�u���A�_ N �ɂ��钆���q������_ A �ɑ��� m �Ƃ��A���˂���h�E�u���C�g�̔g���� (1) �ŋ��߂����˂̏����������������̂Ƃ���B������ 2 �ɕ����ꂽ�����q�̔g���ēx 2 �̌�����̓_ B ����� D �Ŕ��˂����邱�Ƃɂ��A�_ C �ɏW���A�_ E �Ńh�E�u���C�g���ϑ�����B ABCD �������ʂɑ��Đ����ɂȂ�ꍇ���l����B�����q���� DC ���Ƃ��́A������ s ��p����ƁA�g���� �@���@ �ƂȂ�B �@���@ �� 2 �̈قȂ�o�H�ɂ��h�E�u���C�g�̊������邱�Ƃɂ��A�����q�ɑ���d�͂̉e�����ϑ����邱�Ƃ��ł���B �� 1 �@ AB �̒����� ABCE ��ʂ�ꍇ�ƌo�H ADCE ��ʂ�ꍇ�ŁA�����g�̈ʑ��̍������߁A m �C s �C h �C T �� 2 �̌o�H�ŕω������A�ʑ��̍��͔g���̈Ⴂ�݂̂Ō��܂�B����ɁA 1 ���\���ɏ������Ƃ��ɐ��藧�ߎ��� ��p���Ă��悢�B
�� 2 �@ (i) �} 4 �̊p�x α ��ω������Ȃ���_ E �Œ����q�r�[�����x���ϑ����邱�Ƃɂ��A�d�͂̉e�����݂邱�Ƃ��ł���B�p�x α �� 0 ���� E �Œ����q�r�[�������ɂ�苭�ߍ������Ƃ�����N���邩������B (ii) �p�x α �� 0 ���瑝���������Ƃ��A�_ E �Œ����q�r�[�����͂��߂Ċ��ɂ���ߍ����Ƃ��� 2 �����œ�����B [ �� ] �y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@ ���啨�� TOP �@�@ ���� TOP �@�@ TOP �y�[�W�ɖ߂� �y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B �e���̒��쌠�� © 2005-2024 (�L)����� ��w�y�w�m ���������t���I ���n��w�l�b�g�m ��w�y�w�m (���ē��������� )������́A������܂Ń��[�� �� 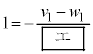 �@���(ii)
�@���(ii)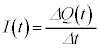 �C���̖_�ɐ�����N�d�͂�
�C���̖_�ɐ�����N�d�͂�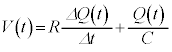 �@���(ii)
�@���(ii)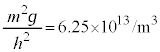 �C
�C