���啨��'21�N�O��[2]
���̕��͂�ǂ�ŁA �ɓK�������܂��͐��l���A���ꂼ��̉��ɋL������B�Ȃ��A
�ɓK�������܂��͐��l���A���ꂼ��̉��ɋL������B�Ȃ��A �͂��ł�
�͂��ł� �ŗ^����ꂽ���̂Ɠ������̂�\���B�܂��A��1�C��2�ł́A�w���ɂ��������āA�����ꂼ��̉��ɋL������B�������A�~������π�Ƃ���B
�ŗ^����ꂽ���̂Ɠ������̂�\���B�܂��A��1�C��2�ł́A�w���ɂ��������āA�����ꂼ��̉��ɋL������B�������A�~������π�Ƃ���B
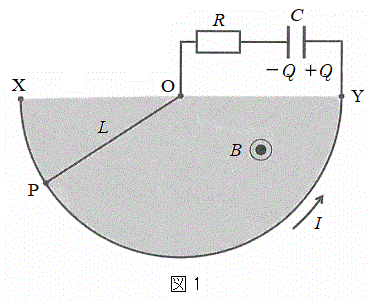 �}1�̂悤�ɁA���aL�̉~�ʌ`����������XY�ɁA���SO���x�_�Ƃ��Ē[�_P�ʼn~�ʂƐڂ��Ȃ����]�ł��钷��L�̓��̖_OP���ڑ�����Ă���AOY�Ԃɒ�R�lR�̒�R�Ɠd�C�e��C�̃R���f���T�[�������Őڑ�����Ă���BXY�a�Ƃ���D�F�̔��~�̈�ɁA���ʂ̗�����\�Ɍ������������xB�̈�l�Ȏ��E���������Ă���A����
�}1�̂悤�ɁA���aL�̉~�ʌ`����������XY�ɁA���SO���x�_�Ƃ��Ē[�_P�ʼn~�ʂƐڂ��Ȃ����]�ł��钷��L�̓��̖_OP���ڑ�����Ă���AOY�Ԃɒ�R�lR�̒�R�Ɠd�C�e��C�̃R���f���T�[�������Őڑ�����Ă���BXY�a�Ƃ���D�F�̔��~�̈�ɁA���ʂ̗�����\�Ɍ������������xB�̈�l�Ȏ��E���������Ă���A����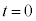 �ɂ����ē��̖_�̒[�_P�͓_X�̈ʒu�ɂ���B�܂��A���̖_�����̊p���x
�ɂ����ē��̖_�̒[�_P�͓_X�̈ʒu�ɂ���B�܂��A���̖_�����̊p���x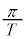 �Ŕ����v���ɉ�]������B�[�_P������
�Ŕ����v���ɉ�]������B�[�_P������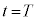 �œ_Y�ɓ��B������A���̖_��Î~�������ɏu�ԓI�ɐ܂�Ԃ��B�_Y���玞�v���ɓ����傫���̊p���x�ʼn�]������ƁA�[�_P�͎���
�œ_Y�ɓ��B������A���̖_��Î~�������ɏu�ԓI�ɐ܂�Ԃ��B�_Y���玞�v���ɓ����傫���̊p���x�ʼn�]������ƁA�[�_P�͎���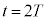 �œ_X�ɖ߂�A����
�œ_X�ɖ߂�A����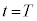 �̂Ƃ��Ɠ��l�ɏu�ԓI�ɐ܂�Ԃ��B����
�̂Ƃ��Ɠ��l�ɏu�ԓI�ɐ܂�Ԃ��B����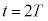 �ȍ~�́A
�ȍ~�́A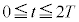 �̓��̖_�̉^�����J��Ԃ��Ƃ���B�����A���̖_�A�~�ʂ̐ړ_�ɂ������R�͖����ł���Ƃ��A����
�̓��̖_�̉^�����J��Ԃ��Ƃ���B�����A���̖_�A�~�ʂ̐ړ_�ɂ������R�͖����ł���Ƃ��A����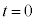 �ɂ����ăR���f���T�[�ɓd�ׂ͒~�����Ă��Ȃ��������̂Ƃ���B�d���̕����͐}1�̖��̌����ɗ����ꍇ�𐳂Ƃ��A���̖_�ɐ�����N�d�͂̕����́A���̓d���𗬂��ꍇ�𐳂Ƃ���B�܂��A��H�𗬂��d��������o������͖�������B
�ɂ����ăR���f���T�[�ɓd�ׂ͒~�����Ă��Ȃ��������̂Ƃ���B�d���̕����͐}1�̖��̌����ɗ����ꍇ�𐳂Ƃ��A���̖_�ɐ�����N�d�͂̕����́A���̓d���𗬂��ꍇ�𐳂Ƃ���B�܂��A��H�𗬂��d��������o������͖�������B
(1) ����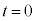 �œ��̖_�̒[�_P���_X���瓮���n�߂��Ƃ��A��HOPYO���т������̕ω�����A���̖_�̗��[�ɐ�����N�d�͂�
�œ��̖_�̒[�_P���_X���瓮���n�߂��Ƃ��A��HOPYO���т������̕ω�����A���̖_�̗��[�ɐ�����N�d�͂� �Ƌ��߂���B��H�ɂ͓d��
�Ƌ��߂���B��H�ɂ͓d�� ������o���A�R���f���T�[�ɂ͓d�ׂ��~�����n�߂�B
������o���A�R���f���T�[�ɂ͓d�ׂ��~�����n�߂�B ���̖_���_Y�Ɍ������ĉ�]���Ă���Ƃ��A����t (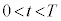 )�ɂ����ĉ�H�𗬂��d����I�C�R���f���T�[�ɒ~�����Ă���d�C�ʂ�Q�Ƃ���B���̂Ƃ��A�L���q�z�b�t�̑�2�@�����
)�ɂ����ĉ�H�𗬂��d����I�C�R���f���T�[�ɒ~�����Ă���d�C�ʂ�Q�Ƃ���B���̂Ƃ��A�L���q�z�b�t�̑�2�@����� 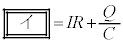 �@���(i)
�@���(i)�̊W������B�d��I�́A����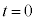 �̂Ƃ��̓d��
�̂Ƃ��̓d�� �����������B���̖_�͉�]�����Ɣ��Ό����Ɏ��E����͂��邽�߁A���̖_�����̊p���x�ʼn�]���������邽�߂ɂ́A�O������d����^���Ȃ���Ȃ�Ȃ��B���܁A��������
�����������B���̖_�͉�]�����Ɣ��Ό����Ɏ��E����͂��邽�߁A���̖_�����̊p���x�ʼn�]���������邽�߂ɂ́A�O������d����^���Ȃ���Ȃ�Ȃ��B���܁A��������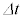 �̊ԂɃR���f���T�[�ɒ~������d�C�ʂ�
�̊ԂɃR���f���T�[�ɒ~������d�C�ʂ�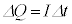 �������������Ƃ���B�������A��������
�������������Ƃ���B�������A��������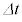 �̊Ԃɓd��I�͕ω������A
�̊Ԃɓd��I�͕ω������A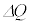 �C
�C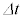 ��2���ȏ�̍��͖������邱�ƂƂ���B��������
��2���ȏ�̍��͖������邱�ƂƂ���B��������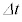 �̊Ԃɒ�R�ŏ�����W���[���M��
�̊Ԃɒ�R�ŏ�����W���[���M��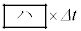 �C�R���f���T�[�ɒ~������Ód�G�l���M�[�̑����ʂ�
�C�R���f���T�[�ɒ~������Ód�G�l���M�[�̑����ʂ� �ł���B�������A
�ł���B�������A �C
�C ��
��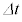 ���܂܂Ȃ����œ����邱�ƁB���̗��҂̘a�́AI�CB�CL�CT��p����
���܂܂Ȃ����œ����邱�ƁB���̗��҂̘a�́AI�CB�CL�CT��p���� �ƕ\�����Ƃ��ł��A
�ƕ\�����Ƃ��ł��A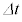 �̊ԂɊO�����瓱�̖_�ɗ^�����d���ɓ������B
�̊ԂɊO�����瓱�̖_�ɗ^�����d���ɓ������B
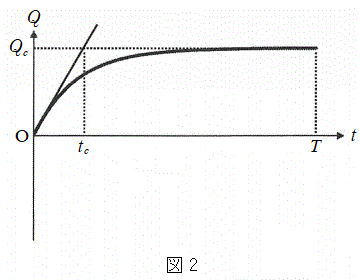 (2) ���̖_�̒[�_P���_X���o��������A
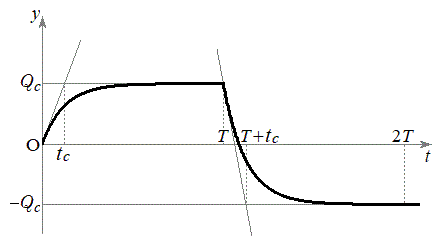
(2) ���̖_�̒[�_P���_X���o��������A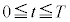 �̊Ԃɂ����ăR���f���T�[�ɒ~�����Ă���d�C��Q�́A�}2�̃O���t�̋Ȑ��Ŏ������悤�Ȏ��ԕω����������B���̖_�̊p���x���������A�[�_P���_Y�ɓ��B��������O�ɓd�����\���������Ȃ�A����
�̊Ԃɂ����ăR���f���T�[�ɒ~�����Ă���d�C��Q�́A�}2�̃O���t�̋Ȑ��Ŏ������悤�Ȏ��ԕω����������B���̖_�̊p���x���������A�[�_P���_Y�ɓ��B��������O�ɓd�����\���������Ȃ�A����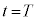 �ɂ����ēd����0�Ƃ݂Ȃ���Ƃ��A����
�ɂ����ēd����0�Ƃ݂Ȃ���Ƃ��A����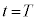 �ɂ�����d�C��
�ɂ�����d�C��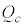 ��
�� �ł���B����
�ł���B����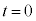 �ɂ�����Ȑ��̐ڐ���
�ɂ�����Ȑ��̐ڐ���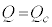 �̒����ƌ����_��t �̒l��
�̒����ƌ����_��t �̒l��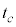 �Ƃ���B����
�Ƃ���B����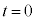 �ɂ�����ڐ��̌X�����A���̖_�̒[�_P���_X���o����������̔������Ԃɂ�����d�C�ʂ̕ω���\�����Ƃɒ��ӂ���ƁA
�ɂ�����ڐ��̌X�����A���̖_�̒[�_P���_X���o����������̔������Ԃɂ�����d�C�ʂ̕ω���\�����Ƃɒ��ӂ���ƁA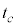 ��B�CL�CT�CC�CR�̂����K�v�Ȃ��̂�p����
��B�CL�CT�CC�CR�̂����K�v�Ȃ��̂�p����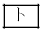 �ƕ\����B
�ƕ\����B
��1�@����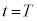 �ɂ����Ē[�_P���_Y�ɓ��B������A�Î~�������ɏu�ԓI�ɐ܂�Ԃ��ƁA�d�����Ăї���o���A�_X�ɓ��B��������O�ɓd����0�Ƃ݂Ȃ����ԂɂȂ����Ƃ���B
�ɂ����Ē[�_P���_Y�ɓ��B������A�Î~�������ɏu�ԓI�ɐ܂�Ԃ��ƁA�d�����Ăї���o���A�_X�ɓ��B��������O�ɓd����0�Ƃ݂Ȃ����ԂɂȂ����Ƃ���B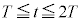 �̊Ԃɂ����ăR���f���T�[�ɒ~�����Ă���d�C��Q�̎��ԕω����A����
�̊Ԃɂ����ăR���f���T�[�ɒ~�����Ă���d�C��Q�̎��ԕω����A����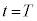 �ɂ�����ڐ��̌X����������悤�ɁA�}2�Ɠ��l�ɕ`���B
�ɂ�����ڐ��̌X����������悤�ɁA�}2�Ɠ��l�ɕ`���B
(3) ���ɁA���̖_�̊p���x���傫���A����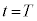 �Œ[�_P���_Y�ɓ��B�����Ƃ��ɓd����0�Ƃ݂Ȃ��Ȃ��ꍇ���l����B
�Œ[�_P���_Y�ɓ��B�����Ƃ��ɓd����0�Ƃ݂Ȃ��Ȃ��ꍇ���l����B ����t �ɂ����ăR���f���T�[�ɒ~�����Ă���d�C�ʂ�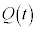 �C��H�𗬂��d����
�C��H�𗬂��d����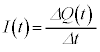 �C���̖_�ɐ�����N�d�͂�
�C���̖_�ɐ�����N�d�͂�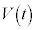 �Ƃ���ƁA�L���q�z�b�t�̑�2�@����
�Ƃ���ƁA�L���q�z�b�t�̑�2�@���� 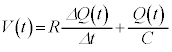 �@���(ii)
�@���(ii)�Ə������Ƃ��ł��A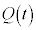 �ɂ��Ẳ������߂��邱�Ƃ��m���Ă���B���鎞���͈�
�ɂ��Ẳ������߂��邱�Ƃ��m���Ă���B���鎞���͈�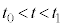 �ɂ����ē��̖_�̋N�d��
�ɂ����ē��̖_�̋N�d��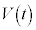 �����ł���Ƃ���ƁA
�����ł���Ƃ���ƁA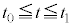 �ɂ�����
�ɂ�����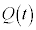 �ɂ��Ă̎�(ii)�̉���
�ɂ��Ă̎�(ii)�̉��� 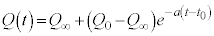 �@���(iii)
�@���(iii)�ƕ\�����Ƃ��ł���B�����ŁA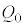 �͎���
�͎���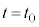 �ɂ����ăR���f���T�[�ɒ~�����Ă���d�C�ʁA
�ɂ����ăR���f���T�[�ɒ~�����Ă���d�C�ʁA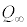 ��
��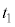 ���\���傫���A�d����0�Ƃ݂Ȃ���Ƃ��̎���
���\���傫���A�d����0�Ƃ݂Ȃ���Ƃ��̎���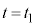 �ɂ�����d�C�ʁA
�ɂ�����d�C�ʁA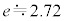 �͎��R�ΐ��̒�A
�͎��R�ΐ��̒�A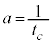 �ł���A
�ł���A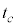 ��
��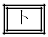 �ŕ\�����萔�ł���B
�ŕ\�����萔�ł���B
�܂��A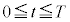 �̏ꍇ���l����B
�̏ꍇ���l����B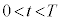 �ɂ�����
�ɂ�����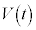 �͈��l
�͈��l �ł���̂ŁA(2)���
�ł���̂ŁA(2)���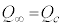 �Ƃ�����B���������āA
�Ƃ�����B���������āA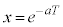 �Ƃ����ƁA����
�Ƃ����ƁA����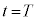 �ɂ����ăR���f���T�[�ɒ~�����Ă���d�C�ʂ́Ax��p����
�ɂ����ăR���f���T�[�ɒ~�����Ă���d�C�ʂ́Ax��p���� �ƕ\����B
�ƕ\����B
���ɁA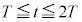 �C
�C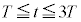 �̏ꍇ���l����ƁA���ꂼ��
�̏ꍇ���l����ƁA���ꂼ��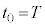 �C
�C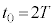 �Ƃ��āA��(iii)��
�Ƃ��āA��(iii)��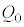 ��
��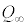 ��K���Ȏ��Œu�������A
��K���Ȏ��Œu�������A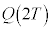 �C
�C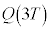 �����߂邱�Ƃ��ł���B����
�����߂邱�Ƃ��ł���B����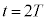 �C
�C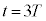 �ɂ����ăR���f���T�[�ɒ~�����Ă���d�C�ʂ́A
�ɂ����ăR���f���T�[�ɒ~�����Ă���d�C�ʂ́A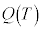 �Ɠ��l��x��p���āA���ꂼ��
�Ɠ��l��x��p���āA���ꂼ��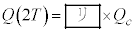 �C
�C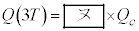 �ƕ\�����Ƃ��ł���B
�ƕ\�����Ƃ��ł���B
��2�@���̖_�����x�����������Ȃ���\���Ȏ��Ԃ��o�߂����Ƃ��A�R���f���T�[�ɒ~�����Ă���d�C�ʂ́A�ő�l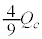 �ƍŏ��l
�ƍŏ��l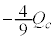 �̊Ԃŕω����A����Ɏ��Ԃ��o�߂��Ă��ő�l�ƍŏ��l�͈��̂܂܂ł������B���̏ꍇ��T��
�̊Ԃŕω����A����Ɏ��Ԃ��o�߂��Ă��ő�l�ƍŏ��l�͈��̂܂܂ł������B���̏ꍇ��T��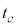 �̑召�W�ɂ��āAx�̒l�����߂Đ�������B
�̑召�W�ɂ��āAx�̒l�����߂Đ�������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���Ƃ����킯�ł͂Ȃ��A�㔼�͖�蕶��(iii)�����ǂ����p���邩�Ƃ��������ł����A�����������߂̐F�X�ȏ��������̂ŁA��蕶�̂����������m�F���Ȃ�������i�߂Ȃ�������܂���B
(1) 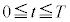 �ɂ����āA���̖_�͊p���x
�ɂ����āA���̖_�͊p���x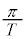 �ʼn�]����̂Ŏ���t �ł̉�]�p��
�ʼn�]����̂Ŏ���t �ł̉�]�p��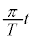 �C��`OPX�̖ʐ�S (��ʊp���Q��)�́A
�C��`OPX�̖ʐ�S (��ʊp���Q��)�́A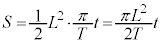 �C��`OPX���т�����Φ�́A
�C��`OPX���т�����Φ�́A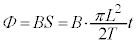 �C�U���N�d�͂́A�t�@���f�[���d���U���̖@�����A
�C�U���N�d�͂́A�t�@���f�[���d���U���̖@�����A 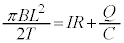 �@���(i)
�@���(i)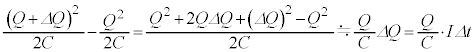 �C
�C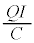 ......[�j]
......[�j]���҂̘a�́A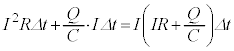 �CI�CB�CL�CT��p���ē�����̂ŁA(i)�����A
�CI�CB�CL�CT��p���ē�����̂ŁA(i)�����A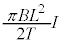 ......[�z]
......[�z]
(2) (i)����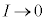 �C
�C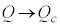 �Ƃ��āA
�Ƃ��āA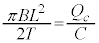 �@��
�@�� 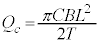 ......[�w]
......[�w]
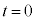 �ɂ�����(��)�̌��ʂ��A
�ɂ�����(��)�̌��ʂ��A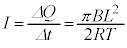 �C���ꂪ�}2�̃O���t��
�C���ꂪ�}2�̃O���t��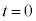 �ɂ������ڐ��̌X���B(�w)�̌��ʁA
�ɂ������ڐ��̌X���B(�w)�̌��ʁA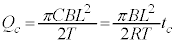 ���A
���A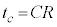 ......[�g]
......[�g]
��1�@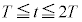 �ɂ����āA���̖_��Y����X�Ɍ������ĉ�]���܂��B�N�d�͂̌����́A�t���~���O�E��̖@�����AP��O�̌����ɓd���𗬂������ŕ��A�܂�
�ɂ����āA���̖_��Y����X�Ɍ������ĉ�]���܂��B�N�d�͂̌����́A�t���~���O�E��̖@�����AP��O�̌����ɓd���𗬂������ŕ��A�܂�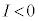 �C������A(i)���́A
�C������A(i)���́A 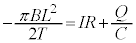 �@����@
�@����@�ƂȂ�܂��B�@��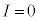 �Ƃ����(��)�̌��ʂ�p���āA
�Ƃ����(��)�̌��ʂ�p���āA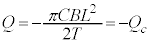 �C�d����0�ɋ߂Â��ƁA�R���f���T�[�̓d�C�ʂ�
�C�d����0�ɋ߂Â��ƁA�R���f���T�[�̓d�C�ʂ�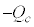 �ɋ߂Â��܂�(�R���f���T�[�̉ߓn�������Q��)�B
�ɋ߂Â��܂�(�R���f���T�[�̉ߓn�������Q��)�B
 �܂��A
�܂��A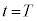 �ɂ�����(�w)���A�R���f���T�[�͓d�C��
�ɂ�����(�w)���A�R���f���T�[�͓d�C��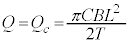 ��~���Ă���̂ŁA�@���A
��~���Ă���̂ŁA�@���A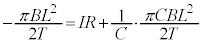 �C����ēd���́A
�C����ēd���́A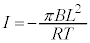 �C���ꂪ�AQ-t �O���t��
�C���ꂪ�AQ-t �O���t��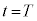 �ɂ�����ڐ��̌X��(�X���͕��ł����A��Βl��
�ɂ�����ڐ��̌X��(�X���͕��ł����A��Βl��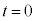 �̂Ƃ���2�{)�ɂȂ�܂��B�ڐ���
�̂Ƃ���2�{)�ɂȂ�܂��B�ڐ���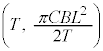 ���̒ʂ�̂ŁA�ڐ��̎��́A
���̒ʂ�̂ŁA�ڐ��̎��́A �����ŁA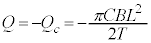 �Ƃ����(�g)�̌��ʂ�p���āA
�Ƃ����(�g)�̌��ʂ�p���āA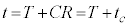 �C����āA�E�}�B
�C����āA�E�}�B
V�����ł���A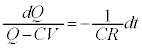 �C
�C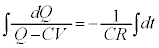
�� 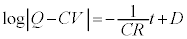 (D�F�ϕ��萔)
(D�F�ϕ��萔)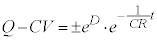 �@����A
�@����A (2)�ɂ�����(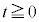 )�A
)�A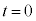 �̂Ƃ�
�̂Ƃ�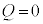 �Ƃ��āA
�Ƃ��āA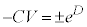 �C�A�ɑ�����āA
�C�A�ɑ�����āA 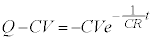 �@����B
�@����B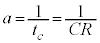 ���A
���A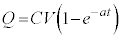 �@����C
�@����C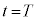 �ɂ����āA
�ɂ����āA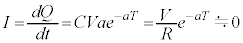 �Ƃ���ƁA
�Ƃ���ƁA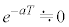 �C
�C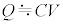
����āA�����ł�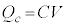 �Ƃ��ćC���A
�Ƃ��ćC���A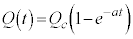
���̃O���t���}2�ł��B(3)�ɂ����ẮA�C�ɂ����āA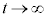 �̂Ƃ�
�̂Ƃ�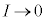 �C
�C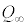 �͓d����0�Ƃ݂Ȃ���Ƃ��̓d�C�ʂȂ̂ŁA�C��
�͓d����0�Ƃ݂Ȃ���Ƃ��̓d�C�ʂȂ̂ŁA�C��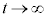 �Ƃ��āA
�Ƃ��āA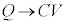 �C����āA
�C����āA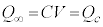 �C�C�ɓ���߂��āA
�C�C�ɓ���߂��āA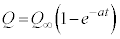
������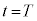 (���x�́A
(���x�́A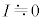 �Ƃ݂Ȃ��Ȃ��̂ŁA
�Ƃ݂Ȃ��Ȃ��̂ŁA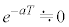 �������܂���)�Ƃ��āA
�������܂���)�Ƃ��āA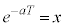 �Ƃ����ƁA
�Ƃ����ƁA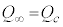 ���A
���A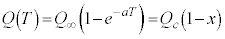 �@
�@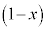 ......[�`]
......[�`]���ɁA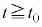 �Ƃ��āA��蕶��(iii)�����Ă݂܂��B
�Ƃ��āA��蕶��(iii)�����Ă݂܂��B
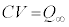 �C
�C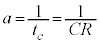 ���A�A�́A
���A�A�́A 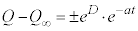 �@����D
�@����D�܂��A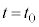 �̂Ƃ�
�̂Ƃ�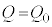 �Ƃ��āA
�Ƃ��āA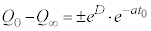 �@��
�@�� 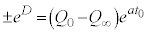 �D�ɓ��꒼���āA
�D�ɓ��꒼���āA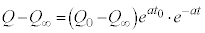 �@��
�@�� 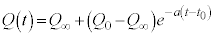 ���ꂪ��蕶��(iii)���ł��B
���ꂪ��蕶��(iii)���ł��B
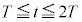 �ɂ����ẮA(iii)���ŁA
�ɂ����ẮA(iii)���ŁA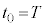 �C�܂��A�N�d�͂Ɠd���̌������t�ɂȂ�̂ŁA
�C�܂��A�N�d�͂Ɠd���̌������t�ɂȂ�̂ŁA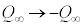 (��1���Q��)�Ƃ��āA(�`)�̌��ʂ��A
(��1���Q��)�Ƃ��āA(�`)�̌��ʂ��A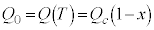 �C����āA
�C����āA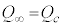 �ɒ��ӂ��āA
�ɒ��ӂ��āA 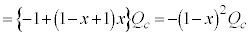 �@
�@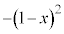 ......[��]
......[��]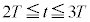 �ɂ����ẮA(iii)���ŁA
�ɂ����ẮA(iii)���ŁA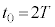 �C
�C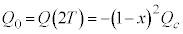 �Ƃ��āA�N�d�͂Ɠd���̌����͌��ɖ߂�̂ŁA
�Ƃ��āA�N�d�͂Ɠd���̌����͌��ɖ߂�̂ŁA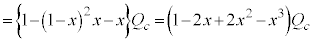 �@
�@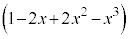 ......[�k]
......[�k]
��2�@k�����R���Ƃ��āA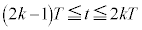 �ɂ����ẮA���̖_��Y����X�Ɍ������ĉ�]���A(iii)���ŁA
�ɂ����ẮA���̖_��Y����X�Ɍ������ĉ�]���A(iii)���ŁA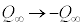 �C
�C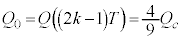 �Ƃ��A
�Ƃ��A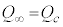 �ɒ��ӂ��āA
�ɒ��ӂ��āA 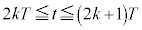 �ɂ����ẮA���̖_��X����Y�Ɍ������ĉ�]���A(iii)���ŁA
�ɂ����ẮA���̖_��X����Y�Ɍ������ĉ�]���A(iii)���ŁA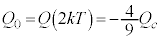 �Ƃ��A
�Ƃ��A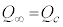 �ɒ��ӂ��āA
�ɒ��ӂ��āA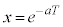 �C
�C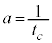 �Ȃ̂ŁA�ȏ���A
�Ȃ̂ŁA�ȏ���A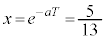 �C
�C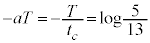
�� 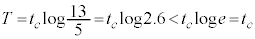 �@(��
�@(�� 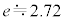 )����āA
)����āA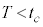
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 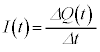 �C���̖_�ɐ�����N�d�͂�
�C���̖_�ɐ�����N�d�͂�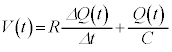 �@���(ii)
�@���(ii)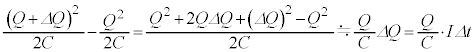 �C
�C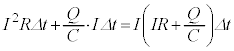 �CI�CB�CL�CT��p���ē�����̂ŁA(i)�����A
�CI�CB�CL�CT��p���ē�����̂ŁA(i)�����A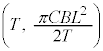 ���̒ʂ�̂ŁA�ڐ��̎��́A
���̒ʂ�̂ŁA�ڐ��̎��́A