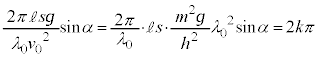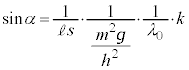���啨��'21�N�O��[3]
���̕��͂�ǂ�ŁA�@�@�@�ɓK�������܂��͐��l���A���ꂼ��̉��ɋL������B�Ȃ��A�@�@�@�͂��ł��@�@�@�ŗ^����ꂽ���̂Ɠ������̂�\���B�܂��A��1�C��2�ł́A�w���ɂ��������āA�����ꂼ��̉��ɋL������B�������A�~������π�Ƃ���B
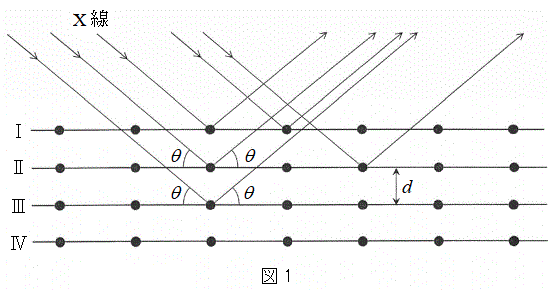
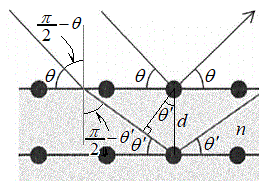
(1) �}1�̂悤�ɁAX���̌����ɂ�锽�˂��l����B�����̒��ŁA���q�͊Ԋud�ŕ��s�ɕ��ʇT�C�U�C�V�C�����ɋK������������ł���B�܂��AX���̔������͌�������\�����ꂽ�ꏊ�ɒu����Ă���AX���͌����ɑ��ē����������畽�s�ɓ��˂���Ƃ��Ă悢�B���̂Ƃ��A����X���ƌ����ʂ̂Ȃ��p�x��θ�Ƃ���B���q�ɂ�蔽�˂��ꂽX���������ʂ���p�xθ�̕����ɂ��錟�o��Ō��o����B���o�����������\�����ꂽ�ꏊ�ɂ���A���o��Ŋϑ����锽��X���͑S�ĕ��s�ł���Ƃ��Ă悢�B�����ŁAθ��0����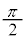 �͈̔͂ōl������̂Ƃ���B�܂�X���̔g����λ�Ƃ���B
�͈̔͂ōl������̂Ƃ���B�܂�X���̔g����λ�Ƃ���B 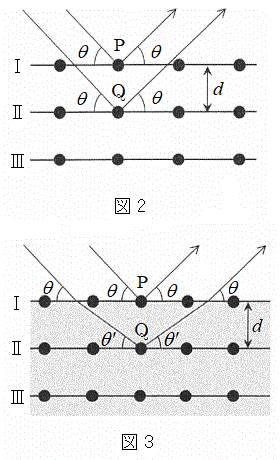 �}2�Ɏ����悤�ɁA�����ʇT��ɂ��錴�qP�ƁA���̈�w���̌����ʇU��ɂ��錴�qQ�ɂ��X���̔��˂��l����B���qQ�͌��qP�̒����ɂ�����̂Ƃ���B���̂Ƃ��A2��X���̌o�H����d�����θ��p�����@���@�ƕ\�����B�]���āA2��X�������ߍ������߂̏������́Ak�𐳂̐����Ƃ��Ĕg��λ�C�Ԋud�C����ъp�xθ��p�����@���@�ŕ\�����B
�}2�Ɏ����悤�ɁA�����ʇT��ɂ��錴�qP�ƁA���̈�w���̌����ʇU��ɂ��錴�qQ�ɂ��X���̔��˂��l����B���qQ�͌��qP�̒����ɂ�����̂Ƃ���B���̂Ƃ��A2��X���̌o�H����d�����θ��p�����@���@�ƕ\�����B�]���āA2��X�������ߍ������߂̏������́Ak�𐳂̐����Ƃ��Ĕg��λ�C�Ԋud�C����ъp�xθ��p�����@���@�ŕ\�����B
(2) ���q��X���̊Ԃɂ͂��炭�͂ɂ��AX���̋O���͌������ɓ���Ƃ킸���Ȃ���ω�����B��������ܗ��̌`�ŕ\���ƁA�������̋��ܗ�n��1��育���킸���ɏ������l�����B�܂��AX���̋�C���̋��ܗ���1�ł���Ƃ���B���ܗ����l�������(1)�ŋ��߂����������ǂ̂悤�ɕύX����邩�l�@���悤�B�}2�Ɠ��l�ɁA�����ʇT��ɂ��錴�qP�ƁA���̈�w���̌����ʇU��ɂ��錴�qQ�ɂ��X���̔��˂��l����B�������AX���͑S���˂��N����Ȃ��p�x�œ��˂�����̂Ƃ���B���̂Ƃ��A�������ł�X���̔g�����ω����A�}3�ɕ`����Ă���悤�Ɍ��qQ�ɂ͊p�xθ��菬�����p�x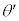 ��X�������˂��邱�ƂɂȂ邪�A
��X�������˂��邱�ƂɂȂ邪�A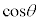 ��
��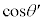 �̊Ԃɂ��@���@�Ƃ����W�������藧�B�܂��A�������̔g����
�̊Ԃɂ��@���@�Ƃ����W�������藧�B�܂��A�������̔g����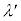 �Ƃ���ƁA
�Ƃ���ƁA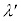 �͋�C���ł̔g��λ�ƌ������̋��ܗ�n��p�����@���@�ŕ\�����B�]���āA2��X���̈ʑ��̍��́Ad�Cλ�Cn�Cθ��p�����@���@�ƕ\�����B�������AX���̔������ɂ�����2��X���̏����ʑ��͓����ł�����̂Ƃ���B�܂��A�@���@��
�͋�C���ł̔g��λ�ƌ������̋��ܗ�n��p�����@���@�ŕ\�����B�]���āA2��X���̈ʑ��̍��́Ad�Cλ�Cn�Cθ��p�����@���@�ƕ\�����B�������AX���̔������ɂ�����2��X���̏����ʑ��͓����ł�����̂Ƃ���B�܂��A�@���@��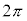 �̐����{�̏ꍇ�ɂ�X�������ߍ����Ƃ�����������A2��X�������ߍ������߂̏������́Ad�Cλ�Cn�Cθ�C���̐���k��p�����@���@�ŕ\�����B
�̐����{�̏ꍇ�ɂ�X�������ߍ����Ƃ�����������A2��X�������ߍ������߂̏������́Ad�Cλ�Cn�Cθ�C���̐���k��p�����@���@�ŕ\�����B
 (3) �d�q�⒆���q�Ȃǂ̗��q�́A�g���̐������������Ƃ��m���Ă���B������h�E�u���C�g(�����g)�Ƃ����A���̔g��λ�͗��q�̎��ʂ�m�C������v�Ƃ���
(3) �d�q�⒆���q�Ȃǂ̗��q�́A�g���̐������������Ƃ��m���Ă���B������h�E�u���C�g(�����g)�Ƃ����A���̔g��λ�͗��q�̎��ʂ�m�C������v�Ƃ���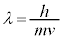
�ŗ^������B�����ŁAh�̓v�����N�萔�ƌĂ��萔�ł���B�h�E�u���C�g�͎���T�C�g��λ�̐����g�ŕ\���A���q�������ɓ��˂����X���̂Ƃ��̂悤�ɉ�܂⊱���N����B
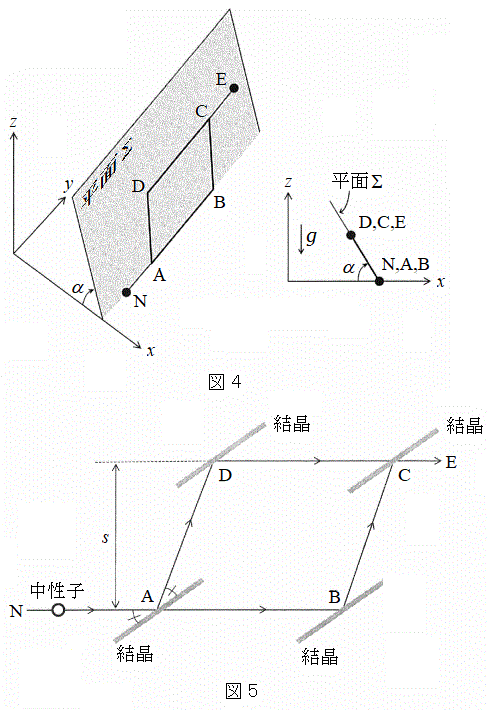
���܁A�}4�Ɏ����悤��xy���ʂ������ʁAz�����������d�͂̌����ƂȂ�悤�������W�����Ƃ�A�d�͉����x�̑傫����g�Ƃ���B����Σ�́A�����ʂƌ���钼����y���ƕ��s�ƂȂ镽�ʂł���A���̒��������ɂ��ĉ�]�ł�����̂Ƃ���B����Σ�������ʂƂȂ��p��α�Ƃ���(�}4�̊p�x�̌����𐳂Ƃ���)�B����Σ���ɕ��s�l�ӌ`ABCD�C�����ē_E�CN�����݂��A��AB�͐����ʏ�ɂ���B�_N�CA�CB����ѓ_D�CC�CE�́A���ꂼ�ꓯ��������ɂ���A��AB�ƕ�DC�̊Ԋu��s�ł���(�}5�Q��)�B
����Σ���̏ڍׂ�}5�Ɏ����B�����ŁA�����q�����s�l�ӌ`ABCD��̕ӂ��^������悤�A�K���Ȍ�����_A�CB�CC�CD�ɓK�Ȋp�x�Ŕz�u���A�_N�ɂ��钆���q������_A�ɑ���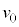 ���������q�̃r�[������˂�����B�������A�����q�͏\���ɑ����A�����q�̋O���͏d�͂ɂ���ĉe�����Ȃ��Ƃ���B�܂��A�����̌����͖����ł���قǏ\�������Ƃ��A����ɁA�������̋��ܗ��͋ߎ��I��
���������q�̃r�[������˂�����B�������A�����q�͏\���ɑ����A�����q�̋O���͏d�͂ɂ���ĉe�����Ȃ��Ƃ���B�܂��A�����̌����͖����ł���قǏ\�������Ƃ��A����ɁA�������̋��ܗ��͋ߎ��I��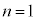 �Ƃ��Ď�舵�����̂Ƃ���B�����q�̎��ʂ�m�Ƃ��A���˂���h�E�u���C�g�̔g����
�Ƃ��Ď�舵�����̂Ƃ���B�����q�̎��ʂ�m�Ƃ��A���˂���h�E�u���C�g�̔g����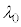 �Ƃ���B���̒����q�r�[���͈�ʂɌ����߂��鐬���ƌ����ɂ��U������鐬���ɕ�����邪�A�U������鐬���ɑ��Ă�(1)�ŋ��߂����˂̏����������������̂Ƃ���B������2�ɕ����ꂽ�����q�̔g���ēx2�̌�����̓_B�����D�Ŕ��˂����邱�Ƃɂ��A�_C�ɏW���A�_E�Ńh�E�u���C�g���ϑ�����B
�Ƃ���B���̒����q�r�[���͈�ʂɌ����߂��鐬���ƌ����ɂ��U������鐬���ɕ�����邪�A�U������鐬���ɑ��Ă�(1)�ŋ��߂����˂̏����������������̂Ƃ���B������2�ɕ����ꂽ�����q�̔g���ēx2�̌�����̓_B�����D�Ŕ��˂����邱�Ƃɂ��A�_C�ɏW���A�_E�Ńh�E�u���C�g���ϑ�����B
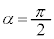 �ɂƂ�A���s�l�ӌ`ABCD�������ʂɑ��Đ����ɂȂ�ꍇ���l����B�����q����DC���Ƃ��́A������
�ɂƂ�A���s�l�ӌ`ABCD�������ʂɑ��Đ����ɂȂ�ꍇ���l����B�����q����DC���Ƃ��́A������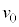 �ƈقȂ邽�߁A
�ƈقȂ邽�߁A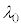 �C
�C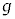 �C
�C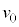 �Cs��p����ƁA�g�����@���@�ƂȂ�B�@���@��
�Cs��p����ƁA�g�����@���@�ƂȂ�B�@���@��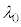 �̈Ⴂ�͔��ɏ��������A2�̈قȂ�o�H�ɂ��h�E�u���C�g�̊������邱�Ƃɂ��A�����q�ɑ���d�͂̉e�����ϑ����邱�Ƃ��ł���B
�̈Ⴂ�͔��ɏ��������A2�̈قȂ�o�H�ɂ��h�E�u���C�g�̊������邱�Ƃɂ��A�����q�ɑ���d�͂̉e�����ϑ����邱�Ƃ��ł���B
��1�@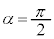 �ɂƂ�A��AB�̒�����
�ɂƂ�A��AB�̒�����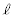 �Ƃ����Ƃ��A�����q���o�HABCE��ʂ�ꍇ�ƌo�HADCE��ʂ�ꍇ�ŁA�����g�̈ʑ��̍������߁A
�Ƃ����Ƃ��A�����q���o�HABCE��ʂ�ꍇ�ƌo�HADCE��ʂ�ꍇ�ŁA�����g�̈ʑ��̍������߁A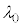 �Cm�C
�Cm�C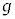 �Cs�C
�Cs�C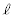 �Ch�C
�Ch�C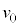 �̒�����K�v�Ȃ��̂�p���ē�����B���o�ߒ��������B�Ȃ��A�h�E�u���C�g�̎���T��2�̌o�H�ŕω������A�ʑ��̍��͔g���̈Ⴂ�݂̂Ō��܂�B����ɁA
�̒�����K�v�Ȃ��̂�p���ē�����B���o�ߒ��������B�Ȃ��A�h�E�u���C�g�̎���T��2�̌o�H�ŕω������A�ʑ��̍��͔g���̈Ⴂ�݂̂Ō��܂�B����ɁA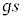 ��
��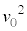 �ɔ�ׂĂ͂邩�ɏ��������̂Ƃ��A�K�v�ɉ�����
�ɔ�ׂĂ͂邩�ɏ��������̂Ƃ��A�K�v�ɉ�����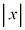 ��1���\���ɏ������Ƃ��ɐ��藧�ߎ���
��1���\���ɏ������Ƃ��ɐ��藧�ߎ��� ��p���Ă��悢�B
��2�@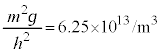 �C
�C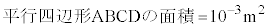 �C���˂���h�E�u���C�g�̔g��
�C���˂���h�E�u���C�g�̔g��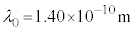 �Ƃ���B�ȉ��̖₢�ɓ�����B
�Ƃ���B�ȉ��̖₢�ɓ�����B (i) �}4�̊p�xα��ω������Ȃ���_E�Œ����q�r�[�����x���ϑ����邱�Ƃɂ��A�d�͂̉e�����݂邱�Ƃ��ł���B�p�xα��0����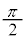 �܂ő����������Ƃ��A�_E�Œ����q�r�[�������ɂ�苭�ߍ������Ƃ�����N���邩������B
�܂ő����������Ƃ��A�_E�Œ����q�r�[�������ɂ�苭�ߍ������Ƃ�����N���邩������B (ii) �p�xα��0���瑝���������Ƃ��A�_E�Œ����q�r�[�����͂��߂Ċ��ɂ���ߍ����Ƃ���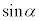 �̒l��L������2�����œ�����B
�̒l��L������2�����œ�����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�O���͊�b�I���ł����A�㔼�́A�Ȃ����s�l�ӌ`�Ȃ낤�A�Ȃǂƍl���Ă��܂��ƍ������邩���m��܂���B�@
(1) 2��X���̌o�H���́A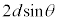 ......[��]
......[��]
2��X�������ߍ������߂̏������́A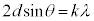 ......[��]�@(�g�̊������Q��)
......[��]�@(�g�̊������Q��)
 (2) ���ˊp��
(2) ���ˊp�� �C���܊p��
�C���܊p��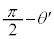 �ł��B���܂̖@�����A
�ł��B���܂̖@�����A
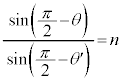 �@��
�@�� 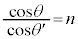 ......[��]
......[��]���ܗ�n�̕������ł́A���̔g����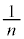 �ɂȂ�̂ŁA
�ɂȂ�̂ŁA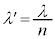 ......[��]
......[��]
2��X�����ʑ����́Ad�Cλ�Cn�Cθ��p���ē�����̂ŁA(��)�A(��)�̌��ʂ�p���āA 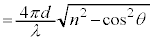 ......[��]
......[��]2��X�������ߍ������߂̏�������(�g�̊������Q��)�A�ʑ�����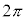 �̎��R���{�ƂȂ邱�ƂŁA
�̎��R���{�ƂȂ邱�ƂŁA 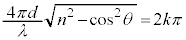 �@��
�@�� 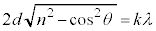 ......[��]
......[��]
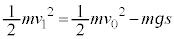 �@��
�@�� 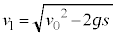 �@����A
�@����A��DC�Ԃ������q�̃h�E�u���C�g��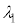 �́A
�́A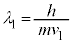
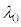 �C
�C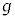 �C
�C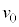 �Cs��p���ē�����̂ŁA�@�C�A���A
�Cs��p���ē�����̂ŁA�@�C�A���A 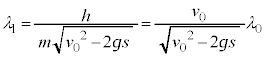 ......[��]
......[��]
��1�@2�o�H�ŁAA��D��B��C�ƂŒ����q�̈ړ����ԂɈႢ�͂Ȃ��AA��B��D��C�ł͑����̈Ⴂ�ɂ���Ĕg�����قȂ�A2�o�H�ł̃h�E�u���C�g���ʑ����́A(��)�̌��ʂ�p���āA����ɖ�蕶�̋ߎ����s���ƁA 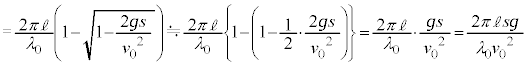 ......[��]�@(
......[��]�@( ���g��Ȃ�������������܂�)
���g��Ȃ�������������܂�)
��2�@�p�xα��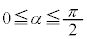 �͈̔͂ŕω�����ƁA��DC��xy���ʂ���̍�����s����
�͈̔͂ŕω�����ƁA��DC��xy���ʂ���̍�����s����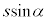 �ւƕω����܂��B���̂Ƃ��̕�DC�Ԃ������q�̑���
�ւƕω����܂��B���̂Ƃ��̕�DC�Ԃ������q�̑���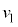 �A�܂��h�E�u���C�g��
�A�܂��h�E�u���C�g��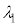 �́A�A��[��]�̌��ʂ�
�́A�A��[��]�̌��ʂ�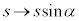 �Ƃ��āA
�Ƃ��āA 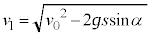 �C
�C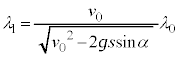
��1�̌��ʂ��A2�o�H�ł̃h�E�u���C�g�̈ʑ����́A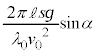 �ƂȂ�܂����A�@���A
�ƂȂ�܂����A�@���A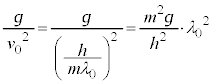 �ƂȂ�̂ŁA2�o�H�ł̃h�E�u���C�g�����߂�������(�g�̊������Q��)�́Ak�𐮐��Ƃ��āA
�ƂȂ�̂ŁA2�o�H�ł̃h�E�u���C�g�����߂�������(�g�̊������Q��)�́Ak�𐮐��Ƃ��āA �^����ꂽ���l��������(���s�l�ӌ`�̖ʐς�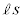 �ł�)�A
�ł�)�A 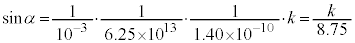 �@����B
�@����B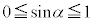 ���A
���A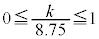 �C
�C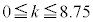
�����������k�́A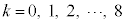 ��9�B����āA�����q�r�[�������ɂ�苭�ߍ������Ƃ�9�� ......[��] �N����܂��B
��9�B����āA�����q�r�[�������ɂ�苭�ߍ������Ƃ�9�� ......[��] �N����܂��B
�p�xα��0���瑝���������Ƃ��A�_E�Œ����q�r�[�����͂��߂Ċ��ɂ���ߍ����̂́A�B��k���A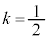 �̂Ƃ�(��߂����Ƃ��Ȃ̂ŁAk�͔������ł�)�ŁA
�̂Ƃ�(��߂����Ƃ��Ȃ̂ŁAk�͔������ł�)�ŁA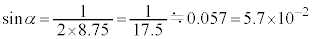 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 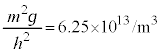 �C
�C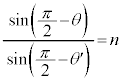 �@��
�@�� 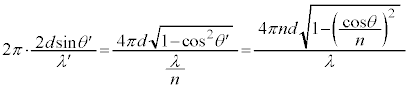
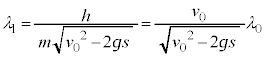 ......[��]
......[��]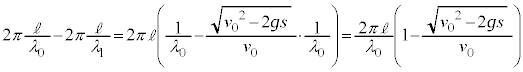
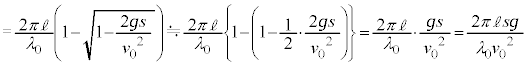 ......[��]�@(
......[��]�@(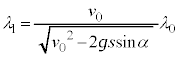
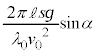 �ƂȂ�܂����A�@���A
�ƂȂ�܂����A�@���A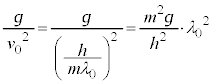 �ƂȂ�̂ŁA2�o�H�ł̃h�E�u���C�g�����߂�������(�g�̊������Q��)�́Ak�𐮐��Ƃ��āA
�ƂȂ�̂ŁA2�o�H�ł̃h�E�u���C�g�����߂�������(�g�̊������Q��)�́Ak�𐮐��Ƃ��āA