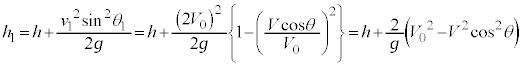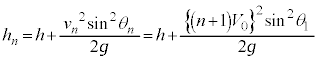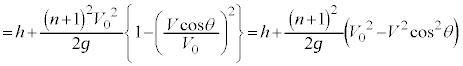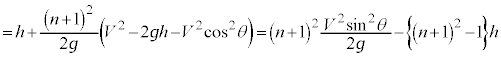���啨�� '21 �N�O�� [1] ���̕��͂�ǂ�ŁA 1 �ł́A�w���ɂ��������āA�����ꂼ��̉��ɋL������B�������A�d�͉����x�̑傫���� (1) �} 1(a) �̂悤�ɁA���� m �̏������A�����x�̑傫�� V �C�n�\���������Ɋp�x θ �œ����グ��B�����͍ő卂�x A �̍��x h �ɂ����āA���� M �̃{�[���ƈꎟ���I�ɏՓ˂����A���̔����𗘗p���ď������������ˏグ��B�����ŁA�ꎟ���I�ɏՓ˂���Ƃ́A�} 1(b) �̂悤�ɏՓ˒��O����̏����ƃ{�[�������꒼����ɉ����ĉ^�����邱�Ƃ������A���̒����ɉ����Փˎ����`����B�Փˎ��͏Փ˒��O�̃{�[���̐i�s�����𐳂Ƃ��A�Փˎ������̑��x�������A�ȉ������āu���x�����v�ƋL�ڂ���B�Ȃ��A�Փ˂͏u�ԓI�ɋN������̂Ƃ��A�����ƃ{�[���̑傫���A����ы�C��R�̉e���͖�������B �} 1(b) �̂悤�ɁA�Փ˒��O�̏����ɂ��āA���̑��x�̑傫���� V �C θ �C h �C �@��� (i) �����ŁA m �C M �C����� �@��� (ii) �����藧�̂ŁA�� (i) �C (ii) ���A�Փ˒���̑��x���� m �C M ��p���� M �������̎��� m �� 0 �ƂȂ�A�Փ˒���̏����̑��x���� h �C V �C θ �C (2) (1) �̏���������ɍ������ˏグ�邽�߁A�} 2 �̂悤�ɁA�ő卂�x�ɓ��B������ɗ������Ă��鏬���߂����āA���x h �Ń{�[�����Փ˂�����A�Ƃ����ߒ����J��Ԃ��s�Ȃ����Ƃ��悤�B�����ŁA (1) �Ɠ��l�ɁA�����ƃ{�[���͈ꎟ���I�ɏՓ˂��A�} 3 �̂悤�ɏՓ˂��Ƃɒ�`�����Փˎ������̑��x�������A�ȉ������āu���x�����v�ƋL�ڂ���B�܂� n ��� ( �̏Փˎ��̃{�[���́A�Փ˒��O�̑��x�̑傫���� 0 �ƂȂ鎿�� ���̂Ƃ��A n ��ڂ̏Փ˒���ɂ����鏬���̑��x���� �@��� (iii) (1) ���A (iii) �������āA h �C V �C θ �C n ��p���āA �� 1 �@ (2) �ɂ�����Փˉߒ��ɂ��āA�ȉ��̖₢�ɓ�����B
(i) n ��ڂɏՓ˂�����{�[���̎��� m �̉��{�ɂ���悢���B n ��p���ĕ\���B���o�ߒ��������B (ii) �Փ˂�����{�[���̎��ʂɏ��������ƁA�Փ˒���̃{�[���̑��x������ 0 �ƂȂ�Փˉɏ�����ł���B�{�[���̎��ʂ̏���������̎��� m �� 10 �{�ł���ꍇ�A�Փˉ�����ɒB�����Ƃ��̏��������B����ő卂�x�́A�{�[���ƏՓ˂���O�̍ő卂�x �y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�� �@�����ɂ��ʓ|�Ȍv�Z�ɂȂ肻���ȌJ��Ԃ� �Փ� �̖��ł����A�U���ʂ�i�߂Ă����Α債�����Ƃ͂���܂���B �@�� �A ] �@����@ �Փ˂܂ł̏����̉^���́A���������͑��� �@����A ......[ �C ] ......[ �E ] �@����B �����W���̎� �F ......[ �G ] �@�� �@����C �B�ɑ�����āA �I ] �C�ɑ�����āA ......[ �J ] �Ƃ���ƁA 3 ......[ �L ] �I ] �̌��ʂɑ�����āA 2 ......[ �N ] ���������ɂ��āA�Փ˒���ɏ����x 0 �C�ō��_�܂ł� �������x�^�� �̌������A �@�C�A�C ( �N ) �̌��ʂ�p���āA
......[ �P ] �@�� �R ] [ �N ] �̌��ʂ�� 1 �� �������� �ŁA ......[ �T ] ��ڂ̏Փ˒���̏����̑��x������ �͊w�I�G�l���M�[�ۑ� ���A n ��ڂ̏Փ˒��O�̏����̑����� n ��ڂ̏Փˎ��Ɛ��������Ƃ̂Ȃ��p�� �C�]���āA n ��ڂ̏Փ˒���ɏ����x 0 �C�ō��_�܂ł� �������x�^�� �̌������A [ �T ] �̌��ʂ��A
�� 1(i) [ �T ] �̌��ʂ��A (ii) ���A n �̏���� �ŏ��ɓ����グ���Ƃ��̏����x�̉������������� �������x�^�� �̌������A �@�� [ �V ] �̌��ʂŁA �C 25 �{ ......[ �� ] �y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@ ���啨�� TOP �@�@ ���� TOP �@�@ TOP �y�[�W�ɖ߂� �y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B �e���̒��쌠�� © 2005-2024 (�L)����� ��w�y�w�m ���������t���I ���n��w�l�b�g�m ��w�y�w�m (���ē��������� )������́A������܂Ń��[�� �� 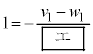 �@���(ii)
�@���(ii)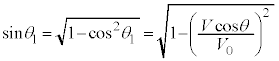 �@����A
�@����A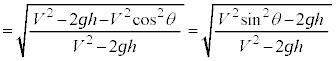 ......[�C]
......[�C]