���s��w2023�N�O�������������
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
[1]�@���̕��͂�ǂ�ŁA�@�@�ɓK�������܂��͐��l���A���ꂼ��̉��ɋL������B�Ȃ��A�@�@�͂��ł��@�@�ŗ^����ꂽ���̂Ɠ������̂�\���B�܂��A��1�C��2�ł́A�w���ɂ��������āA�����ꂼ��̉��ɋL������B�������A�~������π�Ƃ���B
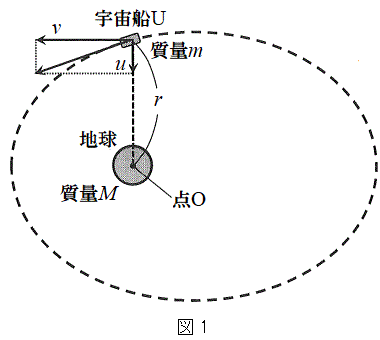 (1) �}1�̂悤�ɓ_O�𒆐S�Ƃ��鎿��M�̒n���̂܂����A�n�����\������������m�̉F���DU���ȉ~�O���ł܂���Ă���B�F���DU����_O�Ɍ����������̑�����u�C����Ɛ����ȕ����̑�����v�C�F���DU�Ɠ_O�Ԃ̋�����r�Ƃ��A�F���DU�ɂ͓_O�Ɍ����������̖��L���݂͂̂��͂��炭���̂Ƃ���B���̂Ƃ��A�F���DU�̉^���G�l���M�[��m�Cu�Cv�ŕ\�����@�A�@�ł���A����ɁA�ʒu�G�l���M�[�͖���������0�Ƃ��Ė��L���͒萔G�����M�Cm�Cr�ŕ\�����@�C�@�ł���B�F���DU�̗͊w�I�G�l���M�[�̈��lE�Ƃ����
(1) �}1�̂悤�ɓ_O�𒆐S�Ƃ��鎿��M�̒n���̂܂����A�n�����\������������m�̉F���DU���ȉ~�O���ł܂���Ă���B�F���DU����_O�Ɍ����������̑�����u�C����Ɛ����ȕ����̑�����v�C�F���DU�Ɠ_O�Ԃ̋�����r�Ƃ��A�F���DU�ɂ͓_O�Ɍ����������̖��L���݂͂̂��͂��炭���̂Ƃ���B���̂Ƃ��A�F���DU�̉^���G�l���M�[��m�Cu�Cv�ŕ\�����@�A�@�ł���A����ɁA�ʒu�G�l���M�[�͖���������0�Ƃ��Ė��L���͒萔G�����M�Cm�Cr�ŕ\�����@�C�@�ł���B�F���DU�̗͊w�I�G�l���M�[�̈��lE�Ƃ�����ƕ\�����Ƃ��ł���B�����ŁA�P�v���[�̑�2�@��(�ʐϑ��x���̖@��)�����藧���Ƃ���ʐϑ��x�����̒l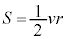 �Ƃ��āAr���܂ލ����܂Ƃ߂���
�Ƃ��āAr���܂ލ����܂Ƃ߂���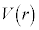 ��G�CM�Cm�Cr�CS��p���ĕ\�����@�E�@�ł���B�F���DU���ȉ~�O�����^������ԁA
��G�CM�Cm�Cr�CS��p���ĕ\�����@�E�@�ł���B�F���DU���ȉ~�O�����^������ԁA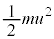 ��0���ŏ��l�Ƃ���L���͈̔͂�ω�����B���������āA
��0���ŏ��l�Ƃ���L���͈̔͂�ω�����B���������āA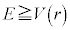 �ƂȂ�r�͈̔͂��A�F���DU�Ɠ_O�Ԃ̋������ω�����͈͂�\���B
�ƂȂ�r�͈̔͂��A�F���DU�Ɠ_O�Ԃ̋������ω�����͈͂�\���B
��1�@��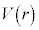 �̊T�`�͂ǂ̂悤�ɂȂ邩�Br�������C
�̊T�`�͂ǂ̂悤�ɂȂ邩�Br�������C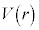 ���c���Ƃ��ē���
���c���Ƃ��ē���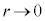 ��
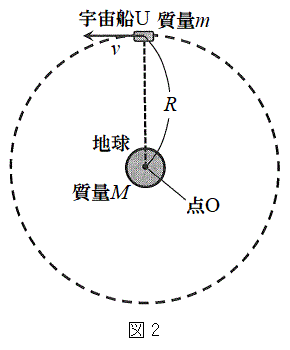
��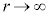 �̂Ƃ��̐U�镑�����킩��悤�ɃO���t�ɕ`���B���̂Ƃ��A�n����傫���������ł��鎿��M�̎��_�Ƃ݂Ȃ��B�܂��A�����A�c����0�ȊO�̒l���L������K�v�͂Ȃ��B
�̂Ƃ��̐U�镑�����킩��悤�ɃO���t�ɕ`���B���̂Ƃ��A�n����傫���������ł��鎿��M�̎��_�Ƃ݂Ȃ��B�܂��A�����A�c����0�ȊO�̒l���L������K�v�͂Ȃ��B
 (2) �}2�̂悤�ɁA�F���DU�̋O�������aR�̉~�O���Ƃ݂Ȃ���ꍇ���l����B����R�͈ȉ��ŏ�Ɉ��l���Ƃ�A���������āA(1)��r�ƈقȂ邱�Ƃɒ��ӂ���B���̂Ƃ��A�F���DU�̑�����v�C�O����������������T�Ƃ���B����T��G�CM�CR�ŕ\�����@�G�@�ł���B
(2) �}2�̂悤�ɁA�F���DU�̋O�������aR�̉~�O���Ƃ݂Ȃ���ꍇ���l����B����R�͈ȉ��ŏ�Ɉ��l���Ƃ�A���������āA(1)��r�ƈقȂ邱�Ƃɒ��ӂ���B���̂Ƃ��A�F���DU�̑�����v�C�O����������������T�Ƃ���B����T��G�CM�CR�ŕ\�����@�G�@�ł���B���ɁA�F���DU�ɁA�_O�Ɍ���������(���a����)�ɏ\���ア�͂��O������u�ԓI�ɉ�������ꍇ���l����B����ƁA�F���DU�͌��̉~�O���Ƃ͂킸���ɈقȂ�O�������ǂ�n�߂�B���̌�̉^�����ȉ��̂悤�ɍl�@���悤�B�F���DU�̔��a�����̈ʒu���������𐳂Ƃ���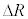 ���������ɂ��ꂽ�_�A���Ȃ킿�_O���狗��
���������ɂ��ꂽ�_�A���Ȃ킿�_O���狗��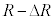 �̓_�ł́A���a�����ɐ����ȕ����̑�����
�̓_�ł́A���a�����ɐ����ȕ����̑�����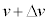 �Ƃ��A
�Ƃ��A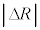 ��
��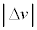 �͂��ꂼ��R��v�ɔ��ɏ\���������Ƃ���B�u�ԓI�ȊO�͂ɂ��F���DU�̉^���G�l���M�[�͂킸���ɑ������邪�A���a�����̗͂ł��邽�߃P�v���[�̑�2�@���͂��̊ԁA��ɐ�������B������A
�͂��ꂼ��R��v�ɔ��ɏ\���������Ƃ���B�u�ԓI�ȊO�͂ɂ��F���DU�̉^���G�l���M�[�͂킸���ɑ������邪�A���a�����̗͂ł��邽�߃P�v���[�̑�2�@���͂��̊ԁA��ɐ�������B������A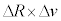 �ɔ�Ⴗ�鍀������ƁAR�C
�ɔ�Ⴗ�鍀������ƁAR�C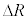 �Cv��p����
�Cv��p����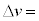 �@�I�@�ƕ\����B
�@�I�@�ƕ\����B
�ʒu�����̉~�O���̔��aR����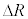 ���������ɂ��ꂽ���ƂŁA�F���DU�ɂ͂��炭�͂��ǂ̂悤�ɕω����邩���߂悤�B�ȉ��ł́A
���������ɂ��ꂽ���ƂŁA�F���DU�ɂ͂��炭�͂��ǂ̂悤�ɕω����邩���߂悤�B�ȉ��ł́A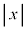 �C
�C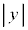 ��1���\���������Ƃ��ɐ��藧�ߎ���
��1���\���������Ƃ��ɐ��藧�ߎ��� �C
�C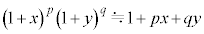 (p�Cq�͎���)��p����B�܂��A���L���͂̑傫���̑�����
(p�Cq�͎���)��p����B�܂��A���L���͂̑傫���̑�����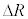 �ɔ�Ⴗ��`��G�CM�Cm�CR��p���ĕ\����
�ɔ�Ⴗ��`��G�CM�Cm�CR��p���ĕ\���� 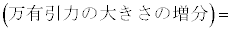 �@�J�@
�@�J�@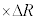
�ł���B����A���S�͔͂��a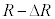 �C����
�C����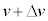 �̉~�^���Ɠ��l�ɍl���邱�Ƃ��ł���B������A���S�͂̑傫���̑�����
�̉~�^���Ɠ��l�ɍl���邱�Ƃ��ł���B������A���S�͂̑傫���̑�����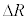 �ɔ�Ⴗ��`��m�CR�Cv��p���ĕ\����
�ɔ�Ⴗ��`��m�CR�Cv��p���ĕ\���� 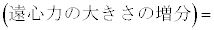 �@�L�@
�@�L�@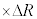
�ł���B�ȏ���A�������𐳂Ƃ��鍇�͂̑�����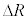 �ɔ�Ⴗ��`��G�CM�Cm�CR��p����
�ɔ�Ⴗ��`��G�CM�Cm�CR��p���� 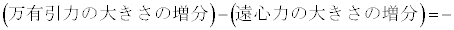 �@�N�@
�@�N�@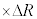
�Ƌ��܂�B���������āA���̗͉͂F���DU�̔��a�����̈ʒu�̂�������ɖ߂������͂Ƃ��Ă͂��炭�B���̗͂������N���������x��������𐳂Ƃ���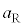 �ƒ�`����ƁA���a�����̉^����������
�ƒ�`����ƁA���a�����̉^����������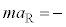 �@�N�@
�@�N�@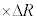 �ƂȂ�B�ȏ�̋c�_��
�ƂȂ�B�ȏ�̋c�_��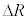 �����A�܂�F���DU�̈ʒu�����aR����O���ɂ��ꂽ�ꍇ�ɂ���������B����āA��L�̉^������������F���DU�͔��a�����̔����ψ�
�����A�܂�F���DU�̈ʒu�����aR����O���ɂ��ꂽ�ꍇ�ɂ���������B����āA��L�̉^������������F���DU�͔��a�����̔����ψ�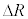 �ɂ��ĒP�U�����邱�Ƃ��킩��B���̔����ȐU���^���̎�����t �Ƃ���ƁA�F���DU���O��������������T�Ƃ̔�
�ɂ��ĒP�U�����邱�Ƃ��킩��B���̔����ȐU���^���̎�����t �Ƃ���ƁA�F���DU���O��������������T�Ƃ̔�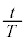 ���@�P�@�ł���B���̉^���͌��̉~�^���Ƃ͈قȂ���̂́A�F���DU�����̌���p�����Ēn�����������邱�Ƃ͕ς��Ȃ��B
���@�P�@�ł���B���̉^���͌��̉~�^���Ƃ͈قȂ���̂́A�F���DU�����̌���p�����Ēn�����������邱�Ƃ͕ς��Ȃ��B
(3) ����m�̉F���DU������M�̓V��X�̂܂����^������ꍇ���l����Bm��M���\���������Ƃ���B�F���DU�ɂ͓V��X����̈��݂͂̂��͂��炭���A���̗͂̑傫���̓j���[�g���̖��L���̖͂@�����܂ވ�ʓI�Ȍ`�ŁA
�ƕ\����Ƃ���B�����ŁAr�͓V��X�̒��S����F���DU�܂ł̋����AA��k�͐��̒萔�ł���A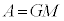 �C
�C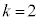 �Ȃ�j���[�g���̖��L���̖͂@���ɑ�������B�Ȃ��ȉ��ł́A�V��X����̈��͈ȊO�̕����@���A���Ȃ킿���S�͂�\�����ƃP�v���[�̑�2�@���͕ς�炸���藧���̂Ƃ���B
�Ȃ�j���[�g���̖��L���̖͂@���ɑ�������B�Ȃ��ȉ��ł́A�V��X����̈��͈ȊO�̕����@���A���Ȃ킿���S�͂�\�����ƃP�v���[�̑�2�@���͕ς�炸���藧���̂Ƃ���B
���܁A�C�ӂ�k�̏ꍇ�ɑ��āA���̈��͂����S�͂Ƃ���A�V��X�̒��S�����锼�aR�̉~�^�����l���邱�Ƃ��ł���B���̂Ƃ��̔��a�����ɐ����ȕ����̑�����A�CR�Ck�ŕ\�����@�R�@�ł���B�����ŁA�F���DU�ɁA�V��X�̒��S�Ɍ����������ɏ\���ア�͂��O������u�ԓI�ɉ�������ꍇ���l�@���悤�B(2)�Ɠ��l�ɁA�F���DU�̋O�����킸���ɓ������ɕω������Ƃ���D�F���DU�̋O���̂��ꂪ�������𐳂Ƃ���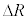 �̏ꍇ�A���͂̑�����(2)�Ɠ��l�̕��@�ōl���邱�Ƃ��ł���B���͂̑傫����\������
�̏ꍇ�A���͂̑�����(2)�Ɠ��l�̕��@�ōl���邱�Ƃ��ł���B���͂̑傫����\������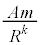 �ƂȂ������Ƃɒ��ӂ��A���̑�����
�ƂȂ������Ƃɒ��ӂ��A���̑�����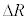 �ɔ�Ⴗ��`��A�Cm�CR�Ck��p���ĕ\����
�ɔ�Ⴗ��`��A�Cm�CR�Ck��p���ĕ\���� 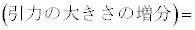 �@�T�@
�@�T�@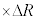
�ł���B�������𐳂Ƃ��鍇�͂̑�����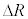 �ɔ�Ⴗ��`��A�Cm�CR�Ck��p����
�ɔ�Ⴗ��`��A�Cm�CR�Ck��p���� 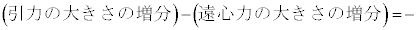 �@�V�@
�@�V�@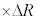
�Ƌ��܂�B�ȏ�̋c�_��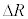 �����A�܂�F���DU�̈ʒu�����aR����O���ɂ��ꂽ�ꍇ�ɂ���������B
�����A�܂�F���DU�̈ʒu�����aR����O���ɂ��ꂽ�ꍇ�ɂ���������B
������A�F���DU�̉^����k�̒l�ɉ����ĈقȂ邱�Ƃ��ȉ��̂悤�ɂ킩��B�܂��A(2)�ōl�����悤�Ȕ��a�����̔����U�����^���ƂȂ�̂�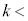 �@�X�@�̏ꍇ�݂̂ł���B�܂��A���̏ꍇ�A�����ȐU���̎���
�@�X�@�̏ꍇ�݂̂ł���B�܂��A���̏ꍇ�A�����ȐU���̎���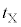 �ƋO��������������
�ƋO��������������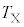 �̔�
�̔�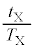 ��k�݂̂̊��Ƃ����@�Z�@�ƕ\����B
��k�݂̂̊��Ƃ����@�Z�@�ƕ\����B
��2�@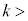 �@�X�@�̏ꍇ�A�O����������
�@�X�@�̏ꍇ�A�O����������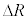 �������ꂽ�Ƃ��ɍ��͂̑����̂͂��炭�����͂ǂ�������ŁA�傫����
�������ꂽ�Ƃ��ɍ��͂̑����̂͂��炭�����͂ǂ�������ŁA�傫����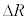 �ƂƂ��ɂǂ̂悤�ɕς�邩�A
�ƂƂ��ɂǂ̂悤�ɕς�邩�A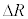 �����̏ꍇ�ɂ��ē�����B�܂��A���̌��ʁA�F���DU�̉^���͂ǂ̂悤�ɂȂ邩�q�ׂ�B
�����̏ꍇ�ɂ��ē�����B�܂��A���̌��ʁA�F���DU�̉^���͂ǂ̂悤�ɂȂ邩�q�ׂ�B
[��]
[2]�@���̕��͂�ǂ�ŁA�@�@�ɓK�������܂��͐��l���A{�@�@}����͓K�Ȃ��̂���I�т��̔ԍ����A���ꂼ��̉��ɋL������B�Ȃ��A�@�@�͂��ł��@�@�ŗ^����ꂽ���̂Ɠ������̂�\���B�܂��A��1�C��2�ł́A�w���ɂ��������āA�����ꂼ��̉��ɋL������B�������A�^�̃N�[�����̖@���̔��萔��k�C�~������π�Ƃ���B
(1) �^�ɒu���ꂽ���̓d�C��Q�̓_�d�ׂ���o��d�C�͐��̖{�����l����B�_�d�ׂ𒆐S�Ƃ��鋅�ʂ��l����ƁA���̋��ʂ��т��P�ʖʐς�����̓d�C�͐��̖{��(�d�C�͐��̖��x)�́A�d��̋����Ɠ������Ȃ�悤�ɒ�߂��Ă���B���̂��Ƃ���A�_�d�ׂ���o��d�C�͐��̖{�����@�C�@�ł���B
(2) �^�ɂ��锼�aa�̓��̋�A�ɐ��̓d�C��Q��^����ƁA�d�ׂ�{���F�@�����S�̂ɁC�A���̕\�ʂ�}��l�ɕ��z����B���̒��SO���狗��r�̋��ʂ��т��d�C�͐��̖{����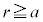 �ł��@�C�@�ŁA�d�C��Q�̓_�d�ׂ𒆐SO�ɒu�����Ƃ��Ɠ����ł���B���̂��߁A�d��̋����Ɠd�ʂ́A�_�d�ׂ̏ꍇ�ƕς��Ȃ��B����A
�ł��@�C�@�ŁA�d�C��Q�̓_�d�ׂ𒆐SO�ɒu�����Ƃ��Ɠ����ł���B���̂��߁A�d��̋����Ɠd�ʂ́A�_�d�ׂ̏ꍇ�ƕς��Ȃ��B����A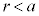 �ł͓d��̋������@�n�@�ŁA�d�ʂ��@�j�@�ƂȂ�B�������A��������d�ʂ̊(�d�ʁ�0)�Ƃ���B
�ł͓d��̋������@�n�@�ŁA�d�ʂ��@�j�@�ƂȂ�B�������A��������d�ʂ̊(�d�ʁ�0)�Ƃ���B
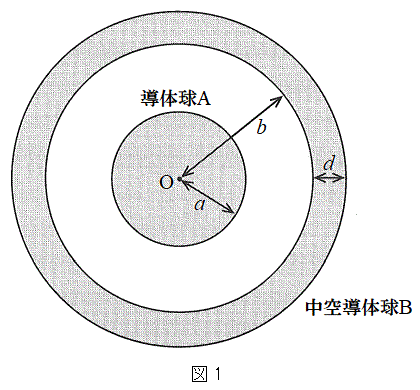 (3) (2)�̏�Ԃɂ��铱�̋�A���A�}1�̒f�ʐ}�̂悤�ɁA�d�ׂ��^�����Ă��Ȃ�����̓��̋�B(�����ab�C����d)�ň͂ށB�������A���̋�A�ƒ��̋�B�͓���̓_O�𒆐S�Ƃ���B���̋�B���A���̋�A������d��̒��ɒu�����̂ŁA���̋�B�ɂ͐Ód�U���ɂ���Đ��d�ׂƕ��d�ׂ̕��z�̕肪�������B���̌��ʁA
(3) (2)�̏�Ԃɂ��铱�̋�A���A�}1�̒f�ʐ}�̂悤�ɁA�d�ׂ��^�����Ă��Ȃ�����̓��̋�B(�����ab�C����d)�ň͂ށB�������A���̋�A�ƒ��̋�B�͓���̓_O�𒆐S�Ƃ���B���̋�B���A���̋�A������d��̒��ɒu�����̂ŁA���̋�B�ɂ͐Ód�U���ɂ���Đ��d�ׂƕ��d�ׂ̕��z�̕肪�������B���̌��ʁA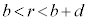 �ł́A�d��̋�����(2)�̏�Ԃ���ω��������A����ȊO�̗̈�ł͈͂ޑO�Ɠ����ł������B���̂��߁A
�ł́A�d��̋�����(2)�̏�Ԃ���ω��������A����ȊO�̗̈�ł͈͂ޑO�Ɠ����ł������B���̂��߁A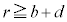 �ł́A�d�ʂ͖���������Ƃ���(2)�̏�Ԃƕς��Ȃ��B�܂��A���̋�A�ƒ��̋�B�ɋ��܂ꂽ�̈�(
�ł́A�d�ʂ͖���������Ƃ���(2)�̏�Ԃƕς��Ȃ��B�܂��A���̋�A�ƒ��̋�B�ɋ��܂ꂽ�̈�( )�ɂ����Ă��A(2)�̏�Ԃ���d�ꂪ�ω����Ă��Ȃ��̂ŁA���̗̈����2�_�Ԃł́A�d�ʍ����ω����Ȃ��B����āA���̋�B�̓����\��(
)�ɂ����Ă��A(2)�̏�Ԃ���d�ꂪ�ω����Ă��Ȃ��̂ŁA���̗̈����2�_�Ԃł́A�d�ʍ����ω����Ȃ��B����āA���̋�B�̓����\��(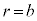 )�Ɠ��̋�A�̕\��(
)�Ɠ��̋�A�̕\��(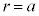 )�Ƃ̓d�ʍ�(
)�Ƃ̓d�ʍ�(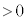 )���@�z�@�Ƌ��߂���B
)���@�z�@�Ƌ��߂���B
��1�@(3)�̏�Ԃ̓d��V�ɂ��āAr�������AV���c���Ƃ��āA�O���t��`���B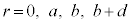 �ɂ�����V�̒l���킩��悤�ɏc���ɋL������B
�ɂ�����V�̒l���킩��悤�ɏc���ɋL������B
(4) (3)�̏�Ԃ��璆�̋���ڒn�����Ƃ���A�d�C���@�w�@���n�\�ɗ��ꂽ�B�ڒn�ɂ�蒆�̋��̓d�ʂ�0�ɂȂ�A���̋�A�̓d�ʂ��@�g�@�ɂȂ����B���̏�Ԃ̓d�ו��z�̗l�q����A���̋�A�ƒ��̋�B�̑g�ݍ��킹�́AQ�̓d�C�ʂ�~�����R���f���T�[�Ƃ݂Ȃ����Ƃ��ł���B���̃R���f���T�[�̓d�C�e�ʂ��@�`�@�ł���B
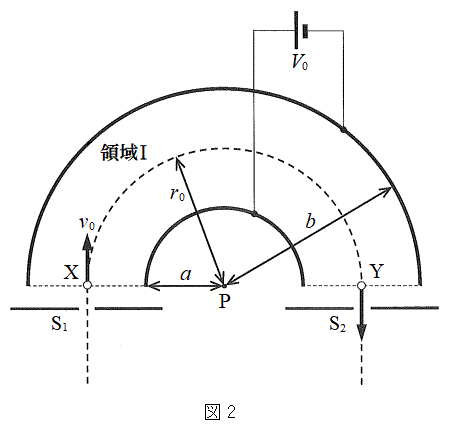 (5) �}2�̒f�ʐ}�̂悤�ɁA����̓_P�𒆐S�Ƃ���A���aa�����b (
(5) �}2�̒f�ʐ}�̂悤�ɁA����̓_P�𒆐S�Ƃ���A���aa�����b (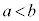 )�̔����`�́A�������ł��锖�����̂��^�ɒu����Ă���B���̑��u�𗘗p���āA���d���ʂȂǂŐ^�ɕ��o���ꂽ�d�q(����m�C�d�C��
)�̔����`�́A�������ł��锖�����̂��^�ɒu����Ă���B���̑��u�𗘗p���āA���d���ʂȂǂŐ^�ɕ��o���ꂽ�d�q(����m�C�d�C��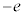 )�̉^���G�l���M�[�͂��邱�Ƃ��ł���B�����̔���(����)�ƊO������(�O��)�̊Ԃɓd�ʍ�
)�̉^���G�l���M�[�͂��邱�Ƃ��ł���B�����̔���(����)�ƊO������(�O��)�̊Ԃɓd�ʍ�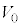 (
(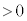 )��^����ƁA���҂ɋ��܂ꂽ�̈�(�̈�T)�ɓd�ꂪ������B�������A�����̒[�ɂ�����d��̗����A���̗̈�̓d��͖����ł���Ƃ���B���̂Ƃ��A�����ƊO���̑g�ݍ��킹�̓R���f���T�[�Ƃ݂Ȃ����Ƃ��ł���B�̈�T�ɐ�����d��̋����́A(4)�̃R���f���T�[�ɓd�ʍ�
)��^����ƁA���҂ɋ��܂ꂽ�̈�(�̈�T)�ɓd�ꂪ������B�������A�����̒[�ɂ�����d��̗����A���̗̈�̓d��͖����ł���Ƃ���B���̂Ƃ��A�����ƊO���̑g�ݍ��킹�̓R���f���T�[�Ƃ݂Ȃ����Ƃ��ł���B�̈�T�ɐ�����d��̋����́A(4)�̃R���f���T�[�ɓd�ʍ�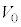 ��^�����Ƃ��̒l�Ɠ����ł���A���SP����̋���r�̊��Ƃ���r�Ca�Cb�C
��^�����Ƃ��̒l�Ɠ����ł���A���SP����̋���r�̊��Ƃ���r�Ca�Cb�C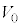 ��p�����@���@�ƕ\�����B
��p�����@���@�ƕ\�����B���ɁA�d�q���}2�̑��u�̃X���b�g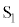 ��ʉ߂��A�_X����̈�T�ɐi�������ꍇ���l����B�������A�X���b�g�͏\���ɋ����A�}2�̂悤�ɓd�q�́A�_P�Ɠ_X�����Ԓ����ɑ��Đ����ɒʉ߂��A���ʓ����^��������̂Ƃ���B�܂��A�d�͂ƒn���C�̉e���͖����ł���Ƃ���B����̑��x
��ʉ߂��A�_X����̈�T�ɐi�������ꍇ���l����B�������A�X���b�g�͏\���ɋ����A�}2�̂悤�ɓd�q�́A�_P�Ɠ_X�����Ԓ����ɑ��Đ����ɒʉ߂��A���ʓ����^��������̂Ƃ���B�܂��A�d�͂ƒn���C�̉e���͖����ł���Ƃ���B����̑��x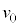 �����������́A���Ȃ킿�A����̉^���G�l���M�[
�����������́A���Ȃ킿�A����̉^���G�l���M�[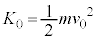 �����������̂������A�_P�𒆐S�Ƃ��铙���~�^�������A�_Y�ɓ��B������A�\�������X���b�g
�����������̂������A�_P�𒆐S�Ƃ��铙���~�^�������A�_Y�ɓ��B������A�\�������X���b�g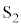 ��ʉ߂��邱�Ƃ��ł���B�����ŁA�~�O���̔��a��
��ʉ߂��邱�Ƃ��ł���B�����ŁA�~�O���̔��a��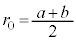 �ł���B���̂Ƃ��̓d�q�̉^���G�l���M�[
�ł���B���̂Ƃ��̓d�q�̉^���G�l���M�[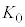 ��a�Cb�Ce�C
��a�Cb�Ce�C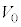 ��p�����@�k�@�ƕ\�����Ƃ��ł���B
��p�����@�k�@�ƕ\�����Ƃ��ł���B
(6) �����̕\�ʂɎ��O���Ȃǂ̌��Ă��Ƃ��̌��d���ʂ��l���悤�B���������̎��R�d�q�́A���낢��ȃG�l���M�[�������Ă���B���̃G�l���M�[�̍ő�l��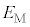 �Ƃ��A�ő�̃G�l���M�[�����d�q�������̊O�Ɏ��o�����߂ɕK�v�ȃG�l���M�[�̍ŏ��l(�d����)��W�Ƃ���B
�Ƃ��A�ő�̃G�l���M�[�����d�q�������̊O�Ɏ��o�����߂ɕK�v�ȃG�l���M�[�̍ŏ��l(�d����)��W�Ƃ���B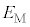 ���Ⴂ�G�l���M�[�����d�q�������̊O�Ɏ��o���ɂ́AW���傫���G�l���M�[���K�v�ł���B
���Ⴂ�G�l���M�[�����d�q�������̊O�Ɏ��o���ɂ́AW���傫���G�l���M�[���K�v�ł���B
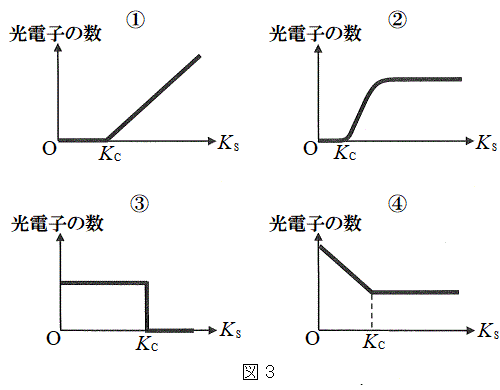 ��2�@���o���ꂽ���d�q�̐����A���d�q�̉^���G�l���M�[��
��2�@���o���ꂽ���d�q�̐����A���d�q�̉^���G�l���M�[��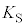 �̊��Ƃ��ĕ`�����Ƃ��A���̃O���t�̊T�`�Ƃ��čł��K�ƍl��������̂��A�}3�̇@�`�C�̂�������I�сA���̔ԍ������ɋL������B�܂��A�O���t������Â���^���G�l���M�[
�̊��Ƃ��ĕ`�����Ƃ��A���̃O���t�̊T�`�Ƃ��čł��K�ƍl��������̂��A�}3�̇@�`�C�̂�������I�сA���̔ԍ������ɋL������B�܂��A�O���t������Â���^���G�l���M�[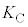 ��λ�CW�C
��λ�CW�C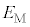 �C
�C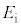 �Cc�Ch�̂����K�v�Ȃ��̂ŕ\���B
�Cc�Ch�̂����K�v�Ȃ��̂ŕ\���B
�}2�̑��u�𗘗p���āA���d�q�̉^���G�l���M�[�̕��z�����߂邱�Ƃ��ł���B���̂悤�ȕ��@�͌��d�q�����@���Ă�Ă���B
[��]
[3]�@���̕��͂�ǂ�ŁA�@�@�@�ɓK�������܂��͐��l���A���ꂼ��̉��ɋL������B�Ȃ��A�@�@�͂��ł��@�@�ŗ^����ꂽ���̂Ɠ������̂�\���B��1�C��2�ł́A�w���ɂ��������āA�����ꂼ��̉��ɋL������B�������A�~������π�Ƃ��A�p�x�̒P�ʂɂ̓��W�A����p����B
�Ό��̓f�B�X�v���[����ʐM�A���ʎq�Z�p�ȂǗl�X�ȕ���ŗ��p����Ă���B���̕Ό��𑀍삷����@�ɂ��čl���Ă݂悤�B
���͓d���g�̈��ł���A�d��Ǝ��ꂪ���̐i�s�����Ɛ����ɐU�����Ȃ���`���B�d��̐U������������A�����ł͕Ό��̕����ƌĂԁB�d��̓x�N�g���ł���A�قȂ�2�̕����̐����ɕ������A�܂��������čl���邱�Ƃ��ł���B�Ό��́A�������̕���(���ߎ��ƌĂ�)�ƕ��s�ɐU������d�ꐬ�����Ȃ����߂��A���ߎ��Ɛ����ɐU������d�ꐬ�������S�ɎՒf����Ƃ���B�܂��ȉ��ōl��������o��̐M�����xI �́A�Ό��̕����Ɉˑ������A���˂�����̓d��̐U����2��ɔ�Ⴗ����̂Ƃ���B
�Ȃ��A�Ό�������o�킨��ь�q���铧�����̂́A���̕\�ʂ����̐i�s�����Ɛ����ɂȂ�悤�ɐ^�ɒu����Ă���A�\�ʂɂ�������̈ʑ��̕ω��┽�˂͖�������B�܂��A�ȉ��ł̓��ˌ��̔g���̒l�͐^�ł̒l�Ƃ���B
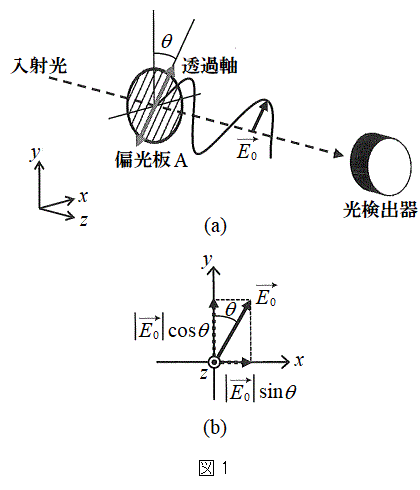 ���܁A�}1(a)�̂悤�ɁA�g����
���܁A�}1(a)�̂悤�ɁA�g����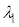 �̒P�F�̓��ˌ����A�Ό���A��ʉ߂�������A�����o��Ō��o�����Bz�������̐i�s�����Ƃ��Đ}1(a)�̍����̂悤��x����y�����Ƃ�A�Ό��̓��ߎ���y���̂Ȃ��p�x��θ�Ƃ���B�Ό���
�̒P�F�̓��ˌ����A�Ό���A��ʉ߂�������A�����o��Ō��o�����Bz�������̐i�s�����Ƃ��Đ}1(a)�̍����̂悤��x����y�����Ƃ�A�Ό��̓��ߎ���y���̂Ȃ��p�x��θ�Ƃ���B�Ό���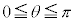 �͈̔͂ŁAxy���ʓ��ʼn�]�ł���B���ˌ��ɂ͂��낢��ȕ����ɐU�����������l�Ɋ܂܂�Ă���B���̂��߁Aθ����L�͈̔͂ŕω��������Ƃ��A�����o��̐M�����x��
�͈̔͂ŁAxy���ʓ��ʼn�]�ł���B���ˌ��ɂ͂��낢��ȕ����ɐU�����������l�Ɋ܂܂�Ă���B���̂��߁Aθ����L�͈̔͂ŕω��������Ƃ��A�����o��̐M�����x��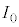 �ŏ�Ɉ��ł������B�܂��A���̔g���̓��ˌ���p�����ꍇ�ɂ����l�̌��ʂ�����ꂽ�B�Ό���A��ʉ߂�����̌��̏�Ԃ́A���̑傫�����d��̐U���ŁA���̌������d��̌����ƈ�v����x�N�g��
�ŏ�Ɉ��ł������B�܂��A���̔g���̓��ˌ���p�����ꍇ�ɂ����l�̌��ʂ�����ꂽ�B�Ό���A��ʉ߂�����̌��̏�Ԃ́A���̑傫�����d��̐U���ŁA���̌������d��̌����ƈ�v����x�N�g��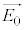 (�ȉ��A�����U���x�N�g���ƌĂ�)��p���ē����Â�����B�}1(b)�Ɏ����悤�ɁA
(�ȉ��A�����U���x�N�g���ƌĂ�)��p���ē����Â�����B�}1(b)�Ɏ����悤�ɁA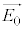 ��x�������̐�����y�������̐����ɕ������čl���邱�Ƃ��ł��A
��x�������̐�����y�������̐����ɕ������čl���邱�Ƃ��ł��A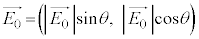 �ƕ\����B�Ȃ��}1(b)�ł͎��ʂ̗�����\�̌�����z���̐��̕����Ƃ���B
�ƕ\����B�Ȃ��}1(b)�ł͎��ʂ̗�����\�̌�����z���̐��̕����Ƃ���B
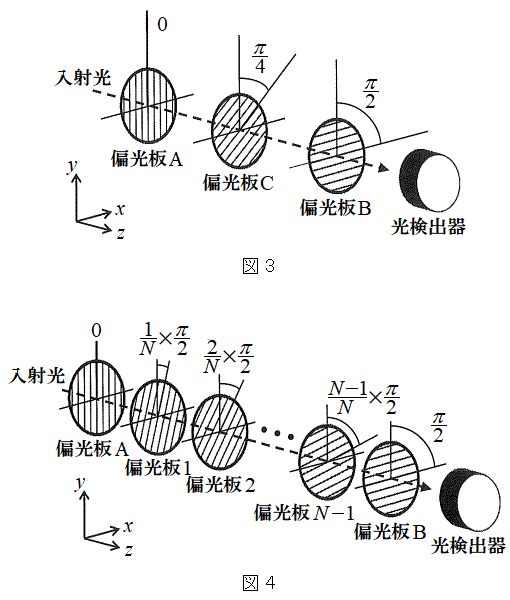 (2) �Ό��̕����𑀍삷����@�Ƃ��āA�Ό��݂̂�p������@�ɂ��čl���悤�B�}3�̂悤�ɁA�Ό���A�̊p�x��0�C�Ό���B�̊p�x��
(2) �Ό��̕����𑀍삷����@�Ƃ��āA�Ό��݂̂�p������@�ɂ��čl���悤�B�}3�̂悤�ɁA�Ό���A�̊p�x��0�C�Ό���B�̊p�x��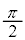 �ɌŒ肵�A���̊ԂɕΌ���C���A�p�x��
�ɌŒ肵�A���̊ԂɕΌ���C���A�p�x��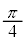 �ɂ��Đݒu�����B�g��
�ɂ��Đݒu�����B�g��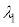 �̌�����˂����Ƃ��̌����o��̐M�����xI �́A�@���@�~
�̌�����˂����Ƃ��̌����o��̐M�����xI �́A�@���@�~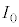 �ł���B
�ł���B
���ɐ}4�̂悤�ɁA�Ό���A�̊p�x��0�C�Ό���B�̊p�x��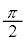 �ɌŒ肵�A���̊ԂɕΌ���
�ɌŒ肵�A���̊ԂɕΌ���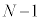 (N��2�ȏ�̐���)���ݒu�����B�Ό���A�ɋ߂����̂��珇�ɕΌ���k (
(N��2�ȏ�̐���)���ݒu�����B�Ό���A�ɋ߂����̂��珇�ɕΌ���k (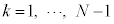 )�ƌĂсA�Ό���k�̊p�x��
)�ƌĂсA�Ό���k�̊p�x��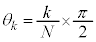 �ɐݒ肷��B�g��
�ɐݒ肷��B�g��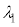 �̌�����˂����Ƃ��̌����o��̐M�����xI �́A�@���@�~
�̌�����˂����Ƃ��̌����o��̐M�����xI �́A�@���@�~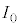 �ł���A
�ł���A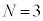 �̂Ƃ��ɂ��@���@�~
�̂Ƃ��ɂ��@���@�~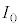 �ƂȂ�B
�ƂȂ�B
�����N��1���\���傫���ꍇ�ɂ��čl���Ă݂悤�B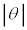 ��1���\��������(
��1���\��������(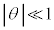 )�Ƃ�
)�Ƃ�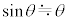 �Ƌߎ��ł��A�܂�a��萔�Ƃ���
�Ƌߎ��ł��A�܂�a��萔�Ƃ���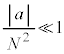 �̂Ƃ�
�̂Ƃ�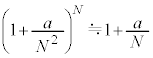 �Ƌߎ��ł��邱�Ƃ�p����ƁA�@���@�~
�Ƌߎ��ł��邱�Ƃ�p����ƁA�@���@�~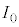 ��
�� �Ƌߎ��ł���B���̂��Ƃ���A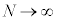 �̋Ɍ��ł̌����o��̐M�����xI �́A
�̋Ɍ��ł̌����o��̐M�����xI �́A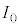 �ɑQ�߂��邱�Ƃ��킩��B���̌��ʂ��A�����x�������������ɕΌ��̕������p�x
�ɑQ�߂��邱�Ƃ��킩��B���̌��ʂ��A�����x�������������ɕΌ��̕������p�x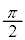 ������]�����邱�Ƃ��A�����I�ɕΌ��݂̂�p���ĉ\�ł���Ƃ����A�����[�����_��������B
������]�����邱�Ƃ��A�����I�ɕΌ��݂̂�p���ĉ\�ł���Ƃ����A�����[�����_��������B
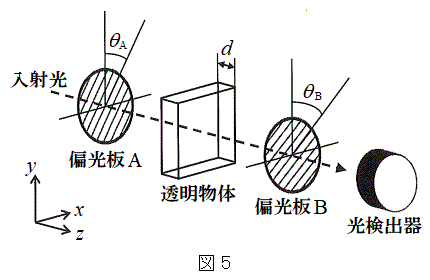 (3) �Ό��̕����𑀍삷��ʂ̕��@�Ƃ��āA���̕Ό��̕����ɂ���ċ��ܗ����قȂ铧���Ȕ}����p������@�ɂ��čl���悤�B�}5�̂悤�ɁA�Ό���A�ƕΌ���B�̊ԂɁA���̂悤�Ȕ}������Ȃ钼���̂̓������̂�}�������ꍇ���l����B���̌��̐i�s�����̌��݂�d�C���̓d��̐U��������x�������̏ꍇ�̋��ܗ���
(3) �Ό��̕����𑀍삷��ʂ̕��@�Ƃ��āA���̕Ό��̕����ɂ���ċ��ܗ����قȂ铧���Ȕ}����p������@�ɂ��čl���悤�B�}5�̂悤�ɁA�Ό���A�ƕΌ���B�̊ԂɁA���̂悤�Ȕ}������Ȃ钼���̂̓������̂�}�������ꍇ���l����B���̌��̐i�s�����̌��݂�d�C���̓d��̐U��������x�������̏ꍇ�̋��ܗ��� �Cy�������̏ꍇ��
�Cy�������̏ꍇ��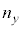 �Ƃ��A�����̋��ܗ��͌��̔g���ɂ�炸���ŁA�݂��ɈقȂ�
�Ƃ��A�����̋��ܗ��͌��̔g���ɂ�炸���ŁA�݂��ɈقȂ�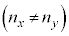 �Ƃ���B�܂��A���̓������̒��ł́A���͕Ό��̕����ɂ�炸�����o�H�i���A���̋z���͖����ł���Ƃ���B
�Ƃ���B�܂��A���̓������̒��ł́A���͕Ό��̕����ɂ�炸�����o�H�i���A���̋z���͖����ł���Ƃ���B���ܕΌ���A�̊p�x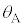 �ƕΌ���B�̊p�x
�ƕΌ���B�̊p�x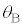 ���Ƃ���
���Ƃ���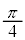 �ɐݒ肵�A�g��
�ɐݒ肵�A�g��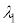 �̌�����˂���ƁA�����o��̐M�����x��0�ɂȂ����B���̂悤�ȏɂȂ铧�����̂̍ŏ��̌��݂����߂Ă݂悤�B
�̌�����˂���ƁA�����o��̐M�����x��0�ɂȂ����B���̂悤�ȏɂȂ铧�����̂̍ŏ��̌��݂����߂Ă݂悤�B
�Ό���A��ʉ߂������̕Ό�������y���ƂȂ��p�x��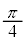 �ł���A�d���x������������y�����������́A���ꂼ��̐U����
�ł���A�d���x������������y�����������́A���ꂼ��̐U����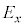 �C
�C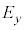 �Ƃ��ē��ʑ�(�ʑ���0)�ŐU�����Ă���B�������̕����̌��H���͓d���x�����������ɑ��Ă��@���@�Cy�����������ɑ��Ă��@���@�ł���A�����̌��H��(
�Ƃ��ē��ʑ�(�ʑ���0)�ŐU�����Ă���B�������̕����̌��H���͓d���x�����������ɑ��Ă��@���@�Cy�����������ɑ��Ă��@���@�ł���A�����̌��H��(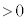 )���@���@�ŗ^������B���̌��H�����A
)���@���@�ŗ^������B���̌��H�����A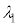 �����0�ȏ�̐���m��p�����@���@�ƕ\�����Ƃ��A�������̂�ʉ߂�����̓d���x������������y�����������͋t�ʑ�(�ʑ���π)�ƂȂ�B���̂Ƃ��A�d��̐U���x�N�g����x�������������A�������̂�ʉ߂���O�ƕς�炸
�����0�ȏ�̐���m��p�����@���@�ƕ\�����Ƃ��A�������̂�ʉ߂�����̓d���x������������y�����������͋t�ʑ�(�ʑ���π)�ƂȂ�B���̂Ƃ��A�d��̐U���x�N�g����x�������������A�������̂�ʉ߂���O�ƕς�炸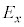 ���Ƃ���Ay�����������́A���������]��
���Ƃ���Ay�����������́A���������]��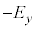 �ƂȂ�B�����̐������x�N�g���Ƃ��č�������錋�ʁA�Ό�������y���ƂȂ��p�x��
�ƂȂ�B�����̐������x�N�g���Ƃ��č�������錋�ʁA�Ό�������y���ƂȂ��p�x��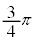 �ƂȂ�A�Ό���B�̓��ߎ��ƒ������A���o��̏o�͂�0�ƂȂ�B���̏��������������̂̍ŏ��̌���
�ƂȂ�A�Ό���B�̓��ߎ��ƒ������A���o��̏o�͂�0�ƂȂ�B���̏��������������̂̍ŏ��̌���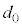 ��
��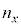 �C
�C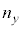 �C
�C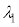 ��p���ĕ\���ƁA
��p���ĕ\���ƁA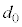 ���@���@�ł���B
���@���@�ł���B
��1�@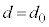 �̂Ƃ��A�Ό���A�ƕΌ���B�̊p�x���Ƃ���θ�Ƃ��āAθ��0����
�̂Ƃ��A�Ό���A�ƕΌ���B�̊p�x���Ƃ���θ�Ƃ��āAθ��0����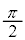 �܂ŕω��������ۂ̌����o��̐M�����xI �̕ω����A�O���t�ɕ`���B���̍ہAθ�������A�����o��̐M�����xI ���c���ɂƂ�A�M�����xI �̍ő�l�A�ŏ��l�ƁA���ꂼ��ɑΉ�����θ�̒l��������悤�ɐ}������B
�܂ŕω��������ۂ̌����o��̐M�����xI �̕ω����A�O���t�ɕ`���B���̍ہAθ�������A�����o��̐M�����xI ���c���ɂƂ�A�M�����xI �̍ő�l�A�ŏ��l�ƁA���ꂼ��ɑΉ�����θ�̒l��������悤�ɐ}������B
(4) (3)�̏ŁA�}5�̕Ό���A�̊p�x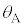 �ƕΌ���B�̊p�x
�ƕΌ���B�̊p�x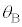 ���Ƃ���
���Ƃ���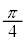 �ɐݒ肵�A����ǂ͌��݂�
�ɐݒ肵�A����ǂ͌��݂�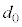 ��20�{(
��20�{(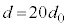 )�̓���̓������̂�ݒu���āA�g��
)�̓���̓������̂�ݒu���āA�g��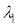 �̌�����˂����B���̂Ƃ��A�����o��̐M�����x���@���@�~
�̌�����˂����B���̂Ƃ��A�����o��̐M�����x���@���@�~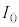 �ƂȂ����B
�ƂȂ����B
��2�@(4)�̏ŁA���ˌ��Ƃ��Ĕg����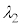 �̒P�F�̌���p����ƁA�M�����x��0�ƂȂ����B���̂悤�ȓ��ˌ��̔g��
�̒P�F�̌���p����ƁA�M�����x��0�ƂȂ����B���̂悤�ȓ��ˌ��̔g��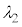 �͕����l������B
�͕����l������B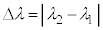 �Ƃ��āA�ŏ���
�Ƃ��āA�ŏ���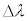 ���A
���A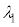 ��p���ĕ\���B���o�ߒ��������B
��p���ĕ\���B���o�ߒ��������B
�ȏ�Œ��ׂ��A���ܗ����قȂ镨���ɂ�����Ό������̕ω��́A�����̐�������ׂ݂�Ό��������Ȃǂł����p����Ă���B
[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 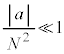 �̂Ƃ�
�̂Ƃ�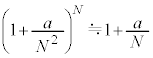 �Ƌߎ��ł��邱�Ƃ�p����ƁA�@���@�~
�Ƌߎ��ł��邱�Ƃ�p����ƁA�@���@�~