���啨��'23�N�O��[2]
���̕��͂�ǂ�ŁA�@�@�ɓK�������܂��͐��l���A{�@�@}����͓K�Ȃ��̂���I�т��̔ԍ����A���ꂼ��̉��ɋL������B�Ȃ��A�@�@�͂��ł��@�@�ŗ^����ꂽ���̂Ɠ������̂�\���B�܂��A��1�C��2�ł́A�w���ɂ��������āA�����ꂼ��̉��ɋL������B�������A�^�̃N�[�����̖@���̔��萔��k�C�~������π�Ƃ���B
(1) �^�ɒu���ꂽ���̓d�C��Q�̓_�d�ׂ���o��d�C�͐��̖{�����l����B�_�d�ׂ𒆐S�Ƃ��鋅�ʂ��l����ƁA���̋��ʂ��т��P�ʖʐς�����̓d�C�͐��̖{��(�d�C�͐��̖��x)�́A�d��̋����Ɠ������Ȃ�悤�ɒ�߂��Ă���B���̂��Ƃ���A�_�d�ׂ���o��d�C�͐��̖{�����@�C�@�ł���B
(2) �^�ɂ��锼�aa�̓��̋�A�ɐ��̓d�C��Q��^����ƁA�d�ׂ�{���F�@�����S�̂ɁC�A���̕\�ʂ�}��l�ɕ��z����B���̒��SO���狗��r�̋��ʂ��т��d�C�͐��̖{����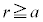 �ł��@�C�@�ŁA�d�C��Q�̓_�d�ׂ𒆐SO�ɒu�����Ƃ��Ɠ����ł���B���̂��߁A�d��̋����Ɠd�ʂ́A�_�d�ׂ̏ꍇ�ƕς��Ȃ��B����A
�ł��@�C�@�ŁA�d�C��Q�̓_�d�ׂ𒆐SO�ɒu�����Ƃ��Ɠ����ł���B���̂��߁A�d��̋����Ɠd�ʂ́A�_�d�ׂ̏ꍇ�ƕς��Ȃ��B����A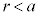 �ł͓d��̋������@�n�@�ŁA�d�ʂ��@�j�@�ƂȂ�B�������A��������d�ʂ̊(�d�ʁ�0)�Ƃ���B
�ł͓d��̋������@�n�@�ŁA�d�ʂ��@�j�@�ƂȂ�B�������A��������d�ʂ̊(�d�ʁ�0)�Ƃ���B
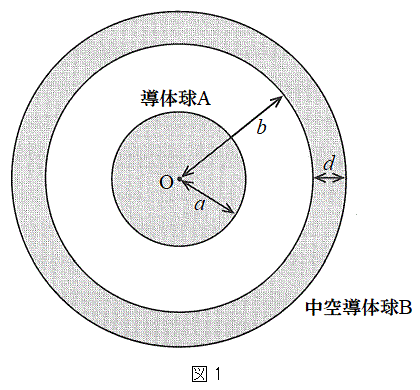 (3) (2)�̏�Ԃɂ��铱�̋�A���A�}1�̒f�ʐ}�̂悤�ɁA�d�ׂ��^�����Ă��Ȃ�����̓��̋�B(�����ab�C����d)�ň͂ށB�������A���̋�A�ƒ��̋�B�͓���̓_O�𒆐S�Ƃ���B���̋�B���A���̋�A������d��̒��ɒu�����̂ŁA���̋�B�ɂ͐Ód�U���ɂ���Đ��d�ׂƕ��d�ׂ̕��z�̕肪�������B���̌��ʁA
(3) (2)�̏�Ԃɂ��铱�̋�A���A�}1�̒f�ʐ}�̂悤�ɁA�d�ׂ��^�����Ă��Ȃ�����̓��̋�B(�����ab�C����d)�ň͂ށB�������A���̋�A�ƒ��̋�B�͓���̓_O�𒆐S�Ƃ���B���̋�B���A���̋�A������d��̒��ɒu�����̂ŁA���̋�B�ɂ͐Ód�U���ɂ���Đ��d�ׂƕ��d�ׂ̕��z�̕肪�������B���̌��ʁA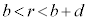 �ł́A�d��̋�����(2)�̏�Ԃ���ω��������A����ȊO�̗̈�ł͈͂ޑO�Ɠ����ł������B���̂��߁A
�ł́A�d��̋�����(2)�̏�Ԃ���ω��������A����ȊO�̗̈�ł͈͂ޑO�Ɠ����ł������B���̂��߁A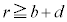 �ł́A�d�ʂ͖���������Ƃ���(2)�̏�Ԃƕς��Ȃ��B�܂��A���̋�A�ƒ��̋�B�ɋ��܂ꂽ�̈�(
�ł́A�d�ʂ͖���������Ƃ���(2)�̏�Ԃƕς��Ȃ��B�܂��A���̋�A�ƒ��̋�B�ɋ��܂ꂽ�̈�(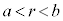 )�ɂ����Ă��A(2)�̏�Ԃ���d�ꂪ�ω����Ă��Ȃ��̂ŁA���̗̈����2�_�Ԃł́A�d�ʍ����ω����Ȃ��B����āA���̋�B�̓����\��(
)�ɂ����Ă��A(2)�̏�Ԃ���d�ꂪ�ω����Ă��Ȃ��̂ŁA���̗̈����2�_�Ԃł́A�d�ʍ����ω����Ȃ��B����āA���̋�B�̓����\��(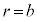 )�Ɠ��̋�A�̕\��(
)�Ɠ��̋�A�̕\��(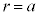 )�Ƃ̓d�ʍ�(
)�Ƃ̓d�ʍ�(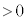 )���@�z�@�Ƌ��߂���B
)���@�z�@�Ƌ��߂���B
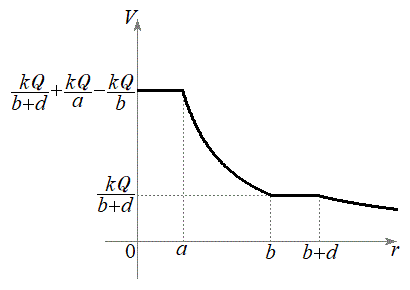
��1�@(3)�̏�Ԃ̓d��V�ɂ��āAr�������AV���c���Ƃ��āA�O���t��`���B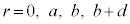 �ɂ�����V�̒l���킩��悤�ɏc���ɋL������B
�ɂ�����V�̒l���킩��悤�ɏc���ɋL������B
(4) (3)�̏�Ԃ��璆�̋���ڒn�����Ƃ���A�d�C���@�w�@���n�\�ɗ��ꂽ�B�ڒn�ɂ�蒆�̋��̓d�ʂ�0�ɂȂ�A���̋�A�̓d�ʂ��@�g�@�ɂȂ����B���̏�Ԃ̓d�ו��z�̗l�q����A���̋�A�ƒ��̋�B�̑g�ݍ��킹�́AQ�̓d�C�ʂ�~�����R���f���T�[�Ƃ݂Ȃ����Ƃ��ł���B���̃R���f���T�[�̓d�C�e�ʂ��@�`�@�ł���B
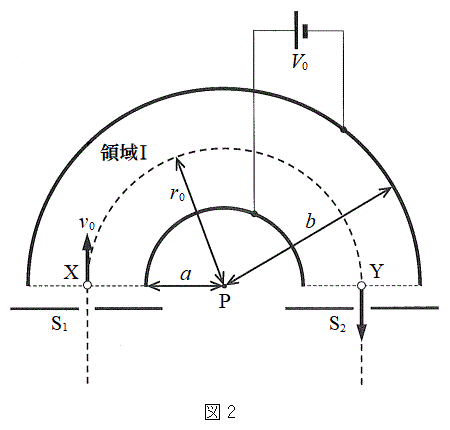 (5) �}2�̒f�ʐ}�̂悤�ɁA����̓_P�𒆐S�Ƃ���A���aa�����b (
(5) �}2�̒f�ʐ}�̂悤�ɁA����̓_P�𒆐S�Ƃ���A���aa�����b (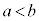 )�̔����`�́A�������ł��锖�����̂��^�ɒu����Ă���B���̑��u�𗘗p���āA���d���ʂȂǂŐ^�ɕ��o���ꂽ�d�q(����m�C�d�C��
)�̔����`�́A�������ł��锖�����̂��^�ɒu����Ă���B���̑��u�𗘗p���āA���d���ʂȂǂŐ^�ɕ��o���ꂽ�d�q(����m�C�d�C��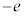 )�̉^���G�l���M�[�͂��邱�Ƃ��ł���B�����̔���(����)�ƊO������(�O��)�̊Ԃɓd�ʍ�
)�̉^���G�l���M�[�͂��邱�Ƃ��ł���B�����̔���(����)�ƊO������(�O��)�̊Ԃɓd�ʍ�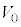 (
(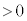 )��^����ƁA���҂ɋ��܂ꂽ�̈�(�̈�T)�ɓd�ꂪ������B�������A�����̒[�ɂ�����d��̗����A���̗̈�̓d��͖����ł���Ƃ���B���̂Ƃ��A�����ƊO���̑g�ݍ��킹�̓R���f���T�[�Ƃ݂Ȃ����Ƃ��ł���B�̈�T�ɐ�����d��̋����́A(4)�̃R���f���T�[�ɓd�ʍ�
)��^����ƁA���҂ɋ��܂ꂽ�̈�(�̈�T)�ɓd�ꂪ������B�������A�����̒[�ɂ�����d��̗����A���̗̈�̓d��͖����ł���Ƃ���B���̂Ƃ��A�����ƊO���̑g�ݍ��킹�̓R���f���T�[�Ƃ݂Ȃ����Ƃ��ł���B�̈�T�ɐ�����d��̋����́A(4)�̃R���f���T�[�ɓd�ʍ�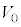 ��^�����Ƃ��̒l�Ɠ����ł���A���SP����̋���r�̊��Ƃ���r�Ca�Cb�C
��^�����Ƃ��̒l�Ɠ����ł���A���SP����̋���r�̊��Ƃ���r�Ca�Cb�C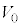 ��p�����@���@�ƕ\�����B
��p�����@���@�ƕ\�����B���ɁA�d�q���}2�̑��u�̃X���b�g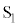 ��ʉ߂��A�_X����̈�T�ɐi�������ꍇ���l����B�������A�X���b�g�͏\���ɋ����A�}2�̂悤�ɓd�q�́A�_P�Ɠ_X�����Ԓ����ɑ��Đ����ɒʉ߂��A���ʓ����^��������̂Ƃ���B�܂��A�d�͂ƒn���C�̉e���͖����ł���Ƃ���B����̑��x
��ʉ߂��A�_X����̈�T�ɐi�������ꍇ���l����B�������A�X���b�g�͏\���ɋ����A�}2�̂悤�ɓd�q�́A�_P�Ɠ_X�����Ԓ����ɑ��Đ����ɒʉ߂��A���ʓ����^��������̂Ƃ���B�܂��A�d�͂ƒn���C�̉e���͖����ł���Ƃ���B����̑��x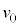 �����������́A���Ȃ킿�A����̉^���G�l���M�[
�����������́A���Ȃ킿�A����̉^���G�l���M�[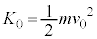 �����������̂������A�_P�𒆐S�Ƃ��铙���~�^�������A�_Y�ɓ��B������A�\�������X���b�g
�����������̂������A�_P�𒆐S�Ƃ��铙���~�^�������A�_Y�ɓ��B������A�\�������X���b�g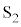 ��ʉ߂��邱�Ƃ��ł���B�����ŁA�~�O���̔��a��
��ʉ߂��邱�Ƃ��ł���B�����ŁA�~�O���̔��a��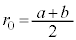 �ł���B���̂Ƃ��̓d�q�̉^���G�l���M�[
�ł���B���̂Ƃ��̓d�q�̉^���G�l���M�[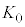 ��a�Cb�Ce�C
��a�Cb�Ce�C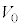 ��p�����@�k�@�ƕ\�����Ƃ��ł���B
��p�����@�k�@�ƕ\�����Ƃ��ł���B
(6) �����̕\�ʂɎ��O���Ȃǂ̌��Ă��Ƃ��̌��d���ʂ��l���悤�B���������̎��R�d�q�́A���낢��ȃG�l���M�[�������Ă���B���̃G�l���M�[�̍ő�l��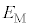 �Ƃ��A�ő�̃G�l���M�[�����d�q�������̊O�Ɏ��o�����߂ɕK�v�ȃG�l���M�[�̍ŏ��l(�d����)��W�Ƃ���B
�Ƃ��A�ő�̃G�l���M�[�����d�q�������̊O�Ɏ��o�����߂ɕK�v�ȃG�l���M�[�̍ŏ��l(�d����)��W�Ƃ���B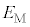 ���Ⴂ�G�l���M�[�����d�q�������̊O�Ɏ��o���ɂ́AW���傫���G�l���M�[���K�v�ł���B
���Ⴂ�G�l���M�[�����d�q�������̊O�Ɏ��o���ɂ́AW���傫���G�l���M�[���K�v�ł���B
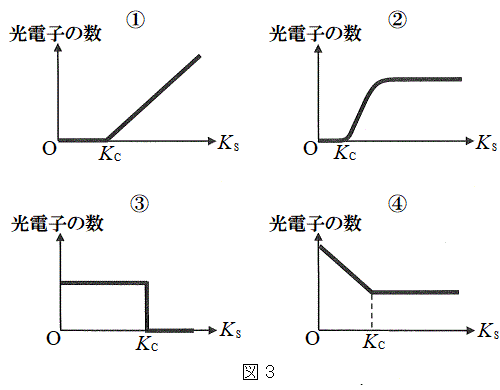 ��2�@���o���ꂽ���d�q�̐����A���d�q�̉^���G�l���M�[��
��2�@���o���ꂽ���d�q�̐����A���d�q�̉^���G�l���M�[��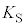 �̊��Ƃ��ĕ`�����Ƃ��A���̃O���t�̊T�`�Ƃ��čł��K�ƍl��������̂��A�}3�̇@�`�C�̂�������I�сA���̔ԍ������ɋL������B�܂��A�O���t������Â���^���G�l���M�[
�̊��Ƃ��ĕ`�����Ƃ��A���̃O���t�̊T�`�Ƃ��čł��K�ƍl��������̂��A�}3�̇@�`�C�̂�������I�сA���̔ԍ������ɋL������B�܂��A�O���t������Â���^���G�l���M�[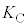 ��λ�CW�C
��λ�CW�C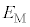 �C
�C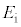 �Cc�Ch�̂����K�v�Ȃ��̂ŕ\���B
�Cc�Ch�̂����K�v�Ȃ��̂ŕ\���B
�}2�̑��u�𗘗p���āA���d�q�̉^���G�l���M�[�̕��z�����߂邱�Ƃ��ł���B���̂悤�ȕ��@�͌��d�q�����@���Ă�Ă���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�O���ŁA�����`�̑��u���̓d��̏��l�@���A�Ō�Ɍ��d���ʂɂ����o���ꂽ���d�q�̃G�l���M�[���l���悤�A�Ƃ������ł��B
���邢�́A�N�[�����̖@���ɂ��A���d��Q���狗��r���ꂽ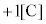 �̓d�ׂ���d�C�͂�
�̓d�ׂ���d�C�͂�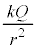 �ł��邱�Ƃ���A���d��Q���狗��r���ꂽ�_�ɂ������d��̋�����
�ł��邱�Ƃ���A���d��Q���狗��r���ꂽ�_�ɂ������d��̋�����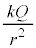 �C���d��Q����N�{�̓d�C�͐����L�т�A�Ƃ��āA�d�C�͐��̖��x(���ar�̋��ʂ̖ʐς�
�C���d��Q����N�{�̓d�C�͐����L�т�A�Ƃ��āA�d�C�͐��̖��x(���ar�̋��ʂ̖ʐς�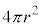 )���d��̋����ɓ��������Ƃ���
)���d��̋����ɓ��������Ƃ���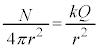 �@��
�@�� 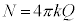
(2) ���̋������ł͓d�ׂ͎��R�ɓ����܂����A�d�Ԃɐ˗͂������A�d�ׂ݂͌��̋������ő剻���悤�Ƃ���̂ŁA�d�ׂ͓��̋��\�ʂɈ�l�ɕ��z���܂��B�@�A ......[��]
�d�C�͐��̖{���́A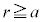 �ł�(1)�̏ƕς�炸
�ł�(1)�̏ƕς�炸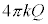 �{�ŁA�d��̋�����(1)�ƕς�炸
�{�ŁA�d��̋�����(1)�ƕς�炸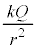 �ŁA����������Ƃ���d�ʂ�
�ŁA����������Ƃ���d�ʂ�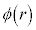 �Ƃ���ƁA�d�ʂ�
�Ƃ���ƁA�d�ʂ�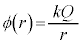 (�d�ʁE�d�����Q��)�ł��B
(�d�ʁE�d�����Q��)�ł��B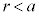 �ł͔��ar�̋����ɓd�ׂ͑��݂����A�d��̋�����0�ł��B�@0 ......[�n]���̋������ɓd�ׂ͑��݂����A���̋������ł͓���d�ʂɂȂ�܂��B���aa�̓��̋��\�ʂł́A���̒��S�ɓd�ׂ����݂��Ă���ꍇ�Ɠ������d�ʂ�
�ł͔��ar�̋����ɓd�ׂ͑��݂����A�d��̋�����0�ł��B�@0 ......[�n]���̋������ɓd�ׂ͑��݂����A���̋������ł͓���d�ʂɂȂ�܂��B���aa�̓��̋��\�ʂł́A���̒��S�ɓd�ׂ����݂��Ă���ꍇ�Ɠ������d�ʂ�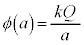 �ŁA���̓���(
�ŁA���̓���(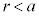 )�ł͓���d�ʂȂ̂œd�ʂ�
)�ł͓���d�ʂȂ̂œd�ʂ�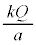 �ł��B�@
�ł��B�@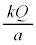 ......[�j]
......[�j]
(3) ���X�d�ׂ��^�����Ă��Ȃ��������̋�B�̓����\�ʂɂ��Ód�U���ɂ�蕉�d��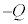 �����z���O���\�ʂɂ͐��d��
�����z���O���\�ʂɂ͐��d��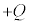 �����z���܂��B
�����z���܂��B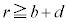 �ɂ����Ă�(2)�̏�Ԃƕς�炸�A�d��̋�����
�ɂ����Ă�(2)�̏�Ԃƕς�炸�A�d��̋�����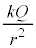 �C�d�ʂ�
�C�d�ʂ�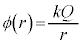 �ł��B���̋�B�̓���(
�ł��B���̋�B�̓���(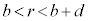 )�ł͓d��͑��݂������d�ʂł��B���̋�B�̊O���\�ʂł͓d�ʂ�
)�ł͓d��͑��݂������d�ʂł��B���̋�B�̊O���\�ʂł͓d�ʂ�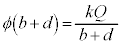 �C���̋�B�̓���(
�C���̋�B�̓���(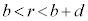 )�ł�
)�ł�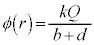 �ł��B
�ł��B
 ��1�@���̋�B�̊O��(
��1�@���̋�B�̊O��(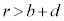 )�ł͓d��V��
)�ł͓d��V��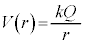 �ł��B���̋�B�̊O���\��(
�ł��B���̋�B�̊O���\��(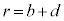 )�̓d�ʂ�
)�̓d�ʂ�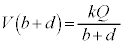 �Œ��̋�B�̓���(
�Œ��̋�B�̓���(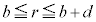 )�ł͓��d�ʁA�����\��(
)�ł͓��d�ʁA�����\��(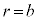 )�̓d�ʂ�
)�̓d�ʂ�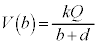 �ł��B���̋�A�̕\��(
�ł��B���̋�A�̕\��(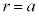 )�ɂ�����d��
)�ɂ�����d��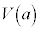 �́A
�́A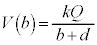 ����[�z]�̓d�ʍ�
����[�z]�̓d�ʍ�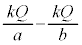 ��������
��������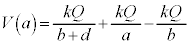 �ŁA���̋�A�̓���(
�ŁA���̋�A�̓���(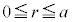 )�ł͓��d�ʂł��B�����(3)�̏�Ԃ̓d��V�̃O���t�͉E�}�B
)�ł͓��d�ʂł��B�����(3)�̏�Ԃ̓d��V�̃O���t�͉E�}�B���D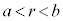 �ɂ�����d��
�ɂ�����d��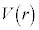 �́A���̗̈�ł̓d��̋�����
�́A���̗̈�ł̓d��̋�����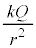 �ł��邱�Ƃ���A�d�ꂪ�y�ڂ��d�C�͂ɋt�炤�O�͂�����d���Ƃ��āA
�ł��邱�Ƃ���A�d�ꂪ�y�ڂ��d�C�͂ɋt�炤�O�͂�����d���Ƃ��āA �ƂȂ�܂��B
(4) (3)�Œ��̋�B�ɐ������d�ׂ̂����A���̋�A�ƑΌ����Ă�������\�ʂ̓d��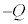 �́A���̋��\�ʂ̓d��
�́A���̋��\�ʂ̓d��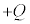 �ƈ��������Ă��邽�ߓ����܂���B�O���\�ʂɕ��z���Ă����d��
�ƈ��������Ă��邽�ߓ����܂���B�O���\�ʂɕ��z���Ă����d��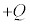 ���n�\�ɗ���܂��B�@Q ......[�w]
���n�\�ɗ���܂��B�@Q ......[�w] ���̋�B�̓d�ʂ�0�ɂȂ�A����������̋�A�̓d�ʂ�[�z]�ɂ��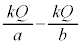 ���������A���̋��̓d�ʂ�
���������A���̋��̓d�ʂ�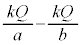 �ł��B�@
�ł��B�@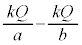 ......[�g]�R���f���T�[�̐Ód�e�ʂ�C�Ƃ��āA
......[�g]�R���f���T�[�̐Ód�e�ʂ�C�Ƃ��āA 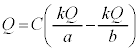 �@��
�@�� 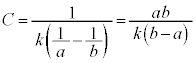 ......[�`]
......[�`]
(5) �̈�T���̒��S���狗��r�̈ʒu�ɂ�����d��̋�����(2)�Ɠ��l��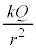 �ł����AQ���g�킸a�Cb�C
�ł����AQ���g�킸a�Cb�C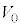 ��p���ĕ\���̂ŁA[�`]�̌��ʂ��A
��p���ĕ\���̂ŁA[�`]�̌��ʂ��A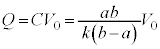 �@����@
�@����@ ��p���āA
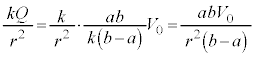 ......[��]
......[��]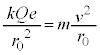 �@��
�@�� 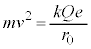
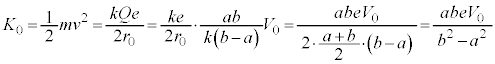 ......[�k]
......[�k]
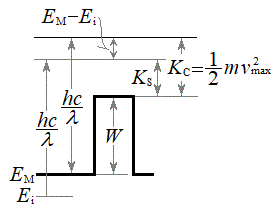 (6) ���낢��ȃG�l���M�[���o�Ă��ĕ���킵���ł����A�d�q�̃G�l���M�[
(6) ���낢��ȃG�l���M�[���o�Ă��ĕ���킵���ł����A�d�q�̃G�l���M�[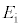 �C�d�q�̍ő�G�l���M�[
�C�d�q�̍ő�G�l���M�[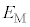 �C�d����W�C���q�̃G�l���M�[
�C�d����W�C���q�̃G�l���M�[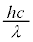 �C���o���ꂽ���d�q�̉^���G�l���M�[
�C���o���ꂽ���d�q�̉^���G�l���M�[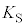 �̊W�͉E�}�̂悤�ɂȂ��Ă��܂�(���d�������Q��)�B�Ȃ��A���o���ꂽ���d�q�̉^���G�l���M�[�̍ő�l
�̊W�͉E�}�̂悤�ɂȂ��Ă��܂�(���d�������Q��)�B�Ȃ��A���o���ꂽ���d�q�̉^���G�l���M�[�̍ő�l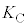 �́A
�́A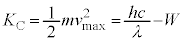 �@����A
�@����A�ƂȂ�܂��B���o�������d�q��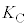 ���傫�ȉ^���G�l���M�[�������̂͂���܂���B�d�q�̃G�l���M�[��
���傫�ȉ^���G�l���M�[�������̂͂���܂���B�d�q�̃G�l���M�[��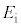 �̏ꍇ�A���o�������d�q�̉^���G�l���M�[
�̏ꍇ�A���o�������d�q�̉^���G�l���M�[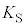 �́A�E�}���
�́A�E�}���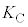 ����
����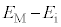 �����������Ȃ�A
�����������Ȃ�A 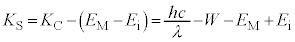 ......[��]
......[��]
��2�@(6)�ŏ������悤�ɁA���o���ꂽ���d�q�̒��ɁA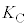 ���傫�ȉ^���G�l���M�[�������d�q�͂���܂���B�����Ȃ��Ă���O���t�͇B ......[��]
���傫�ȉ^���G�l���M�[�������d�q�͂���܂���B�����Ȃ��Ă���O���t�͇B ......[��] �܂��A���A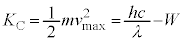 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 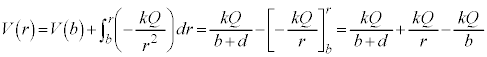
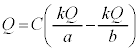 �@��
�@�� 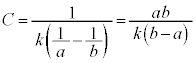 ......[�`]
......[�`]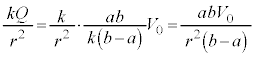 ......[��]
......[��]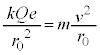 �@��
�@�� 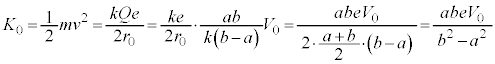 ......[�k]
......[�k]