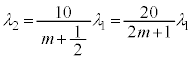���啨��'23�N�O��[3]
���̕��͂�ǂ�ŁA�@�@�@�ɓK�������܂��͐��l���A���ꂼ��̉��ɋL������B�Ȃ��A�@�@�͂��ł��@�@�ŗ^����ꂽ���̂Ɠ������̂�\���B��1�C��2�ł́A�w���ɂ��������āA�����ꂼ��̉��ɋL������B�������A�~������π�Ƃ��A�p�x�̒P�ʂɂ̓��W�A����p����B
�Ό��̓f�B�X�v���[����ʐM�A���ʎq�Z�p�ȂǗl�X�ȕ���ŗ��p����Ă���B���̕Ό��𑀍삷����@�ɂ��čl���Ă݂悤�B
���͓d���g�̈��ł���A�d��Ǝ��ꂪ���̐i�s�����Ɛ����ɐU�����Ȃ���`���B�d��̐U������������A�����ł͕Ό��̕����ƌĂԁB�d��̓x�N�g���ł���A�قȂ�2�̕����̐����ɕ������A�܂��������čl���邱�Ƃ��ł���B�Ό��́A�������̕���(���ߎ��ƌĂ�)�ƕ��s�ɐU������d�ꐬ�����Ȃ����߂��A���ߎ��Ɛ����ɐU������d�ꐬ�������S�ɎՒf����Ƃ���B�܂��ȉ��ōl��������o��̐M�����xI �́A�Ό��̕����Ɉˑ������A���˂�����̓d��̐U����2��ɔ�Ⴗ����̂Ƃ���B
�Ȃ��A�Ό�������o�킨��ь�q���铧�����̂́A���̕\�ʂ����̐i�s�����Ɛ����ɂȂ�悤�ɐ^�ɒu����Ă���A�\�ʂɂ�������̈ʑ��̕ω��┽�˂͖�������B�܂��A�ȉ��ł̓��ˌ��̔g���̒l�͐^�ł̒l�Ƃ���B
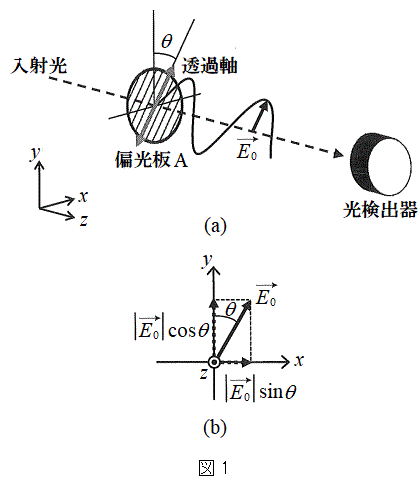 ���܁A�}1(a)�̂悤�ɁA�g����
���܁A�}1(a)�̂悤�ɁA�g����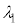 �̒P�F�̓��ˌ����A�Ό���A��ʉ߂�������A�����o��Ō��o�����Bz�������̐i�s�����Ƃ��Đ}1(a)�̍����̂悤��x����y�����Ƃ�A�Ό��̓��ߎ���y���̂Ȃ��p�x��θ�Ƃ���B�Ό���
�̒P�F�̓��ˌ����A�Ό���A��ʉ߂�������A�����o��Ō��o�����Bz�������̐i�s�����Ƃ��Đ}1(a)�̍����̂悤��x����y�����Ƃ�A�Ό��̓��ߎ���y���̂Ȃ��p�x��θ�Ƃ���B�Ό���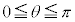 �͈̔͂ŁAxy���ʓ��ʼn�]�ł���B���ˌ��ɂ͂��낢��ȕ����ɐU�����������l�Ɋ܂܂�Ă���B���̂��߁Aθ����L�͈̔͂ŕω��������Ƃ��A�����o��̐M�����x��
�͈̔͂ŁAxy���ʓ��ʼn�]�ł���B���ˌ��ɂ͂��낢��ȕ����ɐU�����������l�Ɋ܂܂�Ă���B���̂��߁Aθ����L�͈̔͂ŕω��������Ƃ��A�����o��̐M�����x��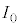 �ŏ�Ɉ��ł������B�܂��A���̔g���̓��ˌ���p�����ꍇ�ɂ����l�̌��ʂ�����ꂽ�B�Ό���A��ʉ߂�����̌��̏�Ԃ́A���̑傫�����d��̐U���ŁA���̌������d��̌����ƈ�v����x�N�g��
�ŏ�Ɉ��ł������B�܂��A���̔g���̓��ˌ���p�����ꍇ�ɂ����l�̌��ʂ�����ꂽ�B�Ό���A��ʉ߂�����̌��̏�Ԃ́A���̑傫�����d��̐U���ŁA���̌������d��̌����ƈ�v����x�N�g��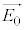 (�ȉ��A�����U���x�N�g���ƌĂ�)��p���ē����Â�����B�}1(b)�Ɏ����悤�ɁA
(�ȉ��A�����U���x�N�g���ƌĂ�)��p���ē����Â�����B�}1(b)�Ɏ����悤�ɁA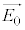 ��x�������̐�����y�������̐����ɕ������čl���邱�Ƃ��ł��A
��x�������̐�����y�������̐����ɕ������čl���邱�Ƃ��ł��A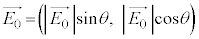 �ƕ\����B�Ȃ��}1(b)�ł͎��ʂ̗�����\�̌�����z���̐��̕����Ƃ���B
�ƕ\����B�Ȃ��}1(b)�ł͎��ʂ̗�����\�̌�����z���̐��̕����Ƃ���B
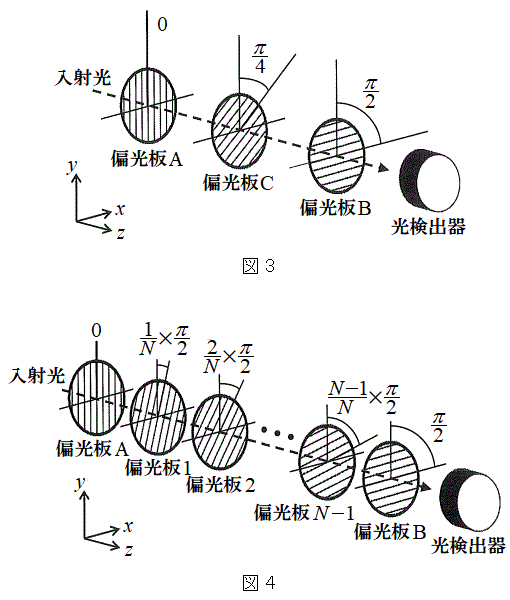 (2) �Ό��̕����𑀍삷����@�Ƃ��āA�Ό��݂̂�p������@�ɂ��čl���悤�B�}3�̂悤�ɁA�Ό���A�̊p�x��0�C�Ό���B�̊p�x��
(2) �Ό��̕����𑀍삷����@�Ƃ��āA�Ό��݂̂�p������@�ɂ��čl���悤�B�}3�̂悤�ɁA�Ό���A�̊p�x��0�C�Ό���B�̊p�x��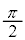 �ɌŒ肵�A���̊ԂɕΌ���C���A�p�x��
�ɌŒ肵�A���̊ԂɕΌ���C���A�p�x��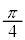 �ɂ��Đݒu�����B�g��
�ɂ��Đݒu�����B�g��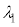 �̌�����˂����Ƃ��̌����o��̐M�����xI �́A�@���@�~
�̌�����˂����Ƃ��̌����o��̐M�����xI �́A�@���@�~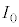 �ł���B
�ł���B���ɐ}4�̂悤�ɁA�Ό���A�̊p�x��0�C�Ό���B�̊p�x��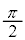 �ɌŒ肵�A���̊ԂɕΌ���
�ɌŒ肵�A���̊ԂɕΌ���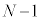 (N��2�ȏ�̐���)���ݒu�����B�Ό���A�ɋ߂����̂��珇�ɕΌ���k (
(N��2�ȏ�̐���)���ݒu�����B�Ό���A�ɋ߂����̂��珇�ɕΌ���k (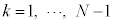 )�ƌĂсA�Ό���k�̊p�x��
)�ƌĂсA�Ό���k�̊p�x��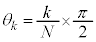 �ɐݒ肷��B�g��
�ɐݒ肷��B�g��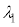 �̌�����˂����Ƃ��̌����o��̐M�����xI �́A�@���@�~
�̌�����˂����Ƃ��̌����o��̐M�����xI �́A�@���@�~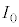 �ł���A
�ł���A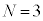 �̂Ƃ��ɂ��@���@�~
�̂Ƃ��ɂ��@���@�~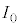 �ƂȂ�B
�ƂȂ�B
�����N��1���\���傫���ꍇ�ɂ��čl���Ă݂悤�B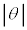 ��1���\��������(
��1���\��������(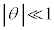 )�Ƃ�
)�Ƃ�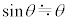 �Ƌߎ��ł��A�܂�a��萔�Ƃ���
�Ƌߎ��ł��A�܂�a��萔�Ƃ���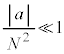 �̂Ƃ�
�̂Ƃ�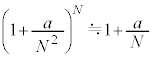 �Ƌߎ��ł��邱�Ƃ�p����ƁA�@���@�~
�Ƌߎ��ł��邱�Ƃ�p����ƁA�@���@�~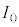 ��
�� �Ƌߎ��ł���B���̂��Ƃ���A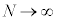 �̋Ɍ��ł̌����o��̐M�����xI �́A
�̋Ɍ��ł̌����o��̐M�����xI �́A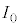 �ɑQ�߂��邱�Ƃ��킩��B���̌��ʂ��A�����x�������������ɕΌ��̕������p�x
�ɑQ�߂��邱�Ƃ��킩��B���̌��ʂ��A�����x�������������ɕΌ��̕������p�x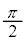 ������]�����邱�Ƃ��A�����I�ɕΌ��݂̂�p���ĉ\�ł���Ƃ����A�����[�����_��������B
������]�����邱�Ƃ��A�����I�ɕΌ��݂̂�p���ĉ\�ł���Ƃ����A�����[�����_��������B
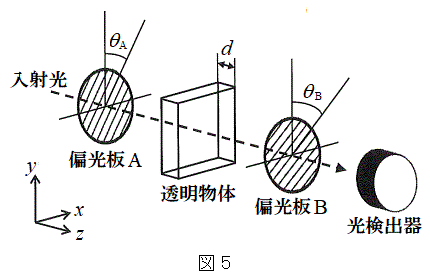 (3) �Ό��̕����𑀍삷��ʂ̕��@�Ƃ��āA���̕Ό��̕����ɂ���ċ��ܗ����قȂ铧���Ȕ}����p������@�ɂ��čl���悤�B�}5�̂悤�ɁA�Ό���A�ƕΌ���B�̊ԂɁA���̂悤�Ȕ}������Ȃ钼���̂̓������̂�}�������ꍇ���l����B���̌��̐i�s�����̌��݂�d�C���̓d��̐U��������x�������̏ꍇ�̋��ܗ���
(3) �Ό��̕����𑀍삷��ʂ̕��@�Ƃ��āA���̕Ό��̕����ɂ���ċ��ܗ����قȂ铧���Ȕ}����p������@�ɂ��čl���悤�B�}5�̂悤�ɁA�Ό���A�ƕΌ���B�̊ԂɁA���̂悤�Ȕ}������Ȃ钼���̂̓������̂�}�������ꍇ���l����B���̌��̐i�s�����̌��݂�d�C���̓d��̐U��������x�������̏ꍇ�̋��ܗ���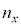 �Cy�������̏ꍇ��
�Cy�������̏ꍇ��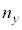 �Ƃ��A�����̋��ܗ��͌��̔g���ɂ�炸���ŁA�݂��ɈقȂ�
�Ƃ��A�����̋��ܗ��͌��̔g���ɂ�炸���ŁA�݂��ɈقȂ�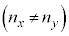 �Ƃ���B�܂��A���̓������̒��ł́A���͕Ό��̕����ɂ�炸�����o�H�i���A���̋z���͖����ł���Ƃ���B
�Ƃ���B�܂��A���̓������̒��ł́A���͕Ό��̕����ɂ�炸�����o�H�i���A���̋z���͖����ł���Ƃ���B���ܕΌ���A�̊p�x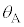 �ƕΌ���B�̊p�x
�ƕΌ���B�̊p�x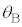 ���Ƃ���
���Ƃ���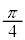 �ɐݒ肵�A�g��
�ɐݒ肵�A�g��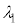 �̌�����˂���ƁA�����o��̐M�����x��0�ɂȂ����B���̂悤�ȏɂȂ铧�����̂̍ŏ��̌��݂����߂Ă݂悤�B
�̌�����˂���ƁA�����o��̐M�����x��0�ɂȂ����B���̂悤�ȏɂȂ铧�����̂̍ŏ��̌��݂����߂Ă݂悤�B
�Ό���A��ʉ߂������̕Ό�������y���ƂȂ��p�x��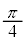 �ł���A�d���x������������y�����������́A���ꂼ��̐U����
�ł���A�d���x������������y�����������́A���ꂼ��̐U����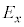 �C
�C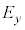 �Ƃ��ē��ʑ�(�ʑ���0)�ŐU�����Ă���B�������̕����̌��H���͓d���x�����������ɑ��Ă��@���@�Cy�����������ɑ��Ă��@���@�ł���A�����̌��H��(
�Ƃ��ē��ʑ�(�ʑ���0)�ŐU�����Ă���B�������̕����̌��H���͓d���x�����������ɑ��Ă��@���@�Cy�����������ɑ��Ă��@���@�ł���A�����̌��H��(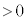 )���@���@�ŗ^������B���̌��H�����A
)���@���@�ŗ^������B���̌��H�����A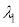 �����0�ȏ�̐���m��p�����@���@�ƕ\�����Ƃ��A�������̂�ʉ߂�����̓d���x������������y�����������͋t�ʑ�(�ʑ���π)�ƂȂ�B���̂Ƃ��A�d��̐U���x�N�g����x�������������A�������̂�ʉ߂���O�ƕς�炸
�����0�ȏ�̐���m��p�����@���@�ƕ\�����Ƃ��A�������̂�ʉ߂�����̓d���x������������y�����������͋t�ʑ�(�ʑ���π)�ƂȂ�B���̂Ƃ��A�d��̐U���x�N�g����x�������������A�������̂�ʉ߂���O�ƕς�炸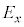 ���Ƃ���Ay�����������́A���������]��
���Ƃ���Ay�����������́A���������]��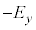 �ƂȂ�B�����̐������x�N�g���Ƃ��č�������錋�ʁA�Ό�������y���ƂȂ��p�x��
�ƂȂ�B�����̐������x�N�g���Ƃ��č�������錋�ʁA�Ό�������y���ƂȂ��p�x��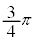 �ƂȂ�A�Ό���B�̓��ߎ��ƒ������A���o��̏o�͂�0�ƂȂ�B���̏��������������̂̍ŏ��̌���
�ƂȂ�A�Ό���B�̓��ߎ��ƒ������A���o��̏o�͂�0�ƂȂ�B���̏��������������̂̍ŏ��̌���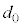 ��
��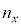 �C
�C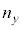 �C
�C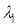 ��p���ĕ\���ƁA
��p���ĕ\���ƁA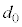 ���@���@�ł���B
���@���@�ł���B
��1�@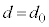 �̂Ƃ��A�Ό���A�ƕΌ���B�̊p�x���Ƃ���θ�Ƃ��āAθ��0����
�̂Ƃ��A�Ό���A�ƕΌ���B�̊p�x���Ƃ���θ�Ƃ��āAθ��0����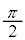 �܂ŕω��������ۂ̌����o��̐M�����xI �̕ω����A�O���t�ɕ`���B���̍ہAθ�������A�����o��̐M�����xI ���c���ɂƂ�A�M�����xI �̍ő�l�A�ŏ��l�ƁA���ꂼ��ɑΉ�����θ�̒l��������悤�ɐ}������B
�܂ŕω��������ۂ̌����o��̐M�����xI �̕ω����A�O���t�ɕ`���B���̍ہAθ�������A�����o��̐M�����xI ���c���ɂƂ�A�M�����xI �̍ő�l�A�ŏ��l�ƁA���ꂼ��ɑΉ�����θ�̒l��������悤�ɐ}������B
(4) (3)�̏ŁA�}5�̕Ό���A�̊p�x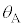 �ƕΌ���B�̊p�x
�ƕΌ���B�̊p�x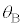 ���Ƃ���
���Ƃ���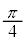 �ɐݒ肵�A����ǂ͌��݂�
�ɐݒ肵�A����ǂ͌��݂�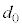 ��20�{(
��20�{(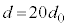 )�̓���̓������̂�ݒu���āA�g��
)�̓���̓������̂�ݒu���āA�g��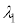 �̌�����˂����B���̂Ƃ��A�����o��̐M�����x���@���@�~
�̌�����˂����B���̂Ƃ��A�����o��̐M�����x���@���@�~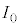 �ƂȂ����B
�ƂȂ����B
��2�@(4)�̏ŁA���ˌ��Ƃ��Ĕg����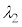 �̒P�F�̌���p����ƁA�M�����x��0�ƂȂ����B���̂悤�ȓ��ˌ��̔g��
�̒P�F�̌���p����ƁA�M�����x��0�ƂȂ����B���̂悤�ȓ��ˌ��̔g��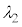 �͕����l������B
�͕����l������B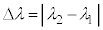 �Ƃ��āA�ŏ���
�Ƃ��āA�ŏ���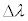 ���A
���A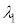 ��p���ĕ\���B���o�ߒ��������B
��p���ĕ\���B���o�ߒ��������B
�ȏ�Œ��ׂ��A���ܗ����قȂ镨���ɂ�����Ό������̕ω��́A�����̐�������ׂ݂�Ό��������Ȃǂł����p����Ă���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�u�Ό��v�Ȃǂƌ�����Ƌ��|��������܂����A�e�ȗU���ɏ���ĉ�i�߂čs���܂��B�Ōゾ���l�����ނ����m��܂���B
�܂��A��蕶���́u�O�y�[�W�̉������v�́A�������q�ł̂��ƂȂ̂ŁA���̃E�F�u�y�[�W�ɂ����ẮA�u��L�̉������v�Ɠǂނ悤�ɂ��Ă��������B
�����o��̐M�����x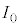 �́A���o��ɓ��˂�������d���̐U��
�́A���o��ɓ��˂�������d���̐U��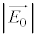 ��2��ɔ�Ⴕ�A�}1(a)�ŕΌ���A�ɓ��˂�����ɂ͂��낢��ȕ����ɐU�����������l�Ɋ܂܂�Ă���̂ŁA�Ό��̓��ߎ���y���Ƃ̊pθ�������Ȃ�p�ł����Ă��Ak����萔�Ƃ��āA
��2��ɔ�Ⴕ�A�}1(a)�ŕΌ���A�ɓ��˂�����ɂ͂��낢��ȕ����ɐU�����������l�Ɋ܂܂�Ă���̂ŁA�Ό��̓��ߎ���y���Ƃ̊pθ�������Ȃ�p�ł����Ă��Ak����萔�Ƃ��āA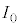 �́A
�́A
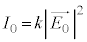 �@����@
�@����@
�ɂȂ�Ƃ��čl���܂�(���啨��23�N[2](2)�̒����Q��)�B���̂Ƃ��A���ߌ���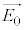 �͕Ό��̓��ߕ����������Ă��邱�Ƃɂ����ӂ��Ă��������B
�͕Ό��̓��ߕ����������Ă��邱�Ƃɂ����ӂ��Ă��������B
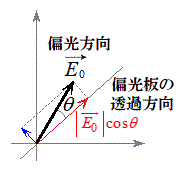 �܂��}1(b)����A
�܂��}1(b)����A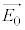 �̕Ό������̌�������Ɗpθ���Ȃ������ߕ����Ƃ���Ό���ʉ߂�����̐U���́A
�̕Ό������̌�������Ɗpθ���Ȃ������ߕ����Ƃ���Ό���ʉ߂�����̐U���́A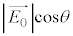 �ƂȂ邱�Ƃ��킩��܂�(�E�})�B
�ƂȂ邱�Ƃ��킩��܂�(�E�})�B
���D��蕶�̐����ɂ��ƁA�U���x�N�g���𐬕��ɕ����čl����ƁA�݂��ɐ����ȓ��ߕ�����L����2���̕Ό��߂��Ă��܂���������悤�ȍ��o���N���邩���m��܂���B����������ɐU�����������l�Ɋ܂ޓ��ˌ����Ay�����玞�v���Ɋpθ������]���������ߎ������Ό��ɓ��˂��Ēʉ߂�����ƁA�}1(b)�̕���(�Ό��̓��ߎ��̌���)�������U���x�N�g��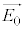 �C
�C �ƂȂ�킯�ł����A���̓��ߌ�������ɁAy�����玞�v���Ɋp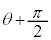 ������]���������ߎ������Ό��ɓ��˂������Ƃ��܂��B
������]���������ߎ������Ό��ɓ��˂������Ƃ��܂��B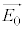 ��x��������
��x��������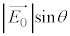 �̓��ߎ�����������
�̓��ߎ�����������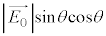 �ŁA����Ɛ����ȕ���(
�ŁA����Ɛ����ȕ���(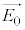 ����)�����͎Ւf����܂��B
����)�����͎Ւf����܂��B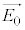 ��y��������
��y��������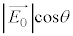 �̓��ߎ�����������
�̓��ߎ����������� �ŁA����Ɛ����ȕ��������͎Ւf����܂��B���ߌ��̐U���x�N�g�����Ay�����玞�v���Ɋp
�ŁA����Ɛ����ȕ��������͎Ւf����܂��B���ߌ��̐U���x�N�g�����Ay�����玞�v���Ɋp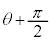 ������]�������������悤�Ɏv���܂����A���ߎ����������́A
������]�������������悤�Ɏv���܂����A���ߎ����������́A �ƂȂ�̂ŁA�����ɕ����čl���Ă��A���ߕ�����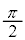 �����قȂ�2���̕Ό���ʂ��ƁA���S�ɎՒf����邱�ƂɂȂ�܂��B
�����قȂ�2���̕Ό���ʂ��ƁA���S�ɎՒf����邱�ƂɂȂ�܂��B
(1) �}2�ɂ����āA�Ό���B�̓��ߕ����͕Ό���A�̓��ߕ����Ɗp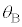 ���Ȃ��̂ŁA�Ό���B��ʉ߂�����̐U���x�N�g���̓��ߕ���������
���Ȃ��̂ŁA�Ό���B��ʉ߂�����̐U���x�N�g���̓��ߕ���������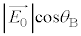 �ł��B�����o��̐M�����x�́A�@���A
�ł��B�����o��̐M�����x�́A�@���A 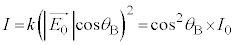 �@
�@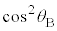 ......[��]
......[��]�Ό���B�̓��ߕ����ƕΌ���A�̓��ߕ�������v����Ƃ��́A�Ό���B��ʉ߂�����̓��ߕ����̐U����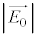 �ł��B�����o��̐M�����x�́A�@���A
�ł��B�����o��̐M�����x�́A�@���A 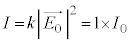 �@1 ......[��]
�@1 ......[��]
(2) �}3�ɂ����āA�Ό���C�̓��ߕ����͕Ό���A�̓��ߕ����Ɗp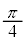 ���Ȃ��A�Ό���B�̓��ߕ����͕Ό���C�̓��ߕ����Ɗp
���Ȃ��A�Ό���B�̓��ߕ����͕Ό���C�̓��ߕ����Ɗp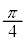 ���Ȃ��̂ŁA�Ό���B��ʉ߂�����̐U���x�N�g���̓��ߕ���������
���Ȃ��̂ŁA�Ό���B��ʉ߂�����̐U���x�N�g���̓��ߕ���������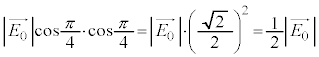 �ł��B�����o��̐M�����x�́A�@���A
�ł��B�����o��̐M�����x�́A�@���A 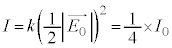 �@
�@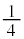 ......[��]
......[��]�܂�A�Ό���A�ƕΌ���B�̓��ߕ������݂��ɐ����ł����Ă��AA��B�̊Ԃɒ��ԓI�ȕΌ�������L����Ό������ނƁA���߂�������ł���A�Ƃ����킯�ł��B
�}4�ɂ����āA�Ό���1�ʉ߂��邲�Ƃɂ��̓��ߕ������A1��O�̕Ό��̓��ߕ����ƂȂ��p��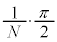 �Ȃ̂ŁA�Ό���1�ʉ߂��邲�ƂɁA�U���x�N�g���̓��ߕ���������
�Ȃ̂ŁA�Ό���1�ʉ߂��邲�ƂɁA�U���x�N�g���̓��ߕ���������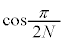 �{����Ă����܂��B�S����N���̕Ό���ʉ߂���̂ŁA�U���x�N�g���̓��ߕ���������
�{����Ă����܂��B�S����N���̕Ό���ʉ߂���̂ŁA�U���x�N�g���̓��ߕ���������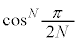 �{����܂��B�����o��̐M�����x�́A
�{����܂��B�����o��̐M�����x�́A 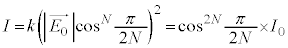 �@
�@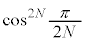 ......[��]
......[��][��]�̌��ʂ�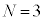 �Ƃ���ƁA
�Ƃ���ƁA 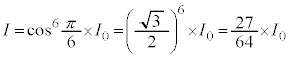 �@
�@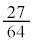 ......[��]
......[��]N���\���傫���ꍇ�A��蕶�̋ߎ������A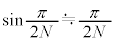 �C[��]�̌��ʂɂ��āA
�C[��]�̌��ʂɂ��āA �����ŁA��蕶�̋ߎ�����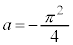 �Ƃ݂āA�����o��̐M�����x�́A
�Ƃ݂āA�����o��̐M�����x�́A 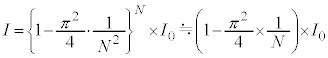 �@
�@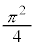 ......[��]
......[��]
(3) �g��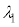 �̌��́A���ܗ�
�̌��́A���ܗ�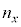 �̕������ł͔g����
�̕������ł͔g����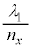 �ɂȂ�A���ܗ�
�ɂȂ�A���ܗ�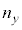 �̕������ł͔g����
�̕������ł͔g����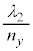 �ɂȂ�A�Ό������ɂ���Ĕg�����قȂ邱�ƂɂȂ�܂��B���̖��ł͂�����A�g��
�ɂȂ�A�Ό������ɂ���Ĕg�����قȂ邱�ƂɂȂ�܂��B���̖��ł͂�����A�g��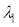 �̂܂ܓ������̒���i�݁A���������ܗ��{�������H����ʉ߂���ƍl����̂ŁA��������d�i�ނƂ��A�d���x�����������ɑ��Ă͌��H��
�̂܂ܓ������̒���i�݁A���������ܗ��{�������H����ʉ߂���ƍl����̂ŁA��������d�i�ނƂ��A�d���x�����������ɑ��Ă͌��H��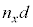 �Cy�����������ɑ��Ă͌��H��
�Cy�����������ɑ��Ă͌��H��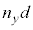 �����i�ނƍl���܂��B�@
�����i�ނƍl���܂��B�@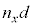 ......[��]�@
......[��]�@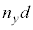 ......[��]
......[��] �����̌��H��(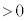 )�́A
)�́A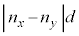 ......[��]�������̂������ʉ߂�����ɓd���x������������y�������������t�ʑ��ɂȂ�(�g�̈ʑ����Q��)�̂́A���H�������g���̊�{�ɂȂ�(�g�̊������Q��)�Ƃ��ŁAm��0�ȏ�̐����Ƃ��āA
......[��]�������̂������ʉ߂�����ɓd���x������������y�������������t�ʑ��ɂȂ�(�g�̈ʑ����Q��)�̂́A���H�������g���̊�{�ɂȂ�(�g�̊������Q��)�Ƃ��ŁAm��0�ȏ�̐����Ƃ��āA 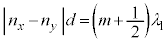 �@����A
�@����A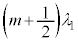 ......[��]�ƂȂ�܂��B
......[��]�ƂȂ�܂��B
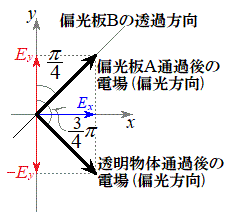 ��蕶�ɁA�������̂ɐi���O�ɕΌ�������y���ƂȂ��p��
��蕶�ɁA�������̂ɐi���O�ɕΌ�������y���ƂȂ��p��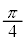 �ł��������̂��A�������̒ʉߌ��y�����������������]����
�ł��������̂��A�������̒ʉߌ��y�����������������]����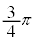 �ɂȂ邱�Ƃ���������Ă��܂����A���̏��E�}�Ɏ����܂��B
�ɂȂ邱�Ƃ���������Ă��܂����A���̏��E�}�Ɏ����܂��B
�A�ɂ����āA���o��̏o�͂�0�ɂȂ���������ŏ���d�́A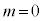 �̂Ƃ��ŁA���̂Ƃ��̓������̂̌���
�̂Ƃ��ŁA���̂Ƃ��̓������̂̌���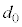 �́A
�́A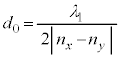 ......[��]�@����B
......[��]�@����B
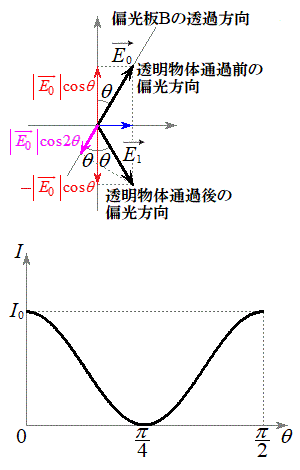 ��1�@�Ό���A�ƕΌ���B�̊p���Ƃ���θ�Ƃ���ƁA�Ό���A�ʉߌ�̓d��͖�蕶�̐}1(b)�̂悤�ɂȂ�܂��B
��1�@�Ό���A�ƕΌ���B�̊p���Ƃ���θ�Ƃ���ƁA�Ό���A�ʉߌ�̓d��͖�蕶�̐}1(b)�̂悤�ɂȂ�܂��B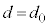 �̂Ƃ��A��蕶�ɏ�����Ă���悤�ɁA�������̒ʉߌ�A�d��̐U���x�N�g����y���������������]���܂��B�d��̐U���x�N�g����
�̂Ƃ��A��蕶�ɏ�����Ă���悤�ɁA�������̒ʉߌ�A�d��̐U���x�N�g����y���������������]���܂��B�d��̐U���x�N�g����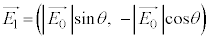 �ƂȂ�܂����A���ꂪy���Ɗpθ���Ȃ��Ό���B��ʉ߂���ƁA�E��}�̂悤�ɁA
�ƂȂ�܂����A���ꂪy���Ɗpθ���Ȃ��Ό���B��ʉ߂���ƁA�E��}�̂悤�ɁA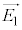 �ƕΌ���B�̓��ߕ����͊p
�ƕΌ���B�̓��ߕ����͊p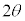 ���Ȃ��̂ŁA�Ό���B���ߕ���������
���Ȃ��̂ŁA�Ό���B���ߕ���������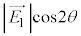 �ƂȂ�A���ꂪ�U���ɂȂ�̂ŁA�����o��̐M�����x�́A
�ƂȂ�A���ꂪ�U���ɂȂ�̂ŁA�����o��̐M�����x�́A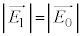 �ɒ��ӂ��āA
�ɒ��ӂ��āA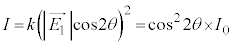 �@����C
�@����C�C�ɂ��ƁA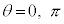 �̂Ƃ�
�̂Ƃ� (�ő�l)�C
(�ő�l)�C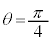 �̂Ƃ�
�̂Ƃ�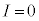 (�ŏ��l)�ƂȂ�̂ŁA�M�����x�̕ω��̃O���t�͉E���}�B
(�ŏ��l)�ƂȂ�̂ŁA�M�����x�̕ω��̃O���t�͉E���}�B
(4) 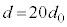 �̂Ƃ��̌��H���́A�B���A
�̂Ƃ��̌��H���́A�B���A ���H�����A�g���̐����{�Ȃ̂ŁA�d���x������������y�����������͓��ʑ��ł��B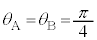 �Ȃ̂ŁA(1)[��]�Ɠ����ɂȂ�A�����o��̐M�����x�́A
�Ȃ̂ŁA(1)[��]�Ɠ����ɂȂ�A�����o��̐M�����x�́A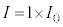 �@1 ......[��]
�@1 ......[��]
��2�@�g��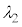 �̂Ƃ��A�����o��̐M�����x��0�������A�Ƃ������Ƃ́A�������̒ʉߌ�̓d���x������������y�����������͋t�ʑ��������Ƃ������ƂŁA�A��
�̂Ƃ��A�����o��̐M�����x��0�������A�Ƃ������Ƃ́A�������̒ʉߌ�̓d���x������������y�����������͋t�ʑ��������Ƃ������ƂŁA�A��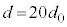 �ƍl���Am��0�ȏ�̐����Ƃ��āA
�ƍl���Am��0�ȏ�̐����Ƃ��āA 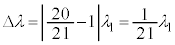 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 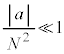 �̂Ƃ�
�̂Ƃ�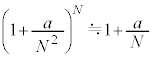 �Ƌߎ��ł��邱�Ƃ�p����ƁA�@���@�~
�Ƌߎ��ł��邱�Ƃ�p����ƁA�@���@�~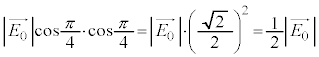 �ł��B�����o��̐M�����x�́A�@���A
�ł��B�����o��̐M�����x�́A�@���A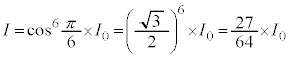 �@
�@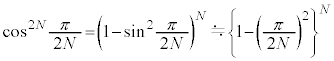
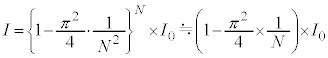 �@
�@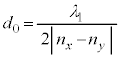 ......[��]�@����B
......[��]�@����B