東大物理'23年前期[2]
質量を精密に測定する装置について考えよう。
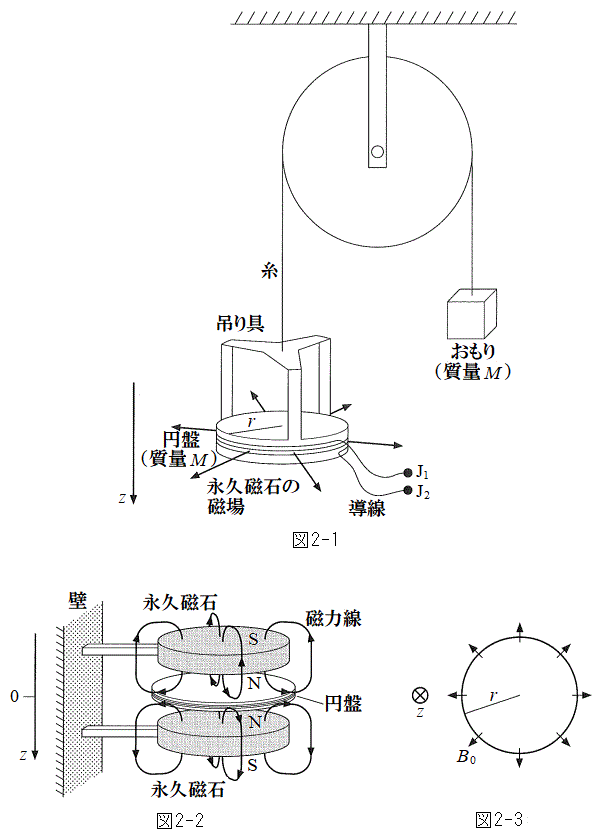 Ⅰ 図2-1のように、滑らかに回転する軽い滑車に、半径r,質量Mの円盤が、質量の無視できる糸と吊り具で水平につり下げられている。円盤の側面には導線が水平方向にN回巻かれている。導線の巻き方向は、上から見たときに端子
Ⅰ 図2-1のように、滑らかに回転する軽い滑車に、半径r,質量Mの円盤が、質量の無視できる糸と吊り具で水平につり下げられている。円盤の側面には導線が水平方向にN回巻かれている。導線の巻き方向は、上から見たときに端子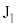 を始点として時計回りである。滑車の反対側には質量Mのおもりがつり下げられている。円盤の厚さは十分に小さいものとする。
を始点として時計回りである。滑車の反対側には質量Mのおもりがつり下げられている。円盤の厚さは十分に小さいものとする。円盤の上下には図2-2のように、二つの円形の永久磁石をN極同士が向かい合うように壁に固定する。鉛直方向下向きにz軸をとり、二つの磁石の中間点を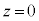 とする。円盤は、はじめ
とする。円盤は、はじめ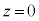 に配置されており、水平を保ちながらz方向にのみ運動する。円盤が動く範囲では、図2-3のように円盤の半径方向を向いた放射状の磁場が永久磁石により作られ、導線の位置での磁束密度の大きさは一定の値
に配置されており、水平を保ちながらz方向にのみ運動する。円盤が動く範囲では、図2-3のように円盤の半径方向を向いた放射状の磁場が永久磁石により作られ、導線の位置での磁束密度の大きさは一定の値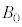 である。この磁場は円盤に巻かれた導線のみに作用するものとする。
である。この磁場は円盤に巻かれた導線のみに作用するものとする。
この装置は真空中に置かれている。重力加速度は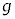 ,真空中の光速はcとする。円盤が動く速さはcよりも十分に小さい。糸の伸縮はない。導線の質量、太さ、抵抗、自己インダクタンスは無視する。また、円盤に巻かれていない部分の導線は、円盤の運動に影響しない。以下の設問に答えよ。
,真空中の光速はcとする。円盤が動く速さはcよりも十分に小さい。糸の伸縮はない。導線の質量、太さ、抵抗、自己インダクタンスは無視する。また、円盤に巻かれていない部分の導線は、円盤の運動に影響しない。以下の設問に答えよ。
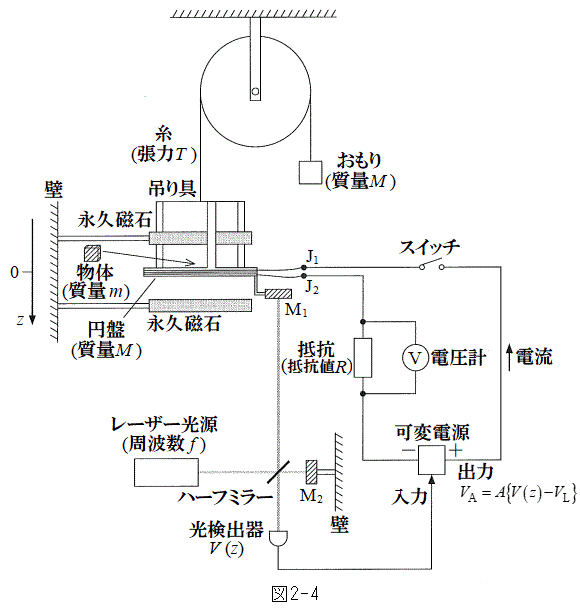 図2-4のように、円盤の位置を精密に測定し電気信号に変換するため、この装置にはレーザー干渉計が組み込まれている。レーザー光源を出た周波数f の光は、ハーフミラーで一部が反射し、一部は透過する。ハーフミラーで反射した光は円盤に取り付けた鏡
図2-4のように、円盤の位置を精密に測定し電気信号に変換するため、この装置にはレーザー干渉計が組み込まれている。レーザー光源を出た周波数f の光は、ハーフミラーで一部が反射し、一部は透過する。ハーフミラーで反射した光は円盤に取り付けた鏡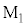 で反射し、ハーフミラーを透過した光は壁に固定された鏡
で反射し、ハーフミラーを透過した光は壁に固定された鏡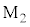 で反射する。
で反射する。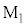 ,
,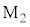 で反射した光は、ハーフミラーで重ね合わされ光検出器に向かう。光の経路は真空中にある。このとき、円盤の位置zが変化すると、検出される光の強さが干渉により変化する。光検出器からは、検出した光の強さに比例した電圧
で反射した光は、ハーフミラーで重ね合わされ光検出器に向かう。光の経路は真空中にある。このとき、円盤の位置zが変化すると、検出される光の強さが干渉により変化する。光検出器からは、検出した光の強さに比例した電圧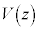 が出力される。この電圧は、
が出力される。この電圧は、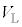 とkを正の定数として
とkを正の定数として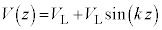 と表すことができる。鏡
と表すことができる。鏡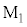 の質量は無視できる。
の質量は無視できる。
(2) f とcを用いてkを表せ。
図2-4の回路に含まれる可変電源は、光検出器の出力電圧を入力すると、正の増幅率をAとして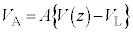 なる電圧を出力する。抵抗値Rの抵抗に生じる電圧降下を、内部抵抗の十分大きな電圧計によって測定する。
なる電圧を出力する。抵抗値Rの抵抗に生じる電圧降下を、内部抵抗の十分大きな電圧計によって測定する。
いま、円盤の位置を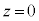 に戻し、静止させた。スイッチを閉じると円盤は静止を続けた。次に、円盤の上に質量mの物体を静かに置くと、物体と円盤は一体となって鉛直下向きに運動を始めた。
に戻し、静止させた。スイッチを閉じると円盤は静止を続けた。次に、円盤の上に質量mの物体を静かに置くと、物体と円盤は一体となって鉛直下向きに運動を始めた。
(3) 円盤をつり下げている糸の張力をT,物体の速度をvとする。一体となって運動する物体と円盤にはたらく力の合力を、k,m,M,T,A,r,N,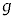 ,
,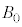 ,R,
,R,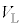 ,v,zのうち必要なものを用いて表せ。
,v,zのうち必要なものを用いて表せ。 Aが十分大きい値であったため、物体と円盤は一体のまま非常に小さな振幅で上下に運動し、時間とともにその振幅は減衰した。時間が経過してほぼ静止したと見なせるときの円盤の位置を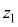 ,電圧計の測定値の絶対値を
,電圧計の測定値の絶対値を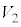 とする。
とする。
(4) 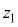 と
と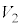 をk,m,A,r,N,
をk,m,A,r,N,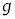 ,
,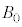 ,R,
,R,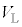 のうち必要なものを用いて表せ。ただし、
のうち必要なものを用いて表せ。ただし、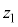 が十分に小さいため、近似式
が十分に小さいため、近似式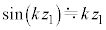 を用いてもよい。
を用いてもよい。
Ⅱ 質量mの測定に用いた抵抗の抵抗値Rを精密に決めることを考えよう。
金属や半導体に電流を流し、その電流の向きと垂直に磁場をかけると、ホール効果によって電流と磁場に垂直な方向に電位差が生じる。このような電子部品をホール素子と呼ぶ。ホール効果のうち、量子ホール効果という特殊な場合には、生じた電位差と電流の比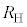 の値は厳密に決まっており、抵抗値の基準となる。
の値は厳密に決まっており、抵抗値の基準となる。
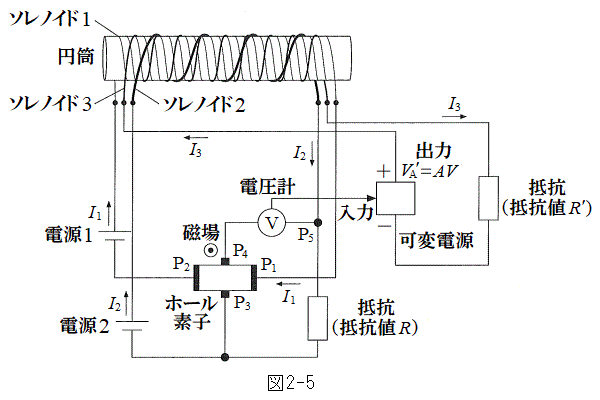
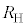 を基準として未知の抵抗値Rを測定するため、図2-5に示す回路を用いる。ホール素子には、紙面に垂直で裏から表に向かう磁場がかけられており、
を基準として未知の抵抗値Rを測定するため、図2-5に示す回路を用いる。ホール素子には、紙面に垂直で裏から表に向かう磁場がかけられており、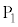 から
から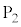 の向きに電流
の向きに電流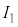 を流すと、
を流すと、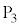 を基準とした
を基準とした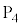 の電位は
の電位は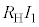 となる。
となる。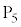 を基準とした
を基準とした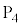 の電位Vを内部抵抗の十分大きな電圧計で測定し、正の大きな増幅率Aをもつ可変電源に入力する。可変電源は電圧
の電位Vを内部抵抗の十分大きな電圧計で測定し、正の大きな増幅率Aをもつ可変電源に入力する。可変電源は電圧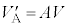 を出力し、抵抗値
を出力し、抵抗値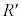 の抵抗に接続されている。ホール素子は、
の抵抗に接続されている。ホール素子は、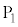 と
と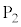 の間に有限の抵抗値をもつ。
の間に有限の抵抗値をもつ。
ソレノイド1,2,3は比透磁率1の一つの円筒に巻かれており、単位長さあたりの巻数はそれぞれ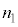 ,
,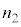 ,
,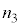 である。ソレノイド2と3は同じ向きに、ソレノイド1はそれらとは逆向きに巻かれている。電源1,電源2,可変電源から流れる電流をそれぞれ
である。ソレノイド2と3は同じ向きに、ソレノイド1はそれらとは逆向きに巻かれている。電源1,電源2,可変電源から流れる電流をそれぞれ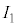 ,
,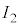 ,
,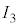 とし、それぞれがソレノイド1,2,3に流れている。
とし、それぞれがソレノイド1,2,3に流れている。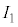 と
と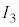 は電源に内蔵された電流計で測定している。ソレノイドの導線の抵抗は無視できる。以下の設問に答えよ。
は電源に内蔵された電流計で測定している。ソレノイドの導線の抵抗は無視できる。以下の設問に答えよ。
(1) 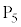 を基準とした
を基準とした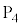 の電位Vとソレノイド内部の磁場Hの大きさを、
の電位Vとソレノイド内部の磁場Hの大きさを、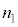 ,
,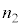 ,
,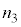 ,
,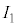 ,
,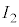 ,
,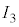 ,R,
,R,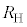 のうち必要なものを用いてそれぞれ表せ。
のうち必要なものを用いてそれぞれ表せ。
(2) 以下の記述について、 と
と にあてはまる式を、
にあてはまる式を、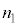 ,
,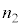 ,
,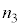 ,
,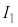 ,
,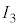 ,R,
,R,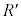 のうち必要なものを用いて表せ。
のうち必要なものを用いて表せ。 磁気センサーでソレノイド内部の磁場Hを測定し、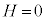 となるように電源1の電圧により
となるように電源1の電圧により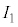 を調整した。このとき、
を調整した。このとき、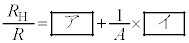 と表すことができる。増幅率Aが大きいので、近似式
と表すことができる。増幅率Aが大きいので、近似式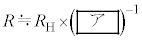 が得られる。
が得られる。 ソレノイドの巻数をうまく選ぶことで、電流の測定誤差に比べて抵抗値Rの測定誤差を相対的に小さくすることができる。量子ホール効果での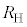 は、物理定数であるプランク定数h,電気素量eと自然数pを用いて
は、物理定数であるプランク定数h,電気素量eと自然数pを用いて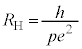 と表せる。ここでは、
と表せる。ここでは、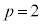 ,
,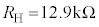 の素子を用いる。いま、測定したい抵抗値Rは
の素子を用いる。いま、測定したい抵抗値Rは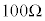 程度であることが測定前にわかっている。測定誤差を小さくするために、
程度であることが測定前にわかっている。測定誤差を小さくするために、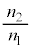 が
が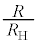 と近い値となり、
と近い値となり、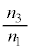 が小さくなるように巻数の比を選び、
が小さくなるように巻数の比を選び、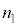 :
: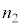 :
: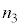 = 1290:10:129とした。
= 1290:10:129とした。
(3) 電流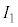 と
と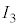 の測定値と真の値、および抵抗値Rの真の値を表2-1に示す。電流の相対誤差は10%程度である。
の測定値と真の値、および抵抗値Rの真の値を表2-1に示す。電流の相対誤差は10%程度である。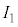 ,
,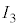 の測定値と設問Ⅱ(2)で得た近似式から、抵抗値Rの測定値を有効数字3桁で求めよ。また、この抵抗測定の相対誤差は何%か、有効数字1桁で答えよ。
の測定値と設問Ⅱ(2)で得た近似式から、抵抗値Rの測定値を有効数字3桁で求めよ。また、この抵抗測定の相対誤差は何%か、有効数字1桁で答えよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 実験装置は大がかりで内容も広範に渡り、我を失いそうですが、そういうときこそ基本に忠実に取り組むべきです。
Ⅰ(1) 電流経路は円形ですが、円周の各一部分について、フレミング右手の法則より、生じる起電力の向きは時計回り方向(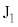 から
から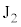 に電流が流れる向き)で、
に電流が流れる向き)で、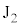 が
が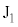 よりも高電位になります。
よりも高電位になります。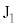 を基準とした
を基準とした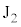 の電位
の電位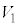 は、磁場中を電流が流れる部分の長さが円周の長さ
は、磁場中を電流が流れる部分の長さが円周の長さ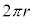 のN倍になることから、
のN倍になることから、 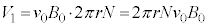 ......[答] ・・・①
......[答] ・・・①
(2) 光波の強さは波動の振動数の2倍の振動数で変化するので、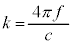 ......[答]
......[答] 注.問題文中に書かれている、光の強さに比例した電圧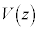 の式ですが、「波の強さ」は、波の進む向きに垂直な単位面積を単位時間に通過する波のエネルギー、として定義されます。
の式ですが、「波の強さ」は、波の進む向きに垂直な単位面積を単位時間に通過する波のエネルギー、として定義されます。 波の振動数をf ,位相のずれをδ,Kを定数として、波のエネルギーは、単振動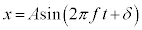 について、単振動の位置エネルギーとして、
について、単振動の位置エネルギーとして、 のように考えます(バネの弾性エネルギーのように考えます。バネ振り子を参照)。
ここで考えている光波の強さは、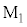 で反射して戻ってくる光と
で反射して戻ってくる光と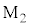 で反射して戻ってくる光との干渉光の強さなのですが、干渉の影響(波の干渉を参照)を考察してみます。
で反射して戻ってくる光との干渉光の強さなのですが、干渉の影響(波の干渉を参照)を考察してみます。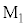 で反射して戻ってくる光の波動の式を、ハーフミラーと
で反射して戻ってくる光の波動の式を、ハーフミラーと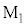 との最初の距離を
との最初の距離を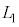 として、
として、 とします。ここで、円盤のz座標は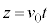 です。
です。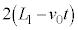 は光が往復する距離です。
は光が往復する距離です。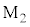 で反射して戻ってくる光の波動の式を、ハーフミラーと
で反射して戻ってくる光の波動の式を、ハーフミラーと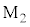 との距離を
との距離を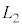 として、
として、 とします。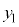 と
と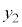 が干渉すると、
が干渉すると、 sinの方は振動数f の振動(干渉しても光波の振動数自体はほぼ変化しません)を表し、zによる干渉の影響はcosの方が表します。cosの方は、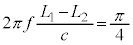 となるように光波の位相(
となるように光波の位相(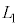 ,
,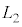 )を調整すると、前述のように干渉光の強さは、変位の2乗に比例するので、
)を調整すると、前述のように干渉光の強さは、変位の2乗に比例するので、 に比例し、問題文にあるように、
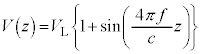 ・・・②
・・・②となります。
円盤が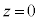 の位置で静止しているときに円盤に働く力は上向きの張力T,円盤に働く下向きの重力
の位置で静止しているときに円盤に働く力は上向きの張力T,円盤に働く下向きの重力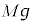 で、このつり合いより、
で、このつり合いより、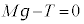 ・・・③
・・・③
(3) 一体となって運動しているとき、物体と円盤に働く力を考えます。まず、上向きの張力T,下向きの重力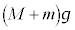 ,また、②より、可変電源の電圧
,また、②より、可変電源の電圧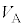 は、
は、 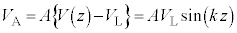 ・・・④
・・・④なので、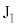 から
から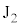 に向って円盤に巻かれた長さ
に向って円盤に巻かれた長さ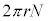 の導線に流れる電流は、可変電源の電圧
の導線に流れる電流は、可変電源の電圧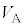 と、円盤に巻かれた導線に生ずるⅠ(1)の起電力
と、円盤に巻かれた導線に生ずるⅠ(1)の起電力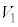 (ここでは円盤の速さは
(ここでは円盤の速さは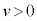 )を合わせて、オームの法則より、
)を合わせて、オームの法則より、 以上より、運動する物体と円盤に働く力の合力は、
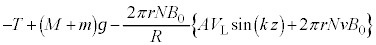 ......[答]
......[答]
(4) 時間が経過して静止したと見なせるときにも③が成立し(3)の結果で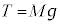 とし、また、
とし、また、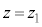 ,
,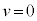 とすると、(3)の合力は、
とすると、(3)の合力は、 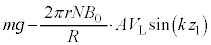 ・・・⑤
・・・⑤となります。また、⑤の合力は力のつり合いより0です。
④で、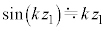 より、
より、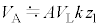 ,電圧計の測定値の絶対値は
,電圧計の測定値の絶対値は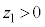 より
より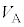 に等しく(この時点で円盤に巻かれている導線の起電力は0)、
に等しく(この時点で円盤に巻かれている導線の起電力は0)、 これらより、
(5) ①より、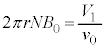 ,これと⑥より、
,これと⑥より、 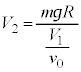 ∴
∴ 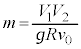 ......[答]
......[答]
Ⅱ(1) 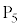 から
から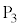 までの抵抗の電圧降下は
までの抵抗の電圧降下は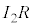 ,ホール素子内で電流
,ホール素子内で電流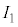 は磁場により上向き(
は磁場により上向き(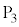 から
から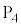 の向き、フレミング左手の法則を参照)に力を受け
の向き、フレミング左手の法則を参照)に力を受け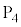 側に正電荷が引き寄せられ、
側に正電荷が引き寄せられ、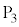 より
より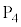 の方が電位が高く、
の方が電位が高く、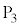 ,
,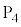 間の電位差は問題文より
間の電位差は問題文より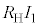 で、
で、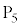 を基準とした
を基準とした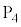 の電位Vは、
の電位Vは、 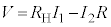 ......[答] ・・・⑦
......[答] ・・・⑦ソレノイド1に図2-5の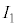 の矢印の方向に電流
の矢印の方向に電流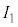 を流すとソレノイド1の内部には、右ねじの法則より、左から右に向かう向きの磁場ができます。ソレノイド2とソレノイド3は、図2-5の
を流すとソレノイド1の内部には、右ねじの法則より、左から右に向かう向きの磁場ができます。ソレノイド2とソレノイド3は、図2-5の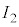 ,
,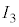 の向きに電流を流すと、内部には、右から左に向かう向きの磁場ができます。ソレノイド内部の磁場Hの大きさ
の向きに電流を流すと、内部には、右から左に向かう向きの磁場ができます。ソレノイド内部の磁場Hの大きさ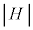 は(電流の作る磁界を参照)、それぞれの磁場の大小関係が不明なため絶対値をつけて、
は(電流の作る磁界を参照)、それぞれの磁場の大小関係が不明なため絶対値をつけて、 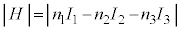 ......[答] ・・・⑧
......[答] ・・・⑧
(2) ⑧で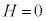 となるように電流
となるように電流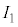 を調整するので、
を調整するので、 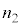 で割り、
で割り、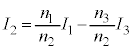 ・・・⑨
・・・⑨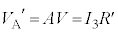 ・・・⑩
・・・⑩⑩に⑦を代入して、
両辺を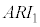 で割ると、
で割ると、 ⑨より、
Aが充分に大きければ、
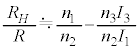 ,
,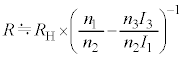 ・・・⑪
・・・⑪となります。
(3) ⑪に、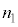 :
: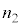 :
: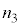 = 1290:10:129,及び、表2-1の測定値を代入すると、
= 1290:10:129,及び、表2-1の測定値を代入すると、 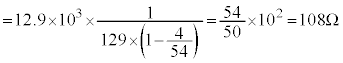 ......[答]
......[答]相対誤差は、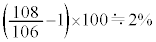 ......[答]
......[答] 注.問題文に、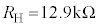 と書かれているので、有効数字3桁での解答を、
と書かれているので、有効数字3桁での解答を、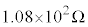 とするよりも、
とするよりも、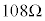 とする方がよいと思います。
とする方がよいと思います。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大物理TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 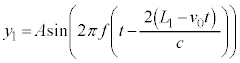
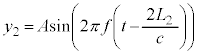
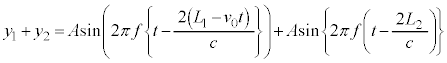
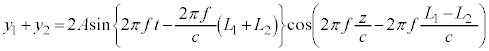
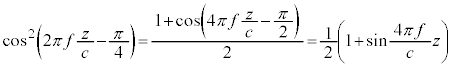
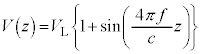 ・・・②
・・・②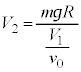 ∴
∴ 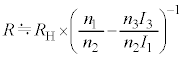 ・・・⑪
・・・⑪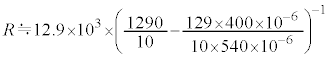
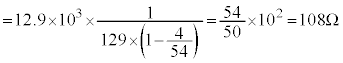 ......[答]
......[答]