������w2023�N�O�������������
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
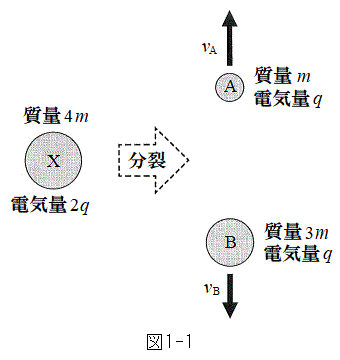 [1]�@�ȉ��̂悤�ȉ��z�I�ȕs���茴�q�jX���l����BX�̎��ʂ�
[1]�@�ȉ��̂悤�ȉ��z�I�ȕs���茴�q�jX���l����BX�̎��ʂ�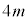 �C�d�C�ʂ͐��̒l
�C�d�C�ʂ͐��̒l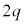 �ł���BX�̔�������T�ŁA�}1-1�Ɏ����悤�Ɏ����I�ɓ�̌��q�jA��B�ɕ���BA�̎��ʂ�m�CB�̎��ʂ�
�ł���BX�̔�������T�ŁA�}1-1�Ɏ����悤�Ɏ����I�ɓ�̌��q�jA��B�ɕ���BA�̎��ʂ�m�CB�̎��ʂ�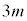 �ł���B����̍ۂ̎��ʌ�����
�ł���B����̍ۂ̎��ʌ�����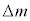 �ł��邪�A�����m�Ɣ�ׂď\���������̂ŁAX�̎��ʂ�A��B�̎��ʂ̘a�ŋߎ�����Ă���B�����̓d�C�ʂ�A��B������q�ł���B�����̌��q�j�̉^���ɂ��čl���悤�B
�ł��邪�A�����m�Ɣ�ׂď\���������̂ŁAX�̎��ʂ�A��B�̎��ʂ̘a�ŋߎ�����Ă���B�����̓d�C�ʂ�A��B������q�ł���B�����̌��q�j�̉^���ɂ��čl���悤�B
�������A���q�j�͐^���^�����Ă���A�d�͖͂����ł���B���q�j�̑����͐^�̌���c�ɔ�ׂď\���x���B���q�j�͎��_�Ƃ��Ĉ����A�ʎq�I�Ȕg�����͖����ł���B�X�̌��q�j�͈ȉ��̖�蕶�ŗ^������d��⎥��ɂ��͂������A���̌��q�j�����d���d���ɔ����͖͂����ł���B�����x�^���ɔ����d���g���˂������ł���B
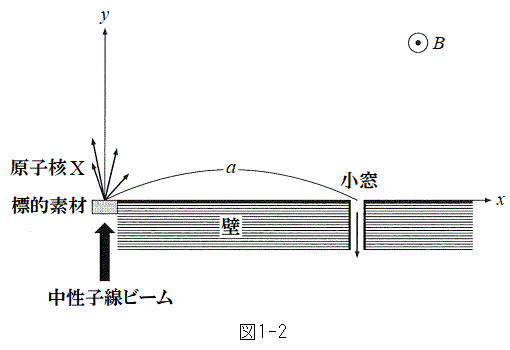 �T�@�����̌��q�jX�����A����炪����O�ɁA����̉^���G�l���M�[�������̂������W�߂邱�Ƃ��l����B�}1-2�̂悤�ɁA���W���_�ɂ���W�I�f�ނɒ����q�r�[�����Ǝ˂��A�j�������N�������ƂŁA������X�������B������X��
�T�@�����̌��q�jX�����A����炪����O�ɁA����̉^���G�l���M�[�������̂������W�߂邱�Ƃ��l����B�}1-2�̂悤�ɁA���W���_�ɂ���W�I�f�ނɒ����q�r�[�����Ǝ˂��A�j�������N�������ƂŁA������X�������B������X�� �̗̈�ɗl�X�ȑ����ŁA�l�X�ȕ����ɔ�яo���B
�̗̈�ɗl�X�ȑ����ŁA�l�X�ȕ����ɔ�яo���B �̗̈�Ɏ��ʂɐ����ɗ�����\�̌����Ɏ������xB�̈�l�Ȏ����������Bx���ɉ����Ď��ʂɐ����ȕǂ�݂��Ax����Ɍ��_���狗��a�������ꂽ�ʒu�ɏ������J����B�ǂɏՓ˂��邱�ƂȂ��A�ǖʂɐ����ɏ�����ʉ߂��錴�q�j�������W�߂�B�ȉ��̐ݖ�ɓ�����B�������A�W�I�f�ނ⏬���̑傫���͒���a�Ɣ�ׂď\���������B
�̗̈�Ɏ��ʂɐ����ɗ�����\�̌����Ɏ������xB�̈�l�Ȏ����������Bx���ɉ����Ď��ʂɐ����ȕǂ�݂��Ax����Ɍ��_���狗��a�������ꂽ�ʒu�ɏ������J����B�ǂɏՓ˂��邱�ƂȂ��A�ǖʂɐ����ɏ�����ʉ߂��錴�q�j�������W�߂�B�ȉ��̐ݖ�ɓ�����B�������A�W�I�f�ނ⏬���̑傫���͒���a�Ɣ�ׂď\���������B
(1) ��������W�߂���X��X�̉^���G�l���M�[��m�Cq�CB�Ca��p���ĕ\���B
(2) X������O�ɁA�Ȃ�ׂ������悭X���W�߂����B���_�Ő�������A������ʂ�O���ɓ�����X�̂����A�����O�ɏ�����ʉ߂��銄����f �ȏ�ɂȂ邽�߂ɕK�v�Ȏ������xB�̉����l��f�Cm�Cq�Ca�CT�̒�����K�v�Ȃ��̂�p���ĕ\���B�����Ŏ��W���ꂽX�͏\�������ŁA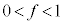 �Ƃ���B
�Ƃ���B
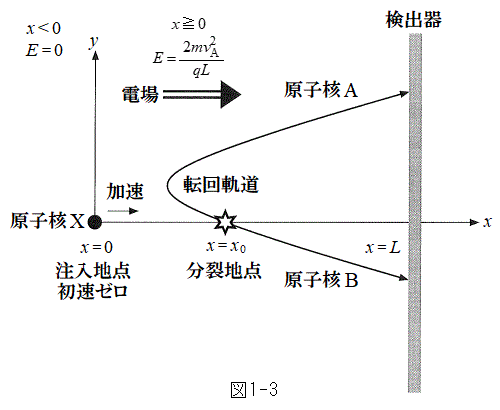 �U�@���ɁA�}1-3�Ɏ����������l����B���q�jX�����W���_�ɁA����0�Ŏ��X�ƒ�������B�����ł�
�U�@���ɁA�}1-3�Ɏ����������l����B���q�jX�����W���_�ɁA����0�Ŏ��X�ƒ�������B�����ł�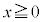 �̗̈悾���ɁAx�����̌����̈�l�ȓd��E���������Ă���AX��x���ɉ����ĉ������Ă����B
�̗̈悾���ɁAx�����̌����̈�l�ȓd��E���������Ă���AX��x���ɉ����ĉ������Ă����B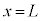 �ɂ͌��o�킪����A���q�j�̉^���G�l���M�[�Ɠd�C�ʁA���ʂ𑪂邱�Ƃ��ł���B�d��E�́A
�ɂ͌��o�킪����A���q�j�̉^���G�l���M�[�Ɠd�C�ʁA���ʂ𑪂邱�Ƃ��ł���B�d��E�́A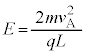 �ƂȂ�悤�ɒ�������Ă���B������
�ƂȂ�悤�ɒ�������Ă���B������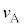 �́A�ݖ�T(3)�ɂ�����A�̑���(�}1-1�Q��)�ł���A�萔�ł���B
�́A�ݖ�T(3)�ɂ�����A�̑���(�}1-1�Q��)�ł���A�萔�ł���BX�̈ꕔ�͌��o��ɓ���O�ɗl�X�Ȓn�_�ŕ��AA��B����B���q�j�̉^������ʂ�xy���ʂɂƂ�A�ȉ��ł͎��ʐ��������̑��x��0�Ƃ���B����X�Ɠ���������x���ɉ����ĉ^������ϑ��҂̌n��X�Î~�n�ƌĂԁBX�Î~�n�ł́A���������A�͑���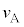 �őS�Ă̕����ɓ������m���Ŕ�яo���BX�Î~�n�ł̕��������A�̑��x�x�N�g�����Ax���ƂȂ��p�x��
�őS�Ă̕����ɓ������m���Ŕ�яo���BX�Î~�n�ł̕��������A�̑��x�x�N�g�����Ax���ƂȂ��p�x��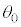 �Ƃ���B���̂Ƃ��A���������X�Î~�n�ł�A��x�����̑��x��
�Ƃ���B���̂Ƃ��A���������X�Î~�n�ł�A��x�����̑��x��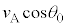 �ƕ\����B�ȉ��̐ݖ�ɓ�����B
�ƕ\����B�ȉ��̐ݖ�ɓ�����B
(1) �}1-3�ɂ���悤�ɁAX�̕���Ő�����A�̒��ɂ́A��x���o�킩�牓����������ɔ��A�]�Č��o��ɓ�����̂�����B���̂悤�ȋO����]��O���ƌĂԁBA���]��O�������ǂ�����ŁA���o��ɓ��˂�����������߂悤�B�ȉ��̕��� ����
���� �ɓ��鎮����B�ȉ��̕����Ŏw�肳�ꂽ�����ɉ����AL�C
�ɓ��鎮����B�ȉ��̕����Ŏw�肳�ꂽ�����ɉ����AL�C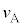 �̒�����K�v�Ȃ��̂�p����B
�̒�����K�v�Ȃ��̂�p����B ����X�̌��o��ɑ��鑬����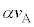 �ƕ\���ƁA�����n�_
�ƕ\���ƁA�����n�_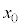 �̊��Ƃ���
�̊��Ƃ���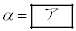 �Ə�����B�܂��A��������Ă���
�Ə�����B�܂��A��������Ă���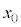 �܂ňړ����鎞�Ԃ́A
�܂ňړ����鎞�Ԃ́A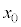 �̑����α��p���āA
�̑����α��p���āA �ƕ\����B
�ƕ\����B
�]��O���ɓ��邽�߂ɂ́AA�̏����x��x�����͕��ł���K�v������̂ŁA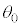 �ɑ��āAα�ŕ\��������A
�ɑ��āAα�ŕ\��������A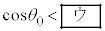 ��������B���̏�������A��������
��������B���̏�������A��������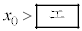 �ł͓]��O�����������Ȃ����Ƃ��킩��BA������ɔ�ꍇ�A
�ł͓]��O�����������Ȃ����Ƃ��킩��BA������ɔ�ꍇ�A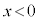 �̗̈�ɓ���ƁA���o��ɓ��B���邱�Ƃ͂Ȃ��B���������邽�߂̏����́Aα��p����
�̗̈�ɓ���ƁA���o��ɓ��B���邱�Ƃ͂Ȃ��B���������邽�߂̏����́Aα��p����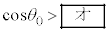 �ƕ\����B
�ƕ\����B �̂Ƃ��ɂ́AA��
�̂Ƃ��ɂ́AA��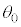 �ɂ�炸
�ɂ�炸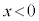 �̗̈�ɓ��邱�Ƃ͂Ȃ��B
�̗̈�ɓ��邱�Ƃ͂Ȃ��B
(2) ���o��ɓ�����A�̂����A���o���x����̓_�Ō��o���ꂽ���̂����ɒ��ڂ���B���肳���^���G�l���M�[�̎�肤��͈͂�m�C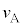 ��p���ĕ\���B
��p���ĕ\���B
(3) X�̒������J��Ԃ��A�\��������A�����o���ꂽ�B���o���ꂽA�̂����A�^���G�l���M�[��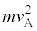 �������������q�j�̐��̊����́AX�̔�����T��
�������������q�j�̐��̊����́AX�̔�����T��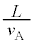 �Ɣ�ׂĂ͂邩�ɒZ���ꍇ�ƁA�t�ɂ͂邩�ɒ����ꍇ�ŁA�ǂ��炪�����Ȃ�Ɗ��҂���邩�A���R�Ƌ��ɓ�����B
�Ɣ�ׂĂ͂邩�ɒZ���ꍇ�ƁA�t�ɂ͂邩�ɒ����ꍇ�ŁA�ǂ��炪�����Ȃ�Ɗ��҂���邩�A���R�Ƌ��ɓ�����B
[��]
[2]�@���ʂ��ɑ��肷�鑕�u�ɂ��čl���悤�B
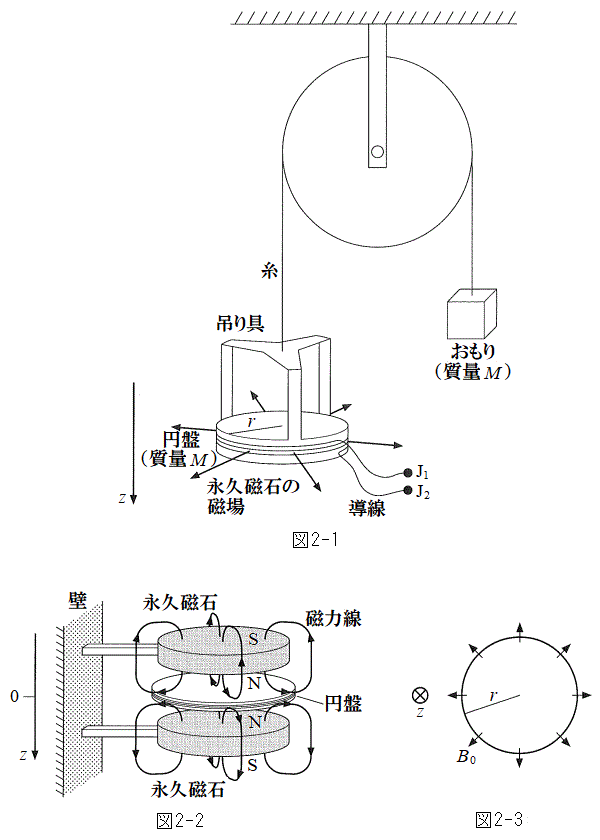 �T�@�}2-1�̂悤�ɁA���炩�ɉ�]����y�����ԂɁA���ar�C����M�̉~�Ղ��A���ʂ̖����ł��鎅�ƒ݂��Ő����ɂ艺�����Ă���B�~�Ղ̑��ʂɂ͓���������������N����Ă���B�����̊��������́A�ォ�猩���Ƃ��ɒ[�q
�T�@�}2-1�̂悤�ɁA���炩�ɉ�]����y�����ԂɁA���ar�C����M�̉~�Ղ��A���ʂ̖����ł��鎅�ƒ݂��Ő����ɂ艺�����Ă���B�~�Ղ̑��ʂɂ͓���������������N����Ă���B�����̊��������́A�ォ�猩���Ƃ��ɒ[�q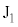 ���n�_�Ƃ��Ď��v���ł���B���Ԃ̔��Α��ɂ͎���M�̂����肪�艺�����Ă���B�~�Ղ̌����͏\���ɏ��������̂Ƃ���B
���n�_�Ƃ��Ď��v���ł���B���Ԃ̔��Α��ɂ͎���M�̂����肪�艺�����Ă���B�~�Ղ̌����͏\���ɏ��������̂Ƃ���B�~�Ղ̏㉺�ɂ͐}2-2�̂悤�ɁA��̉~�`�̉i�v����N�ɓ��m�������������悤�ɕǂɌŒ肷��B����������������z�����Ƃ�A��̎��̒��ԓ_��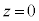 �Ƃ���B�~�Ղ́A�͂���
�Ƃ���B�~�Ղ́A�͂���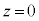 �ɔz�u����Ă���A������ۂ��Ȃ���z�����ɂ̂݉^������B�~�Ղ������͈͂ł́A�}2-3�̂悤�ɉ~�Ղ̔��a���������������ˏ�̎��ꂪ�i�v���ɂ�����A�����̈ʒu�ł̎������x�̑傫���͈��̒l
�ɔz�u����Ă���A������ۂ��Ȃ���z�����ɂ̂݉^������B�~�Ղ������͈͂ł́A�}2-3�̂悤�ɉ~�Ղ̔��a���������������ˏ�̎��ꂪ�i�v���ɂ�����A�����̈ʒu�ł̎������x�̑傫���͈��̒l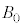 �ł���B���̎���͉~�ՂɊ����ꂽ�����݂̂ɍ�p������̂Ƃ���B
�ł���B���̎���͉~�ՂɊ����ꂽ�����݂̂ɍ�p������̂Ƃ���B
���̑��u�͐^�ɒu����Ă���B�d�͉����x��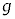 �C�^�̌�����c�Ƃ���B�~�Ղ�����������c�����\���ɏ������B���̐L�k�͂Ȃ��B�����̎��ʁA�����A��R�A���ȃC���_�N�^���X�͖�������B�܂��A�~�ՂɊ�����Ă��Ȃ������̓����́A�~�Ղ̉^���ɉe�����Ȃ��B�ȉ��̐ݖ�ɓ�����B
�C�^�̌�����c�Ƃ���B�~�Ղ�����������c�����\���ɏ������B���̐L�k�͂Ȃ��B�����̎��ʁA�����A��R�A���ȃC���_�N�^���X�͖�������B�܂��A�~�ՂɊ�����Ă��Ȃ������̓����́A�~�Ղ̉^���ɉe�����Ȃ��B�ȉ��̐ݖ�ɓ�����B
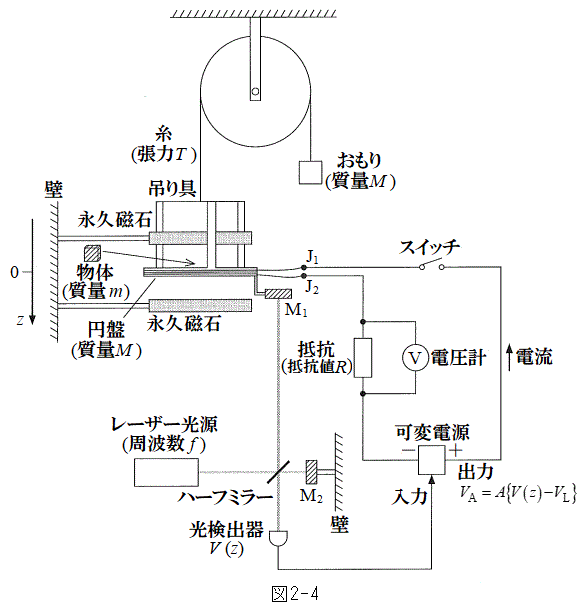 �}2-4�̂悤�ɁA�~�Ղ̈ʒu���ɑ��肵�d�C�M���ɕϊ����邽�߁A���̑��u�ɂ̓��[�U�[���v���g�ݍ��܂�Ă���B���[�U�[�������o�����g��f �̌��́A�n�[�t�~���[�ňꕔ�����˂��A�ꕔ�͓��߂���B�n�[�t�~���[�Ŕ��˂������͉~�ՂɎ��t������
�}2-4�̂悤�ɁA�~�Ղ̈ʒu���ɑ��肵�d�C�M���ɕϊ����邽�߁A���̑��u�ɂ̓��[�U�[���v���g�ݍ��܂�Ă���B���[�U�[�������o�����g��f �̌��́A�n�[�t�~���[�ňꕔ�����˂��A�ꕔ�͓��߂���B�n�[�t�~���[�Ŕ��˂������͉~�ՂɎ��t������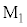 �Ŕ��˂��A�n�[�t�~���[�߂������͕ǂɌŒ肳�ꂽ��
�Ŕ��˂��A�n�[�t�~���[�߂������͕ǂɌŒ肳�ꂽ��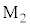 �Ŕ��˂���B
�Ŕ��˂���B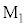 �C
�C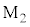 �Ŕ��˂������́A�n�[�t�~���[�ŏd�ˍ��킳������o��Ɍ������B���̌o�H�͐^�ɂ���B���̂Ƃ��A�~�Ղ̈ʒuz���ω�����ƁA���o�������̋��������ɂ��ω�����B�����o�킩��́A���o�������̋����ɔ�Ⴕ���d��
�Ŕ��˂������́A�n�[�t�~���[�ŏd�ˍ��킳������o��Ɍ������B���̌o�H�͐^�ɂ���B���̂Ƃ��A�~�Ղ̈ʒuz���ω�����ƁA���o�������̋��������ɂ��ω�����B�����o�킩��́A���o�������̋����ɔ�Ⴕ���d��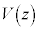 ���o�͂����B���̓d���́A
���o�͂����B���̓d���́A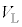 ��k�𐳂̒萔�Ƃ���
��k�𐳂̒萔�Ƃ���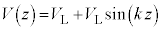 �ƕ\�����Ƃ��ł���B��
�ƕ\�����Ƃ��ł���B��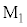 �̎��ʂ͖����ł���B
�̎��ʂ͖����ł���B
(2) f ��c��p����k��\���B
�}2-4�̉�H�Ɋ܂܂��ϓd���́A�����o��̏o�͓d������͂���ƁA���̑�������A�Ƃ���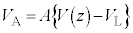 �Ȃ�d�����o�͂���B��R�lR�̒�R�ɐ�����d���~�����A������R�̏\���傫�ȓd���v�ɂ���đ��肷��B
�Ȃ�d�����o�͂���B��R�lR�̒�R�ɐ�����d���~�����A������R�̏\���傫�ȓd���v�ɂ���đ��肷��B
���܁A�~�Ղ̈ʒu��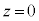 �ɖ߂��A�Î~�������B�X�C�b�`�����Ɖ~�Ղ͐Î~�𑱂����B���ɁA�~�Ղ̏�Ɏ���m�̕��̂�Â��ɒu���ƁA���̂Ɖ~�Ղ͈�̂ƂȂ��ĉ����������ɉ^�����n�߂��B
�ɖ߂��A�Î~�������B�X�C�b�`�����Ɖ~�Ղ͐Î~�𑱂����B���ɁA�~�Ղ̏�Ɏ���m�̕��̂�Â��ɒu���ƁA���̂Ɖ~�Ղ͈�̂ƂȂ��ĉ����������ɉ^�����n�߂��B
(3) �~�Ղ��艺���Ă��鎅�̒��͂�T�C���̂̑��x��v�Ƃ���B��̂ƂȂ��ĉ^�����镨�̂Ɖ~�Ղɂ͂��炭�͂̍��͂��Ak�Cm�CM�CT�CA�Cr�CN�C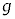 �C
�C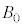 �CR�C
�CR�C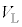 �Cv�Cz�̂����K�v�Ȃ��̂�p���ĕ\���B
�Cv�Cz�̂����K�v�Ȃ��̂�p���ĕ\���B A���\���傫���l�ł��������߁A���̂Ɖ~�Ղ͈�̂̂܂ܔ��ɏ����ȐU���ŏ㉺�ɉ^�����A���ԂƂƂ��ɂ��̐U���͌��������B���Ԃ��o�߂��ĂقڐÎ~�����ƌ��Ȃ���Ƃ��̉~�Ղ̈ʒu��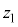 �C�d���v�̑���l�̐�Βl��
�C�d���v�̑���l�̐�Βl��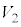 �Ƃ���B
�Ƃ���B
(4) 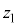 ��
��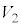 ��k�Cm�CA�Cr�CN�C
��k�Cm�CA�Cr�CN�C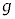 �C
�C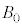 �CR�C
�CR�C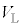 �̂����K�v�Ȃ��̂�p���ĕ\���B�������A
�̂����K�v�Ȃ��̂�p���ĕ\���B�������A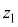 ���\���ɏ��������߁A�ߎ���
���\���ɏ��������߁A�ߎ���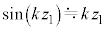 ��p���Ă��悢�B
��p���Ă��悢�B
�U�@����m�̑���ɗp������R�̒�R�lR���Ɍ��߂邱�Ƃ��l���悤�B
�����┼���̂ɓd���𗬂��A���̓d���̌����Ɛ����Ɏ����������ƁA�z�[�����ʂɂ���ēd���Ǝ���ɐ����ȕ����ɓd�ʍ���������B���̂悤�ȓd�q���i���z�[���f�q�ƌĂԁB�z�[�����ʂ̂����A�ʎq�z�[�����ʂƂ�������ȏꍇ�ɂ́A�������d�ʍ��Ɠd���̔�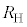 �̒l�͌����Ɍ��܂��Ă���A��R�l�̊�ƂȂ�B
�̒l�͌����Ɍ��܂��Ă���A��R�l�̊�ƂȂ�B
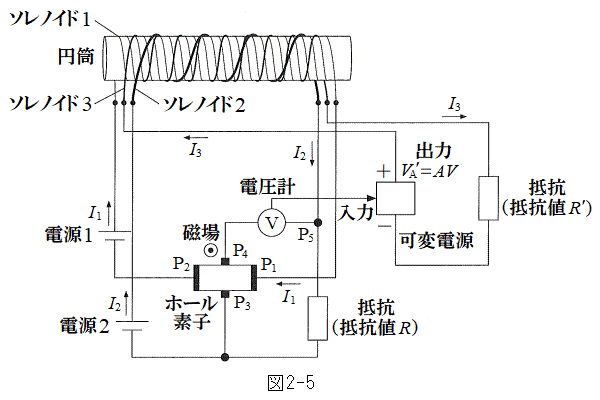
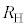 ����Ƃ��Ė��m�̒�R�lR�𑪒肷�邽�߁A�}2-5�Ɏ�����H��p����B�z�[���f�q�ɂ́A���ʂɐ����ŗ�����\�Ɍ��������ꂪ�������Ă���A
����Ƃ��Ė��m�̒�R�lR�𑪒肷�邽�߁A�}2-5�Ɏ�����H��p����B�z�[���f�q�ɂ́A���ʂɐ����ŗ�����\�Ɍ��������ꂪ�������Ă���A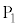 ����
����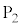 �̌����ɓd��
�̌����ɓd��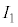 �𗬂��ƁA
�𗬂��ƁA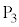 ����Ƃ���
����Ƃ���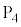 �̓d�ʂ�
�̓d�ʂ�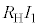 �ƂȂ�B
�ƂȂ�B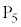 ����Ƃ���
����Ƃ���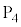 �̓d��V�������R�̏\���傫�ȓd���v�ő��肵�A���̑傫�ȑ�����A�����ϓd���ɓ��͂���B�ϓd���͓d��
�̓d��V�������R�̏\���傫�ȓd���v�ő��肵�A���̑傫�ȑ�����A�����ϓd���ɓ��͂���B�ϓd���͓d��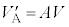 ���o�͂��A��R�l
���o�͂��A��R�l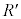 �̒�R�ɐڑ�����Ă���B�z�[���f�q�́A
�̒�R�ɐڑ�����Ă���B�z�[���f�q�́A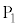 ��
��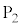 �̊ԂɗL���̒�R�l�����B
�̊ԂɗL���̒�R�l�����B
�\���m�C�h1�C2�C3�͔䓧����1�̈�̉~���Ɋ�����Ă���A�P�ʒ���������̊����͂��ꂼ��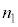 �C
�C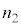 �C
�C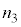 �ł���B�\���m�C�h2��3�͓��������ɁA�\���m�C�h1�͂����Ƃ͋t�����Ɋ�����Ă���B�d��1�C�d��2�C�ϓd�����痬���d�������ꂼ��
�ł���B�\���m�C�h2��3�͓��������ɁA�\���m�C�h1�͂����Ƃ͋t�����Ɋ�����Ă���B�d��1�C�d��2�C�ϓd�����痬���d�������ꂼ��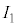 �C
�C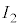 �C
�C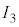 �Ƃ��A���ꂼ�ꂪ�\���m�C�h1�C2�C3�ɗ���Ă���B
�Ƃ��A���ꂼ�ꂪ�\���m�C�h1�C2�C3�ɗ���Ă���B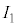 ��
��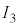 �͓d���ɓ������ꂽ�d���v�ő��肵�Ă���B�\���m�C�h�̓����̒�R�͖����ł���B�ȉ��̐ݖ�ɓ�����B
�͓d���ɓ������ꂽ�d���v�ő��肵�Ă���B�\���m�C�h�̓����̒�R�͖����ł���B�ȉ��̐ݖ�ɓ�����B
(1) 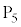 ����Ƃ���
����Ƃ���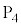 �̓d��V�ƃ\���m�C�h�����̎���H�̑傫�����A
�̓d��V�ƃ\���m�C�h�����̎���H�̑傫�����A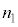 �C
�C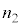 �C
�C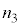 �C
�C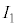 �C
�C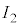 �C
�C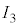 �CR�C
�CR�C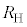 �̂����K�v�Ȃ��̂�p���Ă��ꂼ��\���B
�̂����K�v�Ȃ��̂�p���Ă��ꂼ��\���B
(2) �ȉ��̋L�q�ɂ��āA ��
�� �ɂ��Ă͂܂鎮���A
�ɂ��Ă͂܂鎮���A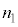 �C
�C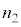 �C
�C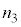 �C
�C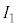 �C
�C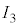 �CR�C
�CR�C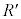 �̂����K�v�Ȃ��̂�p���ĕ\���B
�̂����K�v�Ȃ��̂�p���ĕ\���B ���C�Z���T�[�Ń\���m�C�h�����̎���H�𑪒肵�A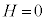 �ƂȂ�悤�ɓd��1�̓d���ɂ��
�ƂȂ�悤�ɓd��1�̓d���ɂ��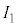 �������B���̂Ƃ��A
�������B���̂Ƃ��A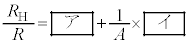 �ƕ\�����Ƃ��ł���B������A���傫���̂ŁA�ߎ���
�ƕ\�����Ƃ��ł���B������A���傫���̂ŁA�ߎ���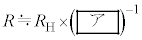 ��������B
��������B �\���m�C�h�̊��������܂��I�Ԃ��ƂŁA�d���̑���덷�ɔ�ׂĒ�R�lR�̑���덷�𑊑ΓI�ɏ��������邱�Ƃ��ł���B�ʎq�z�[�����ʂł�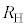 �́A�����萔�ł���v�����N�萔h�C�d�C�f��e�Ǝ��R��p��p����
�́A�����萔�ł���v�����N�萔h�C�d�C�f��e�Ǝ��R��p��p����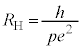 �ƕ\����B�����ł́A
�ƕ\����B�����ł́A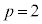 �C
�C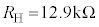 �̑f�q��p����B���܁A���肵������R�lR��
�̑f�q��p����B���܁A���肵������R�lR��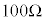 ���x�ł��邱�Ƃ�����O�ɂ킩���Ă���B����덷�����������邽�߂ɁA
���x�ł��邱�Ƃ�����O�ɂ킩���Ă���B����덷�����������邽�߂ɁA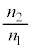 ��
��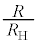 �Ƌ߂��l�ƂȂ�A
�Ƌ߂��l�ƂȂ�A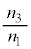 ���������Ȃ�悤�Ɋ����̔��I�сA
���������Ȃ�悤�Ɋ����̔��I�сA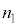 �F
�F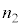 �F
�F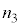 = 1290�F10�F129�Ƃ����B
= 1290�F10�F129�Ƃ����B
(3) �d��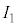 ��
��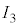 �̑���l�Ɛ^�̒l�A����ђ�R�lR�̐^�̒l��\2-1�Ɏ����B�d���̑��Ό덷��10�����x�ł���B
�̑���l�Ɛ^�̒l�A����ђ�R�lR�̐^�̒l��\2-1�Ɏ����B�d���̑��Ό덷��10�����x�ł���B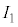 �C
�C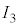 �̑���l�Ɛݖ�U(2)�œ����ߎ�������A��R�lR�̑���l��L������3���ŋ��߂�B�܂��A���̒�R����̑��Ό덷�͉������A�L������1���œ�����B
�̑���l�Ɛݖ�U(2)�œ����ߎ�������A��R�lR�̑���l��L������3���ŋ��߂�B�܂��A���̒�R����̑��Ό덷�͉������A�L������1���œ�����B
[��]
[3]�@�S���Ђ���L���ƁA���̒����ɖ߂낤�Ƃ��镜���͂��͂��炭�B����ŃS������L���čL����ƁA���̖ʐς����������悤�Ƃ���͂��͂��炭�B���̗͂��͂ƌĂԁB�\���ɏ������ʐ�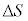 �����S�������L����̂ɕK�v�Ȏd��
�����S�������L����̂ɕK�v�Ȏd�� ��
��
�ŗ^������B������σ��[��/����]�̎����������A�����͂̑傫��������Â��鐳�̌W���ł���B�S�����łł������D��c��܂���ƁA�����͂ɂ�蕗�D�̓����͊O�C�����������Ȃ�B�O�C���� �ŏ�Ɉ��Ƃ���B�d�͂����A���D�͏�ɋ��`��ۂ��j�Ȃ����̂Ƃ��āA�ȉ��̐ݖ�ɓ�����B
�ŏ�Ɉ��Ƃ���B�d�͂����A���D�͏�ɋ��`��ۂ��j�Ȃ����̂Ƃ��āA�ȉ��̐ݖ�ɓ�����B
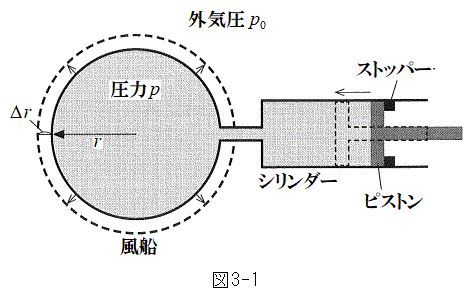 �T�@�}3-1�̂悤�ɔ��ar�̕��D�ƃV�����_�[���ڑ�����Ă���B�V�����_�[�ɂ͊��炩�ɓ����s�X�g�������Ă���A�͂��߃s�X�g���̓X�g�b�p�[�̈ʒu�ŐÎ~���Ă���B���D�ƃV�����_�[���͉t�̂Ŗ�������Ă���A�t�̂̈���p�͈�l�ŁA�t�̂̑̐ς͈��Ƃ���B�S�����̌��݂����A�W��σ�͈��Ƃ���B
�T�@�}3-1�̂悤�ɔ��ar�̕��D�ƃV�����_�[���ڑ�����Ă���B�V�����_�[�ɂ͊��炩�ɓ����s�X�g�������Ă���A�͂��߃s�X�g���̓X�g�b�p�[�̈ʒu�ŐÎ~���Ă���B���D�ƃV�����_�[���͉t�̂Ŗ�������Ă���A�t�̂̈���p�͈�l�ŁA�t�̂̑̐ς͈��Ƃ���B�S�����̌��݂����A�W��σ�͈��Ƃ���B
(1) �s�X�g����������蓮�������D��c��܂����Ƃ���A�}3-1�̂悤�ɔ��a������ �����傫���Ȃ����B�s�X�g�������̂ɗv�����d����
�����傫���Ȃ����B�s�X�g�������̂ɗv�����d����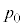 �Cp�Cr�C
�Cp�Cr�C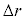 ��p���ĕ\���B�������A
��p���ĕ\���B�������A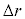 �͏\���������A
�͏\���������A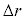 �̓ȏ�̍��͖������Ă悢�B
�̓ȏ�̍��͖������Ă悢�B
(2) �ݖ�T(1)�ŕ��D��c��܂����Ƃ��ɁA���D�̕\�ʐς�傫������̂ɗv�����d����r�C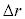 �Cσ��p���ĕ\���B�������A
�Cσ��p���ĕ\���B�������A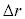 �͏\���������A
�͏\���������A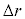 �̓ȏ�̍��͖������Ă悢�B
�̓ȏ�̍��͖������Ă悢�B
(3) p��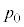 �Cr�Cσ��p���ĕ\���B�������A�s�X�g������ĂȂ����d���́A�S�Ă̕��D�̕\�ʐς�傫������̂ɗv����d���ɕϊ��������̂Ƃ���B
�Cr�Cσ��p���ĕ\���B�������A�s�X�g������ĂȂ����d���́A�S�Ă̕��D�̕\�ʐς�傫������̂ɗv����d���ɕϊ��������̂Ƃ���B
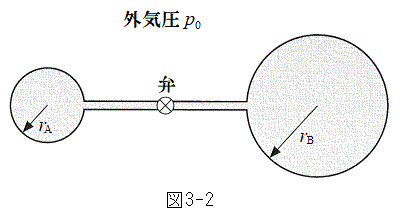 �U�@�}3-2�̂悤�ɁA�����ȕق������ׂ��ǂ̗��[�ɌW��σ�̕��D�����Ă���A���ɂ͓������x�̗��z�C�̂�����������A�C�̂̉��x�͏�Ɉ��ɕۂ���Ă���B�ŏ��A�ق͕��Ă���A���D�̔��a�͂��ꂼ��
�U�@�}3-2�̂悤�ɁA�����ȕق������ׂ��ǂ̗��[�ɌW��σ�̕��D�����Ă���A���ɂ͓������x�̗��z�C�̂�����������A�C�̂̉��x�͏�Ɉ��ɕۂ���Ă���B�ŏ��A�ق͕��Ă���A���D�̔��a�͂��ꂼ��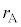 �C
�C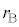 �ł���B�Ǔ��ƕق̑̐ρA�S�����̌��݂����A�W��σ�͈��Ƃ���B�܂��A���D�����ڂ݂������ꍇ�A���D�̔��a�͖����ł���قǏ������Ȃ���̂Ƃ���B
�ł���B�Ǔ��ƕق̑̐ρA�S�����̌��݂����A�W��σ�͈��Ƃ���B�܂��A���D�����ڂ݂������ꍇ�A���D�̔��a�͖����ł���قǏ������Ȃ���̂Ƃ���B
(1) 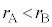 �̏ꍇ�ɕق��J���ċN����ω��ɂ��āA��
�̏ꍇ�ɕق��J���ċN����ω��ɂ��āA�� ��
�� �ɓ���ł��K�Ȍ���I�����@�`�C����I�ׁB�܂��A�������ɂ��Ă̗��R���Ȍ��ɓ�����B
�ɓ���ł��K�Ȍ���I�����@�`�C����I�ׁB�܂��A�������ɂ��Ă̗��R���Ȍ��ɓ�����B �ق��J���ƋC�̂͊ǂ�ʂ�A���a�� ���D�����������̕��D�Ɉڂ��B�\�����Ԃ��o������̕��D�́A�Е������a
���D�����������̕��D�Ɉڂ��B�\�����Ԃ��o������̕��D�́A�Е������a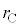 �ŁA
�ŁA �B
�B
�@�@�傫���@�@�A�@������
�B�@���������a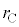 �ɂȂ�@�@�C�@�����͂��ڂ݂����Ă���
�ɂȂ�@�@�C�@�����͂��ڂ݂����Ă���
�V�@���ۂ̕��D�ł́A�����͂̑傫��������Â���W��σ�͈��ł͂Ȃ��A���ar�̊��Ƃ��ĕω�����B�ȉ��̐ݖ�ł́A���D�̌W��σ�͊W��
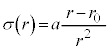 �@(
�@(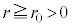 )
)�ɏ]���Ɖ��肷��B������a�� �͐��̒萔�ł���A���x�ɂ���ĕω����Ȃ����̂Ƃ���B���D�̔��a�͏��
�͐��̒萔�ł���A���x�ɂ���ĕω����Ȃ����̂Ƃ���B���D�̔��a�͏�� ���傫�����̂Ƃ���B
���傫�����̂Ƃ���B
 (1) �}3-3�̂悤�ɁA���z�C�̂���������A���D�̔��a���ǂ����
(1) �}3-3�̂悤�ɁA���z�C�̂���������A���D�̔��a���ǂ����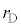 �̏ꍇ���l����B�ق��J���ĕЕ��̕��D����ł킸���ɂ��ڂ܂�����A���������Ƃ���A���D�̑傫���͕ω����A���a���قȂ��̕��D�ƂȂ����B
�̏ꍇ���l����B�ق��J���ĕЕ��̕��D����ł킸���ɂ��ڂ܂�����A���������Ƃ���A���D�̑傫���͕ω����A���a���قȂ��̕��D�ƂȂ����B ���������ׂ����������߂�B�������A�C�̂̉��x�͈��ɕۂ���Ă���Ƃ���B
���������ׂ����������߂�B�������A�C�̂̉��x�͈��ɕۂ���Ă���Ƃ���B
(2) �ݖ�V(1)�ŏ\�����Ԃ��o������A�ق��J�����܂܁A��̕��D���̋C�̂̉��x���������킸���ɏグ���B���D�̓����͍����Ȃ������A�Ⴍ�Ȃ������A���R�Ƌ��ɓ�����B�K�v�Ȃ�A�}��p���Ă悢�B
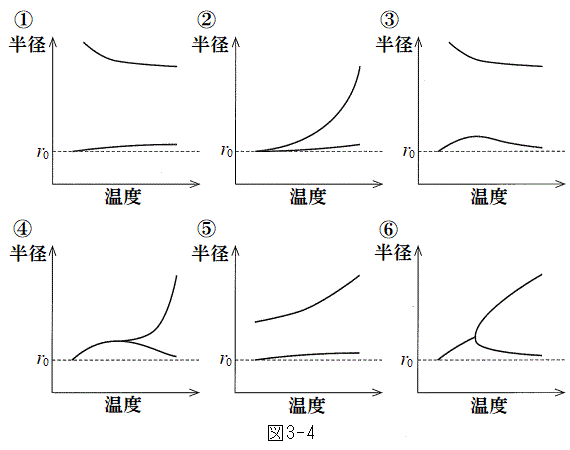 (3) �ݖ�V(2)�ŏ\�����Ԃ��o������A���x�͕��D���̋C�̂̉��x���������Ɖ������B��̕��D�̔��a�����x�̊��Ƃ��Đ}������Ƃ��A�ł��K�Ȃ��̂�}3-4�̇@�`�E�����I�ׁB
(3) �ݖ�V(2)�ŏ\�����Ԃ��o������A���x�͕��D���̋C�̂̉��x���������Ɖ������B��̕��D�̔��a�����x�̊��Ƃ��Đ}������Ƃ��A�ł��K�Ȃ��̂�}3-4�̇@�`�E�����I�ׁB
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 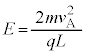 �ƂȂ�悤�ɒ�������Ă���B������
�ƂȂ�悤�ɒ�������Ă���B������