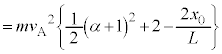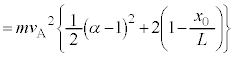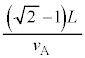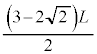���啨�� '23 �N�O�� [1] �ȉ��̂悤�ȉ��z�I�ȕs���茴�q�j X ���l����B X �̎��ʂ� X �̔������� T �ŁA�} 1-1 �Ɏ����悤�Ɏ����I�ɓ�̌��q�j A �� B �ɕ���B A �̎��ʂ� m �C B �̎��ʂ� m �Ɣ�ׂď\���������̂ŁA X �̎��ʂ� A �� B �̎��ʂ̘a�ŋߎ�����Ă���B�����̓d�C�ʂ� A �� B ������ q �ł���B�����̌��q�j�̉^���ɂ��čl���悤�B c �ɔ�ׂď\���x���B���q�j�͎��_�Ƃ��Ĉ����A�ʎq�I�Ȕg�����͖����ł���B�X�̌��q�j�͈ȉ��̖�蕶�ŗ^������d��⎥��ɂ��͂������A���̌��q�j�����d���d���ɔ����͖͂����ł���B�����x�^���ɔ����d���g���˂������ł���B �T�@�����̌��q�j X �����A����炪����O�ɁA����̉^���G�l���M�[�������̂������W�߂邱�Ƃ��l����B�} 1-2 �̂悤�ɁA���W���_�ɂ���W�I�f�ނɒ����q�r�[�����Ǝ˂��A�j�������N�������ƂŁA������ X �������B������ X �� B �̈�l�Ȏ����������B x ���ɉ����Ď��ʂɐ����ȕǂ�݂��A x ����Ɍ��_���狗�� a �������ꂽ�ʒu�ɏ������J����B�ǂɏՓ˂��邱�ƂȂ��A�ǖʂɐ����ɏ�����ʉ߂��錴�q�j�������W�߂�B�ȉ��̐ݖ�ɓ�����B�������A�W�I�f�ނ⏬���̑傫���͒��� a �Ɣ�ׂď\���������B
(1) ��������W�߂���X�� X �̉^���G�l���M�[�� m �C q �C B �C a ��p���ĕ\���B
(2) X ������O�ɁA�Ȃ�ׂ������悭 X ���W�߂����B���_�Ő�������A������ʂ�O���ɓ����� X �̂����A�����O�ɏ�����ʉ߂��銄���� f �ȏ�ɂȂ邽�߂ɕK�v�Ȏ������x B �̉����l�� f �C m �C q �C a �C T �̒�����K�v�Ȃ��̂�p���ĕ\���B�����Ŏ��W���ꂽ X �͏\�������ŁA
�U�@���ɁA�} 1-3 �Ɏ����������l����B���q�j X �����W���_�ɁA���� 0 �Ŏ��X�ƒ�������B�����ł� x �����̌����̈�l�ȓd�� E ���������Ă���A X �� x ���ɉ����ĉ������Ă����B E �́A (3) �ɂ����� A �̑��� ( �} 1-1 �Q�� ) �ł���A�萔�ł���B X �̈ꕔ�͌��o��ɓ���O�ɗl�X�Ȓn�_�ŕ��A A �� B ����B���q�j�̉^������ʂ� xy ���ʂɂƂ�A�ȉ��ł͎��ʐ��������̑��x�� 0 �Ƃ���B���� X �Ɠ��������� x ���ɉ����ĉ^������ϑ��҂̌n�� X �Î~�n�ƌĂԁB X �Î~�n�ł́A��������� A �͑��� X �Î~�n�ł̕�������� A �̑��x�x�N�g�����A x ���ƂȂ��p�x�� X �Î~�n�ł� A �� x �����̑��x�� (1) �} 1-3 �ɂ���悤�ɁA X �̕���Ő����� A �̒��ɂ́A��x���o�킩�牓����������ɔ��A�]�Č��o��ɓ�����̂�����B���̂悤�ȋO����]��O���ƌĂԁB A ���]��O�������ǂ�����ŁA���o��ɓ��˂�����������߂悤�B�ȉ��̕��� L �C ���� X �̌��o��ɑ��鑬���� α ��p���āA A �̏����x�� x �����͕��ł���K�v������̂ŁA α �ŕ\��������A A ������ɔ�ꍇ�A α ��p���� A ��
(2) ���o��ɓ����� A �̂����A���o��� x ����̓_�Ō��o���ꂽ���̂����ɒ��ڂ���B���肳���^���G�l���M�[�̎�肤��͈͂� m �C
(3) X �̒������J��Ԃ��A�\�������� A �����o���ꂽ�B���o���ꂽ A �̂����A�^���G�l���M�[�� X �̔����� T ��
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�� �@���Z�����͈̔͑S�ʂɓn�鑍�����ł��B α �� 2 ����A�ǂ�����ɗv�������̂ŁA�������₷�����ł��B �T�@���W���_�����яo���� X �������ɂ��傤�Ǔ��邽�߂ɂ́A X ������ɂ��͂��āA�A���a X �̑����� v �Ƃ���ƁA���ꂪ X �ɋy�ڂ��͂́A�傫�� �t���~���O����̖@�� ���A�����͉~�̒��S�Ɍ����������ł��B
......[ �� ]
(2) X �����a t �́A�����̋����𑬂��Ŋ����āA�@���A �@����A �������� T �Ȃ̂ŁA�����O�ɏ�����ʉ߂��銄���������l f �ɂȂ�Ƃ��A�܂�A�������x B �������l�ɂȂ�Ƃ��A
���D X �̊����� X �̊����� ���ӂ� 2 ���Ƃ��� �ΐ� ���Ƃ�ƁA�A���A
(3) �����O�� X �̉^���ʂ� y ������ 0 �C�����̉^���ʂ� y �����́A A �� B �� �^���ʕۑ� ���A �@�� �@����B ���ʌ����ɑΉ�����G�l���M�[ A �C B �̉^���G�l���M�[ �G�l���M�[�ۑ� ���A 2 �{���ćB��p����ƁA
�U (1) xy ���W�n���猩�āA��������� A �̌��o��ɑ��鏉���x�� x ������ X �̑��x�� x ������ X �Î~�n���猩�� A �� ���Α��x �� x ������ �@�� �@����C ���D��蕶�ɁA���ׂĂ̕����ɓ��m���Ŕ�яo���A�Ə�����Ă���̂ŁA xy ���W�n���猩����������� A �̑��x�́A ���萔�Ȃ̂ŁA X �� x �����̌����Ɉ��� �d�C�� ���� x ������ �������x�^�� �����܂��B X �� x �����̉^���������́A�����x�� �@�� �@����D X �͏��� 0 �ō��W���_���яo���̂ŁA�������x�^���̌������A
�@�� �@����E ���� X �� x ���������Ɉړ����Ă����̂ŁA ......[ �A ] ��������Ă��� �C �E��� �@�� �C ] A �̏����x�� x ������ �@�� �E ] ���D xy ���W�n�Ō��āA [ �E ] �̏����́A�]��O���ɓ��邽�߂̏����ł����āA [ �E ] �����Ȃ� A �́A����� x ���������ɓ����n�ߓ]�邱�ƂȂ����ڌ��o��Ɍ��������Ƃɒ��ӂ��Ă��������B
�Ȃ̂ŁA [ �E ] ���� (X �Î~�n�Ō��� x ���������ɔ�яo�����̂��܂߂āA xy ���W�n�ł͑S���� x ���������ɔ�яo�� ) �B�E���A �@�� �G ] [ �E ] �̏�������������ĕ�������ɔ�ꍇ�A A �́A���̓d�C�� x ���������ɓ������x�^�������܂��B���̉����x�� A �� x �������̉^���������́A �C �]��ʒu�� A �̑����� 0 �ɂȂ�̂ŁA�������x�^���̌������A A �� α ��p���ē�����̂ŇE��p���āA �����A����ɔ�ꍇ���l����̂ŁA �� �I ] �@����G ���D��蕶�ł� [ �I ] �̌��ʂŁA [ �I ] �̏����� �@�� �E���A ......[ �J ]
(2) ���o��� x ����̓_�ɓ��B����A�Ƃ������Ƃ́A��������� A �̑��x�� y ���������� 0 �̂��́A�܂�A A �̉^���G�l���M�[�́A�C�� ( �Ƃ��āA (i) �C����� A �̉^���G�l���M�[ K �́A �E�ɂ��A α ��p���ĕ\���ƁA
��� ( �� �E ) �C����āA K �� ( 2 �����̍ő�ŏ� ���Q�� ) �B����āA �@����H (ii) �C����� xy ���W�n�Ō��āA�]�Ă��猟�o��Ɍ��������̂ƁA���ڌ��o��Ɍ��������̂����݂��܂��B���̏ꍇ�A�]����̂��A�]��㕪���n�_ A �͈��̓d�C�͂��ē������x�^�� ( ����������˂ŁA�����x u �œ����グ�āA�����グ���ʒu�ɖ߂��Ă����Ƃ��̑��x�� ) ����̂ŁA��������̉^���G�l���M�[�Ɠ������Ȃ�܂��B����āA�]����̂��]�Ȃ����̂��A (i) �Ɠ��l�ɁA���o�퓞�B���_�ł� A �̉^���G�l���M�[ K �́A �G�� [ �I ] �̒��D���A K �� α �̒P���������ŁA �@����I �H�C�I���A���o�����^���G�l���M�[ K �͈̔͂́A
�C ......[ �� ]
(3) X �̔����� T �� ( �� �E ) �� L �ɔ�ׂĂ͂邩�ɏ������Ȃ�A����� A �̊������傫���Ȃ�܂��B T �� A �̊������������A�I�ʼn^���G�l���M�[�� A �̊������������܂��B�^���G�l���M�[�� X �̔����� T �� ......[ �� ] ���D�킩��ɂ����̂ŁA (2)[ �C ] �� ( ����܂ł̎��� ) �ɂ��āA�\�ɂ܂Ƃ߂Đ������Ă����܂��B (2)(i) �� (ii) �� ( ���Ȃ���� A �͌��o����܂��� ) �B�\���́u A �̓����v�́A X �Î~�n�Ō��� x ���������ɔ�яo���� A �́A xy ���W�n�ł̓����ł��B 0 ��� ��� ��� α 0 ��� ��� 1 ��� 0 ��� ��� ��� L �@ K �@ �@ ��� ��� A �̓��� �@ �ɓ��� �@ �]��㌟�o��ɓ��B �@ �]��Ȃ�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@ ���啨�� TOP �@�@ ���� TOP �@�@ TOP �y�[�W�ɖ߂� �y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B �e���̒��쌠�� © 2005-2024 (�L)����� ��w�y�w�m ���������t���I ���n��w�l�b�g�m ��w�y�w�m (���ē��������� )������́A������܂Ń��[�� �� 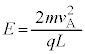 �ƂȂ�悤�ɒ�������Ă���B������
�ƂȂ�悤�ɒ�������Ă���B������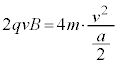
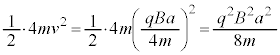 ......[��]
......[��]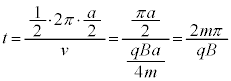 �@����A
�@����A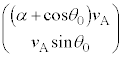 �ł��B
�ł��B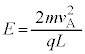 �����ŁA
�����ŁA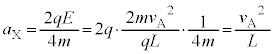 �@����D
�@����D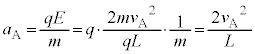
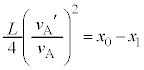
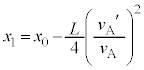 �@����F
�@����F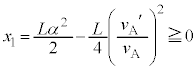
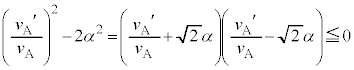
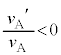 �ł��B�܂��A
�ł��B�܂��A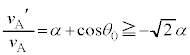
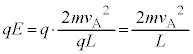 ����̂ŁA���o�퓞�B���_�ł�A�̉^���G�l���M�[K�́A
����̂ŁA���o�퓞�B���_�ł�A�̉^���G�l���M�[K�́A