���啨��'23�N�O��[3]
�S���Ђ���L���ƁA���̒����ɖ߂낤�Ƃ��镜���͂��͂��炭�B����ŃS������L���čL����ƁA���̖ʐς����������悤�Ƃ���͂��͂��炭�B���̗͂��͂ƌĂԁB�\���ɏ������ʐ�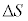 �����S�������L����̂ɕK�v�Ȏd��
�����S�������L����̂ɕK�v�Ȏd��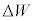 ��
��
�ŗ^������B������σ��[��/����]�̎����������A�����͂̑傫��������Â��鐳�̌W���ł���B�S�����łł������D��c��܂���ƁA�����͂ɂ�蕗�D�̓����͊O�C�����������Ȃ�B�O�C����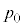 �ŏ�Ɉ��Ƃ���B�d�͂����A���D�͏�ɋ��`��ۂ��j�Ȃ����̂Ƃ��āA�ȉ��̐ݖ�ɓ�����B
�ŏ�Ɉ��Ƃ���B�d�͂����A���D�͏�ɋ��`��ۂ��j�Ȃ����̂Ƃ��āA�ȉ��̐ݖ�ɓ�����B
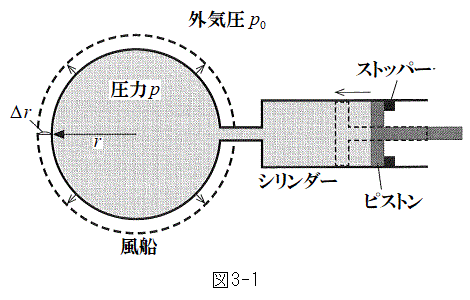 �T�@�}3-1�̂悤�ɔ��ar�̕��D�ƃV�����_�[���ڑ�����Ă���B�V�����_�[�ɂ͊��炩�ɓ����s�X�g�������Ă���A�͂��߃s�X�g���̓X�g�b�p�[�̈ʒu�ŐÎ~���Ă���B���D�ƃV�����_�[���͉t�̂Ŗ�������Ă���A�t�̂̈���p�͈�l�ŁA�t�̂̑̐ς͈��Ƃ���B�S�����̌��݂����A�W��σ�͈��Ƃ���B
�T�@�}3-1�̂悤�ɔ��ar�̕��D�ƃV�����_�[���ڑ�����Ă���B�V�����_�[�ɂ͊��炩�ɓ����s�X�g�������Ă���A�͂��߃s�X�g���̓X�g�b�p�[�̈ʒu�ŐÎ~���Ă���B���D�ƃV�����_�[���͉t�̂Ŗ�������Ă���A�t�̂̈���p�͈�l�ŁA�t�̂̑̐ς͈��Ƃ���B�S�����̌��݂����A�W��σ�͈��Ƃ���B
(1) �s�X�g����������蓮�������D��c��܂����Ƃ���A�}3-1�̂悤�ɔ��a������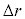 �����傫���Ȃ����B�s�X�g�������̂ɗv�����d����
�����傫���Ȃ����B�s�X�g�������̂ɗv�����d����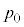 �Cp�Cr�C
�Cp�Cr�C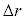 ��p���ĕ\���B�������A
��p���ĕ\���B�������A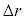 �͏\���������A
�͏\���������A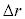 �̓ȏ�̍��͖������Ă悢�B
�̓ȏ�̍��͖������Ă悢�B
(2) �ݖ�T(1)�ŕ��D��c��܂����Ƃ��ɁA���D�̕\�ʐς�傫������̂ɗv�����d����r�C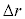 �Cσ��p���ĕ\���B�������A
�Cσ��p���ĕ\���B�������A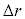 �͏\���������A
�͏\���������A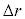 �̓ȏ�̍��͖������Ă悢�B
�̓ȏ�̍��͖������Ă悢�B
(3) p��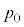 �Cr�Cσ��p���ĕ\���B�������A�s�X�g������ĂȂ����d���́A�S�Ă̕��D�̕\�ʐς�傫������̂ɗv����d���ɕϊ��������̂Ƃ���B
�Cr�Cσ��p���ĕ\���B�������A�s�X�g������ĂȂ����d���́A�S�Ă̕��D�̕\�ʐς�傫������̂ɗv����d���ɕϊ��������̂Ƃ���B
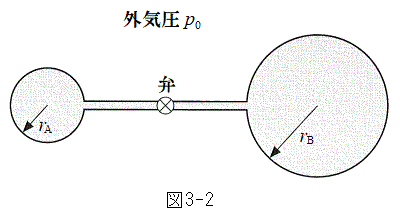 �U�@�}3-2�̂悤�ɁA�����ȕق������ׂ��ǂ̗��[�ɌW��σ�̕��D�����Ă���A���ɂ͓������x�̗��z�C�̂�����������A�C�̂̉��x�͏�Ɉ��ɕۂ���Ă���B�ŏ��A�ق͕��Ă���A���D�̔��a�͂��ꂼ��
�U�@�}3-2�̂悤�ɁA�����ȕق������ׂ��ǂ̗��[�ɌW��σ�̕��D�����Ă���A���ɂ͓������x�̗��z�C�̂�����������A�C�̂̉��x�͏�Ɉ��ɕۂ���Ă���B�ŏ��A�ق͕��Ă���A���D�̔��a�͂��ꂼ��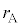 �C
�C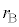 �ł���B�Ǔ��ƕق̑̐ρA�S�����̌��݂����A�W��σ�͈��Ƃ���B�܂��A���D�����ڂ݂������ꍇ�A���D�̔��a�͖����ł���قǏ������Ȃ���̂Ƃ���B
�ł���B�Ǔ��ƕق̑̐ρA�S�����̌��݂����A�W��σ�͈��Ƃ���B�܂��A���D�����ڂ݂������ꍇ�A���D�̔��a�͖����ł���قǏ������Ȃ���̂Ƃ���B
(1) 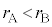 �̏ꍇ�ɕق��J���ċN����ω��ɂ��āA��
�̏ꍇ�ɕق��J���ċN����ω��ɂ��āA�� ��
�� �ɓ���ł��K�Ȍ���I�����@�`�C����I�ׁB�܂��A�������ɂ��Ă̗��R���Ȍ��ɓ�����B
�ɓ���ł��K�Ȍ���I�����@�`�C����I�ׁB�܂��A�������ɂ��Ă̗��R���Ȍ��ɓ�����B �ق��J���ƋC�̂͊ǂ�ʂ�A���a�� ���D�����������̕��D�Ɉڂ��B�\�����Ԃ��o������̕��D�́A�Е������a
���D�����������̕��D�Ɉڂ��B�\�����Ԃ��o������̕��D�́A�Е������a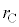 �ŁA
�ŁA �B
�B
�@�@�傫���@�@�A�@������
�B�@���������a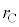 �ɂȂ�@�@�C�@�����͂��ڂ݂����Ă���
�ɂȂ�@�@�C�@�����͂��ڂ݂����Ă���
�V�@���ۂ̕��D�ł́A�����͂̑傫��������Â���W��σ�͈��ł͂Ȃ��A���ar�̊��Ƃ��ĕω�����B�ȉ��̐ݖ�ł́A���D�̌W��σ�͊W��
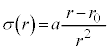 �@(
�@(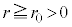 )
)�ɏ]���Ɖ��肷��B������a��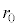 �͐��̒萔�ł���A���x�ɂ���ĕω����Ȃ����̂Ƃ���B���D�̔��a�͏��
�͐��̒萔�ł���A���x�ɂ���ĕω����Ȃ����̂Ƃ���B���D�̔��a�͏��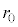 ���傫�����̂Ƃ���B
���傫�����̂Ƃ���B
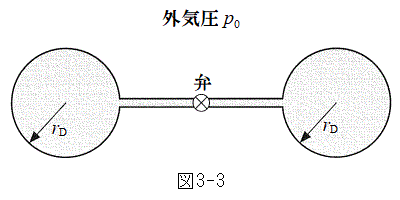 (1) �}3-3�̂悤�ɁA���z�C�̂���������A���D�̔��a���ǂ����
(1) �}3-3�̂悤�ɁA���z�C�̂���������A���D�̔��a���ǂ����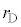 �̏ꍇ���l����B�ق��J���ĕЕ��̕��D����ł킸���ɂ��ڂ܂�����A���������Ƃ���A���D�̑傫���͕ω����A���a���قȂ��̕��D�ƂȂ����B
�̏ꍇ���l����B�ق��J���ĕЕ��̕��D����ł킸���ɂ��ڂ܂�����A���������Ƃ���A���D�̑傫���͕ω����A���a���قȂ��̕��D�ƂȂ����B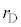 ���������ׂ����������߂�B�������A�C�̂̉��x�͈��ɕۂ���Ă���Ƃ���B
���������ׂ����������߂�B�������A�C�̂̉��x�͈��ɕۂ���Ă���Ƃ���B
(2) �ݖ�V(1)�ŏ\�����Ԃ��o������A�ق��J�����܂܁A��̕��D���̋C�̂̉��x���������킸���ɏグ���B���D�̓����͍����Ȃ������A�Ⴍ�Ȃ������A���R�Ƌ��ɓ�����B�K�v�Ȃ�A�}��p���Ă悢�B
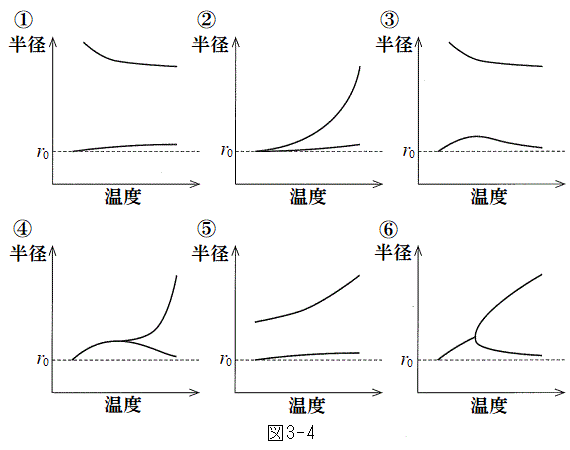 (3) �ݖ�V(2)�ŏ\�����Ԃ��o������A���x�͕��D���̋C�̂̉��x���������Ɖ������B��̕��D�̔��a�����x�̊��Ƃ��Đ}������Ƃ��A�ł��K�Ȃ��̂�}3-4�̇@�`�E�����I�ׁB
(3) �ݖ�V(2)�ŏ\�����Ԃ��o������A���x�͕��D���̋C�̂̉��x���������Ɖ������B��̕��D�̔��a�����x�̊��Ƃ��Đ}������Ƃ��A�ł��K�Ȃ��̂�}3-4�̇@�`�E�����I�ׁB
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�ڐV�����ݒ�̖��ł����A�U�ȍ~�̓J���œ�����ƃE����������܂��B���ɇV�͐F�X�ƔY�ނ��ƂɂȂ�܂��B���͍��C�������C���Ɍ������Đ����A�Ƃ��������ōl���܂��傤�B
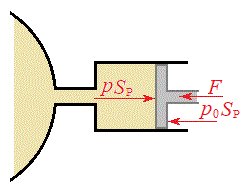 �T(1) �s�X�g���̖ʐς�
�T(1) �s�X�g���̖ʐς�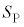 �C�s�X�g���������������̗͂�F�Ƃ��āA�s�X�g���ɂ͑��ɁA�O�C���ɂ�鍶�����̗�
�C�s�X�g���������������̗͂�F�Ƃ��āA�s�X�g���ɂ͑��ɁA�O�C���ɂ�鍶�����̗�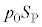 �C�t�̂̈��͂ɂ��E�����̗�
�C�t�̂̈��͂ɂ��E�����̗�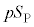 �������܂�(�E�})�B�s�X�g����������艟���̂ŗ͂̂荇�����������A�s�X�g���ɓ����͂̂荇�����A
�������܂�(�E�})�B�s�X�g����������艟���̂ŗ͂̂荇�����������A�s�X�g���ɓ����͂̂荇�����A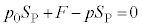 �@��
�@�� 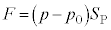
�s�X�g����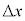 �����Ƃ��A�V�����_�[���̉t�̂̑̐ς̌�����
�����Ƃ��A�V�����_�[���̉t�̂̑̐ς̌�����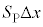 �ł����A����́A���D���̉t�̂̑̐ϑ���
�ł����A����́A���D���̉t�̂̑̐ϑ���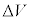 �ɓ������Ȃ�܂��B�s�X�g�������̂ɗv�����d���́A
�ɓ������Ȃ�܂��B�s�X�g�������̂ɗv�����d���́A 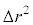 �C
�C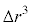 �����āA
�����āA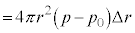 ......[��]�@����@
......[��]�@����@
(2) ���D�̕\�ʐς̕ω�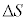 �́A
�́A 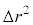 �����āA
�����āA��蕶���̎���p���āA���D�̕\�ʐς�傫������̂ɗv�����d���́A
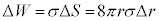 ......[��]�@����A
......[��]�@����A
(3) �s�X�g������ĂȂ����d�����A�S�ĕ��D�̕\�ʐς�傫������̂ɗv����d���ɕϊ������Ƃ��āA�@���A�Ƃ���ƁA
�U(1) ���a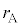 �̕��D���̈��͂�
�̕��D���̈��͂�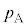 �C���a
�C���a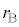 ���̕��D���̈��͂�
���̕��D���̈��͂�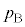 �Ƃ���ƁA�B���A
�Ƃ���ƁA�B���A 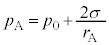 �C
�C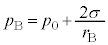 �@����C
�@����C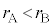 �̏ꍇ�A
�̏ꍇ�A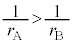 ���A
���A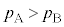 �ł��B����āA�ق��J���ƁA���͂̍������a�̏��������D�����������̔��a�̑傫�����D�̕��ɋC�̂��ڂ�܂��B�@�A ......[�A]�܂�A�B���A���a���������Ȃ�ƕ��D���̈��͂������Ȃ�̂ŁA�[�����Ԃ��o�߂���ƁA���a�̏��������D����傫�����C�̂��ڂ�Â��A���a�̏��������D�͂��ڂ�ł��܂��܂��B�@�C ......[�C]���R�F���a�̏����ȕ��D�̕������D���̈��͂������Ȃ邽�߁B ......[��]
�ł��B����āA�ق��J���ƁA���͂̍������a�̏��������D�����������̔��a�̑傫�����D�̕��ɋC�̂��ڂ�܂��B�@�A ......[�A]�܂�A�B���A���a���������Ȃ�ƕ��D���̈��͂������Ȃ�̂ŁA�[�����Ԃ��o�߂���ƁA���a�̏��������D����傫�����C�̂��ڂ�Â��A���a�̏��������D�͂��ڂ�ł��܂��܂��B�@�C ......[�C]���R�F���a�̏����ȕ��D�̕������D���̈��͂������Ȃ邽�߁B ......[��]
(2) ���D���̋C�̂̉��x�͈��ɕۂ���Ă���̂ŁA���̉��x��T�C�C�̒萔��R�Ƃ��܂��B���a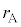 �̕��D����
�̕��D����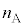 �����̋C�̂�����Ƃ��āA��ԕ������́A
�����̋C�̂�����Ƃ��āA��ԕ������́A 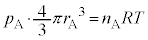 �@����D
�@����D���a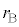 �̕��D����
�̕��D����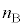 �����̋C�̂�����Ƃ��āA��ԕ������́A
�����̋C�̂�����Ƃ��āA��ԕ������́A 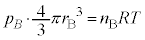 �@����E
�@����E�ŏ����a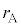 ���������D�͊��S�ɂ��ڂ�ł��܂��̂ŁA�ŏ����a
���������D�͊��S�ɂ��ڂ�ł��܂��̂ŁA�ŏ����a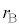 ���������D�̕��ɋC�̂͑S���ڂ��Ă��܂��A���a��
���������D�̕��ɋC�̂͑S���ڂ��Ă��܂��A���a��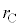 �ɂȂ������D�ɂ�
�ɂȂ������D�ɂ�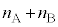 �����̋C�̂�����A����̈��͂�
�����̋C�̂�����A����̈��͂�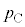 �Ƃ���ƁA��ԕ������́A
�Ƃ���ƁA��ԕ������́A 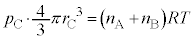 �@����F
�@����F�D�{�E�ƇF���A
�C��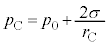 ���A
���A
�V�@���ar�̊��ƂȂ����W���F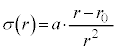 (
(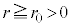 �C
�C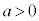 )��p���āA
)��p���āA �C��蔼�ar�̕��D���̈���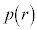 �́A
�́A 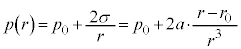 �@����G
�@����G(1) ���ɕۂ���Ă��鉷�x��T�Ƃ��܂��B���ar�̕��D���ɋC�̂�n��������Ƃ��āA�C�̂̏�ԕ������́A
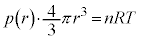 �@����H
�@����H�G���A
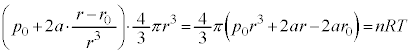
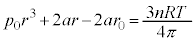 �@����I
�@����I���̍��ӂ�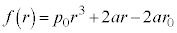 �Ƃ����܂��B
�Ƃ����܂��B
�����ŁA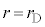 �ߕӂŁA���x���A�܂�A
�ߕӂŁA���x���A�܂�A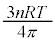 �����̏������Ŕ��ar��2�ʂ�̒l���Ƃ�邩�A�Ƃ������Ƃ����ɂȂ�܂��B
�����̏������Ŕ��ar��2�ʂ�̒l���Ƃ�邩�A�Ƃ������Ƃ����ɂȂ�܂��B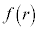 �����������ƁA
�����������ƁA �Ȃ̂ŁA
�܂�A���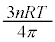 �̒l�ɑ��Ĉ��r�̒l�����Ƃ邱�Ƃ��ł����A����ł́A���a���قȂ��̕��D�������ł��܂���B
�̒l�ɑ��Ĉ��r�̒l�����Ƃ邱�Ƃ��ł����A����ł́A���a���قȂ��̕��D�������ł��܂���B
�����ŁAn���܂߂�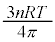 ��̂ň��A�ƍl�����ɁAT���ł����Ă�n�͈قȂ�ƍl���A�ق��J���Ă��ē�̕��D�̈��͂����������Ƃɒ��ڂ��܂��B���DE�ƕ��DF�̔��a���A�قȂ�l�A
��̂ň��A�ƍl�����ɁAT���ł����Ă�n�͈قȂ�ƍl���A�ق��J���Ă��ē�̕��D�̈��͂����������Ƃɒ��ڂ��܂��B���DE�ƕ��DF�̔��a���A�قȂ�l�A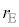 �C
�C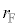 (
(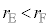 )�������Ƃ��āA����
)�������Ƃ��āA����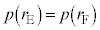 �ł������Ƃ���ƁA���x���ł���AE��F�̒��ɂ���C�̂̃�����
�ł������Ƃ���ƁA���x���ł���AE��F�̒��ɂ���C�̂̃�����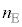 �C
�C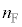 �́A���̑̐ςɔ�Ⴗ��ƍl�����܂�(��ԕ�����
�́A���̑̐ςɔ�Ⴗ��ƍl�����܂�(��ԕ�����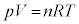 �ɂ�����p��T���Ƃ��Ɉ��ł���AV��n�ɔ�Ⴗ��)�B�܂�A
�ɂ�����p��T���Ƃ��Ɉ��ł���AV��n�ɔ�Ⴗ��)�B�܂�A 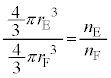 �@����J
�@����J���̂Ƃ��AE���̉��x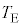 �CF���̉��x
�CF���̉��x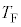 �ɂ��āA��ԕ������A
�ɂ��āA��ԕ������A 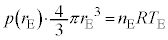 �C
�C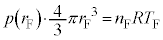 �@����K
�@����K���A
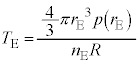 �C
�C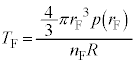 �@����L
�@����L�ƂȂ�܂����A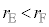 �ł������Ƃ��Ă��A
�ł������Ƃ��Ă��A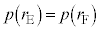 �ł����ćJ����������A
�ł����ćJ����������A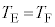 �ɂȂ�܂��B�܂�A���ꉷ�x�Ŕ��a���قȂ��̕��D�������ł��邱�ƂɂȂ�܂��B
�ɂȂ�܂��B�܂�A���ꉷ�x�Ŕ��a���قȂ��̕��D�������ł��邱�ƂɂȂ�܂��B
�����ŁA�G��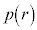 �ɂ��āA�������̈���
�ɂ��āA�������̈���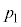 �ɑ��āA
�ɑ��āA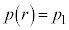 �ƂȂ�r��2�ʂ���邩�A���ׂ܂��B
�ƂȂ�r��2�ʂ���邩�A���ׂ܂��B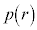 �����������ƁA
�����������ƁA 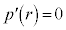 �Ƃ���ƁA
�Ƃ���ƁA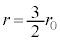 �C
�C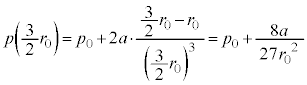
������A�����\�́A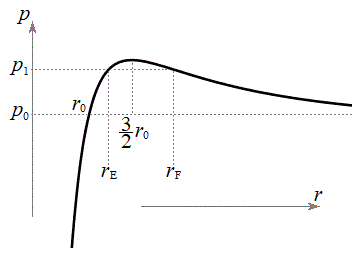 �����\��
�����\��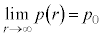 ���A
���A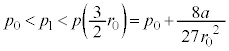 ����
����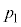 �ɑ���
�ɑ���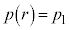 �ƂȂ�r�́A�E�}�̂悤��2�ʂ�̒l
�ƂȂ�r�́A�E�}�̂悤��2�ʂ�̒l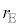 �C
�C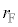 ���Ƃ�܂��B�A���A
���Ƃ�܂��B�A���A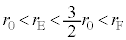 �@����M
�@����M������A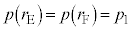 �ł����āA
�ł����āA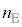 �F
�F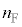 =
= 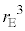 �F
�F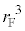 �ł���A�L���
�ł���A�L���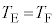 �ƂȂ�܂��B
�ƂȂ�܂��B
�ŏ���̕��D���ǂ�������a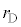 �ŁA�Е����킸���ɂ��ڂ܂��Ĕ��a��
�ŁA�Е����킸���ɂ��ڂ܂��Ĕ��a��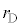 ���������������Ƃ��āA�U(1)�Ɠ����悤�ɍl���Ă݂܂��B��L�̑����\���A
���������������Ƃ��āA�U(1)�Ɠ����悤�ɍl���Ă݂܂��B��L�̑����\���A 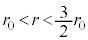 �ɂ�����
�ɂ�����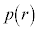 ��r�̑������ł���A
��r�̑������ł���A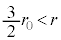 �ɂ�����
�ɂ�����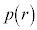 ��r�̌������ł���@���(����)
��r�̌������ł���@���(����)
(2) �C�̂̉��x��T�Ƃ��܂��B���������DE�C�傫�����DF�ɂ��āA���ꂼ�ꔼ�a��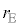 �C
�C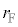 �C�C�̂̃�������
�C�C�̂̃�������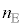 �C
�C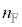 �Ƃ��āA���D���̋C�̂̏�ԕ������́A�K�ŗ^�����܂��B�K��
�Ƃ��āA���D���̋C�̂̏�ԕ������́A�K�ŗ^�����܂��B�K��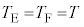 �Ƃ���2����ӁX�������킹�A
�Ƃ���2����ӁX�������킹�A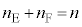 �Ƃ���ƁAn�͈��ŁA
�Ƃ���ƁAn�͈��ŁA 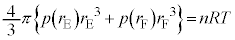 �@����N
�@����N�܂��A�G���A
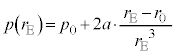 �C
�C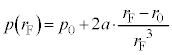 �@����O
�@����O������N�ɑ������ƁA
�܂�����A�ق��J���Ă���̂ŁA���҂̈��͂ɂ��āA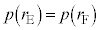 �ł���A�N���A
�ł���A�N���A ������Đ�������ƁA
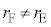 ���A
���A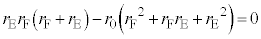 �@����Q
�@����Q�����Q�̂��ƂɁA�P��T�傳�����Ƃ��ɁA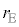 �C
�C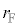 ���ǂ��Ȃ邩�ׁA
���ǂ��Ȃ邩�ׁA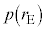 �C
�C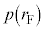 ���ǂ��Ȃ邩���l����悢�̂ł����A���Z�͈̔͂ł͍���ŁA�Ïʂɏ��グ�܂��B
���ǂ��Ȃ邩���l����悢�̂ł����A���Z�͈̔͂ł͍���ŁA�Ïʂɏ��グ�܂��B
�����ŁA�����I�ɏ�������̂͒��߁A�萫�I�ɍl�@���邱�Ƃɂ��܂��B
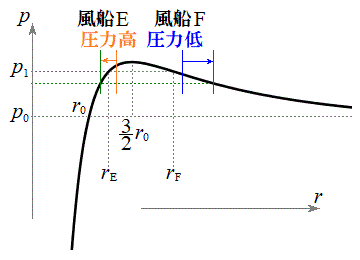 ���xT���㏸����Ƃ��A�I��
���xT���㏸����Ƃ��A�I��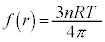 �ɂ����āA��L(��)���
�ɂ����āA��L(��)���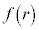 ��r�̒P���������ł��邱�Ƃ���A�I����r���傫���Ȃ�܂��B�]���āA
��r�̒P���������ł��邱�Ƃ���A�I����r���傫���Ȃ�܂��B�]���āA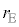 ��
��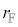 ���傫���Ȃ낤�Ƃ��܂��B�E�}�ɂ����āA�M���A
���傫���Ȃ낤�Ƃ��܂��B�E�}�ɂ����āA�M���A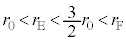 �Ȃ̂ŁA��L��(����)���A���DE���̈��͂͑傫��(�E�}���)�A���DF���̈��͂͏�����(�E�}��)�Ȃ낤�Ƃ��܂��B����ƁA���DE���̈��͂����DF���̈��͂����傫���Ȃ낤�Ƃ���̂ŁA���DE���畗�DF�ɋC�̂��ړ����n�߂܂��B���̌��ʁA���DE�̔��a�͏������Ȃ�A���DF�̔��a�͑傫���Ȃ�܂��B�Ƃ������Ƃ́A�E�}���A���DF���̋C���͉�����A�Ƃ������Ƃł���A�ق��J���Ă���̂ŁA��̕��D�̓����͒Ⴍ�Ȃ�Ƃ������Ƃł��B
�Ȃ̂ŁA��L��(����)���A���DE���̈��͂͑傫��(�E�}���)�A���DF���̈��͂͏�����(�E�}��)�Ȃ낤�Ƃ��܂��B����ƁA���DE���̈��͂����DF���̈��͂����傫���Ȃ낤�Ƃ���̂ŁA���DE���畗�DF�ɋC�̂��ړ����n�߂܂��B���̌��ʁA���DE�̔��a�͏������Ȃ�A���DF�̔��a�͑傫���Ȃ�܂��B�Ƃ������Ƃ́A�E�}���A���DF���̋C���͉�����A�Ƃ������Ƃł���A�ق��J���Ă���̂ŁA��̕��D�̓����͒Ⴍ�Ȃ�Ƃ������Ƃł��B
�Ⴍ�Ȃ��� ......[��]�@���R�F���x���グ��ƁA��̕��D�̔��a���傫���Ȃ�A���������D���̈��͂͑��債�悤�Ƃ��A�傫�����D���̈��͂͌������悤�Ƃ��A���������D����傫�����D�ɋC�̂��ړ�����B�傫�����D�̔��a��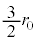 ���傫���A�傫�����D�̔��a���傫���Ȃ�ƁA���D���̋C���͒Ⴍ�Ȃ�B ......[��]
���傫���A�傫�����D�̔��a���傫���Ȃ�ƁA���D���̋C���͒Ⴍ�Ȃ�B ......[��]
(3) (2)�Ƌt�ɍl����ƁA���x��������Ε��D���̈��͍͂����Ȃ�܂��B��L(����)�ɂ��ƁA��̕��D�̔��a�́A�����������傫���Ȃ�A�傫�������������Ȃ�A�₪�āA���҂Ƃ�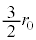 �ɂȂ����Ƃ���ŁA��̕��D�̔��a�͓������Ȃ�܂��B����ɉ��x��������ƁA�I��
�ɂȂ����Ƃ���ŁA��̕��D�̔��a�͓������Ȃ�܂��B����ɉ��x��������ƁA�I��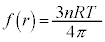 �ɂ����āA(��)���
�ɂ����āA(��)���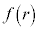 ��r�̒P���������ł��邱�Ƃ���AT����������A�I����r���������A�₪��
��r�̒P���������ł��邱�Ƃ���AT����������A�I����r���������A�₪��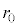 �ɂȂ�܂��B�����Ȃ��Ă���O���t�́A�E ......[��]
�ɂȂ�܂��B�����Ȃ��Ă���O���t�́A�E ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 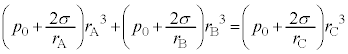
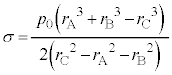 ......[��]
......[��]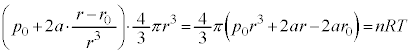
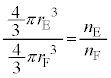 �@����J
�@����J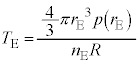 �C
�C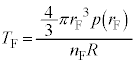 �@����L
�@����L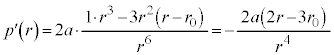
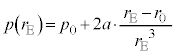 �C
�C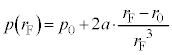 �@����O
�@����O