���啨��'23�N�O��[1]
���̕��͂�ǂ�ŁA�@�@�ɓK�������܂��͐��l���A���ꂼ��̉��ɋL������B�Ȃ��A�@�@�͂��ł��@�@�ŗ^����ꂽ���̂Ɠ������̂�\���B�܂��A��1�C��2�ł́A�w���ɂ��������āA�����ꂼ��̉��ɋL������B�������A�~������π�Ƃ���B
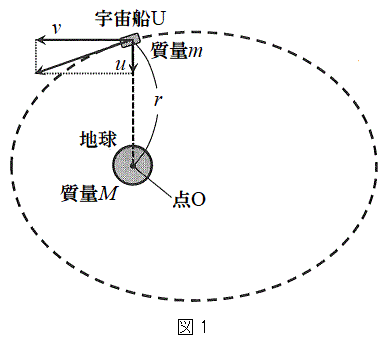 (1) �}1�̂悤�ɓ_O�𒆐S�Ƃ��鎿��M�̒n���̂܂����A�n�����\������������m�̉F���DU���ȉ~�O���ł܂���Ă���B�F���DU����_O�Ɍ����������̑�����u�C����Ɛ����ȕ����̑�����v�C�F���DU�Ɠ_O�Ԃ̋�����r�Ƃ��A�F���DU�ɂ͓_O�Ɍ����������̖��L���݂͂̂��͂��炭���̂Ƃ���B���̂Ƃ��A�F���DU�̉^���G�l���M�[��m�Cu�Cv�ŕ\�����@�A�@�ł���A����ɁA�ʒu�G�l���M�[�͖���������0�Ƃ��Ė��L���͒萔G�����M�Cm�Cr�ŕ\�����@�C�@�ł���B�F���DU�̗͊w�I�G�l���M�[�̈��lE�Ƃ����
(1) �}1�̂悤�ɓ_O�𒆐S�Ƃ��鎿��M�̒n���̂܂����A�n�����\������������m�̉F���DU���ȉ~�O���ł܂���Ă���B�F���DU����_O�Ɍ����������̑�����u�C����Ɛ����ȕ����̑�����v�C�F���DU�Ɠ_O�Ԃ̋�����r�Ƃ��A�F���DU�ɂ͓_O�Ɍ����������̖��L���݂͂̂��͂��炭���̂Ƃ���B���̂Ƃ��A�F���DU�̉^���G�l���M�[��m�Cu�Cv�ŕ\�����@�A�@�ł���A����ɁA�ʒu�G�l���M�[�͖���������0�Ƃ��Ė��L���͒萔G�����M�Cm�Cr�ŕ\�����@�C�@�ł���B�F���DU�̗͊w�I�G�l���M�[�̈��lE�Ƃ�����ƕ\�����Ƃ��ł���B�����ŁA�P�v���[�̑�2�@��(�ʐϑ��x���̖@��)�����藧���Ƃ���ʐϑ��x�����̒l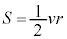 �Ƃ��āAr���܂ލ����܂Ƃ߂���
�Ƃ��āAr���܂ލ����܂Ƃ߂���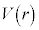 ��G�CM�Cm�Cr�CS��p���ĕ\�����@�E�@�ł���B�F���DU���ȉ~�O�����^������ԁA
��G�CM�Cm�Cr�CS��p���ĕ\�����@�E�@�ł���B�F���DU���ȉ~�O�����^������ԁA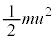 ��0���ŏ��l�Ƃ���L���͈̔͂�ω�����B���������āA
��0���ŏ��l�Ƃ���L���͈̔͂�ω�����B���������āA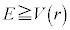 �ƂȂ�r�͈̔͂��A�F���DU�Ɠ_O�Ԃ̋������ω�����͈͂�\���B
�ƂȂ�r�͈̔͂��A�F���DU�Ɠ_O�Ԃ̋������ω�����͈͂�\���B
��1�@��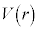 �̊T�`�͂ǂ̂悤�ɂȂ邩�Br�������C
�̊T�`�͂ǂ̂悤�ɂȂ邩�Br�������C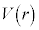 ���c���Ƃ��ē���
���c���Ƃ��ē���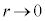 ��
��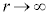 �̂Ƃ��̐U�镑�����킩��悤�ɃO���t�ɕ`���B���̂Ƃ��A�n����傫���������ł��鎿��M�̎��_�Ƃ݂Ȃ��B�܂��A�����A�c����0�ȊO�̒l���L������K�v�͂Ȃ��B
�̂Ƃ��̐U�镑�����킩��悤�ɃO���t�ɕ`���B���̂Ƃ��A�n����傫���������ł��鎿��M�̎��_�Ƃ݂Ȃ��B�܂��A�����A�c����0�ȊO�̒l���L������K�v�͂Ȃ��B
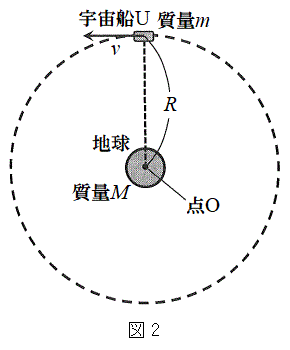 (2) �}2�̂悤�ɁA�F���DU�̋O�������aR�̉~�O���Ƃ݂Ȃ���ꍇ���l����B����R�͈ȉ��ŏ�Ɉ��l���Ƃ�A���������āA(1)��r�ƈقȂ邱�Ƃɒ��ӂ���B���̂Ƃ��A�F���DU�̑�����v�C�O����������������T�Ƃ���B����T��G�CM�CR�ŕ\�����@�G�@�ł���B
(2) �}2�̂悤�ɁA�F���DU�̋O�������aR�̉~�O���Ƃ݂Ȃ���ꍇ���l����B����R�͈ȉ��ŏ�Ɉ��l���Ƃ�A���������āA(1)��r�ƈقȂ邱�Ƃɒ��ӂ���B���̂Ƃ��A�F���DU�̑�����v�C�O����������������T�Ƃ���B����T��G�CM�CR�ŕ\�����@�G�@�ł���B���ɁA�F���DU�ɁA�_O�Ɍ���������(���a����)�ɏ\���ア�͂��O������u�ԓI�ɉ�������ꍇ���l����B����ƁA�F���DU�͌��̉~�O���Ƃ͂킸���ɈقȂ�O�������ǂ�n�߂�B���̌�̉^�����ȉ��̂悤�ɍl�@���悤�B�F���DU�̔��a�����̈ʒu���������𐳂Ƃ���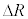 ���������ɂ��ꂽ�_�A���Ȃ킿�_O���狗��
���������ɂ��ꂽ�_�A���Ȃ킿�_O���狗��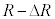 �̓_�ł́A���a�����ɐ����ȕ����̑�����
�̓_�ł́A���a�����ɐ����ȕ����̑�����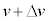 �Ƃ��A
�Ƃ��A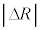 ��
��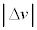 �͂��ꂼ��R��v�ɔ��ɏ\���������Ƃ���B�u�ԓI�ȊO�͂ɂ��F���DU�̉^���G�l���M�[�͂킸���ɑ������邪�A���a�����̗͂ł��邽�߃P�v���[�̑�2�@���͂��̊ԁA��ɐ�������B������A
�͂��ꂼ��R��v�ɔ��ɏ\���������Ƃ���B�u�ԓI�ȊO�͂ɂ��F���DU�̉^���G�l���M�[�͂킸���ɑ������邪�A���a�����̗͂ł��邽�߃P�v���[�̑�2�@���͂��̊ԁA��ɐ�������B������A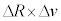 �ɔ�Ⴗ�鍀������ƁAR�C
�ɔ�Ⴗ�鍀������ƁAR�C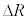 �Cv��p����
�Cv��p����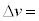 �@�I�@�ƕ\����B
�@�I�@�ƕ\����B
�ʒu�����̉~�O���̔��aR����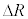 ���������ɂ��ꂽ���ƂŁA�F���DU�ɂ͂��炭�͂��ǂ̂悤�ɕω����邩���߂悤�B�ȉ��ł́A
���������ɂ��ꂽ���ƂŁA�F���DU�ɂ͂��炭�͂��ǂ̂悤�ɕω����邩���߂悤�B�ȉ��ł́A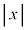 �C
�C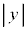 ��1���\���������Ƃ��ɐ��藧�ߎ���
��1���\���������Ƃ��ɐ��藧�ߎ���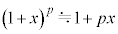 �C
�C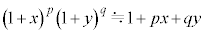 (p�Cq�͎���)��p����B�܂��A���L���͂̑傫���̑�����
(p�Cq�͎���)��p����B�܂��A���L���͂̑傫���̑�����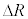 �ɔ�Ⴗ��`��G�CM�Cm�CR��p���ĕ\����
�ɔ�Ⴗ��`��G�CM�Cm�CR��p���ĕ\���� 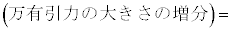 �@�J�@
�@�J�@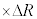
�ł���B����A���S�͔͂��a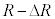 �C����
�C����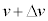 �̉~�^���Ɠ��l�ɍl���邱�Ƃ��ł���B������A���S�͂̑傫���̑�����
�̉~�^���Ɠ��l�ɍl���邱�Ƃ��ł���B������A���S�͂̑傫���̑�����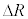 �ɔ�Ⴗ��`��m�CR�Cv��p���ĕ\����
�ɔ�Ⴗ��`��m�CR�Cv��p���ĕ\���� 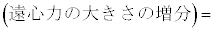 �@�L�@
�@�L�@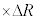
�ł���B�ȏ���A�������𐳂Ƃ��鍇�͂̑�����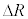 �ɔ�Ⴗ��`��G�CM�Cm�CR��p����
�ɔ�Ⴗ��`��G�CM�Cm�CR��p���� 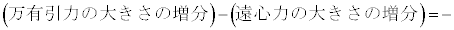 �@�N�@
�@�N�@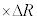
�Ƌ��܂�B���������āA���̗͉͂F���DU�̔��a�����̈ʒu�̂�������ɖ߂������͂Ƃ��Ă͂��炭�B���̗͂������N���������x��������𐳂Ƃ���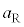 �ƒ�`����ƁA���a�����̉^����������
�ƒ�`����ƁA���a�����̉^����������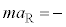 �@�N�@
�@�N�@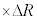 �ƂȂ�B�ȏ�̋c�_��
�ƂȂ�B�ȏ�̋c�_��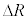 �����A�܂�F���DU�̈ʒu�����aR����O���ɂ��ꂽ�ꍇ�ɂ���������B����āA��L�̉^������������F���DU�͔��a�����̔����ψ�
�����A�܂�F���DU�̈ʒu�����aR����O���ɂ��ꂽ�ꍇ�ɂ���������B����āA��L�̉^������������F���DU�͔��a�����̔����ψ�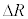 �ɂ��ĒP�U�����邱�Ƃ��킩��B���̔����ȐU���^���̎�����t �Ƃ���ƁA�F���DU���O��������������T�Ƃ̔�
�ɂ��ĒP�U�����邱�Ƃ��킩��B���̔����ȐU���^���̎�����t �Ƃ���ƁA�F���DU���O��������������T�Ƃ̔�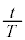 ���@�P�@�ł���B���̉^���͌��̉~�^���Ƃ͈قȂ���̂́A�F���DU�����̌���p�����Ēn�����������邱�Ƃ͕ς��Ȃ��B
���@�P�@�ł���B���̉^���͌��̉~�^���Ƃ͈قȂ���̂́A�F���DU�����̌���p�����Ēn�����������邱�Ƃ͕ς��Ȃ��B
(3) ����m�̉F���DU������M�̓V��X�̂܂����^������ꍇ���l����Bm��M���\���������Ƃ���B�F���DU�ɂ͓V��X����̈��݂͂̂��͂��炭���A���̗͂̑傫���̓j���[�g���̖��L���̖͂@�����܂ވ�ʓI�Ȍ`�ŁA
�ƕ\����Ƃ���B�����ŁAr�͓V��X�̒��S����F���DU�܂ł̋����AA��k�͐��̒萔�ł���A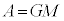 �C
�C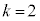 �Ȃ�j���[�g���̖��L���̖͂@���ɑ�������B�Ȃ��ȉ��ł́A�V��X����̈��͈ȊO�̕����@���A���Ȃ킿���S�͂�\�����ƃP�v���[�̑�2�@���͕ς�炸���藧���̂Ƃ���B
�Ȃ�j���[�g���̖��L���̖͂@���ɑ�������B�Ȃ��ȉ��ł́A�V��X����̈��͈ȊO�̕����@���A���Ȃ킿���S�͂�\�����ƃP�v���[�̑�2�@���͕ς�炸���藧���̂Ƃ���B
���܁A�C�ӂ�k�̏ꍇ�ɑ��āA���̈��͂����S�͂Ƃ���A�V��X�̒��S�����锼�aR�̉~�^�����l���邱�Ƃ��ł���B���̂Ƃ��̔��a�����ɐ����ȕ����̑�����A�CR�Ck�ŕ\�����@�R�@�ł���B�����ŁA�F���DU�ɁA�V��X�̒��S�Ɍ����������ɏ\���ア�͂��O������u�ԓI�ɉ�������ꍇ���l�@���悤�B(2)�Ɠ��l�ɁA�F���DU�̋O�����킸���ɓ������ɕω������Ƃ���D�F���DU�̋O���̂��ꂪ�������𐳂Ƃ���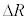 �̏ꍇ�A���͂̑�����(2)�Ɠ��l�̕��@�ōl���邱�Ƃ��ł���B���͂̑傫����\������
�̏ꍇ�A���͂̑�����(2)�Ɠ��l�̕��@�ōl���邱�Ƃ��ł���B���͂̑傫����\������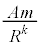 �ƂȂ������Ƃɒ��ӂ��A���̑�����
�ƂȂ������Ƃɒ��ӂ��A���̑�����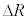 �ɔ�Ⴗ��`��A�Cm�CR�Ck��p���ĕ\����
�ɔ�Ⴗ��`��A�Cm�CR�Ck��p���ĕ\���� 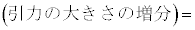 �@�T�@
�@�T�@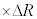
�ł���B�������𐳂Ƃ��鍇�͂̑�����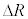 �ɔ�Ⴗ��`��A�Cm�CR�Ck��p����
�ɔ�Ⴗ��`��A�Cm�CR�Ck��p���� 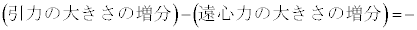 �@�V�@
�@�V�@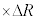
�Ƌ��܂�B�ȏ�̋c�_��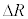 �����A�܂�F���DU�̈ʒu�����aR����O���ɂ��ꂽ�ꍇ�ɂ���������B
�����A�܂�F���DU�̈ʒu�����aR����O���ɂ��ꂽ�ꍇ�ɂ���������B
������A�F���DU�̉^����k�̒l�ɉ����ĈقȂ邱�Ƃ��ȉ��̂悤�ɂ킩��B�܂��A(2)�ōl�����悤�Ȕ��a�����̔����U�����^���ƂȂ�̂�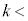 �@�X�@�̏ꍇ�݂̂ł���B�܂��A���̏ꍇ�A�����ȐU���̎���
�@�X�@�̏ꍇ�݂̂ł���B�܂��A���̏ꍇ�A�����ȐU���̎���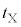 �ƋO��������������
�ƋO��������������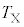 �̔�
�̔�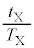 ��k�݂̂̊��Ƃ����@�Z�@�ƕ\����B
��k�݂̂̊��Ƃ����@�Z�@�ƕ\����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�Ō�ŋt2�摥����O�ꂽ�z�肪�o�ꂵ�܂����A���L���͂Ɋւ�����ł��B
����āA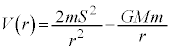 ......[�E]
......[�E]
����āA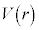 ��
��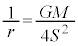 �C�܂�A
�C�܂�A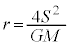 �̂Ƃ��ɍŏ��ƂȂ�܂�(2�����̍ő�E�ŏ����Q��)�B
�̂Ƃ��ɍŏ��ƂȂ�܂�(2�����̍ő�E�ŏ����Q��)�B
����āA��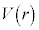 �̃O���t�̊T�`�͉E�}�B
�̃O���t�̊T�`�͉E�}�B
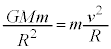 �@��
�@�� 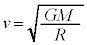 �@����A
�@����A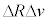 ������ƁA
������ƁA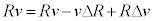 �@��
�@�� 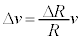 (
(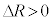 ��
��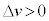 �ł�)�@����B�@
�ł�)�@����B�@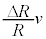 ......[�I]
......[�I]���L���͂̕ω��́A��蕶���̋ߎ�����p���āA
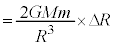 (���̒l�Ȃ̂ŁA�傫���̑����ł�)�@
(���̒l�Ȃ̂ŁA�傫���̑����ł�)�@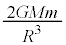 ......[�J]
......[�J]���S���̕ω��́A��蕶���̋ߎ����ƇB��p����ƁA 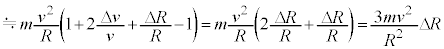 (���̒l�Ȃ̂ŁA�傫���̑����ł�)�@
(���̒l�Ȃ̂ŁA�傫���̑����ł�)�@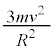 ......[�L]
......[�L][�L]�̌��ʁA�܂艓�S�͂̑傫���̑����́A�A��p���ď��������ƁA
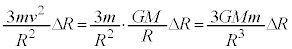 �@����C
�@����C���L���͂̑傫���̑������牓�S�͂̑傫���̑��������������̂́A[�J]�̌��ʂ���C�������āA
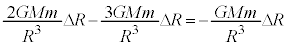 �@
�@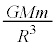 ......[�N]
......[�N]�P�U���̌����F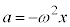 ���A�P�U���̊p�U������ω�Ƃ���ƁA
���A�P�U���̊p�U������ω�Ƃ���ƁA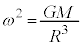
�P�U���̎���t �́A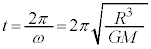 �C[�G]���
�C[�G]���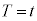 �Ȃ̂ŁA
�Ȃ̂ŁA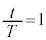 ......[�P]
......[�P]
(3) ����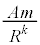 ���ĉ~�^������F���DU�̉^���������́A�F���DU�̔��a�����ɐ����ȕ����̑�����
���ĉ~�^������F���DU�̉^���������́A�F���DU�̔��a�����ɐ����ȕ����̑�����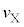 �Ƃ��āA�F���DU�̉^���������́A
�Ƃ��āA�F���DU�̉^���������́A 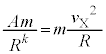 �@��
�@�� 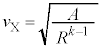 ......[�R]�@����D
......[�R]�@����D���͂̕ω��́A
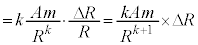 (���̒l�Ȃ̂ő傫���̑����ł�)�@
(���̒l�Ȃ̂ő傫���̑����ł�)�@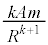 ......[�T]
......[�T]���S�͂̕ω��́A�B��[�R]�̌��ʂ�p���āA
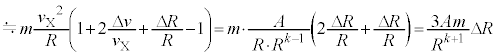 �@����E
�@����E���͂̑傫���̑������牓�S�͂̑傫���̑��������������̂́A[�T]�̌��ʂ���E�������āA
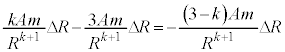 �@
�@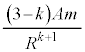 ......[�V]
......[�V]�F���DU�̉^�������a�����̔����U�����^���ɂȂ�̂́A[�V]�������͂ƂȂ�Ƃ��ŁA���̏����́A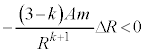 �@��
�@�� 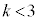 �@3.......[�X]�~�^���̎���
�@3.......[�X]�~�^���̎���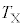 �͇D���A
�͇D���A 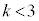 �̂Ƃ��A�P�U���̉^���������́A�����x��
�̂Ƃ��A�P�U���̉^���������́A�����x��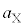 �Ƃ��āA[�V]�̌��ʂ�p���āA
�Ƃ��āA[�V]�̌��ʂ�p���āA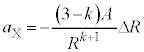 ���A�p�U����
���A�p�U����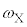 �́A
�́A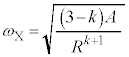 �C�P�U���̎���
�C�P�U���̎���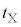 �́A
�́A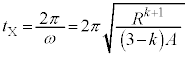 �C����āA
�C����āA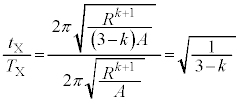 ......[�Z]
......[�Z]
��2�@ �̂Ƃ��A[�V]�̗͕͂����͂ƂȂ炸�A���͂̑����́A�V��X�̕����������A���̑傫���́A
�̂Ƃ��A[�V]�̗͕͂����͂ƂȂ炸�A���͂̑����́A�V��X�̕����������A���̑傫���́A �̏ꍇ�A[�V]�̌��ʂɂ��
�̏ꍇ�A[�V]�̌��ʂɂ�� �ɔ�Ⴕ�đ��債�܂��B�F���DU�̉~�^���̔��a���������Ȃ��čs���܂��B
�ɔ�Ⴕ�đ��債�܂��B�F���DU�̉~�^���̔��a���������Ȃ��čs���܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 

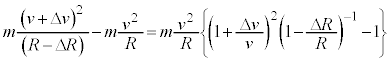
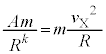 �@��
�@�� 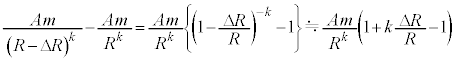
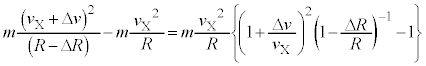
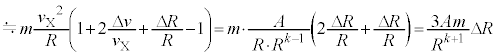 �@����E
�@����E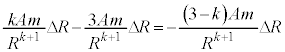 �@
�@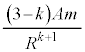 ......[�V]
......[�V]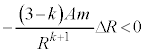 �@��
�@�� 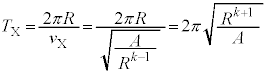
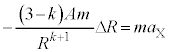
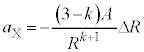 ���A�p�U����
���A�p�U����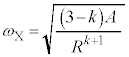 �C�P�U���̎���
�C�P�U���̎���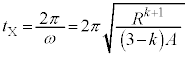 �C����āA
�C����āA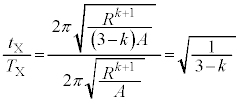 ......[�Z]
......[�Z]