���s��w2024�N�O�������������
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
[1]�@���̕��͂�ǂ�ŁA�@�@�ɓK�������܂��͐��l���A���ꂼ��̉��ɋL������B�Ȃ��A�@�@�͂��ł��@�@�ŗ^����ꂽ���̂Ɠ������̂�\���B�܂��A��1�C��2�ł́A�w���ɂ��������āA�����ꂼ��̉��ɋL������B�������A�~������π�C�d�͉����x��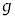 �Ƃ���B��C�̒�R�͖����ł�����̂Ƃ���B
�Ƃ���B��C�̒�R�͖����ł�����̂Ƃ���B
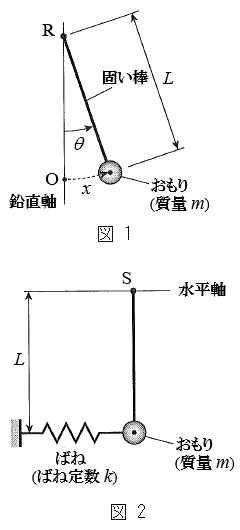 (1) �}1�̂悤�ɁA���ʂ������ł���ł��_�̉��[�ɁA���ʂ�m�ŏ��������`�̂���������t�����U��q�ɂ��čl����B�_�͏�[�̌Œ�_R���x�_�Ƃ��āAR���܂މ����ʓ������炩�ɉ�]����B�Œ�_���炨����̏d�S(�_�̉��[)�܂ł̋�����L�C�~���ɉ������ʼn��_O����̂�����̕ψʂ�x(�E������)�A����������̖_�̉�]�p��θ(�����v���𐳁A�P�ʂ̓��W�A��)�Ƃ���B
(1) �}1�̂悤�ɁA���ʂ������ł���ł��_�̉��[�ɁA���ʂ�m�ŏ��������`�̂���������t�����U��q�ɂ��čl����B�_�͏�[�̌Œ�_R���x�_�Ƃ��āAR���܂މ����ʓ������炩�ɉ�]����B�Œ�_���炨����̏d�S(�_�̉��[)�܂ł̋�����L�C�~���ɉ������ʼn��_O����̂�����̕ψʂ�x(�E������)�A����������̖_�̉�]�p��θ(�����v���𐳁A�P�ʂ̓��W�A��)�Ƃ���B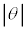 �͏\���ɏ������A�Ƃ��ɂ��Ƃ��̂Ȃ�����
�͏\���ɏ������A�Ƃ��ɂ��Ƃ��̂Ȃ�����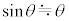 �C
�C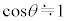 �Ƌߎ�����B
�Ƌߎ�����B������̉~�������̉����x��a(�E������)�Ƃ���Ƃ��A������̉~�������̉^����������a�Cm�CL�C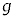 �Cx��p����
�Cx��p���� 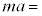 �@�A�@
�@�A�@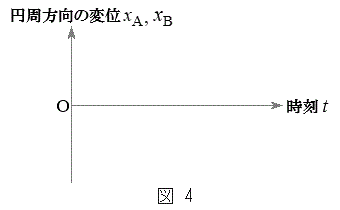 ��1�@�}3�̈ʒu���炨����B�݂̂��E�����Ɏ����グ�ĐÂ��ɗ����A����
��1�@�}3�̈ʒu���炨����B�݂̂��E�����Ɏ����グ�ĐÂ��ɗ����A����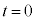 �ɂ����č������ɑ���
�ɂ����č������ɑ���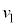 �ł�����A�ɏՓ˂������B
�ł�����A�ɏՓ˂������B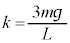 �̊W�����藧�Ƃ��A�}4�����ɕ`���ʂ��āA2�̂����肪
�̊W�����藧�Ƃ��A�}4�����ɕ`���ʂ��āA2�̂����肪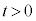 ��3��Փ˂���܂ł̂�����A�CB�̉~�������̕ψ�
��3��Փ˂���܂ł̂�����A�CB�̉~�������̕ψ�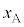 �C
�C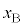 �Ǝ���t�̊W���A���ꂼ���������ѓ_���ŕ`���B�O���t�ɂ́A���ꂼ��̂�����̕ψʂ̐U���Ƃ����肪�Փ˂��鎞�����Ak��p�����Ɏ����B�����̓��o�ߒ����L�q����B
�Ǝ���t�̊W���A���ꂼ���������ѓ_���ŕ`���B�O���t�ɂ́A���ꂼ��̂�����̕ψʂ̐U���Ƃ����肪�Փ˂��鎞�����Ak��p�����Ɏ����B�����̓��o�ߒ����L�q����B
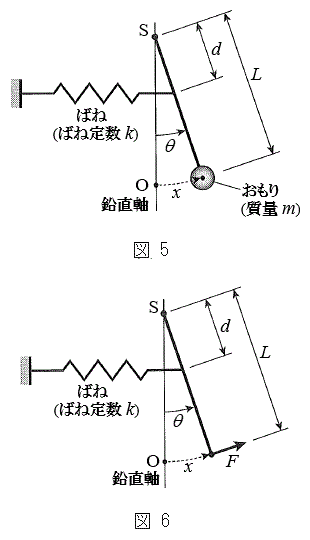 �}2�̐U��q�ɂ����āA�}5�̂悤�ɁA�˂̈ʒu���Œ�_S���狗��d�̈ʒu�ɕύX�����B������̉~�������̕ψʂ�x�̂Ƃ��A�˂̐L�т��@�J�@�ł���B
�}2�̐U��q�ɂ����āA�}5�̂悤�ɁA�˂̈ʒu���Œ�_S���狗��d�̈ʒu�ɕύX�����B������̉~�������̕ψʂ�x�̂Ƃ��A�˂̐L�т��@�J�@�ł���B
�����ŁA������ɂ͂��炭�͂𗝉����邽�߁A�U��q�̉^�����ɂ�����Ɩ_�̊Ԃɂ͂��炭�͂��l����B�}6�̂悤�ɁA�����肩��_�̉��[�ɍ�p����͂̉~������������F(�E������)�Ƃ���B�˂Ɩ_�̎��ʂ͖����ł��邽�߁A�_�ɂ͂��炭�͂̓_S�܂��̃��[�����g�̂肠�����A�Î~���Ă���Ƃ��Ɠ��l�ɐ��藧�B���������āAF��L�Cd�Ck�Cx��p����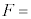 �@�L�@�ƕ\����B�}5�̂˕t���U��q�ɂ����āA�_���炨����ɂ͐}6��F�̔���p���͂��炫�A������̉~�������̉^���������͎��̂悤�ɕ\�����Ƃ��ł���B
�@�L�@�ƕ\����B�}5�̂˕t���U��q�ɂ����āA�_���炨����ɂ͐}6��F�̔���p���͂��炫�A������̉~�������̉^���������͎��̂悤�ɕ\�����Ƃ��ł���B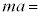 �@�A�@�|F
�@�A�@�|F���̂˕t���U��q�͒P�U�����A���̊p�U�������@�N�@�ł���B
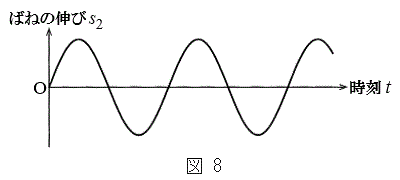
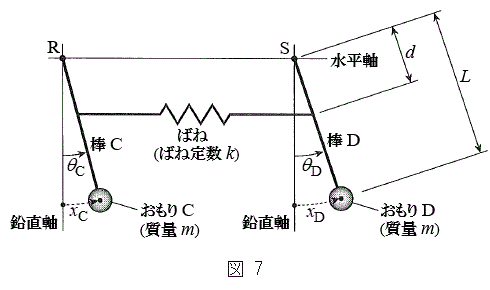 (2) �}7�̂悤�ɁA�}1�̐U��q2�����ꂼ��Œ�_R�CS�Ŏx�����A���ʂ������ł���˂��A�Œ�_���狗��d�̈ʒu�Ɏ��t�����B�˂͏\���ɒ����A�˂��X�����Ƃɂ��A�˂̐L�сA����ѕ����͂̑傫���ƕ����ւ̉e���͖����ł���B�˒萔��k�Ƃ��A�˂́A�_C�CD�̉�]�p
(2) �}7�̂悤�ɁA�}1�̐U��q2�����ꂼ��Œ�_R�CS�Ŏx�����A���ʂ������ł���˂��A�Œ�_���狗��d�̈ʒu�Ɏ��t�����B�˂͏\���ɒ����A�˂��X�����Ƃɂ��A�˂̐L�сA����ѕ����͂̑傫���ƕ����ւ̉e���͖����ł���B�˒萔��k�Ƃ��A�˂́A�_C�CD�̉�]�p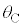 �C
�C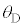 ���Ƃ���0�̂Ƃ����R���ł���B
���Ƃ���0�̂Ƃ����R���ł���B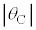 �C
�C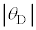 �͏\���ɏ������A
�͏\���ɏ������A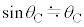 �C
�C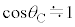 �C
�C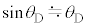 �C
�C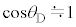 �Ƌߎ�����B
�Ƌߎ�����B������C�CD�̍ʼn��_����̉~���ɉ������ψʂ�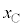 �C
�C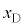 (�E������)�Ƃ���ƁA�˂̐L��
(�E������)�Ƃ���ƁA�˂̐L��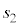 ���@�P�@�ƕ\����B������C�CD�̉~�������̉����x��
���@�P�@�ƕ\����B������C�CD�̉~�������̉����x��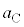 �C
�C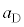 (�E������)�Ƃ���ƁA������C�CD�̉~�������̉^���������́A
(�E������)�Ƃ���ƁA������C�CD�̉~�������̉^���������́A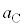 �C
�C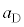 �Cm�CL�C
�Cm�CL�C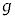 �Cd�Ck�C
�Cd�Ck�C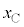 �C
�C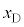 ��p���Ď����ŕ\�����B
��p���Ď����ŕ\�����B 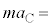 �@�R�@
�@�R�@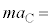 �@�T�@
�@�T�@2�̐U��q�������p�U����ω�ŒP�U��������ʂȏ�Ԃ��l����Ƃ��A���������藧�B
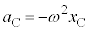 �C
�C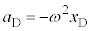
�㎮���^���������ɑ�����A
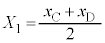 �C
�C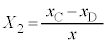
 ��2�@��ʂɂ́A�}7�̂�����C�CD�̕ψ�
��2�@��ʂɂ́A�}7�̂�����C�CD�̕ψ�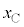 �C
�C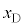 �́A��L�ōl����2��ނ̒P�U���̏d�ˍ��킹�ŕ\�����Ƃ��ł���B�����ł�
�́A��L�ōl����2��ނ̒P�U���̏d�ˍ��킹�ŕ\�����Ƃ��ł���B�����ł�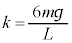 �̊W�����藧�ꍇ���l����B
�̊W�����藧�ꍇ���l����B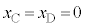 �ŐÎ~���Ă��邨����C�CD�ɑ��āA����
�ŐÎ~���Ă��邨����C�CD�ɑ��āA����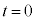 �ɂ����Ă�����D�݂̂ɉE���������x
�ɂ����Ă�����D�݂̂ɉE���������x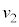 ��^�����Ƃ��A�˂̐L��
��^�����Ƃ��A�˂̐L��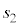 �́A�}8�̂悤��
�́A�}8�̂悤��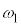 ��2�{�̊p�U�����Ŏ����I�ɑ������J��Ԃ����B���̂Ƃ��A
��2�{�̊p�U�����Ŏ����I�ɑ������J��Ԃ����B���̂Ƃ��A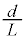 �̒l�����߂�B���o�ߒ��������B
�̒l�����߂�B���o�ߒ��������B
[��]
[2]�@���̕��͂�ǂ�ŁA�@�@�ɓK�������܂��͐��l���A{�@�@}����͓K�Ȃ��̂���I�т��̔ԍ����A���ꂼ��̉��ɋL������B�Ȃ��A�@�@�͂��ł��@�@�ŗ^����ꂽ���̂Ɠ������̂�\���B�܂��A��1�`��3�ł́A�w���ɂ��������āA�����ꂼ��̉��ɋL������B�������A�~������π�Ƃ���B
�^�̎��ԕω����Ȃ�������ł̉דd���q�̉^�����l���悤�B�דd���q�̉^���ɂ���Đ�����d��Ǝ���̉e���A����яd�͂̉e���͖������Ă悢�B
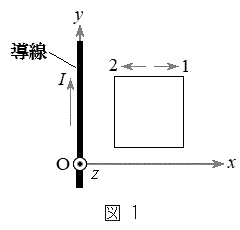 (1) �}1�̂悤�ɁAy����ɒu���ꂽ�\���ɒ���������̓����ɁAy���̐��̌����ɋ���I�̒��d��������Ă���ꍇ���l����B�^��̓�������μ�Ƃ���ƁA���̓d������鎥�����x�̑傫���́Ay�����狗��r���ꂽ�_���@�C�@�ƂȂ�Bxy���ʏ��
(1) �}1�̂悤�ɁAy����ɒu���ꂽ�\���ɒ���������̓����ɁAy���̐��̌����ɋ���I�̒��d��������Ă���ꍇ���l����B�^��̓�������μ�Ƃ���ƁA���̓d������鎥�����x�̑傫���́Ay�����狗��r���ꂽ�_���@�C�@�ƂȂ�Bxy���ʏ�� �C
�C �̗̈�ɁA�����`��1�����R�C����u���B�}1�Ɏ����悤�ɁA�e�ӂ�x�����邢��y���ɕ��s�ł���B�������A�R�C���̎��ȃC���_�N�^���X�͖����ł�����̂Ƃ���B�R�C����y���̐��̌����Ɉ��̑����œ����Ƃ��A�U���d����{���F�@�}��1�̌����ɗ����@�A�}��2�̌����ɗ����@�B����Ȃ�}�B�܂��A�R�C����x���̐��̌����Ɉ��̑����œ����Ƃ��A�U���d����{�n�F�@�}��1�̌����ɗ����@�A�}��2�̌����ɗ����@�B����Ȃ�}�B
�̗̈�ɁA�����`��1�����R�C����u���B�}1�Ɏ����悤�ɁA�e�ӂ�x�����邢��y���ɕ��s�ł���B�������A�R�C���̎��ȃC���_�N�^���X�͖����ł�����̂Ƃ���B�R�C����y���̐��̌����Ɉ��̑����œ����Ƃ��A�U���d����{���F�@�}��1�̌����ɗ����@�A�}��2�̌����ɗ����@�B����Ȃ�}�B�܂��A�R�C����x���̐��̌����Ɉ��̑����œ����Ƃ��A�U���d����{�n�F�@�}��1�̌����ɗ����@�A�}��2�̌����ɗ����@�B����Ȃ�}�B
 (2) ���ɁA���l�Ȏ��ꒆ�ł̉דd���q�̉^�����l���悤�B�דd���q�̑傫���͖����ł��A���̎��ʂ�m�C�d�ׂ�q(
(2) ���ɁA���l�Ȏ��ꒆ�ł̉דd���q�̉^�����l���悤�B�דd���q�̑傫���͖����ł��A���̎��ʂ�m�C�d�ׂ�q(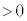 )�Ƃ���B�ȒP�̂��߁A�}2�Ɏ����悤�ȃ��f���ōl����B�����z���̕��̌����ɂ������Ă���A���̎������x�̑傫���́A����
)�Ƃ���B�ȒP�̂��߁A�}2�Ɏ����悤�ȃ��f���ōl����B�����z���̕��̌����ɂ������Ă���A���̎������x�̑傫���́A����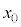 (
(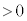 )�ɑ��āA
)�ɑ��āA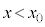 ��
��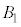 �C
�C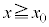 ��
��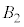 �Ƃ���B������
�Ƃ���B������ ��
��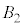 �͐��̒萔�ŁA
�͐��̒萔�ŁA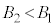 �ł���B�܂��A���q��
�ł���B�܂��A���q��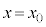 �Œ�߂��镽�ʂ�ʉ߂���Ƃ��A���̋O���͊��炩�ɂȂ���A�����͕ω����Ȃ����̂Ƃ���B
�Œ�߂��镽�ʂ�ʉ߂���Ƃ��A���̋O���͊��炩�ɂȂ���A�����͕ω����Ȃ����̂Ƃ���B����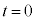 ��
��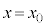 �C
�C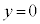 �C
�C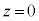 �ɂ���דd���q���Ax���̐��̌����ɑ���
�ɂ���דd���q���Ax���̐��̌����ɑ���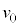 �ʼn^�����͂��߂��B�דd���q�͂܂��A
�ʼn^�����͂��߂��B�דd���q�͂܂��A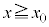 �̗̈�ɂ����ă��[�����c�͂ɂ��xy���ʓ��œ����~�^������B
�̗̈�ɂ����ă��[�����c�͂ɂ��xy���ʓ��œ����~�^������B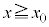 �ł̉~�O���̔��a���@�j�@�ƂȂ�B�דd���q��
�ł̉~�O���̔��a���@�j�@�ƂȂ�B�דd���q��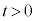 �ł͂��߂�
�ł͂��߂�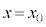 �ɓ��B����܂łɂ����鎞��
�ɓ��B����܂łɂ����鎞��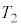 �́Am�C
�́Am�C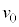 �Cq�C
�Cq�C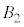 �C
�C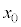 �̂����K�v�Ȃ��̂�p�����@�z�@�Ə�����B���̌�A���q��
�̂����K�v�Ȃ��̂�p�����@�z�@�Ə�����B���̌�A���q��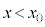 �ɂ����Ă������~�^������B
�ɂ����Ă������~�^������B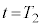 ����ӂ�����
����ӂ�����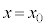 �ɓ��B����܂ł̎��Ԃ�
�ɓ��B����܂ł̎��Ԃ�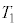 �Ƃ��A
�Ƃ��A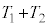 ���^���̎����Ƃ���B
���^���̎����Ƃ���B
��1�@����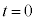 ���玞��
���玞��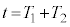 �܂ł̉דd���q��xy���ʓ��ł̋O����`���A����
�܂ł̉דd���q��xy���ʓ��ł̋O����`���A����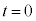 �C
�C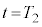 �C
�C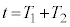 �ɂ�����ʒu�������B�܂��A����
�ɂ�����ʒu�������B�܂��A����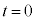 �ł̈ʒu���n�_�Ƃ��A
�ł̈ʒu���n�_�Ƃ��A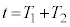 �ł̈ʒu���I�_�Ƃ���x�N�g���ɂ��āA���̑傫������B���̃x�N�g���ŕ\�����ړ����h���t�g�Ƃ�ԁB
�ł̈ʒu���I�_�Ƃ���x�N�g���ɂ��āA���̑傫������B���̃x�N�g���ŕ\�����ړ����h���t�g�Ƃ�ԁB
��1�ōl�@�����h���t�g�ɂ��āA���̕��ς̑��������߂悤�B�������x�̑傫���𐳂̒萔a�����d(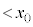 )��p����
)��p����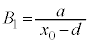 �C
�C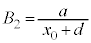 �Ɨ^����B�^���̎���
�Ɨ^����B�^���̎���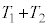 ��m�C
��m�C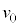 �Cq�Ca�Cd�C
�Cq�Ca�Cd�C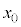 �̂����K�v�Ȃ��̂�p���ď������@�w�@�ƂȂ�B�h���t�g�̕��ς̑����́A�h���t�g��\���x�N�g���̑傫���������Ŋ��邱�Ƃɂ���ċ��߂��Am�C
�̂����K�v�Ȃ��̂�p���ď������@�w�@�ƂȂ�B�h���t�g�̕��ς̑����́A�h���t�g��\���x�N�g���̑傫���������Ŋ��邱�Ƃɂ���ċ��߂��Am�C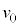 �Cq�Ca�Cd�C
�Cq�Ca�Cd�C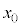 �̂����K�v�Ȃ��̂�p�����@�g�@�Ə�����B��ʂɁA��l�łȂ����ꂪ����ꍇ�ɂ��̂悤�ȃh���t�g�������A����͎�����z�h���t�g�Ƃ���B
�̂����K�v�Ȃ��̂�p�����@�g�@�Ə�����B��ʂɁA��l�łȂ����ꂪ����ꍇ�ɂ��̂悤�ȃh���t�g�������A����͎�����z�h���t�g�Ƃ���B 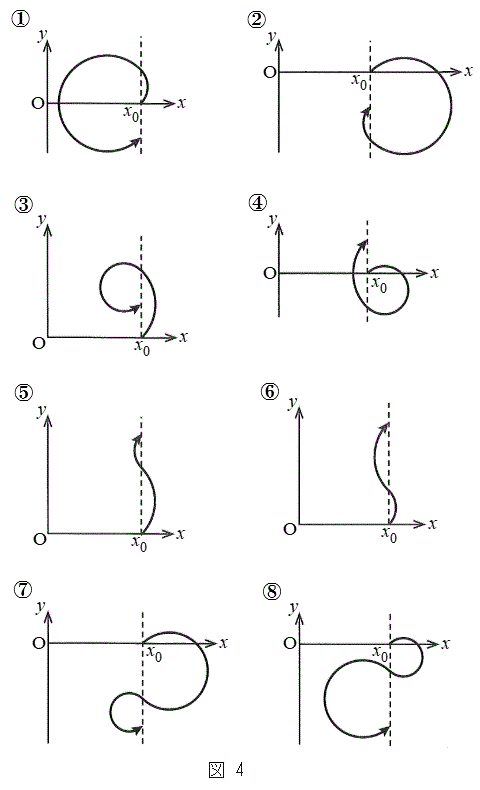 ��2�@
��2�@ ����A
����A ��2��ڂ�
��2��ڂ� �ɒB����Ƃ��܂ł̗��q�̋O���Ƃ��čł��K���Ȃ��̂�}4�̇@�`�G�̂�������I�сA�ԍ�����B
�ɒB����Ƃ��܂ł̗��q�̋O���Ƃ��čł��K���Ȃ��̂�}4�̇@�`�G�̂�������I�сA�ԍ�����B
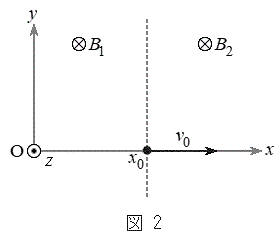
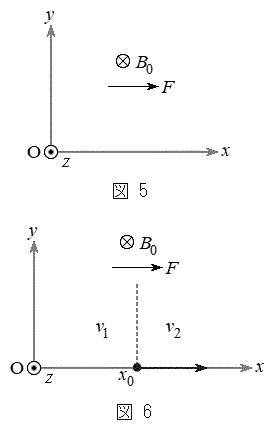 (3) ���ɁA��l�Ȏ���̂��Ƃ��A���[�����c�͂ɉ����ĊO�͂��דd���q�ɂ͂��炭�ꍇ���l���悤�B�דd���q�͎���m�C�d��q(
(3) ���ɁA��l�Ȏ���̂��Ƃ��A���[�����c�͂ɉ����ĊO�͂��דd���q�ɂ͂��炭�ꍇ���l���悤�B�דd���q�͎���m�C�d��q(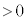 )�������A�傫���͖����ł���Ƃ���B�}5�̂悤�ɁAz���̕��̌����̈�l�Ȏ��ꂪ����A�������x�̑傫���𐳂̒萔
)�������A�傫���͖����ł���Ƃ���B�}5�̂悤�ɁAz���̕��̌����̈�l�Ȏ��ꂪ����A�������x�̑傫���𐳂̒萔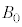 �Ƃ���B����ɁA���q�ɂ�x���̐��̌����ɑ傫��F�̈�l�ȕۑ��͂ł���O�͂���p����B���ꂨ��ъO�͂͂���������ԕϓ����Ȃ��B
�Ƃ���B����ɁA���q�ɂ�x���̐��̌����ɑ傫��F�̈�l�ȕۑ��͂ł���O�͂���p����B���ꂨ��ъO�͂͂���������ԕϓ����Ȃ��B���̂Ƃ��A�דd���q��x�������ɂ͈��͈̔͂Ŏ����I�ɐU������B�^�����̂��鎞���ŗ��q���Ax���ŏ��l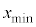 �ƂȂ�ʒu�ɂ��葬��
�ƂȂ�ʒu�ɂ��葬��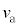 �������Ă����Ƃ���ƁAx���ő�l
�������Ă����Ƃ���ƁAx���ő�l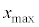 �ƂȂ�ʒu�܂ňړ������Ƃ��̑���
�ƂȂ�ʒu�܂ňړ������Ƃ��̑���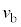 �́A���̊ԂɊO�͂������d��
�́A���̊ԂɊO�͂������d��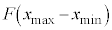 �����ł��邽��
�����ł��邽��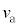 ���傫���Ȃ�B���̌�
���傫���Ȃ�B���̌�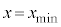 �ɂ��ǂ����Ƃ��A���q�̑�����
�ɂ��ǂ����Ƃ��A���q�̑�����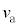 �ɔ�ׂ�{�`�F�@�傫���Ȃ�@�A�������Ȃ�@�B�ω����Ȃ�}�B
�ɔ�ׂ�{�`�F�@�傫���Ȃ�@�A�������Ȃ�@�B�ω����Ȃ�}�B
���[�����c�͂ɑ��ĊO�͂��\���Ɏア�Ƃ��A�דd���q�̉^���̓����~�^������̂���͂킸���ł���B�ȉ��ł́A�}6�̂悤�ɁA(2)�Ɠ��l��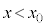 �̗̈��
�̗̈��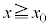 �̗̈�ɕ����A���̗��q�̉^�����Axy���ʓ��̂��ꂼ��̗̈�ŁA�قȂ鑬���œ����~�^�����郂�f���ōl�@�����B
�̗̈�ɕ����A���̗��q�̉^�����Axy���ʓ��̂��ꂼ��̗̈�ŁA�قȂ鑬���œ����~�^�����郂�f���ōl�@�����B
�דd���q�͎���ɂ�郍�[�����c�͂������A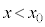 �ő���
�ő���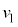 �C
�C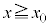 �ő���
�ő���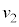 �̓����~�^�����s���Ƃ���B�����ŁA
�̓����~�^�����s���Ƃ���B�����ŁA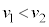 �ł���B�O�͂ɂ��
�ł���B�O�͂ɂ��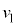 ��
��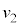 �̍��������A����ȊO�ɂ͊O�͂ɂ��^���ւ̉e���͂Ȃ��Ɖ��肷���B�܂��A
�̍��������A����ȊO�ɂ͊O�͂ɂ��^���ւ̉e���͂Ȃ��Ɖ��肷���B�܂��A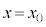 �ŗ��q�̋O���͊��炩�ɂȂ���Ƃ���B�������A��
�ŗ��q�̋O���͊��炩�ɂȂ���Ƃ���B�������A��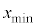 �����
�����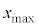 �͗p���Ȃ����ƁB
�͗p���Ȃ����ƁB
����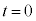 ��
��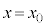 �C
�C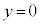 �C
�C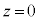 �ɂ���דd���q��x���̐��̌����ɑ���
�ɂ���דd���q��x���̐��̌����ɑ���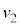 �œ����~�^�����͂��߂��B
�œ����~�^�����͂��߂��B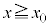 �ɂ����铙���~�^���̉~�̔��a���@���@�ƂȂ�A����
�ɂ����铙���~�^���̉~�̔��a���@���@�ƂȂ�A����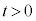 ��2��ڂ�
��2��ڂ�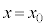 �ɒB����܂ł̎���T���@�k�@�ƂȂ�B����
�ɒB����܂ł̎���T���@�k�@�ƂȂ�B����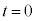 �ł̗��q�̈ʒu���n�_�A
�ł̗��q�̈ʒu���n�_�A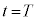 �ł̈ʒu���I�_�Ƃ���x�N�g�������̏ꍇ�̃h���t�g��\���B���̃x�N�g���̌�������Az���̕��̌����̎��ꂨ���x���̐��̌����̊O�͂ɂ����{���F�@x���̐��@�Ay���̐��@�Bx���̕��@�Cy���̕�}�̌����Ƀh���t�g���邱�Ƃ��킩��B���̃h���t�g�̕��ς̑����́A���̃x�N�g���̑傫��������T�Ŋ���AT��p�������@���@�Ƌ��߂���B���̃��f���ł́A
�ł̈ʒu���I�_�Ƃ���x�N�g�������̏ꍇ�̃h���t�g��\���B���̃x�N�g���̌�������Az���̕��̌����̎��ꂨ���x���̐��̌����̊O�͂ɂ����{���F�@x���̐��@�Ay���̐��@�Bx���̕��@�Cy���̕�}�̌����Ƀh���t�g���邱�Ƃ��킩��B���̃h���t�g�̕��ς̑����́A���̃x�N�g���̑傫��������T�Ŋ���AT��p�������@���@�Ƌ��߂���B���̃��f���ł́A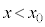 ��
��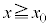 �̊e�̈�ɂ�����~�^���̔��a�����ꂼ��
�̊e�̈�ɂ�����~�^���̔��a�����ꂼ��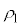 �C
�C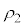 �Ƃ���ƁA���q��x��������
�Ƃ���ƁA���q��x��������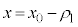 ��
��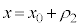 �̊Ԃ��ړ�����B
�̊Ԃ��ړ�����B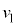 ��
��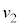 �̈Ⴂ�ɂ��^���G�l���M�[�̍���
�̈Ⴂ�ɂ��^���G�l���M�[�̍���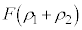 �ɓ������Ƃ���ƁA�@���@�́Am�Cq�CF�C
�ɓ������Ƃ���ƁA�@���@�́Am�Cq�CF�C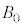 �C
�C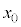 �̂����K�v�Ȃ��̂�p�����@���@�ƕ\�����Ƃ��ł���B
�̂����K�v�Ȃ��̂�p�����@���@�ƕ\�����Ƃ��ł���B
��3�@��l�ȊO�͂�����E�̓d��ɂ��͂̏ꍇ�A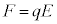 �Ƃ��āA�@���@�̃h���t�g�̕��ς̑��������߂�B�܂��A����
�Ƃ��āA�@���@�̃h���t�g�̕��ς̑��������߂�B�܂��A����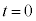 ����
����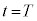 �܂ł̉דd���q��xy���ʓ��ł̋O����`���B����ɁA�����O���t�ɓd�ׂ�
�܂ł̉דd���q��xy���ʓ��ł̋O����`���B����ɁA�����O���t�ɓd�ׂ�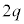 �̏ꍇ�̋O����2�������`���B�������A�ǂ����
�̏ꍇ�̋O����2�������`���B�������A�ǂ���� �ɂ����ď�̏����ʼn^�����͂��߂���̂Ƃ���B���ꂼ��̋O���ɓd�ׂ̒l�L���A�n�_�ƏI�_�̈Ⴂ���킩��悤�ɕ`�����ƁB
�ɂ����ď�̏����ʼn^�����͂��߂���̂Ƃ���B���ꂼ��̋O���ɓd�ׂ̒l�L���A�n�_�ƏI�_�̈Ⴂ���킩��悤�ɕ`�����ƁB �����ł͊ȒP�ȃ��f���ɂ���čl�@�������A���m�ȃh���t�g�̑������@���@�̒萔�{�ł���A���̂悤�ȊȒP�ȃ��f���ł��A�h���t�g�̓����邱�Ƃ��ł���B [��]
[3]�@���̕��͂�ǂ�ŁA�@�@�ɓK�������܂��͐��l���A{�@�@}����͓K�Ȃ��̂���I�т��̔ԍ����A���ꂼ��̉��ɋL������B�Ȃ��A�@�@�͂��ł��@�@�ŗ^����ꂽ���̂Ɠ������̂�\���B�܂��A��1�ł́A�w���ɂ��������āA�����ɋL������B�������A�~������π�Ƃ���B
�������������i�ނƂ��̂ӂ�܂����l���A��������p�������t�@�C�o�[�Ȃǂɂ��čl�@���悤�B�ȉ��ł͋�C�̋��ܗ���1�Ƃ���B
 (1) �}1�̂悤�ɋ��ܗ���
(1) �}1�̂悤�ɋ��ܗ��� �̕���A�Ƌ��ܗ���
�̕���A�Ƌ��ܗ���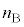 �̕���B������ȖʂŐڂ��Ă���A
�̕���B������ȖʂŐڂ��Ă���A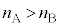 �Ƃ���BA����B�������˂����Ƃ��A���E�ʂ̖@���ɑ���p�x�Ƃ��āA���ˊp
�Ƃ���BA����B�������˂����Ƃ��A���E�ʂ̖@���ɑ���p�x�Ƃ��āA���ˊp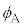 �C���ˊp
�C���ˊp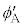 �C���܊p
�C���܊p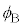 ���߂�B
���߂�B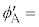 �@���@�ł���A
�@���@�ł���A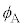 �C
�C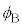 �C
�C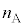 �C
�C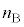 �̊W��
�̊W��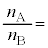 �@���@�ƂȂ�B
�@���@�ƂȂ�B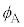 ������l
������l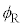 ���傫���Ƃ��A���͋��E�ʂőS���˂����B
���傫���Ƃ��A���͋��E�ʂőS���˂����B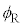 ��
��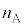 �C
�C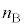 �̊W��
�̊W��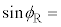 �@���@�ł���B
�@���@�ł���B
 (2) ���t�@�C�o�[�́A�}2(a)�̂悤�ɋ��ܗ��̈قȂ�K���X����̍א��ɂ������̂ł���B���S�������R�A�A�O���������N���b�h�Ƃ�ԁB�R�A�ƃN���b�h�̋��ܗ������ꂼ��
(2) ���t�@�C�o�[�́A�}2(a)�̂悤�ɋ��ܗ��̈قȂ�K���X����̍א��ɂ������̂ł���B���S�������R�A�A�O���������N���b�h�Ƃ�ԁB�R�A�ƃN���b�h�̋��ܗ������ꂼ��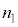 (
( )�C
)�C (
(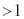 )�Ƃ���B�܂��A�R�A�̎����܂ޕ��ʓ���i�ތ����l����B
)�Ƃ���B�܂��A�R�A�̎����܂ޕ��ʓ���i�ތ����l����B���ܗ��̊W��{���F�@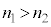 �C�A
�C�A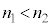 �C�B
�C�B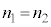 }�ŁA����ɃR�A���Ō��̐i�ޕ����ƌ��t�@�C�o�[�̎������̂Ȃ��p�xθ������p�x
}�ŁA����ɃR�A���Ō��̐i�ޕ����ƌ��t�@�C�o�[�̎������̂Ȃ��p�xθ������p�x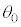 ��菬������A�}2(b)�̂悤�Ɍ��̓R�A�ƃN���b�h�̋��E�őS���˂����B(1)�ł̋c�_���ӂ܂���ƁA
��菬������A�}2(b)�̂悤�Ɍ��̓R�A�ƃN���b�h�̋��E�őS���˂����B(1)�ł̋c�_���ӂ܂���ƁA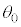 ��
��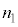 �����
�����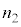 �̊W��
�̊W��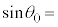 �@���@�ƂȂ�B���̂悤�Ɍ����R�A�ƃN���b�h�̋��E�ʂőS���˂���邽�߂ɂ́A���t�@�C�o�[�̒[�ʂɂ����ċ�C������R�A�Ɍ������˂���ۂɁA�������ɑ�����̓��ˊp
�@���@�ƂȂ�B���̂悤�Ɍ����R�A�ƃN���b�h�̋��E�ʂőS���˂���邽�߂ɂ́A���t�@�C�o�[�̒[�ʂɂ����ċ�C������R�A�Ɍ������˂���ۂɁA�������ɑ�����̓��ˊp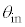 ��������������K�v������B���̏������A
��������������K�v������B���̏������A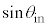 �C
�C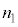 �C
�C ��p���ĕ\���ƁA�@���@
��p���ĕ\���ƁA�@���@ �ƂȂ�B�������A���t�@�C�o�[�̒[�ʂ͂��̎������ɑ��Đ����ł���Ƃ��A�[�ʂɂ����ăR�A�̎��ォ����˂�������l����B
�ƂȂ�B�������A���t�@�C�o�[�̒[�ʂ͂��̎������ɑ��Đ����ł���Ƃ��A�[�ʂɂ����ăR�A�̎��ォ����˂�������l����B
 (3) ���˂����������t�@�C�o�[����i�ނ��߂ɂ́A(2)�̏��������ł͕s�\���ł���B������l�@���悤�B
(3) ���˂����������t�@�C�o�[����i�ނ��߂ɂ́A(2)�̏��������ł͕s�\���ł���B������l�@���悤�B�R�A�̎����܂ޕ��ʓ���i�ތ����l����B�}3�̂悤�ɁA�R�A���̌��̔g����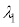 �Ƃ��A���̐i�s�����ƃR�A�̎������̂Ȃ��p�x��θ�Ƃ���B���̂Ƃ��A�a�����̔g�ʊԂ̋�����
�Ƃ��A���̐i�s�����ƃR�A�̎������̂Ȃ��p�x��θ�Ƃ���B���̂Ƃ��A�a�����̔g�ʊԂ̋�����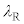 �Ƃ���ƁA
�Ƃ���ƁA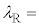 �@���@�ƂȂ��Ă���B���������āA�a�����ɂ͔g����
�@���@�ƂȂ��Ă���B���������āA�a�����ɂ͔g����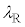 �̔g�������Ă���Ƃ݂Ȃ���B
�̔g�������Ă���Ƃ݂Ȃ���B
���a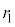 �̃R�A���Ō�����܂炸�ɐi��ł����Ƃ��A�a�����ɂ͒�ݔg���`������Ă���B�����ł́A�c�_���ȒP�ɂ��邽�߁A���R��N�ɑ��A�R�A�̒��a��
�̃R�A���Ō�����܂炸�ɐi��ł����Ƃ��A�a�����ɂ͒�ݔg���`������Ă���B�����ł́A�c�_���ȒP�ɂ��邽�߁A���R��N�ɑ��A�R�A�̒��a��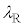 ��
��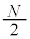 �{�ł�����̂悤�Ȓ�ݔg���`�������Ƃ���B���̂Ƃ��A
�{�ł�����̂悤�Ȓ�ݔg���`�������Ƃ���B���̂Ƃ��A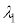 �C
�C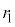 �CN��p���āA
�CN��p���āA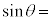 �@���@�ƕ\����B
�@���@�ƕ\����B
���ۂɌ��t�@�C�o�[���g���ۂɂ́A��C���ł̔g����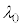 �̌��������Y���ŏW�����ăR�A�ɓ��˂����邽�߁A���͂��܂��܂�
�̌��������Y���ŏW�����ăR�A�ɓ��˂����邽�߁A���͂��܂��܂�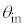 �œ��˂��A���˒����θ�͘A���I�Ȓl����������B���̂���
�œ��˂��A���˒����θ�͘A���I�Ȓl����������B���̂���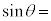 �@���@�����ƂтƂт̒l��θ�������������R�A����i�ނ��Ƃ��ł���BN�œ����Â����邱�̌������[�h�Ƃ�ԁB����A����N�̃��[�h�ɂ��āA
�@���@�����ƂтƂт̒l��θ�������������R�A����i�ނ��Ƃ��ł���BN�œ����Â����邱�̌������[�h�Ƃ�ԁB����A����N�̃��[�h�ɂ��āA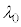 ������l
������l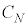 ���傫���Ƃ��A���̃��[�h�̓R�A�ƃN���b�h�̋��E�őS���˂ł����`���Ȃ��Ȃ�B
���傫���Ƃ��A���̃��[�h�̓R�A�ƃN���b�h�̋��E�őS���˂ł����`���Ȃ��Ȃ�B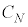 ��
��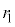 �C
�C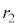 �CN�C
�CN�C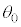 ��p���ĕ\���ƁA
��p���ĕ\���ƁA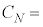 �@���@�ƂȂ�B�����ŁA
�@���@�ƂȂ�B�����ŁA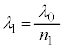 �̊W��p����B
�̊W��p����B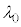 ��
��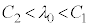 �����Ƃ��A�R�A����`������
�����Ƃ��A�R�A����`������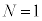 �̃��[�h�݂̂ƂȂ�B����
�̃��[�h�݂̂ƂȂ�B����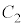 �̓J�b�g�I�t�g���Ƃ��A
�̓J�b�g�I�t�g���Ƃ��A �C
�C �C
�C ��p�����@���@�ƕ\����B
��p�����@���@�ƕ\����B
 (4) �ȉ��ł́A
(4) �ȉ��ł́A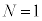 �̃��[�h�������`���ꍇ���l����B�R�A���̔g����
�̃��[�h�������`���ꍇ���l����B�R�A���̔g����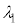 �̌��́A�}4�̂悤�Ȕg�̍����̌��ʁA�������Ɛ����Ȕg�ʂ����g�Ƃ݂Ȃ���B�܂��Aθ���������ꍇ���l���A�������ꂽ���̔g����
�̌��́A�}4�̂悤�Ȕg�̍����̌��ʁA�������Ɛ����Ȕg�ʂ����g�Ƃ݂Ȃ���B�܂��Aθ���������ꍇ���l���A�������ꂽ���̔g����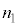 �ɓ������Ƃ���B
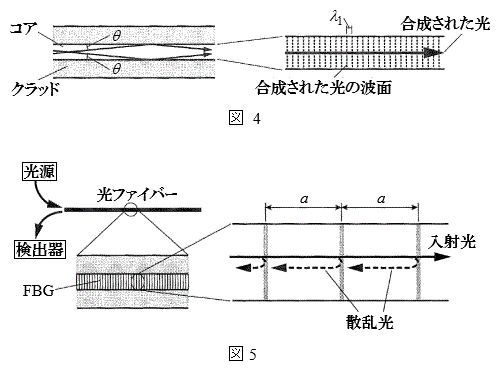
�ɓ������Ƃ���B�}5�̂悤�ɁA���t�@�C�o�[�̃R�A�ɁA�����U������\���������I�Ɏ������ɓ����������̂��l����B������t�@�C�o�[�E�u���b�O�E�O���[�e�B���O(FBG)�Ƃ����B���̍\���̎�����a�Ƃ���ƁAFBG�͊Ԋua�̉�܊i�q�̂悤�ɂ͂��炭�B���Ȃ킿�A���˂������̂����ꕔ���U������ē��ˑ��ւƕԂ��Ă������A��������a���ꂽ�ʒu����̎U���������ߍ����Ƃ����������Ԃ��Ă����A�}5�̌��o��Ō��o���邱�Ƃ��ł���B�������ɕԂ��Ă����������ߍ�����������A���o�ł�����̍ł������g���́Aa�C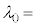 ��p����
��p���� �@���@�ƕ\�����Ƃ��ł���B���o�킪���o����̂͋�C���̔g���ł��邱�Ƃɒ��ӂ���B�ȉ��ł͋��ߍ����ĕԂ��Ă������̂����g�����@���@�̌����l���A����ˌ��ƌĂԁB
�@���@�ƕ\�����Ƃ��ł���B���o�킪���o����̂͋�C���̔g���ł��邱�Ƃɒ��ӂ���B�ȉ��ł͋��ߍ����ĕԂ��Ă������̂����g�����@���@�̌����l���A����ˌ��ƌĂԁB
 (5) FBG���܂ތ��t�@�C�o�[�̈ꕔ�����l����B���ꂪ����D�̏�Ԃ���D�Ƃ���ׂď\���ɏ�������
(5) FBG���܂ތ��t�@�C�o�[�̈ꕔ�����l����B���ꂪ����D�̏�Ԃ���D�Ƃ���ׂď\���ɏ������� ������l�ɐL�k���A������
������l�ɐL�k���A������ �ɂȂ�ƁAFBG�̎�����a����
�ɂȂ�ƁAFBG�̎�����a����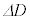 �ɕω�����B���̏ꍇ�AD�C
�ɕω�����B���̏ꍇ�AD�C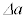 �Ca�C
�Ca�C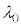 �̊W���@���@�ł���B�܂��A���̎����̕ω��ɂ��AFBG����̔��ˌ��̔g����
�̊W���@���@�ł���B�܂��A���̎����̕ω��ɂ��AFBG����̔��ˌ��̔g����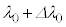 ����
����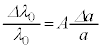 �ɕω�����B���̔g���͍����x�Ɍv���ł��邽�߁AFBG�͔����ȐL�k�����o����Z���T�[�Ƃ��ė��p�ł���B�����ŁAA��萔�Ƃ��āA
�ɕω�����B���̔g���͍����x�Ɍv���ł��邽�߁AFBG�͔����ȐL�k�����o����Z���T�[�Ƃ��ė��p�ł���B�����ŁAA��萔�Ƃ��āA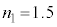 �Ƃ����BA�͐L�k�ɂƂ��Ȃ�FBG���̃R�A�̋��ܗ��̔����ȕω��̉e���Ȃǂ��܂W���ł���B
�Ƃ����BA�͐L�k�ɂƂ��Ȃ�FBG���̃R�A�̋��ܗ��̔����ȕω��̉e���Ȃǂ��܂W���ł���B
A�����肷�邽�߁A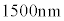 �̌��t�@�C�o�[�ɔg����
�̌��t�@�C�o�[�ɔg����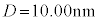 �t�߂̘A���X�y�N�g���̌������AFBG���܂ޕ����̒�����
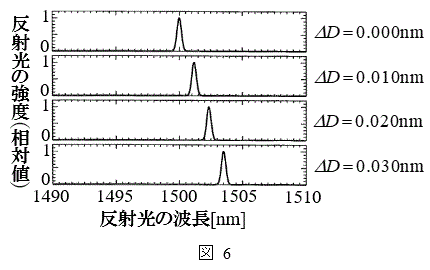
�t�߂̘A���X�y�N�g���̌������AFBG���܂ޕ����̒�����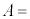 ����ω������Ȃ���AFBG����̔��ˌ��̋��x�Ɣg���̊W����C���ő��肵���B����ƁA�}6�̌��ʂ�����ꂽ�B���̌��ʂ���W��A�͗L������1����
����ω������Ȃ���AFBG����̔��ˌ��̋��x�Ɣg���̊W����C���ő��肵���B����ƁA�}6�̌��ʂ�����ꂽ�B���̌��ʂ���W��A�͗L������1����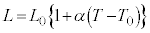 �@���@�Ƌ��߂邱�Ƃ��ł���B
�@���@�Ƌ��߂邱�Ƃ��ł���B
FBG�̉��p��̈�ɁA�M�c�����肪����B�ő̕����̒�����L�C��Ή��x��T�Ƃ���ƁA�����̕����͎����t�߂ɂ�����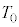 �Ƃ����W�������B�W��α�͐��c�����A
�Ƃ����W�������B�W��α�͐��c�����A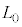 �͎����ɋ߂�����x�A
�͎����ɋ߂�����x�A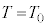 ��
��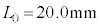 �ł̒����ł���B
�ł̒����ł���B
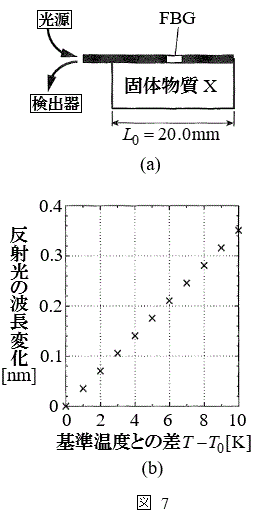 ��q��FBG���A����
��q��FBG���A����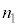 �̌ő̕���X�̎����ɐ}7(a)�̂悤�ɓ\��t�����BX�͈�l�ɔM�c�����A���t�@�C�o�[��X�̔M�c���Ɋ��S�ɒǐ����ĐL�k����Ɖ��肷��B�܂��A���x�ω��ɂ��
�̌ő̕���X�̎����ɐ}7(a)�̂悤�ɓ\��t�����BX�͈�l�ɔM�c�����A���t�@�C�o�[��X�̔M�c���Ɋ��S�ɒǐ����ĐL�k����Ɖ��肷��B�܂��A���x�ω��ɂ��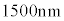 �̕ω��͔����ł���BFBG�ɋ�C���ł̔g����
�̕ω��͔����ł���BFBG�ɋ�C���ł̔g����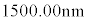 �t�߂̘A���X�y�N�g���̌�������ƁA����x�ɂ�����
�t�߂̘A���X�y�N�g���̌�������ƁA����x�ɂ�����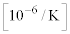 �̌������˂���A���x��ς��Ȃ��甽�ˌ��̋�C���ł̔g���̕ω��𑪒肵�����ʁA�}7(b)������ꂽ�B�������A�����̔M�c���ȊO�ɋN������g���̕ω��͍��������Ă���B�\1��X�̌�╨���Ƃ����̐��c�����ł���B
�̌������˂���A���x��ς��Ȃ��甽�ˌ��̋�C���ł̔g���̕ω��𑪒肵�����ʁA�}7(b)������ꂽ�B�������A�����̔M�c���ȊO�ɋN������g���̕ω��͍��������Ă���B�\1��X�̌�╨���Ƃ����̐��c�����ł���B
��1�@�������ʂ�A�̒l��p���AX���\1�̂ǂ̕������𐄒肹��B�c�_�̉ߒ��������B
�\1
| �@�������@ | ���c����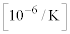 |
| ���� | 8.8 |
| �� | 18.9 |
| ���� | 30.2 |
[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B