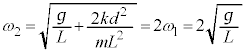���啨��'24�N�O��[1]
���̕��͂�ǂ�ŁA�@�@�ɓK�������܂��͐��l���A���ꂼ��̉��ɋL������B�Ȃ��A�@�@�͂��ł��@�@�ŗ^����ꂽ���̂Ɠ������̂�\���B�܂��A��1�C��2�ł́A�w���ɂ��������āA�����ꂼ��̉��ɋL������B�������A�~������π�C�d�͉����x��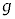 �Ƃ���B��C�̒�R�͖����ł�����̂Ƃ���B
�Ƃ���B��C�̒�R�͖����ł�����̂Ƃ���B
 (1) �}1�̂悤�ɁA���ʂ������ł���ł��_�̉��[�ɁA���ʂ�m�ŏ��������`�̂���������t�����U��q�ɂ��čl����B�_�͏�[�̌Œ�_R���x�_�Ƃ��āAR���܂މ����ʓ������炩�ɉ�]����B�Œ�_���炨����̏d�S(�_�̉��[)�܂ł̋�����L�C�~���ɉ������ʼn��_O����̂�����̕ψʂ�x(�E������)�A����������̖_�̉�]�p��θ(�����v���𐳁A�P�ʂ̓��W�A��)�Ƃ���B
(1) �}1�̂悤�ɁA���ʂ������ł���ł��_�̉��[�ɁA���ʂ�m�ŏ��������`�̂���������t�����U��q�ɂ��čl����B�_�͏�[�̌Œ�_R���x�_�Ƃ��āAR���܂މ����ʓ������炩�ɉ�]����B�Œ�_���炨����̏d�S(�_�̉��[)�܂ł̋�����L�C�~���ɉ������ʼn��_O����̂�����̕ψʂ�x(�E������)�A����������̖_�̉�]�p��θ(�����v���𐳁A�P�ʂ̓��W�A��)�Ƃ���B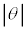 �͏\���ɏ������A�Ƃ��ɂ��Ƃ��̂Ȃ�����
�͏\���ɏ������A�Ƃ��ɂ��Ƃ��̂Ȃ�����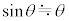 �C
�C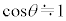 �Ƌߎ�����B
�Ƌߎ�����B������̉~�������̉����x��a(�E������)�Ƃ���Ƃ��A������̉~�������̉^����������a�Cm�CL�C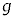 �Cx��p����
�Cx��p���� 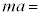 �@�A�@
�@�A�@ ��1�@�}3�̈ʒu���炨����B�݂̂��E�����Ɏ����グ�ĐÂ��ɗ����A����
��1�@�}3�̈ʒu���炨����B�݂̂��E�����Ɏ����グ�ĐÂ��ɗ����A���� �ɂ����č������ɑ���
�ɂ����č������ɑ��� �ł�����A�ɏՓ˂������B
�ł�����A�ɏՓ˂������B �̊W�����藧�Ƃ��A�}4�����ɕ`���ʂ��āA2�̂����肪
�̊W�����藧�Ƃ��A�}4�����ɕ`���ʂ��āA2�̂����肪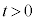 ��3��Փ˂���܂ł̂�����A�CB�̉~�������̕ψ�
��3��Փ˂���܂ł̂�����A�CB�̉~�������̕ψ� �C
�C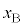 �Ǝ���t�̊W���A���ꂼ���������ѓ_���ŕ`���B�O���t�ɂ́A���ꂼ��̂�����̕ψʂ̐U���Ƃ����肪�Փ˂��鎞�����Ak��p�����Ɏ����B�����̓��o�ߒ����L�q����B
�Ǝ���t�̊W���A���ꂼ���������ѓ_���ŕ`���B�O���t�ɂ́A���ꂼ��̂�����̕ψʂ̐U���Ƃ����肪�Փ˂��鎞�����Ak��p�����Ɏ����B�����̓��o�ߒ����L�q����B
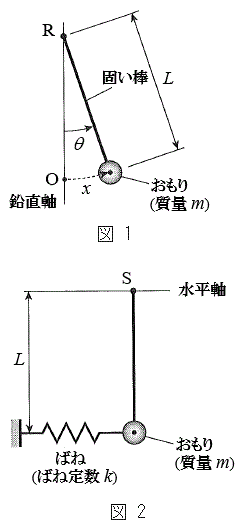
 �}2�̐U��q�ɂ����āA�}5�̂悤�ɁA�˂̈ʒu���Œ�_S���狗��d�̈ʒu�ɕύX�����B������̉~�������̕ψʂ�x�̂Ƃ��A�˂̐L�т��@�J�@�ł���B
�}2�̐U��q�ɂ����āA�}5�̂悤�ɁA�˂̈ʒu���Œ�_S���狗��d�̈ʒu�ɕύX�����B������̉~�������̕ψʂ�x�̂Ƃ��A�˂̐L�т��@�J�@�ł���B
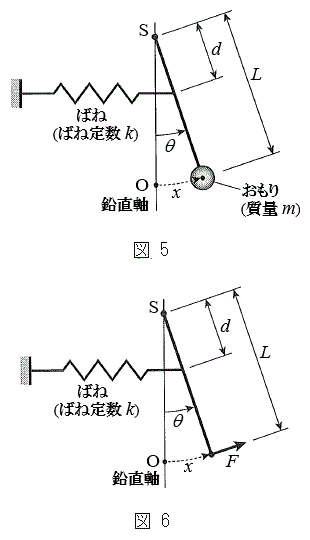
�����ŁA������ɂ͂��炭�͂𗝉����邽�߁A�U��q�̉^�����ɂ�����Ɩ_�̊Ԃɂ͂��炭�͂��l����B�}6�̂悤�ɁA�����肩��_�̉��[�ɍ�p����͂̉~������������F(�E������)�Ƃ���B�˂Ɩ_�̎��ʂ͖����ł��邽�߁A�_�ɂ͂��炭�͂̓_S�܂��̃��[�����g�̂肠�����A�Î~���Ă���Ƃ��Ɠ��l�ɐ��藧�B���������āAF��L�Cd�Ck�Cx��p����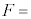 �@�L�@�ƕ\����B�}5�̂˕t���U��q�ɂ����āA�_���炨����ɂ͐}6��F�̔���p���͂��炫�A������̉~�������̉^���������͎��̂悤�ɕ\�����Ƃ��ł���B
�@�L�@�ƕ\����B�}5�̂˕t���U��q�ɂ����āA�_���炨����ɂ͐}6��F�̔���p���͂��炫�A������̉~�������̉^���������͎��̂悤�ɕ\�����Ƃ��ł���B �@�A�@�|F
�@�A�@�|F���̂˕t���U��q�͒P�U�����A���̊p�U�������@�N�@�ł���B
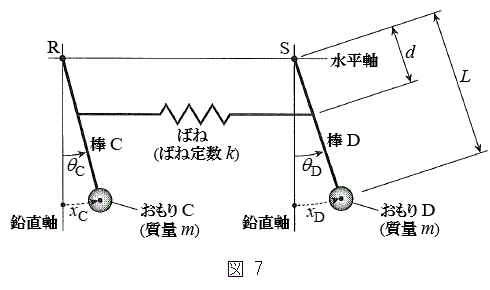 (2) �}7�̂悤�ɁA�}1�̐U��q2�����ꂼ��Œ�_R�CS�Ŏx�����A���ʂ������ł���˂��A�Œ�_���狗��d�̈ʒu�Ɏ��t�����B�˂͏\���ɒ����A�˂��X�����Ƃɂ��A�˂̐L�сA����ѕ����͂̑傫���ƕ����ւ̉e���͖����ł���B�˒萔��k�Ƃ��A�˂́A�_C�CD�̉�]�p
(2) �}7�̂悤�ɁA�}1�̐U��q2�����ꂼ��Œ�_R�CS�Ŏx�����A���ʂ������ł���˂��A�Œ�_���狗��d�̈ʒu�Ɏ��t�����B�˂͏\���ɒ����A�˂��X�����Ƃɂ��A�˂̐L�сA����ѕ����͂̑傫���ƕ����ւ̉e���͖����ł���B�˒萔��k�Ƃ��A�˂́A�_C�CD�̉�]�p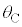 �C
�C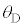 ���Ƃ���0�̂Ƃ����R���ł���B
���Ƃ���0�̂Ƃ����R���ł���B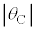 �C
�C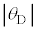 �͏\���ɏ������A
�͏\���ɏ������A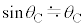 �C
�C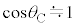 �C
�C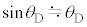 �C
�C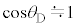 �Ƌߎ�����B
�Ƌߎ�����B������C�CD�̍ʼn��_����̉~���ɉ������ψʂ�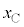 �C
�C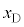 (�E������)�Ƃ���ƁA�˂̐L��
(�E������)�Ƃ���ƁA�˂̐L��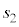 ���@�P�@�ƕ\����B������C�CD�̉~�������̉����x��
���@�P�@�ƕ\����B������C�CD�̉~�������̉����x��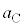 �C
�C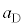 (�E������)�Ƃ���ƁA������C�CD�̉~�������̉^���������́A
(�E������)�Ƃ���ƁA������C�CD�̉~�������̉^���������́A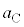 �C
�C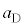 �Cm�CL�C
�Cm�CL�C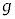 �Cd�Ck�C
�Cd�Ck�C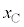 �C
�C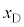 ��p���Ď����ŕ\�����B
��p���Ď����ŕ\�����B 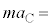 �@�R�@
�@�R�@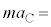 �@�T�@
�@�T�@2�̐U��q�������p�U����ω�ŒP�U��������ʂȏ�Ԃ��l����Ƃ��A���������藧�B
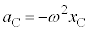 �C
�C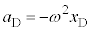
�㎮���^���������ɑ�����A
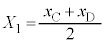 �C
�C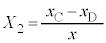
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@[�N]�܂ł͕��}�ł����A�I�Ղ����ł��B[�R][�T]�́A[�J][�L]���˂̉e�����ǂ��������Ƃ����q���g�ɂȂ��Ă���o��Ӑ}�������������ōl����K�v������܂��B��2�͌���ꂽ�������Ԃ̒��ŏo��Ӑ}��c������͖̂����ȋC�����܂��B
(1) ������ɂ͂��炭�d�͂̉~�����������͉E�������Ȃ̂ŁA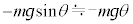 �ł��B
�ł��B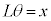 ���A
���A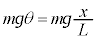 �C����āA������̉~�������̉����x��a�Ƃ��āA������̉~���������^���������́A
�C����āA������̉~�������̉����x��a�Ƃ��āA������̉~���������^���������́A
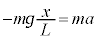 �@
�@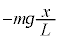 ......[�A]
......[�A]����āA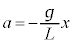 �C�P�U���̌����F
�C�P�U���̌����F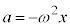 ���A�p�U����ω�́A
���A�p�U����ω�́A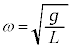 ......[�C]
......[�C]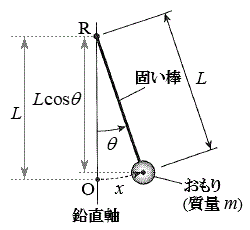 �E�}���A�ψʂ�
�E�}���A�ψʂ�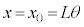 �̂Ƃ��A�������
�̂Ƃ��A�������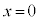 �̂Ƃ�����
�̂Ƃ�����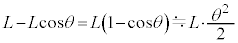 ���������ʒu�ɂ���A��������ʒu�G�l���M�[�́A
���������ʒu�ɂ���A��������ʒu�G�l���M�[�́A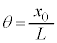 ���A
���A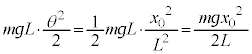 �C������̑��x��
�C������̑��x��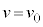 �Ȃ̂ŁA������̗͊w�I�G�l���M�[�́A
�Ȃ̂ŁA������̗͊w�I�G�l���M�[�́A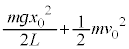 ......[�E]
......[�E]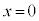 �ɂȂ����Ƃ��A������̈ʒu�G�l���M�[��0�ŁA���̂Ƃ��̂�����̉~�������̑�����
�ɂȂ����Ƃ��A������̈ʒu�G�l���M�[��0�ŁA���̂Ƃ��̂�����̉~�������̑�����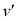 �Ƃ��āA�͊w�I�G�l���M�[�ۑ����A
�Ƃ��āA�͊w�I�G�l���M�[�ۑ����A
������A�ɓ����͂́A�˂̒e����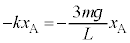 �ƁA������A�ɓ����d�͂̉~������������[�A]�Ɠ��l�ɂ���
�ƁA������A�ɓ����d�͂̉~������������[�A]�Ɠ��l�ɂ���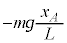 �ł��B������A�̉^���������͉����x��
�ł��B������A�̉^���������͉����x��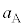 �Ƃ��āA
�Ƃ��āA 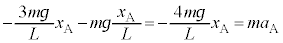 �@��
�@�� 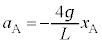
������A�̊p�U����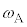 �́A
�́A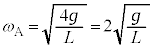 �C�U��
�C�U��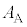 ��
��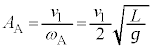 �C������A�͔�������A
�C������A�͔�������A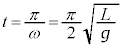 �ɍʼn��_
�ɍʼn��_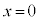 �ɖ߂��Ă��܂��B�����ŁA������A�͐Î~���Ă���������B�ƁA
�ɖ߂��Ă��܂��B�����ŁA������A�͐Î~���Ă���������B�ƁA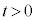 �ɂ�����1��ڂ̏Փ˂��s�����x���������A�Փ˒���A������A�͐Î~��(�˂̒e���͂�0)�A������B�͑���
�ɂ�����1��ڂ̏Փ˂��s�����x���������A�Փ˒���A������A�͐Î~��(�˂̒e���͂�0)�A������B�͑���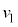 �ʼnE�����ɓ����܂��B
�ʼnE�����ɓ����܂��B
������B�ɓ����͂́A�d�͂̉~����������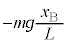 �ŁA������B�̉^���������͉����x��
�ŁA������B�̉^���������͉����x��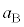 �Ƃ��āA
�Ƃ��āA 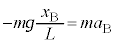 �@��
�@�� 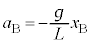
 ������B�̊p�U����
������B�̊p�U���� �́A
�́A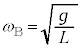 �C�U��
�C�U��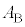 ��
��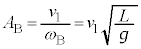 �C������B�͔�������A
�C������B�͔�������A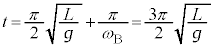 �ɍʼn��_
�ɍʼn��_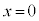 �ɖ߂��Ă��܂��B�����ŁA������B�͐Î~���Ă���������A��
�ɖ߂��Ă��܂��B�����ŁA������B�͐Î~���Ă���������A��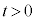 �ɂ�����2��ڂ̏Փ˂��s�����x���������A�Փ˒���A������A�͑���
�ɂ�����2��ڂ̏Փ˂��s�����x���������A�Փ˒���A������A�͑���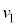 �ō������ɓ����A������B�͐Î~���܂��B������A�́A
�ō������ɓ����A������B�͐Î~���܂��B������A�́A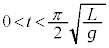 �ɂ�����P�U���Ɠ����P�U�������Ĕ�������A
�ɂ�����P�U���Ɠ����P�U�������Ĕ�������A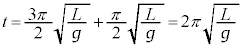 �ɍʼn��_
�ɍʼn��_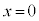 �ɖ߂�Î~���Ă��邨����B�ƁA
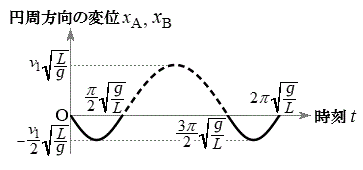
�ɖ߂�Î~���Ă��邨����B�ƁA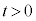 �ɂ�����3��ڂ̏Փ˂����܂��B����āA�����܂ł́A������A�C������B�̉~�������̕ψ�
�ɂ�����3��ڂ̏Փ˂����܂��B����āA�����܂ł́A������A�C������B�̉~�������̕ψ�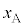 (�E�}����)�C
(�E�}����)�C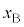 (�E�}�_��)�Ǝ���t�̊W�͉E�}�̂悤�ɂȂ�܂��B
(�E�}�_��)�Ǝ���t�̊W�͉E�}�̂悤�ɂȂ�܂��B�}5�ɂ����āA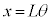 ���A�˂̐L�т́A
���A�˂̐L�т́A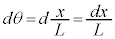 ......[�J]�˂��_�𐅕������������Ɉ����͂̑傫����
......[�J]�˂��_�𐅕������������Ɉ����͂̑傫����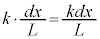 �C���̗͂�S�_�̂܂����͂̃��[�����g�́A���ł̒�����
�C���̗͂�S�_�̂܂����͂̃��[�����g�́A���ł̒�����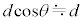 �ƂȂ�̂ŁA���v����
�ƂȂ�̂ŁA���v����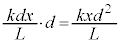 �C��F�̃��[�����g�́A���ł̒�����L�ŁA�����v����
�C��F�̃��[�����g�́A���ł̒�����L�ŁA�����v����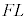 �CS�_�̂܂��̗͂̃��[�����g�̂荇�����A
�CS�_�̂܂��̗͂̃��[�����g�̂荇�����A 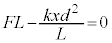 �@��
�@�� 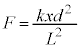 ......[�L]
......[�L]�����肪�_�ɋy�ڂ���F������p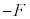 ���A�_��������ɋy�ڂ��͂ɂȂ邱�Ƃɒ��ӂ��āA������̉^���������́A�����x��a�Ƃ��āA[�A]�̌��ʂ�p���āA
���A�_��������ɋy�ڂ��͂ɂȂ邱�Ƃɒ��ӂ��āA������̉^���������́A�����x��a�Ƃ��āA[�A]�̌��ʂ�p���āA 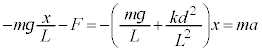 �@����@
�@����@�� 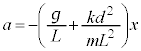 �p�U����ω�́A
�p�U����ω�́A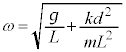 ......[�N]
......[�N]
(2) �}7�����Ă���ƁA[�J]�Ɠ��l�ɂ��āA�˂̍����ŁA�_D�̂˂Ƃ̐ڑ��_�́A�E��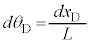 �ψʂ��A�_C�Ƃ˂Ƃ̐ڑ��_�́A�E��
�ψʂ��A�_C�Ƃ˂Ƃ̐ڑ��_�́A�E��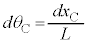 �ψʂ��Ă���̂ŁA�˂̐L��
�ψʂ��Ă���̂ŁA�˂̐L�� �́A
�́A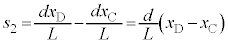 ......[�P]
......[�P] ����āA[�L]��F�́A�����ł͂˂̐L�т�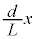 ��
��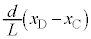 �Ƃ��āA
�Ƃ��āA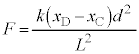 �ƍl���܂��B
�ƍl���܂��B
�@�Ɠ��l�ɍl����ƁA������D����͂́A�d�͂̉~����������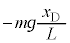 �ƁA�_D��������D�ɋy�ڂ���
�ƁA�_D��������D�ɋy�ڂ���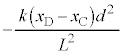 (��������)�ł��B������D�̉^���������́A�����x��
(��������)�ł��B������D�̉^���������́A�����x��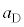 �Ƃ��āA
�Ƃ��āA 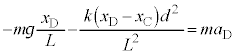 �@����A
�@����A�@�Ɠ��l�ɍl���āA�_C��������C�ɋy�ڂ��͂́A�˂��_C�ɋy�ڂ��͂Ɠ��������ɂȂ邱�Ƃɒ��ӂ��āA������C����͂́A�_C��������C�ɋy�ڂ���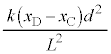 (��������)�ƁA�d�͂̉~����������
(��������)�ƁA�d�͂̉~����������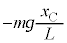 �ŁA������C�̉^���������́A�����x��
�ŁA������C�̉^���������́A�����x��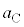 �Ƃ��āA
�Ƃ��āA 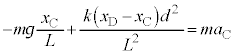 �@����B
�@����B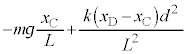 ......[�R]�C
......[�R]�C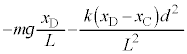 ......[�T]�A�{�B���(���Ή^�����Q��)�A
......[�T]�A�{�B���(���Ή^�����Q��)�A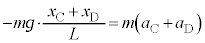 �@��
�@�� 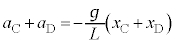
����āA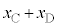 �͊p�U����
�͊p�U����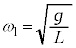 �̒P�U�������܂��B
�̒P�U�������܂��B
�A�|�B���A 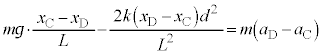 �@��
�@�� 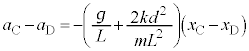
����āA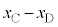 �͊p�U����
�͊p�U����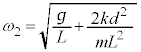 �̒P�U�������܂��B�@
�̒P�U�������܂��B�@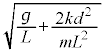 ......[�V]
......[�V] ���D��蕶�́u�����p�U����ω�ŒP�U��������ʂȏ�ԁv���Ђ�������̂ŁA��L�ł͖�蕶�̎w���ʂ�ɉ��Ă��܂���B��L�ɂ��ƁA��2�̖�蕶�ɏ�����Ă���ʂ�A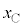 �C
�C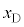 �́A
�́A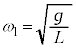 �̒P�U����
�̒P�U����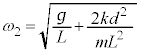 �̒P�U�����d�ˍ��킹���^�������܂��B
�̒P�U�����d�ˍ��킹���^�������܂��B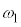 �̒P�U���̐U����
�̒P�U���̐U����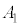 �C�����ʑ���
�C�����ʑ���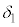 �C
�C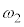 �̒P�U���̐U����
�̒P�U���̐U����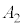 �C�����ʑ���
�C�����ʑ���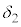 �Ƃ��āA
�Ƃ��āA �̂悤�ɂȂ�܂��B
��蕶�̎w���ʂ�ɁA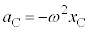 �C
�C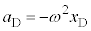 ���A�C�B�ɑ������ƁA
���A�C�B�ɑ������ƁA 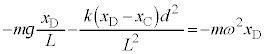 �@����C
�@����C
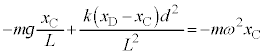 �@����D
�@����D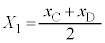 �ɂ��āA�C�{�D���A
�ɂ��āA�C�{�D���A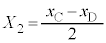 �ɂ��āA�C�|�D���A
�ɂ��āA�C�|�D���A�ƂȂ�܂����A������u2��ނ̊p�U�����v�ƌ����Ă���Ǝv���܂��B
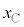 �C
�C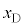 ���Ƃ��Ɋp�U����
���Ƃ��Ɋp�U����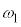 �ŒP�U������(��L����
�ŒP�U������(��L����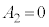 �C
�C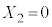 �ł�)�Ƃ��A
�ł�)�Ƃ��A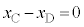 �C
�C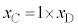 �@1 ......[�X]
�@1 ......[�X]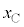 �C
�C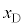 ���Ƃ��Ɋp�U����
���Ƃ��Ɋp�U����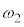 �ŒP�U������(��L���ŁC
�ŒP�U������(��L���ŁC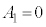 �C
�C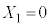 �ł�)�Ƃ��A
�ł�)�Ƃ��A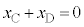 �C
�C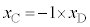
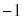 ......[�Z]
......[�Z]
��2�@[�P]���A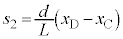 �́A�p�U����
�́A�p�U����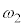 �̒P�U�������܂��B���ꂪ�A
�̒P�U�������܂��B���ꂪ�A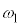 ��2�{�̊p�U�����ɂȂ�̂ŁA[�V]��[�C]�̌��ʂ�p���āA
��2�{�̊p�U�����ɂȂ�̂ŁA[�V]��[�C]�̌��ʂ�p���āA 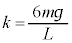 ���A
���A
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 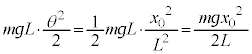 �C������̑��x��
�C������̑��x��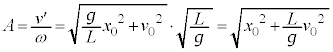 ......[�I]
......[�I]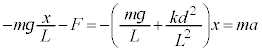 �@����@
�@����@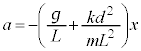
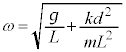 ......[�N]
......[�N]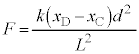 �ƍl���܂��B
�ƍl���܂��B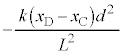 (��������)�ł��B������D�̉^���������́A�����x��
(��������)�ł��B������D�̉^���������́A�����x��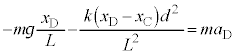 �@����A
�@����A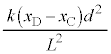 (��������)�ƁA�d�͂̉~����������
(��������)�ƁA�d�͂̉~����������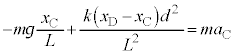 �@����B
�@����B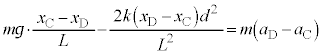 �@��
�@�� 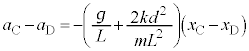
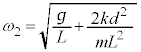 �̒P�U�������܂��B�@
�̒P�U�������܂��B�@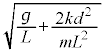 ......[�V]
......[�V]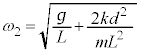 �̒P�U�����d�ˍ��킹���^�������܂��B
�̒P�U�����d�ˍ��킹���^�������܂��B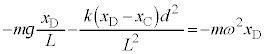 �@����C
�@����C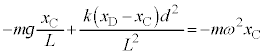 �@����D
�@����D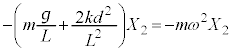 �@��
�@�� 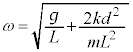 (
(