���啨��'24�N�O��[2]
���̕��͂�ǂ�ŁA�@�@�ɓK�������܂��͐��l���A{�@�@}����͓K�Ȃ��̂���I�т��̔ԍ����A���ꂼ��̉��ɋL������B�Ȃ��A�@�@�͂��ł��@�@�ŗ^����ꂽ���̂Ɠ������̂�\���B�܂��A��1�`��3�ł́A�w���ɂ��������āA�����ꂼ��̉��ɋL������B�������A�~������π�Ƃ���B
�^�̎��ԕω����Ȃ�������ł̉דd���q�̉^�����l���悤�B�דd���q�̉^���ɂ���Đ�����d��Ǝ���̉e���A����яd�͂̉e���͖������Ă悢�B
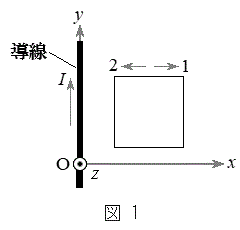 (1) �}1�̂悤�ɁAy����ɒu���ꂽ�\���ɒ���������̓����ɁAy���̐��̌����ɋ���I�̒��d��������Ă���ꍇ���l����B�^��̓�������μ�Ƃ���ƁA���̓d������鎥�����x�̑傫���́Ay�����狗��r���ꂽ�_���@�C�@�ƂȂ�Bxy���ʏ��
(1) �}1�̂悤�ɁAy����ɒu���ꂽ�\���ɒ���������̓����ɁAy���̐��̌����ɋ���I�̒��d��������Ă���ꍇ���l����B�^��̓�������μ�Ƃ���ƁA���̓d������鎥�����x�̑傫���́Ay�����狗��r���ꂽ�_���@�C�@�ƂȂ�Bxy���ʏ��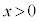 �C
�C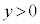 �̗̈�ɁA�����`��1�����R�C����u���B�}1�Ɏ����悤�ɁA�e�ӂ�x�����邢��y���ɕ��s�ł���B�������A�R�C���̎��ȃC���_�N�^���X�͖����ł�����̂Ƃ���B�R�C����y���̐��̌����Ɉ��̑����œ����Ƃ��A�U���d����{���F�@�}��1�̌����ɗ����@�A�}��2�̌����ɗ����@�B����Ȃ�}�B�܂��A�R�C����x���̐��̌����Ɉ��̑����œ����Ƃ��A�U���d����{�n�F�@�}��1�̌����ɗ����@�A�}��2�̌����ɗ����@�B����Ȃ�}�B
�̗̈�ɁA�����`��1�����R�C����u���B�}1�Ɏ����悤�ɁA�e�ӂ�x�����邢��y���ɕ��s�ł���B�������A�R�C���̎��ȃC���_�N�^���X�͖����ł�����̂Ƃ���B�R�C����y���̐��̌����Ɉ��̑����œ����Ƃ��A�U���d����{���F�@�}��1�̌����ɗ����@�A�}��2�̌����ɗ����@�B����Ȃ�}�B�܂��A�R�C����x���̐��̌����Ɉ��̑����œ����Ƃ��A�U���d����{�n�F�@�}��1�̌����ɗ����@�A�}��2�̌����ɗ����@�B����Ȃ�}�B
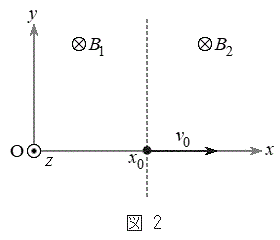 (2) ���ɁA���l�Ȏ��ꒆ�ł̉דd���q�̉^�����l���悤�B�דd���q�̑傫���͖����ł��A���̎��ʂ�m�C�d�ׂ�q(
(2) ���ɁA���l�Ȏ��ꒆ�ł̉דd���q�̉^�����l���悤�B�דd���q�̑傫���͖����ł��A���̎��ʂ�m�C�d�ׂ�q(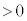 )�Ƃ���B�ȒP�̂��߁A�}2�Ɏ����悤�ȃ��f���ōl����B�����z���̕��̌����ɂ������Ă���A���̎������x�̑傫���́A����
)�Ƃ���B�ȒP�̂��߁A�}2�Ɏ����悤�ȃ��f���ōl����B�����z���̕��̌����ɂ������Ă���A���̎������x�̑傫���́A����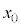 (
(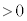 )�ɑ��āA
)�ɑ��āA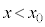 ��
��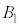 �C
�C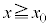 ��
��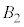 �Ƃ���B������
�Ƃ���B������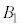 ��
��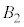 �͐��̒萔�ŁA
�͐��̒萔�ŁA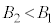 �ł���B�܂��A���q��
�ł���B�܂��A���q��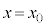 �Œ�߂��镽�ʂ�ʉ߂���Ƃ��A���̋O���͊��炩�ɂȂ���A�����͕ω����Ȃ����̂Ƃ���B
�Œ�߂��镽�ʂ�ʉ߂���Ƃ��A���̋O���͊��炩�ɂȂ���A�����͕ω����Ȃ����̂Ƃ���B����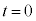 ��
��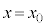 �C
�C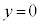 �C
�C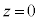 �ɂ���דd���q���Ax���̐��̌����ɑ���
�ɂ���דd���q���Ax���̐��̌����ɑ���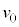 �ʼn^�����͂��߂��B�דd���q�͂܂��A
�ʼn^�����͂��߂��B�דd���q�͂܂��A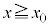 �̗̈�ɂ����ă��[�����c�͂ɂ��xy���ʓ��œ����~�^������B
�̗̈�ɂ����ă��[�����c�͂ɂ��xy���ʓ��œ����~�^������B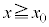 �ł̉~�O���̔��a���@�j�@�ƂȂ�B�דd���q��
�ł̉~�O���̔��a���@�j�@�ƂȂ�B�דd���q��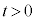 �ł͂��߂�
�ł͂��߂�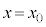 �ɓ��B����܂łɂ����鎞��
�ɓ��B����܂łɂ����鎞��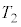 �́Am�C
�́Am�C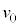 �Cq�C
�Cq�C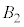 �C
�C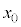 �̂����K�v�Ȃ��̂�p�����@�z�@�Ə�����B���̌�A���q��
�̂����K�v�Ȃ��̂�p�����@�z�@�Ə�����B���̌�A���q��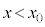 �ɂ����Ă������~�^������B
�ɂ����Ă������~�^������B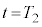 ����ӂ�����
����ӂ�����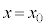 �ɓ��B����܂ł̎��Ԃ�
�ɓ��B����܂ł̎��Ԃ�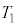 �Ƃ��A
�Ƃ��A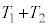 ���^���̎����Ƃ���B
���^���̎����Ƃ���B
��1�@����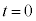 ���玞��
���玞��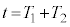 �܂ł̉דd���q��xy���ʓ��ł̋O����`���A����
�܂ł̉דd���q��xy���ʓ��ł̋O����`���A����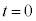 �C
�C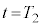 �C
�C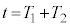 �ɂ�����ʒu�������B�܂��A����
�ɂ�����ʒu�������B�܂��A����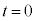 �ł̈ʒu���n�_�Ƃ��A
�ł̈ʒu���n�_�Ƃ��A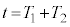 �ł̈ʒu���I�_�Ƃ���x�N�g���ɂ��āA���̑傫������B���̃x�N�g���ŕ\�����ړ����h���t�g�Ƃ�ԁB
�ł̈ʒu���I�_�Ƃ���x�N�g���ɂ��āA���̑傫������B���̃x�N�g���ŕ\�����ړ����h���t�g�Ƃ�ԁB
��1�ōl�@�����h���t�g�ɂ��āA���̕��ς̑��������߂悤�B�������x�̑傫���𐳂̒萔a�����d(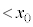 )��p����
)��p����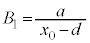 �C
�C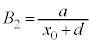 �Ɨ^����B�^���̎���
�Ɨ^����B�^���̎���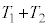 ��m�C
��m�C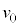 �Cq�Ca�Cd�C
�Cq�Ca�Cd�C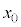 �̂����K�v�Ȃ��̂�p���ď������@�w�@�ƂȂ�B�h���t�g�̕��ς̑����́A�h���t�g��\���x�N�g���̑傫���������Ŋ��邱�Ƃɂ���ċ��߂��Am�C
�̂����K�v�Ȃ��̂�p���ď������@�w�@�ƂȂ�B�h���t�g�̕��ς̑����́A�h���t�g��\���x�N�g���̑傫���������Ŋ��邱�Ƃɂ���ċ��߂��Am�C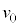 �Cq�Ca�Cd�C
�Cq�Ca�Cd�C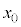 �̂����K�v�Ȃ��̂�p�����@�g�@�Ə�����B��ʂɁA��l�łȂ����ꂪ����ꍇ�ɂ��̂悤�ȃh���t�g�������A����͎�����z�h���t�g�Ƃ���B
�̂����K�v�Ȃ��̂�p�����@�g�@�Ə�����B��ʂɁA��l�łȂ����ꂪ����ꍇ�ɂ��̂悤�ȃh���t�g�������A����͎�����z�h���t�g�Ƃ���B 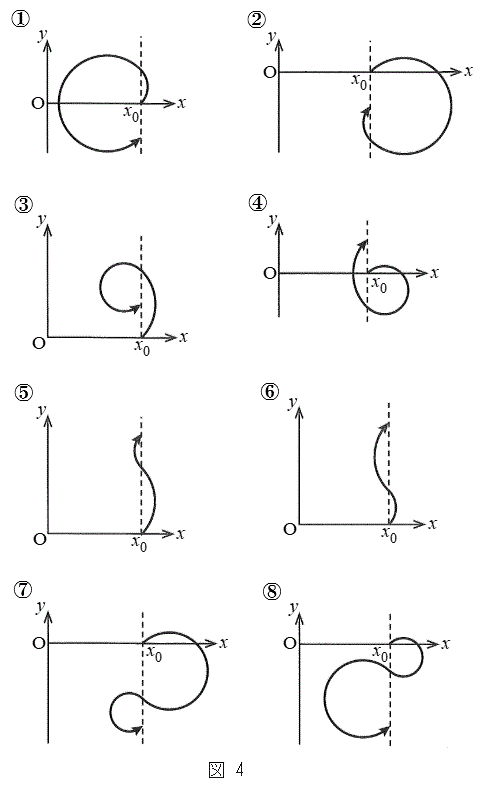 ��2�@
��2�@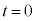 ����A
����A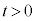 ��2��ڂ�
��2��ڂ�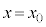 �ɒB����Ƃ��܂ł̗��q�̋O���Ƃ��čł��K���Ȃ��̂�}4�̇@�`�G�̂�������I�сA�ԍ�����B
�ɒB����Ƃ��܂ł̗��q�̋O���Ƃ��čł��K���Ȃ��̂�}4�̇@�`�G�̂�������I�сA�ԍ�����B
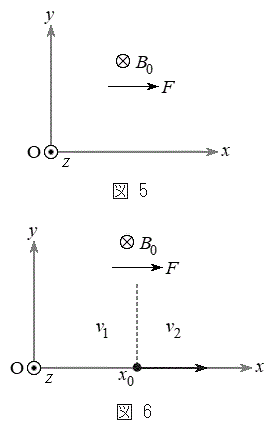 (3) ���ɁA��l�Ȏ���̂��Ƃ��A���[�����c�͂ɉ����ĊO�͂��דd���q�ɂ͂��炭�ꍇ���l���悤�B�דd���q�͎���m�C�d��q(
(3) ���ɁA��l�Ȏ���̂��Ƃ��A���[�����c�͂ɉ����ĊO�͂��דd���q�ɂ͂��炭�ꍇ���l���悤�B�דd���q�͎���m�C�d��q(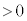 )�������A�傫���͖����ł���Ƃ���B�}5�̂悤�ɁAz���̕��̌����̈�l�Ȏ��ꂪ����A�������x�̑傫���𐳂̒萔
)�������A�傫���͖����ł���Ƃ���B�}5�̂悤�ɁAz���̕��̌����̈�l�Ȏ��ꂪ����A�������x�̑傫���𐳂̒萔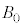 �Ƃ���B����ɁA���q�ɂ�x���̐��̌����ɑ傫��F�̈�l�ȕۑ��͂ł���O�͂���p����B���ꂨ��ъO�͂͂���������ԕϓ����Ȃ��B
�Ƃ���B����ɁA���q�ɂ�x���̐��̌����ɑ傫��F�̈�l�ȕۑ��͂ł���O�͂���p����B���ꂨ��ъO�͂͂���������ԕϓ����Ȃ��B���̂Ƃ��A�דd���q��x�������ɂ͈��͈̔͂Ŏ����I�ɐU������B�^�����̂��鎞���ŗ��q���Ax���ŏ��l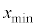 �ƂȂ�ʒu�ɂ��葬��
�ƂȂ�ʒu�ɂ��葬��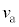 �������Ă����Ƃ���ƁAx���ő�l
�������Ă����Ƃ���ƁAx���ő�l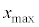 �ƂȂ�ʒu�܂ňړ������Ƃ��̑���
�ƂȂ�ʒu�܂ňړ������Ƃ��̑���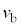 �́A���̊ԂɊO�͂������d��
�́A���̊ԂɊO�͂������d��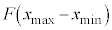 �����ł��邽��
�����ł��邽��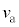 ���傫���Ȃ�B���̌�
���傫���Ȃ�B���̌�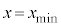 �ɂ��ǂ����Ƃ��A���q�̑�����
�ɂ��ǂ����Ƃ��A���q�̑�����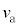 �ɔ�ׂ�{�`�F�@�傫���Ȃ�@�A�������Ȃ�@�B�ω����Ȃ�}�B
�ɔ�ׂ�{�`�F�@�傫���Ȃ�@�A�������Ȃ�@�B�ω����Ȃ�}�B
���[�����c�͂ɑ��ĊO�͂��\���Ɏア�Ƃ��A�דd���q�̉^���̓����~�^������̂���͂킸���ł���B�ȉ��ł́A�}6�̂悤�ɁA(2)�Ɠ��l��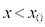 �̗̈��
�̗̈��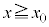 �̗̈�ɕ����A���̗��q�̉^�����Axy���ʓ��̂��ꂼ��̗̈�ŁA�قȂ鑬���œ����~�^�����郂�f���ōl�@�����B
�̗̈�ɕ����A���̗��q�̉^�����Axy���ʓ��̂��ꂼ��̗̈�ŁA�قȂ鑬���œ����~�^�����郂�f���ōl�@�����B
�דd���q�͎���ɂ�郍�[�����c�͂������A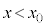 �ő���
�ő���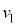 �C
�C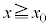 �ő���
�ő���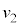 �̓����~�^�����s���Ƃ���B�����ŁA
�̓����~�^�����s���Ƃ���B�����ŁA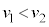 �ł���B�O�͂ɂ��
�ł���B�O�͂ɂ��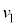 ��
��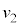 �̍��������A����ȊO�ɂ͊O�͂ɂ��^���ւ̉e���͂Ȃ��Ɖ��肷���B�܂��A
�̍��������A����ȊO�ɂ͊O�͂ɂ��^���ւ̉e���͂Ȃ��Ɖ��肷���B�܂��A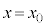 �ŗ��q�̋O���͊��炩�ɂȂ���Ƃ���B�������A��
�ŗ��q�̋O���͊��炩�ɂȂ���Ƃ���B�������A��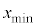 �����
�����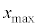 �͗p���Ȃ����ƁB
�͗p���Ȃ����ƁB
����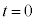 ��
��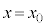 �C
�C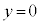 �C
�C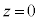 �ɂ���דd���q��x���̐��̌����ɑ���
�ɂ���דd���q��x���̐��̌����ɑ���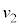 �œ����~�^�����͂��߂��B
�œ����~�^�����͂��߂��B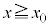 �ɂ����铙���~�^���̉~�̔��a���@���@�ƂȂ�A����
�ɂ����铙���~�^���̉~�̔��a���@���@�ƂȂ�A����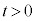 ��2��ڂ�
��2��ڂ�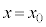 �ɒB����܂ł̎���T���@�k�@�ƂȂ�B����
�ɒB����܂ł̎���T���@�k�@�ƂȂ�B����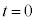 �ł̗��q�̈ʒu���n�_�A
�ł̗��q�̈ʒu���n�_�A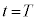 �ł̈ʒu���I�_�Ƃ���x�N�g�������̏ꍇ�̃h���t�g��\���B���̃x�N�g���̌�������Az���̕��̌����̎��ꂨ���x���̐��̌����̊O�͂ɂ����{���F�@x���̐��@�Ay���̐��@�Bx���̕��@�Cy���̕�}�̌����Ƀh���t�g���邱�Ƃ��킩��B���̃h���t�g�̕��ς̑����́A���̃x�N�g���̑傫��������T�Ŋ���AT��p�������@���@�Ƌ��߂���B���̃��f���ł́A
�ł̈ʒu���I�_�Ƃ���x�N�g�������̏ꍇ�̃h���t�g��\���B���̃x�N�g���̌�������Az���̕��̌����̎��ꂨ���x���̐��̌����̊O�͂ɂ����{���F�@x���̐��@�Ay���̐��@�Bx���̕��@�Cy���̕�}�̌����Ƀh���t�g���邱�Ƃ��킩��B���̃h���t�g�̕��ς̑����́A���̃x�N�g���̑傫��������T�Ŋ���AT��p�������@���@�Ƌ��߂���B���̃��f���ł́A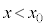 ��
��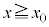 �̊e�̈�ɂ�����~�^���̔��a�����ꂼ��
�̊e�̈�ɂ�����~�^���̔��a�����ꂼ��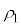 �C
�C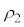 �Ƃ���ƁA���q��x��������
�Ƃ���ƁA���q��x��������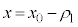 ��
��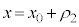 �̊Ԃ��ړ�����B
�̊Ԃ��ړ�����B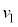 ��
��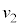 �̈Ⴂ�ɂ��^���G�l���M�[�̍���
�̈Ⴂ�ɂ��^���G�l���M�[�̍���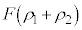 �ɓ������Ƃ���ƁA�@���@�́Am�Cq�CF�C
�ɓ������Ƃ���ƁA�@���@�́Am�Cq�CF�C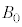 �C
�C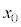 �̂����K�v�Ȃ��̂�p�����@���@�ƕ\�����Ƃ��ł���B
�̂����K�v�Ȃ��̂�p�����@���@�ƕ\�����Ƃ��ł���B
��3�@��l�ȊO�͂�����E�̓d��ɂ��͂̏ꍇ�A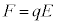 �Ƃ��āA�@���@�̃h���t�g�̕��ς̑��������߂�B�܂��A����
�Ƃ��āA�@���@�̃h���t�g�̕��ς̑��������߂�B�܂��A����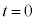 ����
����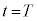 �܂ł̉דd���q��xy���ʓ��ł̋O����`���B����ɁA�����O���t�ɓd�ׂ�
�܂ł̉דd���q��xy���ʓ��ł̋O����`���B����ɁA�����O���t�ɓd�ׂ�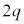 �̏ꍇ�̋O����2�������`���B�������A�ǂ����
�̏ꍇ�̋O����2�������`���B�������A�ǂ����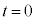 �ɂ����ď�̏����ʼn^�����͂��߂���̂Ƃ���B���ꂼ��̋O���ɓd�ׂ̒l�L���A�n�_�ƏI�_�̈Ⴂ���킩��悤�ɕ`�����ƁB
�ɂ����ď�̏����ʼn^�����͂��߂���̂Ƃ���B���ꂼ��̋O���ɓd�ׂ̒l�L���A�n�_�ƏI�_�̈Ⴂ���킩��悤�ɕ`�����ƁB
�����ł͊ȒP�ȃ��f���ɂ���čl�@�������A���m�ȃh���t�g�̑������@���@�̒萔�{�ł���A���̂悤�ȊȒP�ȃ��f���ł��A�h���t�g�̓����邱�Ƃ��ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�{��ł́A���l�Ȏ��ꒆ�A�܂��A�O�͂����݂����l�Ȏ��ꒆ�ʼnדd���q�̉^�����l����̂ł����A��蕶�������������̂��T������ǂ�ł��Ȃ��Ȃ����߂܂���B�ł����A�U���ʂ�ɐi�߂A���邱�Ǝ��͓̂������܂���B
�E�˂��̖@�����A����̌����́A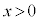 �̕�����z���������ł��B
�̕�����z���������ł��B
�R�C����y�������ɓ������Ă��A�R�C�����т������ɕω��͂Ȃ��A�R�C���ɋN�d�͂͐����܂���B����āA�U���d���͗���܂���B�@�B ......[��]�R�C����x���̐��̌����ɓ����ƁA[�C]�Ɍ���悤�ɁAr����Ŏ������x�͎���ɏ������Ȃ�̂ŁA�R�C�����т��������������Az���������̎����������悤�Ƃ�������ɋN�d�͂�����(�����c�̖@�����Q��)���A�U���d���͐}��1�̌����ɗ���܂��B�@�@ ......[�n]
(2) �������x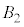 �̎��ꒆ�𑬂�
�̎��ꒆ�𑬂�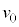 �ʼn^������דd���qq�ɓ������[�����c���̑傫����
�ʼn^������דd���qq�ɓ������[�����c���̑傫����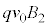 �ł�(�����́A���x�x�N�g�����v����
�ł�(�����́A���x�x�N�g�����v����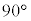 ��]����������)�B���ꒆ�a
��]����������)�B���ꒆ�a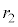 �������~�^������דd���q�̉����x��
�������~�^������דd���q�̉����x��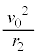 �ŁA�דd���q���^���������́A
�ŁA�דd���q���^���������́A 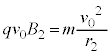 �@��
�@�� 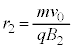 ......[�j]
......[�j]�דd���q��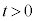 �ł͂��߂�
�ł͂��߂�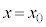 �ɓ��B����܂łɂ����鎞��
�ɓ��B����܂łɂ����鎞��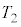 �́A�~�̔����̒���
�́A�~�̔����̒���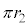 �𑬂�
�𑬂�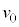 �Œʉ߂��鎞�ԂŁA
�Œʉ߂��鎞�ԂŁA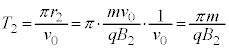 ......[�z]���l�ɂ��āA
......[�z]���l�ɂ��āA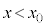 �̕����ɓ������ȍ~�̓����~�^���̔��a��
�̕����ɓ������ȍ~�̓����~�^���̔��a��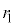 �Ƃ��āA�^���������́A
�Ƃ��āA�^���������́A 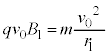 �@��
�@�� 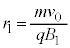 �@����@
�@����@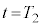 ����ӂ�����
����ӂ�����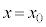 �ɓ��B����܂ł̎���
�ɓ��B����܂ł̎���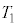 ��[�z]�Ɠ��l�ɁA
��[�z]�Ɠ��l�ɁA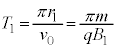
�^���̎����́A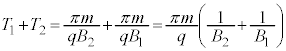 �@����A
�@����A
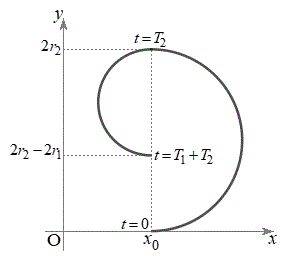 ��1
��1 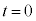 �ɓ_
�ɓ_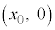 ���o�������דd���q�́A
���o�������דd���q�́A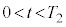 �ɂ�����
�ɂ�����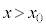 �̕����Ŕ��a
�̕����Ŕ��a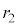 �̓����~�^���ʼn~�������
�̓����~�^���ʼn~�������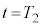 �ɓ_
�ɓ_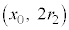 ([�j]���
([�j]���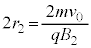 )�ɓ��B���A
)�ɓ��B���A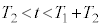 �ɂ�����
�ɂ�����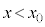 �̕����Ŕ��a
�̕����Ŕ��a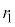 �̓����~�^���Ŕ��������
�̓����~�^���Ŕ��������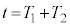 �ɓ_
�ɓ_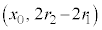 �ɓ��B���܂��B�דd���q�̋O���͉E�}�B
�ɓ��B���܂��B�דd���q�̋O���͉E�}�B����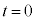 �ł̈ʒu���n�_�Ƃ��A
�ł̈ʒu���n�_�Ƃ��A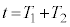 �ł̈ʒu���I�_�Ƃ���x�N�g���̑傫���́A[�j]�Ƈ@���A
�ł̈ʒu���I�_�Ƃ���x�N�g���̑傫���́A[�j]�Ƈ@���A 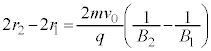 ......[��]
......[��]
�^���̎����́A�A���A
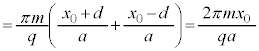 ......[�w]
......[�w]������A�h���t�g�̕��ς̑����́A
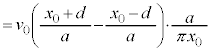
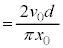 ......[�g]
......[�g]
��2�@[�j]���A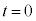 ��
��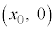 ���o�������דd���q�́A
���o�������דd���q�́A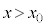 �̗̈���t���~���O����̖@����荶��������͂��Ĕ��a
�̗̈���t���~���O����̖@����荶��������͂��Ĕ��a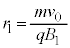 �̓����~�^�����n�߁A�₪��
�̓����~�^�����n�߁A�₪��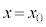 �ɓ��B���܂��B���̂Ƃ��A
�ɓ��B���܂��B���̂Ƃ��A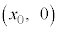 ��������̓_����������ɑ���
��������̓_����������ɑ���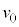 �Œʉ߂��A
�Œʉ߂��A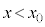 �̗̈�ɓ��荶���������͂��ć@��蔼�a
�̗̈�ɓ��荶���������͂��ć@��蔼�a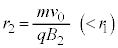 (
(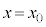 �@��
�@�� 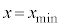 )�̓����~�^�����n�߁A�₪��
)�̓����~�^�����n�߁A�₪��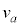 �ɓ��B���܂��B���̂悤�ȋO���́A�B ......[��]
�ɓ��B���܂��B���̂悤�ȋO���́A�B ......[��]
(3) �O��F��x���������ɓ����ۑ����Ȃ̂ŁA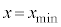 ���o�������Ƃ��̑�����
���o�������Ƃ��̑�����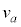 �ł���A���̈ʒu
�ł���A���̈ʒu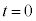 �ɖ߂����Ƃ��̗��q�̑�����
�ɖ߂����Ƃ��̗��q�̑�����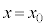 �ɖ߂�܂��B�@�B ......[�`]
�ɖ߂�܂��B�@�B ......[�`] 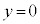 ��
��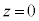 �C
�C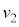 �C
�C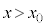 �ɂ����דd���q��x�����̌����ɑ���
�ɂ����דd���q��x�����̌����ɑ���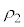 ��
��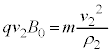 �ɂ����ē����~�^�����n�߂�ƁA���̔��a��
�ɂ����ē����~�^�����n�߂�ƁA���̔��a��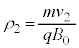 �Ƃ��āA�^���������́A�O�͂����[�����c�͂ɑ��ď[���Ɏア�Ƃ��āA(1)�Ɠ��l�ɁA
�Ƃ��āA�^���������́A�O�͂����[�����c�͂ɑ��ď[���Ɏア�Ƃ��āA(1)�Ɠ��l�ɁA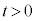 �@��
�@�� 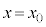 ......[��]
......[��]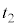 ��1��ڂ�
��1��ڂ�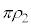 �ɓ��B����܂ł̎���
�ɓ��B����܂ł̎���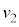 �́A�����̒���
�́A�����̒���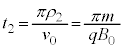 �𑬂�
�𑬂�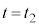 �Œʉ߂��鎞�ԂŁA
�Œʉ߂��鎞�ԂŁA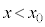 �@����B
�@����B
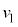 �ȍ~�A��������
�ȍ~�A��������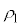 �ɓ���A����
�ɓ���A����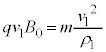 �Ŕ��a
�Ŕ��a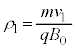 �̓����~�^��������Ƃ��āA�^���������́A
�̓����~�^��������Ƃ��āA�^���������́A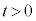 �@��
�@�� 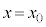 �@����C
�@����C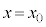 ��1��ڂ�
��1��ڂ�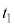 �ɓ��B���Ă���2��ڂ�
�ɓ��B���Ă���2��ڂ�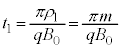 �ɓ��B����܂ł̎���
�ɓ��B����܂ł̎���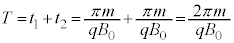 �͇B���Ɠ��l�ɁA
�͇B���Ɠ��l�ɁA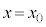 �C����Ă���ƇB���A
�C����Ă���ƇB���A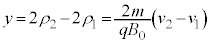 ......[�k]
......[�k]2��ڂ�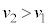 �ɓ��B�����Ƃ��A�דd���q��y���W�́A
�ɓ��B�����Ƃ��A�דd���q��y���W�́A 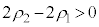 �@����D
�@����D��蕶���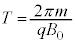 ��
��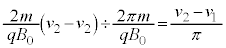 �Ȃ̂ŁA�h���t�g�̌�����y���������ł��B�@�A ......[��]�h���t�g�̕��ς̑����́A�h���t�g�̑傫���D��[�k]��
�Ȃ̂ŁA�h���t�g�̌�����y���������ł��B�@�A ......[��]�h���t�g�̕��ς̑����́A�h���t�g�̑傫���D��[�k]��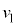 �Ŋ���A
�Ŋ���A 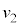 ......[��]
......[��]�� 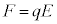 ����āA�h���t�g�̕��ς̑���[��]�́A
����āA�h���t�g�̕��ς̑���[��]�́A 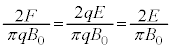 ......[��]
......[��]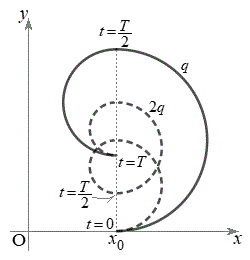 ��3�@[��]�ɂ�����
��3�@[��]�ɂ�����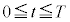 �Ƃ��āA�h���t�g�̕��ς̑����́A
�Ƃ��āA�h���t�g�̕��ς̑����́A
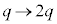 ......[��]
......[��]�ƂȂ�A�דd���q�̓d��q�C�����Ɉˑ����Ȃ��Ȃ�܂��B�d�ׂ�q�̏ꍇ��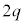 �ɂ�����O���́A��1�Ɠ��l�ɁA�E�}�����̂悤�ɂȂ�܂��B[�k]��
�ɂ�����O���́A��1�Ɠ��l�ɁA�E�}�����̂悤�ɂȂ�܂��B[�k]��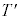 �Ƃ��邱�Ƃɂ��A�d�ׂ�
�Ƃ��邱�Ƃɂ��A�d�ׂ�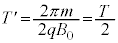 �̏ꍇ�̎���
�̏ꍇ�̎���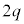 �́A
�́A �ƂȂ�܂��B�d�ׂ�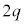 �̏ꍇ�̏ꍇ��2�������̎��Ԃ�
�̏ꍇ�̏ꍇ��2�������̎��Ԃ�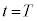 �ł��B�h���t�g�̕��ς̑����͓d�ׂɈˑ����Ȃ��̂ŁA�d�ׂ�
�ł��B�h���t�g�̕��ς̑����͓d�ׂɈˑ����Ȃ��̂ŁA�d�ׂ�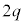 �̏ꍇ��2�������̃h���t�g�̑傫���́A�d�ׂ�q�̏ꍇ��1�������̃h���t�g�̑傫���Ɉ�v���A
�̏ꍇ��2�������̃h���t�g�̑傫���́A�d�ׂ�q�̏ꍇ��1�������̃h���t�g�̑傫���Ɉ�v���A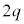 �ɂ����ēd�ׂ�q�̏ꍇ�̓��B�_�Ɠ���̓_�ɓ��B���܂��B����ēd��
�ɂ����ēd�ׂ�q�̏ꍇ�̓��B�_�Ɠ���̓_�ɓ��B���܂��B����ēd��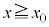 �̋O���͉E�}�_���̂悤�ɂȂ�܂��B
�̋O���͉E�}�_���̂悤�ɂȂ�܂��B
�d�ׂ�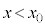 �̏ꍇ�̓����~�^���̔��a�́A
�̏ꍇ�̓����~�^���̔��a�́A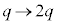 �ɂ����Ă�[��]�C
�ɂ����Ă�[��]�C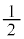 �ɂ����Ă͇C���ɂ����āA
�ɂ����Ă͇C���ɂ����āA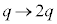 �Ƃ���ƁA�d�ׂ�q�̏ꍇ��[��]�y�чC��
�Ƃ���ƁA�d�ׂ�q�̏ꍇ��[��]�y�чC��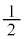 �ɂȂ�܂��B
�ɂȂ�܂��B
�Q�l�D�n����C���`�����钂�f��_�f�̌��q�́A���q�j���d�q�𑩔����Ă����Ԃɂ���d�C��ʂ��Ȃ��̂ł����A�����ɂȂ�Ɠd�q�����q�j�𗣂�ēd�q�ƃC�I�������R�ɔ�ь�����ԂɂȂ�d�C��ʂ��悤�ɂȂ�܂��B������v���Y�}�ƌ����܂����A�����d�C��ʂ��̂́A�ϗ��_�̌������㏸�C�����Ńv���Y�}�ƂȂ����C�̒���d�C���ʂ邩��ł��B
���z�́A�����̐��f��w���E�����d�����ċ���ȃv���Y�}�̉�ƂȂ������̂ł��B���z�\�ʂŃt���A�ƌĂ�锚�����ۂ��N����ƁA���z����v���Y�}���n���ɔ��n����C���̌��q�ƏՓ˂��Ėk�Ɍ���Ɍ���(�n�����n���C�������Ă��邽�߂ł�)�I�[�����������܂��B����������Ă���2024�N5�����{�ɂ��A���z�ő�K�͂ȃt���A���A�����Ĕ������A��ܓx�̖{�B�ł��I�[���������邱�Ƃ��ł��������ł��B
�v���Y�}�͑�ʂ̃C�I�����W�c�ōs�����邱�Ƃɂ��A�l�X�ȕ������ۂ��N�����܂����A�l�����z�ƌ�����j�Z�����d�����̈�ł��B���d�ׂ������f���q�j���m���Փ˂����Ċj�Z�����N�����̂ɏ[���ȉ^���G�l���M�[�������߂ɂ́A�v���Y�}��1���x�ȏ�̉��x�ɂ���K�v������ƌ����Ă��܂��B
�v���Y�}�̋�������͂���ƁA�d��������ăv���Y�}�Ƀh���t�g�^��������Ƃ��A�h���t�g���x�͉דd���q�̓d�ׂ⑬�x�Ɉˑ����Ȃ��Ȃ�܂��B������ȒP�ȃ��f����p���Ċm���߂悤�Ƃ����̂��A�{��̖�3�ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 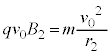 �@��
�@�� 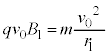 �@��
�@�� 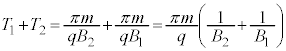 �@����A
�@����A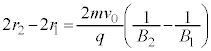 ......[��]
......[��]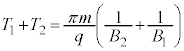
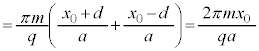 ......[�w]
......[�w]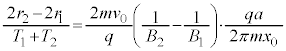
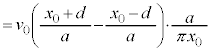
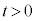 �@��
�@�� 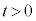 �@��
�@��