���啨��'24�N�O��[3]
���̕��͂�ǂ�ŁA�@�@�ɓK�������܂��͐��l���A{�@�@}����͓K�Ȃ��̂���I�т��̔ԍ����A���ꂼ��̉��ɋL������B�Ȃ��A�@�@�͂��ł��@�@�ŗ^����ꂽ���̂Ɠ������̂�\���B�܂��A��1�ł́A�w���ɂ��������āA�����ɋL������B�������A�~������π�Ƃ���B
�������������i�ނƂ��̂ӂ�܂����l���A��������p�������t�@�C�o�[�Ȃǂɂ��čl�@���悤�B�ȉ��ł͋�C�̋��ܗ���1�Ƃ���B
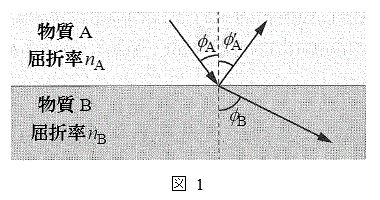 (1) �}1�̂悤�ɋ��ܗ���
(1) �}1�̂悤�ɋ��ܗ���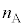 �̕���A�Ƌ��ܗ���
�̕���A�Ƌ��ܗ���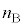 �̕���B������ȖʂŐڂ��Ă���A
�̕���B������ȖʂŐڂ��Ă���A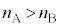 �Ƃ���BA����B�������˂����Ƃ��A���E�ʂ̖@���ɑ���p�x�Ƃ��āA���ˊp
�Ƃ���BA����B�������˂����Ƃ��A���E�ʂ̖@���ɑ���p�x�Ƃ��āA���ˊp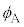 �C���ˊp
�C���ˊp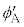 �C���܊p
�C���܊p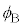 ���߂�B
���߂�B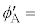 �@���@�ł���A
�@���@�ł���A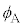 �C
�C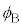 �C
�C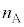 �C
�C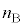 �̊W��
�̊W��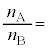 �@���@�ƂȂ�B
�@���@�ƂȂ�B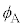 ������l
������l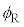 ���傫���Ƃ��A���͋��E�ʂőS���˂����B
���傫���Ƃ��A���͋��E�ʂőS���˂����B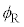 ��
��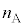 �C
�C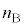 �̊W��
�̊W��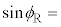 �@���@�ł���B
�@���@�ł���B
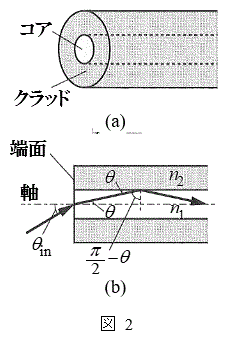 (2) ���t�@�C�o�[�́A�}2(a)�̂悤�ɋ��ܗ��̈قȂ�K���X����̍א��ɂ������̂ł���B���S�������R�A�A�O���������N���b�h�Ƃ�ԁB�R�A�ƃN���b�h�̋��ܗ������ꂼ��
(2) ���t�@�C�o�[�́A�}2(a)�̂悤�ɋ��ܗ��̈قȂ�K���X����̍א��ɂ������̂ł���B���S�������R�A�A�O���������N���b�h�Ƃ�ԁB�R�A�ƃN���b�h�̋��ܗ������ꂼ��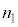 (
(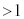 )�C
)�C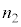 (
(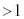 )�Ƃ���B�܂��A�R�A�̎����܂ޕ��ʓ���i�ތ����l����B
)�Ƃ���B�܂��A�R�A�̎����܂ޕ��ʓ���i�ތ����l����B���ܗ��̊W��{���F�@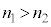 �C�A
�C�A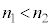 �C�B
�C�B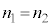 }�ŁA����ɃR�A���Ō��̐i�ޕ����ƌ��t�@�C�o�[�̎������̂Ȃ��p�xθ������p�x
}�ŁA����ɃR�A���Ō��̐i�ޕ����ƌ��t�@�C�o�[�̎������̂Ȃ��p�xθ������p�x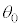 ��菬������A�}2(b)�̂悤�Ɍ��̓R�A�ƃN���b�h�̋��E�őS���˂����B(1)�ł̋c�_���ӂ܂���ƁA
��菬������A�}2(b)�̂悤�Ɍ��̓R�A�ƃN���b�h�̋��E�őS���˂����B(1)�ł̋c�_���ӂ܂���ƁA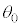 ��
��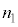 �����
�����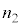 �̊W��
�̊W��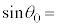 �@���@�ƂȂ�B���̂悤�Ɍ����R�A�ƃN���b�h�̋��E�ʂőS���˂���邽�߂ɂ́A���t�@�C�o�[�̒[�ʂɂ����ċ�C������R�A�Ɍ������˂���ۂɁA�������ɑ�����̓��ˊp
�@���@�ƂȂ�B���̂悤�Ɍ����R�A�ƃN���b�h�̋��E�ʂőS���˂���邽�߂ɂ́A���t�@�C�o�[�̒[�ʂɂ����ċ�C������R�A�Ɍ������˂���ۂɁA�������ɑ�����̓��ˊp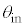 ��������������K�v������B���̏������A
��������������K�v������B���̏������A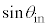 �C
�C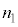 �C
�C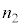 ��p���ĕ\���ƁA�@���@
��p���ĕ\���ƁA�@���@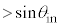 �ƂȂ�B�������A���t�@�C�o�[�̒[�ʂ͂��̎������ɑ��Đ����ł���Ƃ��A�[�ʂɂ����ăR�A�̎��ォ����˂�������l����B
�ƂȂ�B�������A���t�@�C�o�[�̒[�ʂ͂��̎������ɑ��Đ����ł���Ƃ��A�[�ʂɂ����ăR�A�̎��ォ����˂�������l����B
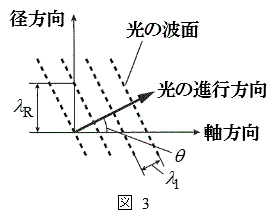 (3) ���˂����������t�@�C�o�[����i�ނ��߂ɂ́A(2)�̏��������ł͕s�\���ł���B������l�@���悤�B
(3) ���˂����������t�@�C�o�[����i�ނ��߂ɂ́A(2)�̏��������ł͕s�\���ł���B������l�@���悤�B�R�A�̎����܂ޕ��ʓ���i�ތ����l����B�}3�̂悤�ɁA�R�A���̌��̔g����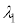 �Ƃ��A���̐i�s�����ƃR�A�̎������̂Ȃ��p�x��θ�Ƃ���B���̂Ƃ��A�a�����̔g�ʊԂ̋�����
�Ƃ��A���̐i�s�����ƃR�A�̎������̂Ȃ��p�x��θ�Ƃ���B���̂Ƃ��A�a�����̔g�ʊԂ̋�����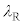 �Ƃ���ƁA
�Ƃ���ƁA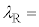 �@���@�ƂȂ��Ă���B���������āA�a�����ɂ͔g����
�@���@�ƂȂ��Ă���B���������āA�a�����ɂ͔g����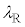 �̔g�������Ă���Ƃ݂Ȃ���B
�̔g�������Ă���Ƃ݂Ȃ���B
���a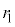 �̃R�A���Ō�����܂炸�ɐi��ł����Ƃ��A�a�����ɂ͒�ݔg���`������Ă���B�����ł́A�c�_���ȒP�ɂ��邽�߁A���R��N�ɑ��A�R�A�̒��a��
�̃R�A���Ō�����܂炸�ɐi��ł����Ƃ��A�a�����ɂ͒�ݔg���`������Ă���B�����ł́A�c�_���ȒP�ɂ��邽�߁A���R��N�ɑ��A�R�A�̒��a��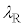 ��
��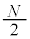 �{�ł�����̂悤�Ȓ�ݔg���`�������Ƃ���B���̂Ƃ��A
�{�ł�����̂悤�Ȓ�ݔg���`�������Ƃ���B���̂Ƃ��A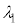 �C
�C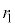 �CN��p���āA
�CN��p���āA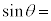 �@���@�ƕ\����B
�@���@�ƕ\����B
���ۂɌ��t�@�C�o�[���g���ۂɂ́A��C���ł̔g����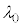 �̌��������Y���ŏW�����ăR�A�ɓ��˂����邽�߁A���͂��܂��܂�
�̌��������Y���ŏW�����ăR�A�ɓ��˂����邽�߁A���͂��܂��܂�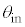 �œ��˂��A���˒����θ�͘A���I�Ȓl����������B���̂���
�œ��˂��A���˒����θ�͘A���I�Ȓl����������B���̂���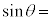 �@���@�����ƂтƂт̒l��θ�������������R�A����i�ނ��Ƃ��ł���BN�œ����Â����邱�̌������[�h�Ƃ�ԁB����A����N�̃��[�h�ɂ��āA
�@���@�����ƂтƂт̒l��θ�������������R�A����i�ނ��Ƃ��ł���BN�œ����Â����邱�̌������[�h�Ƃ�ԁB����A����N�̃��[�h�ɂ��āA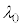 ������l
������l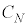 ���傫���Ƃ��A���̃��[�h�̓R�A�ƃN���b�h�̋��E�őS���˂ł����`���Ȃ��Ȃ�B
���傫���Ƃ��A���̃��[�h�̓R�A�ƃN���b�h�̋��E�őS���˂ł����`���Ȃ��Ȃ�B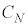 ��
��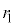 �C
�C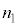 �CN�C
�CN�C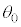 ��p���ĕ\���ƁA
��p���ĕ\���ƁA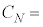 �@���@�ƂȂ�B�����ŁA
�@���@�ƂȂ�B�����ŁA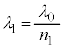 �̊W��p����B
�̊W��p����B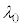 ��
��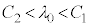 �����Ƃ��A�R�A����`������
�����Ƃ��A�R�A����`������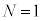 �̃��[�h�݂̂ƂȂ�B����
�̃��[�h�݂̂ƂȂ�B����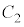 �̓J�b�g�I�t�g���Ƃ��A
�̓J�b�g�I�t�g���Ƃ��A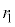 �C
�C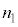 �C
�C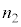 ��p�����@���@�ƕ\����B
��p�����@���@�ƕ\����B
 (4) �ȉ��ł́A
(4) �ȉ��ł́A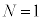 �̃��[�h�������`���ꍇ���l����B�R�A���̔g����
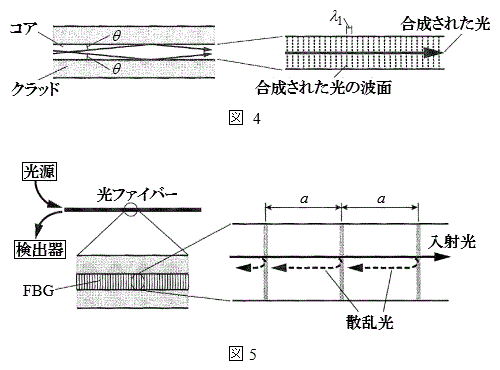
�̃��[�h�������`���ꍇ���l����B�R�A���̔g����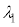 �̌��́A�}4�̂悤�Ȕg�̍����̌��ʁA�������Ɛ����Ȕg�ʂ����g�Ƃ݂Ȃ���B�܂��Aθ���������ꍇ���l���A�������ꂽ���̔g����
�̌��́A�}4�̂悤�Ȕg�̍����̌��ʁA�������Ɛ����Ȕg�ʂ����g�Ƃ݂Ȃ���B�܂��Aθ���������ꍇ���l���A�������ꂽ���̔g����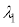 �ɓ������Ƃ���B
�ɓ������Ƃ���B�}5�̂悤�ɁA���t�@�C�o�[�̃R�A�ɁA�����U������\���������I�Ɏ������ɓ����������̂��l����B������t�@�C�o�[�E�u���b�O�E�O���[�e�B���O(FBG)�Ƃ����B���̍\���̎�����a�Ƃ���ƁAFBG�͊Ԋua�̉�܊i�q�̂悤�ɂ͂��炭�B���Ȃ킿�A���˂������̂����ꕔ���U������ē��ˑ��ւƕԂ��Ă������A��������a���ꂽ�ʒu����̎U���������ߍ����Ƃ����������Ԃ��Ă����A�}5�̌��o��Ō��o���邱�Ƃ��ł���B�������ɕԂ��Ă����������ߍ�����������A���o�ł�����̍ł������g���́Aa�C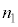 ��p����
��p����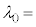 �@���@�ƕ\�����Ƃ��ł���B���o�킪���o����̂͋�C���̔g���ł��邱�Ƃɒ��ӂ���B�ȉ��ł͋��ߍ����ĕԂ��Ă������̂����g�����@���@�̌����l���A����ˌ��ƌĂԁB
�@���@�ƕ\�����Ƃ��ł���B���o�킪���o����̂͋�C���̔g���ł��邱�Ƃɒ��ӂ���B�ȉ��ł͋��ߍ����ĕԂ��Ă������̂����g�����@���@�̌����l���A����ˌ��ƌĂԁB
 (5) FBG���܂ތ��t�@�C�o�[�̈ꕔ�����l����B���ꂪ����D�̏�Ԃ���D�Ƃ���ׂď\���ɏ�������
(5) FBG���܂ތ��t�@�C�o�[�̈ꕔ�����l����B���ꂪ����D�̏�Ԃ���D�Ƃ���ׂď\���ɏ�������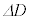 ������l�ɐL�k���A������
������l�ɐL�k���A������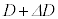 �ɂȂ�ƁAFBG�̎�����a����
�ɂȂ�ƁAFBG�̎�����a����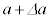 �ɕω�����B���̏ꍇ�AD�C
�ɕω�����B���̏ꍇ�AD�C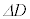 �Ca�C
�Ca�C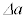 �̊W���@���@�ł���B�܂��A���̎����̕ω��ɂ��AFBG����̔��ˌ��̔g����
�̊W���@���@�ł���B�܂��A���̎����̕ω��ɂ��AFBG����̔��ˌ��̔g����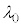 ����
����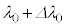 �ɕω�����B���̔g���͍����x�Ɍv���ł��邽�߁AFBG�͔����ȐL�k�����o����Z���T�[�Ƃ��ė��p�ł���B�����ŁAA��萔�Ƃ��āA
�ɕω�����B���̔g���͍����x�Ɍv���ł��邽�߁AFBG�͔����ȐL�k�����o����Z���T�[�Ƃ��ė��p�ł���B�����ŁAA��萔�Ƃ��āA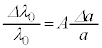 �Ƃ����BA�͐L�k�ɂƂ��Ȃ�FBG���̃R�A�̋��ܗ��̔����ȕω��̉e���Ȃǂ��܂W���ł���B
�Ƃ����BA�͐L�k�ɂƂ��Ȃ�FBG���̃R�A�̋��ܗ��̔����ȕω��̉e���Ȃǂ��܂W���ł���B
A�����肷�邽�߁A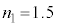 �̌��t�@�C�o�[�ɔg����
�̌��t�@�C�o�[�ɔg����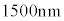 �t�߂̘A���X�y�N�g���̌������AFBG���܂ޕ����̒�����
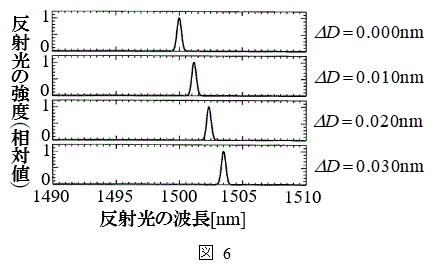
�t�߂̘A���X�y�N�g���̌������AFBG���܂ޕ����̒�����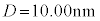 ����ω������Ȃ���AFBG����̔��ˌ��̋��x�Ɣg���̊W����C���ő��肵���B����ƁA�}6�̌��ʂ�����ꂽ�B���̌��ʂ���W��A�͗L������1����
����ω������Ȃ���AFBG����̔��ˌ��̋��x�Ɣg���̊W����C���ő��肵���B����ƁA�}6�̌��ʂ�����ꂽ�B���̌��ʂ���W��A�͗L������1����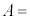 �@���@�Ƌ��߂邱�Ƃ��ł���B
�@���@�Ƌ��߂邱�Ƃ��ł���B
FBG�̉��p��̈�ɁA�M�c�����肪����B�ő̕����̒�����L�C��Ή��x��T�Ƃ���ƁA�����̕����͎����t�߂ɂ�����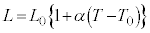 �Ƃ����W�������B�W��α�͐��c�����A
�Ƃ����W�������B�W��α�͐��c�����A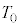 �͎����ɋ߂�����x�A
�͎����ɋ߂�����x�A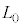 ��
��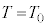 �ł̒����ł���B
�ł̒����ł���B
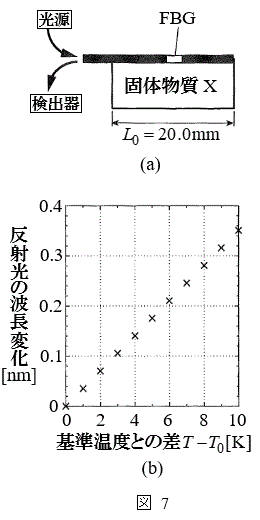 ��q��FBG���A����
��q��FBG���A����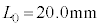 �̌ő̕���X�̎����ɐ}7(a)�̂悤�ɓ\��t�����BX�͈�l�ɔM�c�����A���t�@�C�o�[��X�̔M�c���Ɋ��S�ɒǐ����ĐL�k����Ɖ��肷��B�܂��A���x�ω��ɂ��
�̌ő̕���X�̎����ɐ}7(a)�̂悤�ɓ\��t�����BX�͈�l�ɔM�c�����A���t�@�C�o�[��X�̔M�c���Ɋ��S�ɒǐ����ĐL�k����Ɖ��肷��B�܂��A���x�ω��ɂ��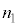 �̕ω��͔����ł���BFBG�ɋ�C���ł̔g����
�̕ω��͔����ł���BFBG�ɋ�C���ł̔g����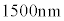 �t�߂̘A���X�y�N�g���̌�������ƁA����x�ɂ�����
�t�߂̘A���X�y�N�g���̌�������ƁA����x�ɂ�����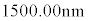 �̌������˂���A���x��ς��Ȃ��甽�ˌ��̋�C���ł̔g���̕ω��𑪒肵�����ʁA�}7(b)������ꂽ�B�������A�����̔M�c���ȊO�ɋN������g���̕ω��͍��������Ă���B�\1��X�̌�╨���Ƃ����̐��c�����ł���B
�̌������˂���A���x��ς��Ȃ��甽�ˌ��̋�C���ł̔g���̕ω��𑪒肵�����ʁA�}7(b)������ꂽ�B�������A�����̔M�c���ȊO�ɋN������g���̕ω��͍��������Ă���B�\1��X�̌�╨���Ƃ����̐��c�����ł���B
��1�@�������ʂ�A�̒l��p���AX���\1�̂ǂ̕������𐄒肹��B�c�_�̉ߒ��������B
�\1
| �@�������@ | ���c����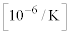 |
| ���� | 8.8 |
| �� | 18.9 |
| ���� | 30.2 |
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���t�@�C�o�[�̖��ł����A���t�@�C�o�[���������`�d���Ă����ׂ���ł͂Ȃ��A���t�@�C�o�[���ɐ݂�����FBG�ƌĂ��A����̔g���̌������ʉ߂�����悤�ɂ��邽�߂̍\�����������ł��B
(1) ���˂̖@�����A���ˊp�Ɠ��ˊp�͓������A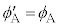 ......[��]
......[��] ���܂̖@�����A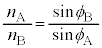 ......[��]
......[��]
[��]�ɂ����āA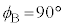 �̂Ƃ���
�̂Ƃ���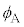 ��
��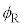 (�ՊE�p)�Ƃ��āA
(�ՊE�p)�Ƃ��āA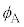 ��
��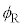 ���傫���Ƃ����͋��E�ʂ��S��������܂��B
���傫���Ƃ����͋��E�ʂ��S��������܂��B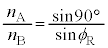 ���A
���A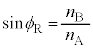 ......[��]
......[��]
(2) [��]�ɂ�����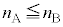 �ɂȂ��Ă��܂��ƁA�S���˂��N�������ˊp�����݂��Ȃ��Ȃ��Ă��܂��̂ŁA���t�@�C�o�[���ɂ����đS���˂𑱂��邽�߂ɂ́A�R�A�̋��ܗ����N���b�h�̋��ܗ�������K�v������܂��B����āA
�ɂȂ��Ă��܂��ƁA�S���˂��N�������ˊp�����݂��Ȃ��Ȃ��Ă��܂��̂ŁA���t�@�C�o�[���ɂ����đS���˂𑱂��邽�߂ɂ́A�R�A�̋��ܗ����N���b�h�̋��ܗ�������K�v������܂��B����āA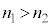 �@�@ ......[��]
�@�@ ......[��] �R�A����N���b�h�ɓ�����ɂ��ăN���b�h���̋��܊p��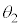 �Ƃ��āA���܂̖@�����A
�Ƃ��āA���܂̖@�����A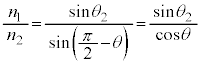
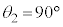 �̂Ƃ���θ��
�̂Ƃ���θ��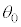 �Ƃ��āA
�Ƃ��āA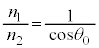
�� 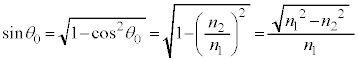 ......[��]��C������R�A�ɓ��˂���Ƃ��̋��܂̖@�����A
......[��]��C������R�A�ɓ��˂���Ƃ��̋��܂̖@�����A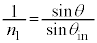
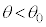 �̂Ƃ��R�A�ƃN���b�h�̋��E�ʂőS���˂���̂ŁA[��]���A
�̂Ƃ��R�A�ƃN���b�h�̋��E�ʂőS���˂���̂ŁA[��]���A 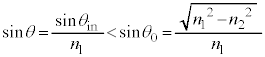 �@��
�@�� 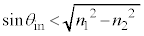 ......[��]
......[��]
(3) �}3���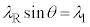 �@��
�@�� 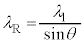 ......[��]
......[��] ������A�R�A�̒��a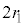 ��
��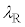 ��
��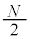 �{�ł���(���g���̐����{���}���̒����ɂȂ�B���g���Q��)���Ƃ���A
�{�ł���(���g���̐����{���}���̒����ɂȂ�B���g���Q��)���Ƃ���A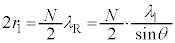
�� 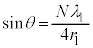 ......[��]
......[��]
(2)�̖�蕶���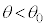 �̂Ƃ��R�A�ƃN���b�h�̋��E�ʂőS���˂���̂ŁA
�̂Ƃ��R�A�ƃN���b�h�̋��E�ʂőS���˂���̂ŁA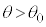 �̂Ƃ��ɂ̓R�A�ƃN���b�h�̋��E�őS���˂ł������͓`���Ȃ��Ȃ�܂��B�܂�A
�̂Ƃ��ɂ̓R�A�ƃN���b�h�̋��E�őS���˂ł������͓`���Ȃ��Ȃ�܂��B�܂�A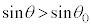 �̂Ƃ��ɑS���˂ł����`���Ȃ��Ȃ�̂ŁA�a�����ɒ�ݔg�����������[��]��
�̂Ƃ��ɑS���˂ł����`���Ȃ��Ȃ�̂ŁA�a�����ɒ�ݔg�����������[��]��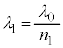 ��p���āA
��p���āA �� 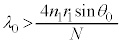 ����āA
����āA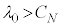 �̂Ƃ��S���˂ł����ɓ`���Ȃ��Ȃ�Ƃ��āA
�̂Ƃ��S���˂ł����ɓ`���Ȃ��Ȃ�Ƃ��āA 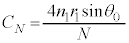 ......[��]
......[��]�����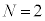 �Ƃ��āA[��]���J�b�g�I�t�g��
�Ƃ��āA[��]���J�b�g�I�t�g��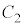 �́A
�́A 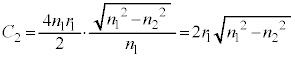 ......[��]
......[��]�R�A����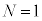 �̃��[�h�̂ݓ`���
�̃��[�h�̂ݓ`���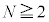 �̃��[�h���`���Ȃ������F
�̃��[�h���`���Ȃ������F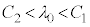 �́A
�́A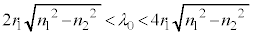 �ƂȂ�܂��B
�ƂȂ�܂��B
(4) �אڂ���u�U������\���v�������������鋗����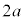 �ł��B�R�A�̋��ܗ���
�ł��B�R�A�̋��ܗ���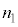 �Ȃ̂Ō��w�I������
�Ȃ̂Ō��w�I������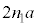 �ł��B�U�������m�����ߍ�������(���̊������Q��)�́Am�𐮐��Ƃ��āA
�ł��B�U�������m�����ߍ�������(���̊������Q��)�́Am�𐮐��Ƃ��āA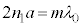 �C��������g��
�C��������g��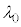 (
(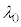 �́A��蕶�̒��ӂɂ���ʂ�A��C���̔g���ł�)�̂����A�ł��������̂́A
�́A��蕶�̒��ӂɂ���ʂ�A��C���̔g���ł�)�̂����A�ł��������̂́A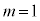 �̂Ƃ���
�̂Ƃ���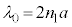 ......[��]
......[��]
(5) ���t�@�C�o�[���L�k����Ƃ��A���t�@�C�o�[�̒����̕ω��̊����ƁAFBG�̎����̕ω��̊����͓������̂ŁA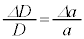 ......[��]
......[��] �}6������ƁA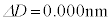 �̂Ƃ���
�̂Ƃ���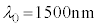 �ɂ��������ˌ����x�̔g���́A���̂���̑傫��
�ɂ��������ˌ����x�̔g���́A���̂���̑傫��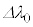 �͂ق�
�͂ق�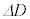 �ɔ�Ⴕ�A
�ɔ�Ⴕ�A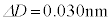 �̂Ƃ��ق�
�̂Ƃ��ق�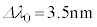 �ł��B
�ł��B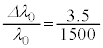 �C[��]���
�C[��]���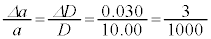
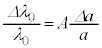 ���A
���A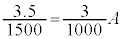
����āA�L������1���ŁA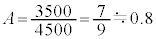 ......[��]
......[��] ���D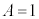 �ɂȂ�Ȃ��̂́A���t�@�C�o�[���L�k����Ƃ��A[��]�ɂ�����FBG�̎���a���ω����邾���łȂ��A���ܗ�
�ɂȂ�Ȃ��̂́A���t�@�C�o�[���L�k����Ƃ��A[��]�ɂ�����FBG�̎���a���ω����邾���łȂ��A���ܗ�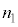 ��(�����̕ω������ł�����������)�ω����邩��ł��B
��(�����̕ω������ł�����������)�ω����邩��ł��B
�}7���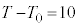 �̂Ƃ���
�̂Ƃ���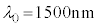 �̔��ˌ��̔g���ω�
�̔��ˌ��̔g���ω�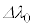 �͂��悻
�͂��悻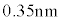 �ŁA
�ŁA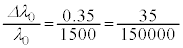
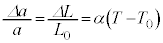 �ƌ��āA
�ƌ��āA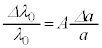 ���A
���A 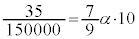 �@��
�@�� 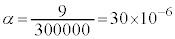
�\1�̒��ŋ߂��̂́A���� ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 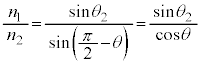
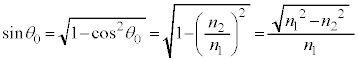 ......[��]
......[��]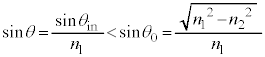 �@��
�@�� 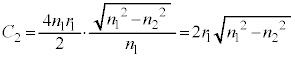 ......[��]
......[��]