�U����H�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���ȃC���_�N�^���XL���R�C�����Ód�e��C���R���f���T�[��ڑ����A�R�C�����d���𗬂�����Ԃ��A�R���f���T�[���d����~������Ԃ�����u����ƁA��H�𗬂���d���A�R���f���T�[���[���d�����U������B�U�������g��f �́A
�ŗ^������B�������g����U����H���ŗL���g���ƌ����B
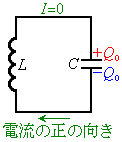 (1) �E�}�̂悤�ɁA���ȃC���_�N�^���XL�̃R�C�����Ód�e��C�̃R���f���T�[��ڑ����A�R���f���T�[���d��
(1) �E�}�̂悤�ɁA���ȃC���_�N�^���XL�̃R�C�����Ód�e��C�̃R���f���T�[��ڑ����A�R���f���T�[���d�� ��~���ĕ��u����Ƃǂ��Ȃ邩���l���܂��B
��~���ĕ��u����Ƃǂ��Ȃ邩���l���܂��B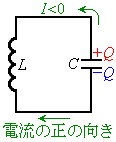 (2) ���炭����ƁA�R���f���T�[���d��������������d��������n�߂܂�(���̂Ƃ��d���͕�)�B�����d����I�C���̂Ƃ��R���f���T�[���~���Ă����d�C����Q�Ƃ���ƁA�R�C�����[���d����
(2) ���炭����ƁA�R���f���T�[���d��������������d��������n�߂܂�(���̂Ƃ��d���͕�)�B�����d����I�C���̂Ƃ��R���f���T�[���~���Ă����d�C����Q�Ƃ���ƁA�R�C�����[���d����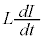 �C�R���f���T�[���[���d����
�C�R���f���T�[���[���d����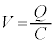 �ŁA��H���������悤�ɃL���q�z�b�t�̑�2�@����K�p����ƁA
�ŁA��H���������悤�ɃL���q�z�b�t�̑�2�@����K�p����ƁA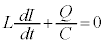 �@����@
�@����@���������܂��B
�����Ă��܂��d���͂Ȃ��A�R���f���T�[���G�l���M�[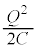 �C�R�C�����G�l���M�[
�C�R�C�����G�l���M�[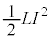 �̘a�͓����̃R���f���T�[���G�l���M�[�Ɠ����ł��B�܂�A
�̘a�͓����̃R���f���T�[���G�l���M�[�Ɠ����ł��B�܂�A 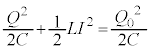 �@����A
�@����A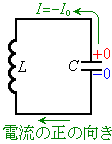 (3) �₪�āA�R���f���T�[�����d�������o���āA�R���f���T�[���d�C���̓[���ƂȂ�A�R���f���T�[���G�l���M�[���[���ɂȂ�܂��B���̎��_�ŁA�G�l���M�[�͑S�ăR�C�����G�l���M�[�ƂȂ�A���̂Ƃ����d���̐�Βl��
(3) �₪�āA�R���f���T�[�����d�������o���āA�R���f���T�[���d�C���̓[���ƂȂ�A�R���f���T�[���G�l���M�[���[���ɂȂ�܂��B���̎��_�ŁA�G�l���M�[�͑S�ăR�C�����G�l���M�[�ƂȂ�A���̂Ƃ����d���̐�Βl��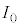 �Ƃ���(���ꂪ�d��I�̍ő�l�ɂȂ�)�ƁA
�Ƃ���(���ꂪ�d��I�̍ő�l�ɂȂ�)�ƁA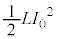 �ƂȂ�܂��B���̒l�́A�����̃R���f���T�[���G�l���M�[�ɓ������A
�ƂȂ�܂��B���̒l�́A�����̃R���f���T�[���G�l���M�[�ɓ������A���������܂��B����āA
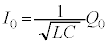 �@����B
�@����B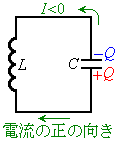 (4) �R���f���T�[���d�C�����[���ɂȂ��Ă��d�������ꑱ����̂ŁA�R���f���T�[�ɂ͓����Ƌt�������d��Q�����܂�n�߂܂��B��H�𗬂���d��I�Ƃ̊Ԃɇ@���C�A�����������܂��B����ɔ����A�d���̐�Βl���������Ă��܂��B
(4) �R���f���T�[���d�C�����[���ɂȂ��Ă��d�������ꑱ����̂ŁA�R���f���T�[�ɂ͓����Ƌt�������d��Q�����܂�n�߂܂��B��H�𗬂���d��I�Ƃ̊Ԃɇ@���C�A�����������܂��B����ɔ����A�d���̐�Βl���������Ă��܂��B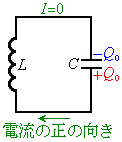 (5) �d���̐�Βl�����葱�����Ƀ[���ɂȂ�(�R�C�����G�l���M�[���[��)�ƁA�R���f���T�[���d�C����
(5) �d���̐�Βl�����葱�����Ƀ[���ɂȂ�(�R�C�����G�l���M�[���[��)�ƁA�R���f���T�[���d�C����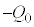 �ƂȂ�A�R���f���T�[���G�l���M�[�͓������G�l���M�[
�ƂȂ�A�R���f���T�[���G�l���M�[�͓������G�l���M�[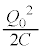 �ɖ߂�܂��B
�ɖ߂�܂��B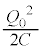 �͕ۑ�����A�R���f���T�[���d����
�͕ۑ�����A�R���f���T�[���d����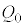 �ɂȂ�����A
�ɂȂ�����A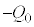 �ɂȂ����肵�Ȃ���A��L(1)�`(5)���J��Ԃ���A�d�C�I�ȐU�����ۂ������܂��B
�ɂȂ����肵�Ȃ���A��L(1)�`(5)���J��Ԃ���A�d�C�I�ȐU�����ۂ������܂��B
�ŏ��ɁA��H���d���𗬂��Ă������ꍇ���A��L�Ɠ��l�ł��B
�R���f���T�[���d�C�����A
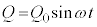 �@����C
�@����C
�̂悤�ɕω�����Ƃ��āA�d��I�́A
����āA�B���A�d���̍ő�l�ɂ��āA
�ƂȂ�A�d�C�U�������g����f �Ƃ��āA
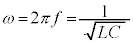 ��
�� 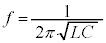
Q���C���ŕ\����闝�R���l���Ă݂܂��B
��L�̐U����H�ɂ����āA��H�𗬂���d��I�ƁA�R���f���T�[���d�C��Q�̊Ԃɂ́A�@���F
���������܂��B
L�Ŋ���ƁA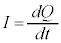 ���A
���A
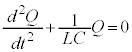 �@����D
�@����D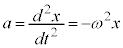 �Ɠ����`�����Ă��܂��B���Wx���D�ɂ������d�C��Q�ɒu����������`�ɂȂ��Ă��܂��B�P�U�����Ă��镨�̂̍��W
�Ɠ����`�����Ă��܂��B���Wx���D�ɂ������d�C��Q�ɒu����������`�ɂȂ��Ă��܂��B�P�U�����Ă��镨�̂̍��W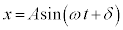 ����A
����A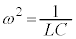 �Ƃ��āA
�Ƃ��āA
�Ə����邱�Ƃ��킩��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 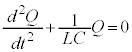 �@����D
�@����D