���H�啨��'04�N�O��[2]
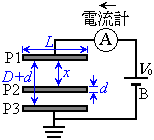 �@�}�̂悤�Ɉ��L�̐����`�Ō�����d��3���̓d�ɔ�P1�CP2�CP3������BP1�|P3�Ԃɂ͋N�d��
�@�}�̂悤�Ɉ��L�̐����`�Ō�����d��3���̓d�ɔ�P1�CP2�CP3������BP1�|P3�Ԃɂ͋N�d��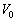 �̓d�rB���ڑ�����Ă��āAP3�͐ڒn����Ă���B3���͕̔��s�ł���BP1��P3�͌Œ肳��Ă���A���̊Ԃ̋�����
�̓d�rB���ڑ�����Ă��āAP3�͐ڒn����Ă���B3���͕̔��s�ł���BP1��P3�͌Œ肳��Ă���A���̊Ԃ̋�����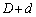 �ł���BP2�́AP1��P3�̊Ԃŏ㉺�ɓ������Ƃ��ł��AP1��P2�̊Ԋu��x�Ƃ���BP2�̓�������v�́A�\���ɂ������ł���A���̑����œd�ׂ��������Ƃɂ�蔭�����鎥�E�Ȃǂ͖����ł���قǏ������B�܂��Ԃ̋�����0�̂Ƃ��́A���m���ڐG���Ă���A�d�C�I�Ɍ݂��ɓ��d�ʂɂȂ�Ƃ���B�d�r�̓�����R�͖����ł�����̂Ƃ���B
�ł���BP2�́AP1��P3�̊Ԃŏ㉺�ɓ������Ƃ��ł��AP1��P2�̊Ԋu��x�Ƃ���BP2�̓�������v�́A�\���ɂ������ł���A���̑����œd�ׂ��������Ƃɂ�蔭�����鎥�E�Ȃǂ͖����ł���قǏ������B�܂��Ԃ̋�����0�̂Ƃ��́A���m���ڐG���Ă���A�d�C�I�Ɍ݂��ɓ��d�ʂɂȂ�Ƃ���B�d�r�̓�����R�͖����ł�����̂Ƃ���B
L��P1�|P3�Ԃ̋����ɔ�ׂď\���傫���A�d�ɊԂ͐^��ł���A���̗U�d����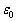 �ł���Ƃ���B
�ł���Ƃ���B
(a) �͂���P2��P1�ƐڐG(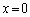 )�����Ă������A����
)�����Ă������A����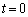 ����P3�ƐڐG���鎞��
����P3�ƐڐG���鎞��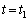 (
(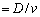 )�܂ň��̑���v��P2���������ɓ��������B
)�܂ň��̑���v��P2���������ɓ��������B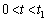 �ł�P1�̎��d��
�ł�P1�̎��d��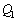 ���AP2�̓d��
���AP2�̓d��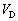 �����x�̊��Ƃ��ĕ\���B
�����x�̊��Ƃ��ĕ\���B (b) 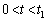 �ł�P2�̓d��
�ł�P2�̓d��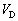 ��x�̊��Ƃ��ĕ\���B
��x�̊��Ƃ��ĕ\���B (c) ����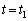 �ɂ�����P2�̉��̖ʂɂ���d�ׂ�P3�̏�̖ʂɂ���d�ׂ͑ł����������B�����Ď���
�ɂ�����P2�̉��̖ʂɂ���d�ׂ�P3�̏�̖ʂɂ���d�ׂ͑ł����������B�����Ď���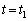 ����A�Ă�P2�����̑���v�ŏ�����ɓ������A����
����A�Ă�P2�����̑���v�ŏ�����ɓ������A����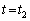 (
(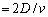 )��P1�ƍēx�ڐG�������B
)��P1�ƍēx�ڐG�������B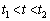 �ł�P2�̓d��
�ł�P2�̓d��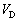 ��x�̊��Ƃ��ĕ\���B
��x�̊��Ƃ��ĕ\���B (d) 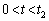 �ł�P1�̓d��
�ł�P1�̓d��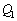 ������t�̊��Ƃ��Đ}������B
������t�̊��Ƃ��Đ}������B (e) 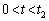 �ł�P1�̓d��
�ł�P1�̓d��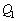 �̕ω��͓d�rB���痬�ꂱ�ޓd���ɂ��B�d���v�𗬂��d��������t�̊��Ƃ��Đ}������B�������A�d���v�̓�����R�͖����ł�����̂Ƃ���BP1�Ɍ������ė��ꍞ�ޓd���̌���(�}�̖��̌���)�𐳂̌����Ƃ���B
�̕ω��͓d�rB���痬�ꂱ�ޓd���ɂ��B�d���v�𗬂��d��������t�̊��Ƃ��Đ}������B�������A�d���v�̓�����R�͖����ł�����̂Ƃ���BP1�Ɍ������ė��ꍞ�ޓd���̌���(�}�̖��̌���)�𐳂̌����Ƃ���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�����̏�ɐ��m�Ȓl����R�����͔̂��ɓ���̂ŁAswitched capacitor(�l�b�g��Ō������Ă݂Ă�������)�Ƃ����Z�p���g���܂��B�R���f���T�[�̋ɔԓd�����X�C�b�`���O���邽�т�2���ԑQ�����ɏ]���ĕω����Ȃ�����l�ɋ߂Â��̂ŁA�������̃e�[�}�Ƃ��Ď��グ��ꂽ���Ƃ�����܂��Bswitched capacitor�ł́A��R�l�̓X�C�b�`���O�����g���Ő��m�ɐ���ł��܂��B���̖��́A�R���f���T�[�̋ɔ��ړ����x����R�l�𐳊m�ɐ���ł���ƌ����Ă���̂ŁA���J�I��switched capacitor�Ƃ������܂��B���p�I�ȉ��l������Ǝv���܂����A���̖����o�肵�����H��̐搶�́A������Ɠ����o��Ȃ����Ă���ł��傤���H
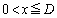 �̂Ƃ��AP1�|P2�Ԃ��Ód�e��
�̂Ƃ��AP1�|P2�Ԃ��Ód�e��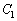 �́A
�́A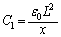
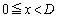 �̂Ƃ��AP2�|P3�Ԃ��Ód�e��
�̂Ƃ��AP2�|P3�Ԃ��Ód�e��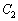 �́A
�́A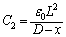
P2��P1�ɐڂ��Ă���Ƃ�(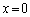 )�ɂ́AP1�{P2��P3�̊ԁA�܂��AP2��P3�ɐڂ��Ă���Ƃ�(
)�ɂ́AP1�{P2��P3�̊ԁA�܂��AP2��P3�ɐڂ��Ă���Ƃ�(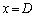 )�ɂ́AP1��P2�{P3�̊Ԃ��A�ɔԋ���D�D�ʐ�
)�ɂ́AP1��P2�{P3�̊Ԃ��A�ɔԋ���D�D�ʐ�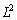 �C�����A�Ód�e��
�C�����A�Ód�e��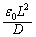 ��1�̃R���f���T�[�ɂȂ��Ă��܂��B
��1�̃R���f���T�[�ɂȂ��Ă��܂��B
(a) P1�|P2�Ԃ��d�ʍ��́A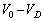
����āA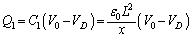 ......[��] ����@
......[��] ����@
(b) P2��P1�𗣂��u��(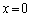 )�ɁAP2��P3�Ɍ������������ʂɂ́A���d��
)�ɁAP2��P3�Ɍ������������ʂɂ́A���d��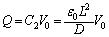 �����݂��܂��B���̂܂܁AP2��P1���痣���ƁA�����d����P2�̒��Ɏ��c����Ă��܂��܂��B���̂Ƃ��ɂ́A
�����݂��܂��B���̂܂܁AP2��P1���痣���ƁA�����d����P2�̒��Ɏ��c����Ă��܂��܂��B���̂Ƃ��ɂ́A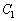 ��
��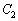 �Ƃ�Ƃ��Ĉ������Ƃ͂ł��Ȃ�(�����F
�Ƃ�Ƃ��Ĉ������Ƃ͂ł��Ȃ�(�����F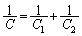 ���g���Ǝ��s����)�̂Œ��ӂ��K�v�ł��B
���g���Ǝ��s����)�̂Œ��ӂ��K�v�ł��B P2��P1��������x�̂Ƃ���ɗ����Ƃ��AP2�̉����̖ʂɌ�����d����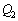 �Ƃ���ƁAP2�|P3�Ԃ��d����
�Ƃ���ƁAP2�|P3�Ԃ��d����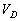 ������A
������A 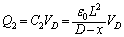 ����A
����A����AP2�̏㑤�̖ʂɒ~�����Ă����d����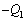 �CP2�ɂ��d��Q���c����Ă���̂ŁA
�CP2�ɂ��d��Q���c����Ă���̂ŁA 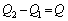 �@����B
�@����B�@�C�A��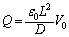 ���B�ɑ������ƁA
���B�ɑ������ƁA 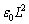 �Ŋ���A������ƁA
�Ŋ���A������ƁA��������ƁA
�� 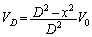 ......[��]
......[��]
(c) P2��P3�𗣂��u�ԂɁAP2��P1�Ɍ������������ʂɂ́A���d��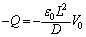 �����݂��܂��B���̂܂܁AP2��P3���痣���ƁA�����d����P2�̒��Ɏ��c����܂��B
�����݂��܂��B���̂܂܁AP2��P3���痣���ƁA�����d����P2�̒��Ɏ��c����܂��B P2��P1��������x�̂Ƃ���ɗ����Ƃ��AP2�̏㑤�̖ʂɌ�����d���͇@��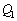 �CP2�̉����̖ʂɌ�����d���͇A��
�CP2�̉����̖ʂɌ�����d���͇A��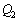 �ŗ^�����܂��BP2�ɂ́A�d��
�ŗ^�����܂��BP2�ɂ́A�d��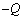 ���c����Ă���̂ŁA
���c����Ă���̂ŁA �@�C�A���A
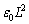 �Ŋ���A������ƁA
�Ŋ���A������ƁA��������ƁA
�� 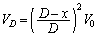 ......[��]
......[��]
(d) 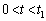 �ɂ����ẮA
�ɂ����ẮA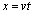
�@��(b)�̌��ʂ��A
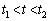 �ɂ����ẮA
�ɂ����ẮA�@��(c)�̌��ʂ��A
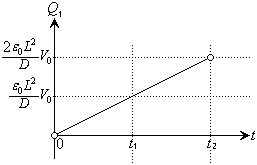
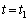 �ɂ����ẮA
�ɂ����ẮA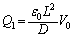 ������A
������A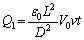 �ɂ�����
�ɂ�����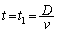 ���������l�ɂȂ��Ă��܂��B����āA
���������l�ɂȂ��Ă��܂��B����āA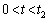 �ɂ����āA
�ɂ����āA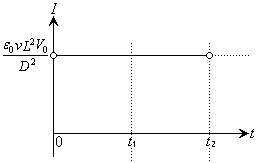
(e) 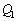 �����傷��Ƃ��d�������Ȃ̂ŁA
�����傷��Ƃ��d�������Ȃ̂ŁA
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B