�����H�Ƒ�w2012�N�O�������������
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
[1]�@���̖����ł���~�ʌ^�̃��[��ABC(���aR�C����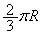 )������A�~�ʂ��܂ޖʂƏ��������ɂȂ�悤�u����Ă���B���[���̒���B�͏�ɏ��ɌŒ肳��Ă���AB��ʂ鉔����OB�����Ƃ��ă��[���͉�]���邱�Ƃ��ł���B�傫���̖����ł��镨��(����M)�́A���[������^������Ƃ��A���[���ɑ�������Ȃ���Ȃ߂炩�ɉ^�����A���[(A�CC)�ł̂݃��[�����痣��邱�Ƃ��ł���B
)������A�~�ʂ��܂ޖʂƏ��������ɂȂ�悤�u����Ă���B���[���̒���B�͏�ɏ��ɌŒ肳��Ă���AB��ʂ鉔����OB�����Ƃ��ă��[���͉�]���邱�Ƃ��ł���B�傫���̖����ł��镨��(����M)�́A���[������^������Ƃ��A���[���ɑ�������Ȃ���Ȃ߂炩�ɉ^�����A���[(A�CC)�ł̂݃��[�����痣��邱�Ƃ��ł���B
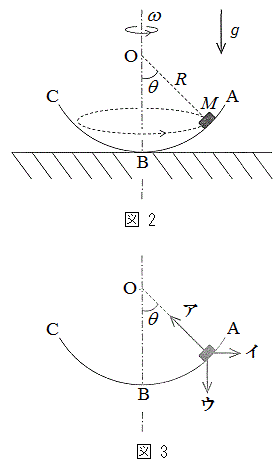
���̂��~�ʌ^���[������^������Ƃ��A�~�ʂ̒��SO���猩�āA���̂�OB�ƂȂ��p��θ �Ƃ���B�d�͉����x�̑傫����g�Ƃ��A�ȉ��̖₢�ɓ�����B
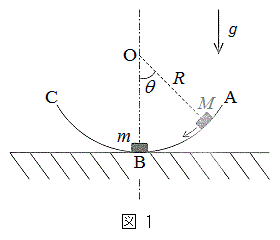
[A] ���[������]���Ă��Ȃ��Ƃ��A����M�̕��̂�A�ɏ悹�A�Â��ɗ������Ƃ���A���̂̓��[�����}1�̂悤�ɉ^�����n�߂��B
(a) ���̂��pθ (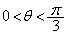 )�̈ʒu���^�����Ă���Ƃ��A���̂̑����A���[������鐂���R�͂����߂�B
)�̈ʒu���^�����Ă���Ƃ��A���̂̑����A���[������鐂���R�͂����߂�B (b) ���̂����[������^�����AB�̈ʒu�ɓ��B�����Ƃ��A���[����ŐÎ~���Ă����傫���̖����ł��镨��(����m)�ƏՓ˂����B�Փˌ�A����m�̕��̂̓��[������Ȃ߂炩�ɉ^�����A�ĂяՓ˂��邱�ƂȂ��A���[���̒[C���痣�ꂽ�B2�̕��̊Ԃ̔����W����e (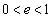 )�ł���Ƃ��A���̉^�����������邽�߂�m�̏��������߂�B
)�ł���Ƃ��A���̉^�����������邽�߂�m�̏��������߂�B
[B] OB�����ɂ��āA�~�ʌ^�̃��[����}2�̂悤�ɉ�]������B���̂Ƃ��A���[����̕���(����M)�̓��[���ƂƂ��ɉ�]�^������B
 (c) ����p���xω �Ń��[������]���A�pθ (
(c) ����p���xω �Ń��[������]���A�pθ (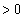 )�̈ʒu�ŕ��̂������~�^�����Ă���ꍇ�ɂ��čl����B���̉^�����A��]���Ă��郌�[����̊ϑ��҂��猩��ƁA���̂ɓ����͂͐}3�̂悤�ɂ荇���A���̂͐Î~���Č�����B���̊ϑ��҂��猩�����̂ɓ�����(�}3�F�A�C�C�C�E)�̖��̂������B�܂��A���̉^���͊p���xω ��
)�̈ʒu�ŕ��̂������~�^�����Ă���ꍇ�ɂ��čl����B���̉^�����A��]���Ă��郌�[����̊ϑ��҂��猩��ƁA���̂ɓ����͂͐}3�̂悤�ɂ荇���A���̂͐Î~���Č�����B���̊ϑ��҂��猩�����̂ɓ�����(�}3�F�A�C�C�C�E)�̖��̂������B�܂��A���̉^���͊p���xω ��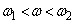 �̏��������Ƃ���������B���̂Ƃ�
�̏��������Ƃ���������B���̂Ƃ�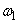 �C
�C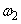 �����߂�B
�����߂�B(d) ��(c)�ɂ����āA���[���̊p���x��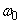 (
(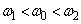 )�ɌŒ肷��B���̂Ƃ��A��]���Ă��郌�[����̊ϑ��҂��猩��ƁA�p
)�ɌŒ肷��B���̂Ƃ��A��]���Ă��郌�[����̊ϑ��҂��猩��ƁA�p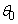 �̈ʒu�ŕ��̂ɓ����͂͂荇���A���̂͐Î~���Č�����B���ɁA���̂��荇���̈ʒu���班���������������Ƃ���A���̂̓��[������^�����n�߂��B�~�ʌ^���[�����܂ޕ��ʓ��ŕ��̂ɓ����͂́A�}3��3��ނł���B���̂��pθ (
�̈ʒu�ŕ��̂ɓ����͂͂荇���A���̂͐Î~���Č�����B���ɁA���̂��荇���̈ʒu���班���������������Ƃ���A���̂̓��[������^�����n�߂��B�~�ʌ^���[�����܂ޕ��ʓ��ŕ��̂ɓ����͂́A�}3��3��ނł���B���̂��pθ (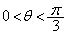 )�̈ʒu�ʼn^�����Ă���Ƃ��A���̂ɓ������[���ɉ����������̗͂̑傫�����A�d�͉����xg��p�����ɕ\���B
)�̈ʒu�ʼn^�����Ă���Ƃ��A���̂ɓ������[���ɉ����������̗͂̑傫�����A�d�͉����xg��p�����ɕ\���B (e) ��(d)�ɂ����āA�p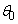 ����̕ψ�
����̕ψ�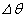 (
(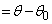 )���\���ɏ������ꍇ�ɂ��čl����B���̂Ƃ��A���̂ɓ������[���ɉ����������̗͂́A�荇���̈ʒu����̋����ɔ�Ⴕ�A���̕����͏�ɂ荇���̈ʒu�������Ă��邽�߁A���̂͒P�U��������B���̒P�U���̎������d�͉����xg��p�����ɕ\���B
)���\���ɏ������ꍇ�ɂ��čl����B���̂Ƃ��A���̂ɓ������[���ɉ����������̗͂́A�荇���̈ʒu����̋����ɔ�Ⴕ�A���̕����͏�ɂ荇���̈ʒu�������Ă��邽�߁A���̂͒P�U��������B���̒P�U���̎������d�͉����xg��p�����ɕ\���B �������A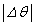 ���\���������Ƃ��A
���\���������Ƃ��A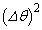 �̍��͖������邱�Ƃ��ł��A�K�v�Ȃ玟�̎���p����B
�̍��͖������邱�Ƃ��ł��A�K�v�Ȃ玟�̎���p����B 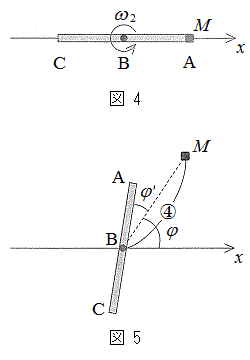 (f) ��(c)�̏�Ԃ���A���[���̊p���xω ���������Ƒ����������B���̉ߒ��ɂ����Ċp���x�̕ω��͏\�����������߁A�Z�����Ԃɂ����镨�̂̉^���͊p���xω �̓����~�^�����݂Ȃ����Ƃ��ł���B�p���x��
(f) ��(c)�̏�Ԃ���A���[���̊p���xω ���������Ƒ����������B���̉ߒ��ɂ����Ċp���x�̕ω��͏\�����������߁A�Z�����Ԃɂ����镨�̂̉^���͊p���xω �̓����~�^�����݂Ȃ����Ƃ��ł���B�p���x��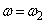 �ɒB�����Ƃ��A���̂̓��[���̒[A���痣�ꂽ�B���̂Ƃ��A���[����^�ォ�猩��ƁA���ʂŒ�`����Ă���x���ƁA�}4�̂悤�ɏd�Ȃ��Č������B���̌�A���[�����痣�ꂽ���̂͂��炭���ď��ɗ������A���[���͊p���x
�ɒB�����Ƃ��A���̂̓��[���̒[A���痣�ꂽ�B���̂Ƃ��A���[����^�ォ�猩��ƁA���ʂŒ�`����Ă���x���ƁA�}4�̂悤�ɏd�Ȃ��Č������B���̌�A���[�����痣�ꂽ���̂͂��炭���ď��ɗ������A���[���͊p���x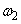 ��ۂ����܂܉�]�����B���̂����������Ƃ��A���̂ƃ��[����^�ォ�猩��ƁA�}5�̂悤�Ɍ������B
��ۂ����܂܉�]�����B���̂����������Ƃ��A���̂ƃ��[����^�ォ�猩��ƁA�}5�̂悤�Ɍ������B
[2]�@�ʐ�S�̓����`��������̋ɔ�A��B���Ԋud�Ō��������킹�ɔz�u���ꂽ���s�R���f���T�[���A�^�ɒu���B���̃R���f���T�[�̋ɔԂɁA���̋ɔƓ����`������ʐ�S�̋�����P���A�ɔ�A���狗��x���u�Ăċɔɑ��ĕ��s�ɒu���B�^��̗U�d����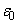 �Ƃ��Ĉȉ��̖₢�ɓ�����B�������A�ɔ[�ʂ���ы����[�ʂɂ�����d��̗���͂Ȃ��A�d�C�͐��͋ɔԂɌ�������̂Ƃ���B�����A�ɔA�����̒�R�A�d�͖͂�������B�܂������̌�������������B
�Ƃ��Ĉȉ��̖₢�ɓ�����B�������A�ɔ[�ʂ���ы����[�ʂɂ�����d��̗���͂Ȃ��A�d�C�͐��͋ɔԂɌ�������̂Ƃ���B�����A�ɔA�����̒�R�A�d�͖͂�������B�܂������̌�������������B
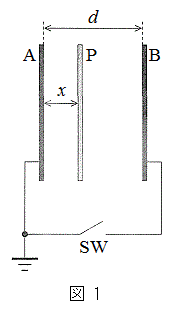 [A]�@�}1�̂悤�ɁA�ɔ�A��B�́A�X�C�b�`SW����Đڑ�����A�ɔ�A�͐ڒn����Ă���B
[A]�@�}1�̂悤�ɁA�ɔ�A��B�́A�X�C�b�`SW����Đڑ�����A�ɔ�A�͐ڒn����Ă���B(a) �X�C�b�`SW���J���Ă���Ƃ��A�ɔ�A�CB�Ԃ̓d�C�e�ʂ����߂�B
(b) �X�C�b�`SW�������A������P��d�C��Q�̐��d�ׂőѓd������B���̓d�ׂɂ���ċɔ�A��B�ɗU�������d�C�ʂ��A���ꂼ�ꋁ�߂�B
(c) ��(b)�ɂ����āA�R���f���T�[�ɒ~�����Ă���Ód�G�l���M�[�����߂�B
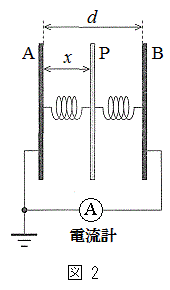 [B]�@���ɁA����m�̋�����P��d�C��Q�̐��d�ׂőѓd�������܂܁A�}2�̂悤�Ɏ��R��
[B]�@���ɁA����m�̋�����P��d�C��Q�̐��d�ׂőѓd�������܂܁A�}2�̂悤�Ɏ��R��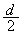 �C�˒萔k��2�̓����≏�̂̂˂ɐڑ�����B�˂̑��[�́A�Œ肳�ꂽ�ɔ�A��B�ɂ��ꂼ��Ȃ���Ă���B���̋����́A�ɔ�A�CB�ƕ��s��ۂ����܂܁A�ɔɐ����ȕ����ɂ̂ݓ������Ƃ��ł���B�ɔ�A��B�́A�d���v����Đڑ�����A�ɔ�A�͐ڒn����Ă���B�˂�ڑ��������Ƃɂ��d�C�e�ʂ̕ω��A�d���v�̒�R�A�����̐U���ɂ��d���g�̔����͖�������B
�C�˒萔k��2�̓����≏�̂̂˂ɐڑ�����B�˂̑��[�́A�Œ肳�ꂽ�ɔ�A��B�ɂ��ꂼ��Ȃ���Ă���B���̋����́A�ɔ�A�CB�ƕ��s��ۂ����܂܁A�ɔɐ����ȕ����ɂ̂ݓ������Ƃ��ł���B�ɔ�A��B�́A�d���v����Đڑ�����A�ɔ�A�͐ڒn����Ă���B�˂�ڑ��������Ƃɂ��d�C�e�ʂ̕ω��A�d���v�̒�R�A�����̐U���ɂ��d���g�̔����͖�������B(e) ������P�̈ʒu��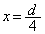 �Ɉړ������Ă�������B���̂Ƃ��A������P���P�U�����邽�߂ɕK�v�ƂȂ�Q�ɋ��߂��������k�C
�Ɉړ������Ă�������B���̂Ƃ��A������P���P�U�����邽�߂ɕK�v�ƂȂ�Q�ɋ��߂��������k�C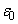 �CS�Cd��p���ĕ\���B�܂��A���̏��������Ƃ��A�P�U���̊p�U���������߂�B
�CS�Cd��p���ĕ\���B�܂��A���̏��������Ƃ��A�P�U���̊p�U���������߂�B [��]
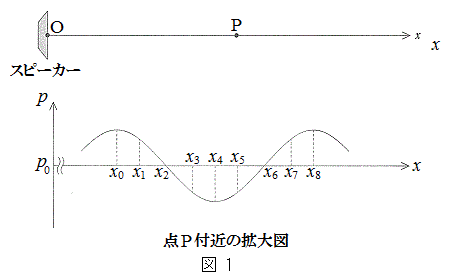 [3][A]�@�}1��}�̂悤�Ɍ��_O�ɃX�s�[�J�[��u���A���̐U���ŁA���̐U����f �̉��g��x ���̐��̌����ɘA���I�ɔ���������B��C�̈��͕ω��ɔ������鏬���ȃ}�C�N���z�����p���āAx����(
[3][A]�@�}1��}�̂悤�Ɍ��_O�ɃX�s�[�J�[��u���A���̐U���ŁA���̐U����f �̉��g��x ���̐��̌����ɘA���I�ɔ���������B��C�̈��͕ω��ɔ������鏬���ȃ}�C�N���z�����p���āAx����(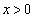 )�̊e�_�ň���p�̎��ԕω��𑪒肷��B
)�̊e�_�ň���p�̎��ԕω��𑪒肷��B
���鎞���ɂ����āAx����(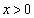 )�̓_P�t�߂̋�C�̈���p��x�̊��Ƃ��Ē��ׂ��Ƃ���A�}1���}�̃O���t�̂悤�ɂȂ����B�����ŋ���OP�͉��g�̔g�������\�������A�܂����g�����݂��Ȃ��Ƃ��̑�C�̈��͂�
)�̓_P�t�߂̋�C�̈���p��x�̊��Ƃ��Ē��ׂ��Ƃ���A�}1���}�̃O���t�̂悤�ɂȂ����B�����ŋ���OP�͉��g�̔g�������\�������A�܂����g�����݂��Ȃ��Ƃ��̑�C�̈��͂�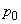 �Ƃ���B����p�͍ő�l���Ƃ�
�Ƃ���B����p�͍ő�l���Ƃ�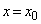 ����A���ɍő�l���Ƃ�
����A���ɍő�l���Ƃ�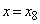 �܂ł�x�̋�Ԃ�8�������A
�܂ł�x�̋�Ԃ�8�������A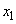 �C
�C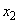 �C����C
�C����C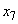 �Ə���x���W���߂�B
�Ə���x���W���߂�B (a) 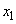 ����
����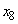 �܂ł̊e�ʒu�̒��ŁAx���̐��̌����ɋ�C���ł��傫���ψʂ��Ă���ʒu�A�����x���̐��̌����ɋ�C���ł����������Ă���ʒu�͂��ꂼ��ǂꂩ�B
�܂ł̊e�ʒu�̒��ŁAx���̐��̌����ɋ�C���ł��傫���ψʂ��Ă���ʒu�A�����x���̐��̌����ɋ�C���ł����������Ă���ʒu�͂��ꂼ��ǂꂩ�B 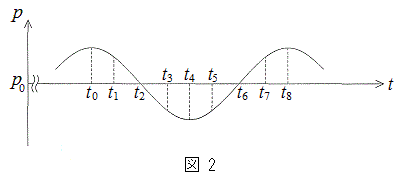 ���ɓ_P�ŋ�C�̈���p�̎��ԕω��ׂ��Ƃ���A�}2�̃O���t�̂悤�ɂȂ����B����p���ő�l���Ƃ鎞��
���ɓ_P�ŋ�C�̈���p�̎��ԕω��ׂ��Ƃ���A�}2�̃O���t�̂悤�ɂȂ����B����p���ő�l���Ƃ鎞��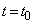 ����A���ɍő�l���Ƃ鎞���܂ł�1������8�������A
����A���ɍő�l���Ƃ鎞���܂ł�1������8�������A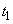 �C
�C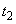 �C����C
�C����C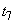 �Ə��Ɏ������߂�B
�Ə��Ɏ������߂�B(b) 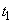 ����
����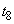 �܂ł̊e�����̒��ŁAx���̐��̌����ɋ�C���ł��傫���ψʂ��Ă���̂͂ǂ̎������B
�܂ł̊e�����̒��ŁAx���̐��̌����ɋ�C���ł��傫���ψʂ��Ă���̂͂ǂ̎������B 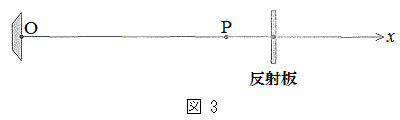 �}3�̂悤�ɁA���_O���猩�ē_P��艓�����̈ʒu�ɁAx���ɑ��Đ����ɔ��˔�u���ƁA���͂����ԂƂƂ��ɕς�炸���
�}3�̂悤�ɁA���_O���猩�ē_P��艓�����̈ʒu�ɁAx���ɑ��Đ����ɔ��˔�u���ƁA���͂����ԂƂƂ��ɕς�炸���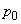 �ƂȂ�_��x����ɓ��Ԋu�ɕ��B
�ƂȂ�_��x����ɓ��Ԋu�ɕ��B(c) �����̗אڂ���_�̊Ԋud�͂����炩�B�Ȃ��A���g�̑�����c�Ƃ���B
(d) ��(c)�̏�Ԃ���C�����㏸�����Ƃ���A��(c)�ŋ��߂�d�͑��������B���̗��R���������B
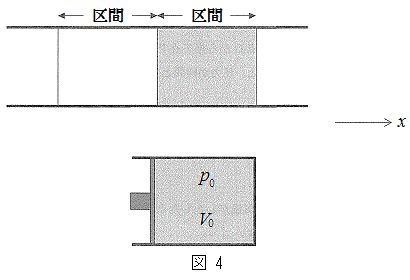 [B]�@���g����C����`���Ƃ��A�e�����ł͋�C�̈��k�Ɩc�����J��Ԃ���Ă���B���k�Ɩc���͔M�̓`�B���͂₭�N���邽�߁A�f�M�ω��Ƃ݂Ȃ����Ƃ��ł���B���g����C�����ǂ̂悤�ɓ`��邩�ɂ��Ď肪����邽�߁A��C�𗝑z�C�̂Ƃ��Ĉȉ��̂悤�ȊȒP�ȃ��f�����l����B
[B]�@���g����C����`���Ƃ��A�e�����ł͋�C�̈��k�Ɩc�����J��Ԃ���Ă���B���k�Ɩc���͔M�̓`�B���͂₭�N���邽�߁A�f�M�ω��Ƃ݂Ȃ����Ƃ��ł���B���g����C�����ǂ̂悤�ɓ`��邩�ɂ��Ď肪����邽�߁A��C�𗝑z�C�̂Ƃ��Ĉȉ��̂悤�ȊȒP�ȃ��f�����l����B�}4��}�̂悤�ɋ�C��x�������ɍׂ������Ԋu�ɕ������A�e��Ԃ��s�X�g���t���̉~���f�M�e��ɕ����߂�ꂽ��C�Œu��������B�}4���}�͂��̂ЂƂ̕��������������̂ł���B�����Ńs�X�g���͂Ȃ߂炩�ɓ������Ƃ��ł��A�܂���C��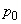 �ɂ�����e����̋�C�̑̐ς�
�ɂ�����e����̋�C�̑̐ς�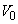 �Ƃ���B
�Ƃ���B
���g�����B���邱�Ƃɂ��s�X�g���͗אڂ����C����͂��A�e����̋�C�̈��͂�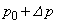 �ɑ�����(
�ɑ�����(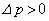 )�C�̐ς�
)�C�̐ς�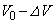 �Ɍ���(
�Ɍ���(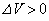 )�����Ƃ��悤�B�������A
)�����Ƃ��悤�B�������A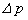 ��
��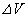 �́A���ꂼ��
�́A���ꂼ��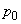 ��
��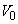 �ɔ�\���������ʂƂ���B�ȉ��̌v�Z�ł́A�����ʂǂ����̐�
�ɔ�\���������ʂƂ���B�ȉ��̌v�Z�ł́A�����ʂǂ����̐�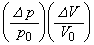 �͖������Ă悢�B�܂��K�v�Ȃ�A������h (
�͖������Ă悢�B�܂��K�v�Ȃ�A������h (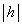 ��1�ɔ�ׂď\��������)�A�[���łȂ���n�ɑ��Đ��藧�ߎ���
��1�ɔ�ׂď\��������)�A�[���łȂ���n�ɑ��Đ��藧�ߎ���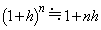 ��p����B
��p����B (e) �e����ɕ����߂�ꂽ��C�̈��͂̑�����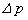 �Ƒ̐ς̌�����
�Ƒ̐ς̌�����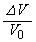 �̔��
�̔��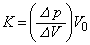 �Ƃ����B�f�M�ω��̂��Ƃł́A����p�Ƒ̐�V�̊Ԃ�
�Ƃ����B�f�M�ω��̂��Ƃł́A����p�Ƒ̐�V�̊Ԃ�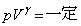 �̊W�����藧���Ƃ�p����K�����߂�B������γ �́A�舳������M���σ�����M�Ŋ������萔�ł���B
�̊W�����藧���Ƃ�p����K�����߂�B������γ �́A�舳������M���σ�����M�Ŋ������萔�ł���B (f) ��C����`��鉹�g�̑���c�́AK�Ƌ�C�̖��xρ �Ƃ�p����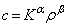 �ƕ\���邱�Ƃ��킩���Ă���B���ӂ̎������ׂ邱�Ƃɂ��Aα��β�̒l�����߂�B
�ƕ\���邱�Ƃ��킩���Ă���B���ӂ̎������ׂ邱�Ƃɂ��Aα��β�̒l�����߂�B [��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B