�����H�Ƒ�w2020�N�O�������������
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
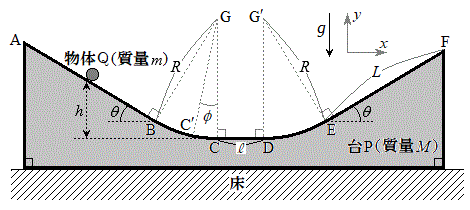 [1]�@�}�̂悤�ɁA2�̎Ζ�AB(���ɑ���X�Ίpθ)�CEF(����L�C���ɑ���X�Ίpθ)�Ɛ����Ȗ�CD(����
[1]�@�}�̂悤�ɁA2�̎Ζ�AB(���ɑ���X�Ίpθ)�CEF(����L�C���ɑ���X�Ίpθ)�Ɛ����Ȗ�CD(����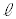 )���A2�̉~�ʖ�BC(���S�_G�C���aR)�CDE(���S�_
)���A2�̉~�ʖ�BC(���S�_G�C���aR)�CDE(���S�_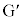 �C���aR)�łȂ߂炩�ɂȂ�����P (����M)�������ȏ��̏�ɒu����Ă���B���̑�P��ɒu���ꂽ�傫���̖����ł��镨��Q (����m)���A�ʂɉ����Ė��C�Ȃ��ɉ^������B�������A�Ζ�AB�̒�����L��蒷���A����Q�͑�P�̒[�_F�ɒB�����Ƃ��ɂ́A��P���痣��邱�Ƃ��ł���Ƃ���B�܂��A��P�C����Q�͂�������}�̉��s�������ɂ͈ړ����Ȃ����̂Ƃ���B����������x�����A����������y�����Ƃ�A���ꂼ��}�̉E�����A������𐳂Ƃ���B��C��R�͖����ł���Ƃ��A�d�͉����x�̑傫����
�C���aR)�łȂ߂炩�ɂȂ�����P (����M)�������ȏ��̏�ɒu����Ă���B���̑�P��ɒu���ꂽ�傫���̖����ł��镨��Q (����m)���A�ʂɉ����Ė��C�Ȃ��ɉ^������B�������A�Ζ�AB�̒�����L��蒷���A����Q�͑�P�̒[�_F�ɒB�����Ƃ��ɂ́A��P���痣��邱�Ƃ��ł���Ƃ���B�܂��A��P�C����Q�͂�������}�̉��s�������ɂ͈ړ����Ȃ����̂Ƃ���B����������x�����A����������y�����Ƃ�A���ꂼ��}�̉E�����A������𐳂Ƃ���B��C��R�͖����ł���Ƃ��A�d�͉����x�̑傫����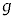 �Ƃ��āA�ȉ��̖�ɓ�����B
�Ƃ��āA�ȉ��̖�ɓ�����B
[A]�@��P�����ɌŒ肳��Ă���ꍇ���l����B
(a) �Ζ�AB��Ŗ�CD�ɑ��č���h�̏ꏊ�ɕ���Q��u���ď����x�Ȃ��ɕ������B����Q�����߂ē_D�ɒB�����Ƃ��̕���Q�̏��ɑ��鑬�x��x���������߂�B
(b) ��(a)�ɂ����āAh������l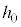 ���傫���Ƃ��A����Q�͒[�_F�ɒB���đ�P���痣��邪�Ah��
���傫���Ƃ��A����Q�͒[�_F�ɒB���đ�P���痣��邪�Ah��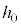 ��菬�����Ƃ��A����Q�͑�P���痣��Ȃ��B���̂悤��
��菬�����Ƃ��A����Q�͑�P���痣��Ȃ��B���̂悤��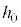 ��m�CM�C
��m�CM�C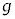 �C
�C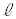 �CR�Cθ�̂����K�v�Ȃ��̂�p���ĕ\���B
�CR�Cθ�̂����K�v�Ȃ��̂�p���ĕ\���B
(c) ��(a)�ɂ����āAh��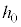 ���傫���Ƃ��A����Q�͒[�_F�ɒB������A��P���痣���B����Q���[�_F�𗣂�Ă���ō��_�ɒB����܂ł̎��Ԃ��Am�CM�C
���傫���Ƃ��A����Q�͒[�_F�ɒB������A��P���痣���B����Q���[�_F�𗣂�Ă���ō��_�ɒB����܂ł̎��Ԃ��Am�CM�C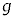 �Ch�C
�Ch�C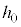 �Cθ�̂����K�v�Ȃ��̂�p���ĕ\���B
�Cθ�̂����K�v�Ȃ��̂�p���ĕ\���B
(d) �~�ʖ�BC��̓_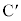 �ɕ���Q��u���ď����x�Ȃ��ɕ������Ƃ���A����Q�͖�CD����ړ����A�~�ʖ�DE��̓_�ɒB������A�������犊��~��čĂѓ_
�ɕ���Q��u���ď����x�Ȃ��ɕ������Ƃ���A����Q�͖�CD����ړ����A�~�ʖ�DE��̓_�ɒB������A�������犊��~��čĂѓ_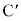 �ɖ߂�����^�����s�����B���̉^���̎����ɂ��ďq�ׂ����̕��͂ɂ����āA��(�A)�`(�G)�ɓ��Ă͂܂鐔������B�������A����
�ɖ߂�����^�����s�����B���̉^���̎����ɂ��ďq�ׂ����̕��͂ɂ����āA��(�A)�`(�G)�ɓ��Ă͂܂鐔������B�������A���� ������CG�ƂȂ��p
������CG�ƂȂ��p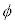 �͏\���ɏ������A����Q�̉~�ʖʏ�̉^���͒P�U���ƌ��Ȃ�����̂Ƃ��A�K�v�Ȃ�
�͏\���ɏ������A����Q�̉~�ʖʏ�̉^���͒P�U���ƌ��Ȃ�����̂Ƃ��A�K�v�Ȃ�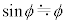 �C
�C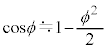 �̋ߎ�����p���Ă悢�B
�̋ߎ�����p���Ă悢�B
����Q���_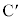 ���珉�߂ē_C�ɒB����܂ł̎��Ԃ�
���珉�߂ē_C�ɒB����܂ł̎��Ԃ� �ł���B�܂��A�_C�ɒB�����Ƃ��̕���Q�̑�����
�ł���B�܂��A�_C�ɒB�����Ƃ��̕���Q�̑�����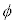 �ɔ�Ⴕ����
�ɔ�Ⴕ���� �ŕ\�����Ƃ��ł���B���̂��Ƃ���A����Q���_C���珉�߂ē_D�ɒB����܂ł̎��Ԃ�
�ŕ\�����Ƃ��ł���B���̂��Ƃ���A����Q���_C���珉�߂ē_D�ɒB����܂ł̎��Ԃ� �ƕ\����B���������āA���̉^���̎�����
�ƕ\����B���������āA���̉^���̎����� �ł���B
�ł���B
[B]�@��P�������痣��邱�ƂȂ����C�Ȃ���x�����Ɉړ��ł���ꍇ���l����B
(e) ��P�����ɑ��ĐÎ~���Ă���Ƃ��A�Ζ�AB��Ŗ�CD�ɑ��č���h�̏ꏊ�ɕ���Q��u���ď����x�Ȃ��ɕ������B����Q�����߂ē_D�ɒB�����Ƃ��̕���Q����ё�P�̏��ɑ��鑬�x��x����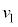 �C
�C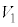 �����ꂼ�ꋁ�߂�B
�����ꂼ�ꋁ�߂�B
(f) ��(e)�ɂ����āAh������l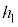 ���傫���Ƃ��A����Q�͒[�_F�ɒB���đ�P���痣��邪�Ah��
���傫���Ƃ��A����Q�͒[�_F�ɒB���đ�P���痣��邪�Ah��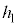 ��菬�����Ƃ��A����Q�͑�P���痣��Ȃ��B���̂悤��
��菬�����Ƃ��A����Q�͑�P���痣��Ȃ��B���̂悤��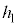 ��m�CM�C
��m�CM�C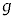 �C
�C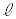 �CR�Cθ�̂����K�v�Ȃ��̂�p���ĕ\���B
�CR�Cθ�̂����K�v�Ȃ��̂�p���ĕ\���B
(g) ��(e)�ɂ����āAh��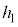 ���傫���Ƃ��A����Q�͒[�_F�ɒB������A��P���痣���B���̏u�Ԃ̑�P�̏��ɑ��鑬�x��x����
���傫���Ƃ��A����Q�͒[�_F�ɒB������A��P���痣���B���̏u�Ԃ̑�P�̏��ɑ��鑬�x��x����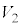 �ɂ��ďq�ׂ����̕��͂ɂ����āA��(�I)�C(�J)�ɓ��Ă͂܂鐔������A
�ɂ��ďq�ׂ����̕��͂ɂ����āA��(�I)�C(�J)�ɓ��Ă͂܂鐔������A ����Q����P���痣���u�Ԃɂ����镨��Q�̏��ɑ��鑬�x��x���������y���������ꂼ��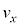 �C
�C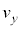 �Ƃ���ƁA����Q���Ζ�EF����^�����Ă������Ƃ���A
�Ƃ���ƁA����Q���Ζ�EF����^�����Ă������Ƃ���A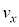 �C
�C �C
�C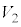 �̊Ԃɂ͎Ζ�EF�̌X�Ίpθ�Ō��܂�W��
�̊Ԃɂ͎Ζ�EF�̌X�Ίpθ�Ō��܂�W�� �����藧�B���̎��ƁA�͊w�I�G�l���M�[�ۑ�������щ^���ʕۑ�����A�����ĉ����ƁA
�����藧�B���̎��ƁA�͊w�I�G�l���M�[�ۑ�������щ^���ʕۑ�����A�����ĉ����ƁA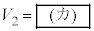 �ƕ\�����B
�ƕ\�����B
[C]�@����Q�̒u���ꂽ��P�����x�����ɉ����xa (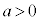 )�̓������x�^�����s���悤�ɁA��P�ɓK�ȊO��T��������ꍇ���l����B��P�́A�����痣��邱�ƂȂ����C�Ȃ���x���̐��̌����ɉ^��������̂Ƃ���B
)�̓������x�^�����s���悤�ɁA��P�ɓK�ȊO��T��������ꍇ���l����B��P�́A�����痣��邱�ƂȂ����C�Ȃ���x���̐��̌����ɉ^��������̂Ƃ���B
(h) �~�ʖ�BC��ɂ��镨��Q���A�_B�CC���邱�ƂȂ���P���猩�ĒP�U���ƌ��Ȃ���\���ɐU���̏����Ȏ����^�����s�����B���̉^���̎��������߂�B
(i) ���ɁA�Ζ�AB��ɕ���Q���u���ꂽ���l����B��P�����ɑ��ċ���s�����ړ������Ă���ԁA����Q�͎Ζ�AB��ʼn^�����Ă����B���̊ԂɊO��T���s�����d���̑傫����m�CM�C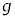 �Cs�Cθ�Ca��p���ĕ\���B
�Cs�Cθ�Ca��p���ĕ\���B [��]
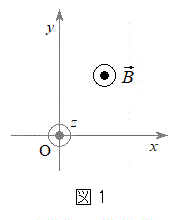 [2]�@�d���ꒆ�ɂ����鎿��m�C�d��q�̉דd���q�̉^�����l�@����B�f��̂Ȃ�����Aq�͐���������̒l����肤����̂Ƃ���B�������x
[2]�@�d���ꒆ�ɂ����鎿��m�C�d��q�̉דd���q�̉^�����l�@����B�f��̂Ȃ�����Aq�͐���������̒l����肤����̂Ƃ���B�������x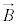 �́A���ԓI�ɕω����邱�Ƃ͂Ȃ��Ƃ���B�܂��A�������x
�́A���ԓI�ɕω����邱�Ƃ͂Ȃ��Ƃ���B�܂��A�������x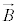 �̌����́A�}1�̂悤�Ɏ��ʂ̗�����\�̌����ł���A���̌�����z���̐��̌����Ƃ��A�דd���q��xy���ʓ����^��������̂Ƃ���B�Ȃ��A�דd���q�͐^���^��������̂Ƃ��A�܂��A�d�͂̉e���͖����ł�����̂Ƃ���B
�̌����́A�}1�̂悤�Ɏ��ʂ̗�����\�̌����ł���A���̌�����z���̐��̌����Ƃ��A�דd���q��xy���ʓ����^��������̂Ƃ���B�Ȃ��A�דd���q�͐^���^��������̂Ƃ��A�܂��A�d�͂̉e���͖����ł�����̂Ƃ���B
[A]�@�������x�̑傫��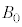 �̈�l�Ȏ��ꒆ�ŁA�דd���q������
�̈�l�Ȏ��ꒆ�ŁA�דd���q������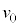 ��xy���ʏ�̓����~�^�����s���Ă���Ƃ���B�Ȃ��A�ݖ�[A]�ł́A�d��͂������Ă��Ȃ����̂Ƃ���B�ȉ��̖�ɓ�����B
��xy���ʏ�̓����~�^�����s���Ă���Ƃ���B�Ȃ��A�ݖ�[A]�ł́A�d��͂������Ă��Ȃ����̂Ƃ���B�ȉ��̖�ɓ�����B
(a) �~�^���̔��a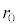 ���Am�C
���Am�C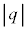 �C
�C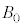 �C
�C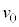 �̂����K�v�Ȃ��̂�p���ĕ\���B
�̂����K�v�Ȃ��̂�p���ĕ\���B
(b) �דd���q�̑��x��x�Cy���������ꂼ��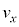 �C
�C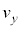 �Ƃ��A�דd���q����͂�x�Cy���������ꂼ��
�Ƃ��A�דd���q����͂�x�Cy���������ꂼ��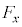 �C
�C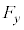 �Ƃ���B
�Ƃ���B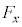 �����
�����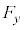 ���Aq�C
���Aq�C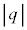 �C
�C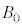 �C
�C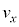 �C
�C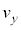 �̂����K�v�Ȃ��̂�p���Ă��ꂼ��\���B
�̂����K�v�Ȃ��̂�p���Ă��ꂼ��\���B
[B]�@���ɁA�������x�̌�����z���̐��̌����̂܂܁A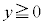 �ł͎������x�̑傫����
�ł͎������x�̑傫����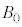 �C
�C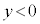 �ł͎������x�̑傫����
�ł͎������x�̑傫����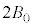 �ł���Ƃ���B�Ȃ��A�ݖ�[B]�ł��A�d��͂������Ă��Ȃ����̂Ƃ���B
�ł���Ƃ���B�Ȃ��A�ݖ�[B]�ł��A�d��͂������Ă��Ȃ����̂Ƃ���B ����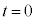 �ɂ����āA�דd���q�����_O��y���̐��̌����ɑ���
�ɂ����āA�דd���q�����_O��y���̐��̌����ɑ���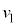 �Œʉ߂����Bn�𐳂̐����Ƃ��āA�דd���q��
�Œʉ߂����Bn�𐳂̐����Ƃ��āA�דd���q��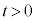 ��n��ڂ�x�������鎞��(���Ȃ킿y���W���[���ƂȂ鎞��)��
��n��ڂ�x�������鎞��(���Ȃ킿y���W���[���ƂȂ鎞��)��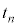 �C���̂Ƃ���x���W��
�C���̂Ƃ���x���W��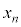 �Ə������Ƃɂ���B�ȉ��̖�ɓ�����B
�Ə������Ƃɂ���B�ȉ��̖�ɓ�����B
(c) m�Cq�C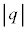 �C
�C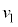 �C
�C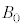 �̂����K�v�Ȃ��̂�p���āA
�̂����K�v�Ȃ��̂�p���āA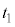 �C
�C �C
�C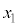 �����
�����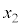 ��\���B
��\���B
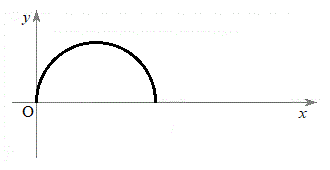 (d) �דd���q��y���W�̂Ƃ肤��ő�l����эŏ��l���Am�C
(d) �דd���q��y���W�̂Ƃ肤��ő�l����эŏ��l���Am�C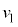 �Cq�C
�Cq�C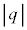 �C
�C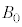 �̂����K�v�Ȃ��̂�p���ĕ\���B����ɁA���̃O���t�ɁA
�̂����K�v�Ȃ��̂�p���ĕ\���B����ɁA���̃O���t�ɁA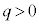 �̏ꍇ��
�̏ꍇ��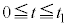 �̊Ԃ̉דd���q�̋O��(���~)���L����Ă���B����ɂЂ��Â��A
�̊Ԃ̉דd���q�̋O��(���~)���L����Ă���B����ɂЂ��Â��A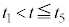 �̊Ԃ̉דd���q�̋O�Ղ̊T�`�����̃O���t�ɕ`��������B
�̊Ԃ̉דd���q�̋O�Ղ̊T�`�����̃O���t�ɕ`��������B
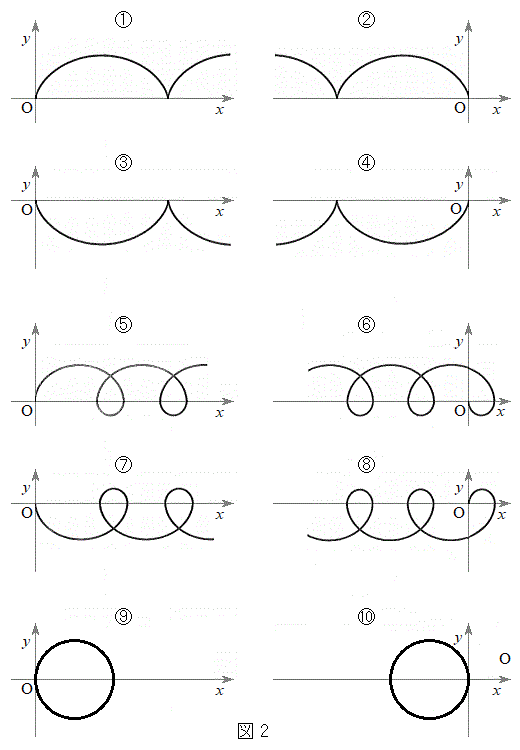 [C]�@���ɁAz���̐��̌����̎���ɉ����āA�d�������ꍇ���l����B�ݖ�[C]�ł́A�������x�͈�l�ő傫��
[C]�@���ɁAz���̐��̌����̎���ɉ����āA�d�������ꍇ���l����B�ݖ�[C]�ł́A�������x�͈�l�ő傫��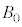 �Ƃ���B�����A�d���y���̐��̌����������Ă���A��l�ő傫��
�Ƃ���B�����A�d���y���̐��̌����������Ă���A��l�ő傫��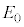 �Ƃ���B����
�Ƃ���B����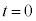 �ɂ����āA�דd���q�͌��_O�ɐÎ~���Ă���Ƃ���B�����ŁA����t�ɂ�����דd���q�̑��x��x�Cy�������A���ꂼ��
�ɂ����āA�דd���q�͌��_O�ɐÎ~���Ă���Ƃ���B�����ŁA����t�ɂ�����דd���q�̑��x��x�Cy�������A���ꂼ��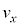 �C
�C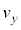 �ƕ\�����ƂƂ���B�ȉ��̖�ɓ�����B
�ƕ\�����ƂƂ���B�ȉ��̖�ɓ�����B
(e) ����t�ɂ����āA�דd���q����͂�x�Cy���������ꂼ��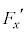 �C
�C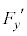 �Ƃ���B
�Ƃ���B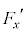 �����
�����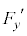 ���Aq�C
���Aq�C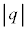 �C
�C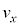 �C
�C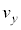 �C
�C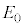 �C
�C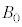 �̂����K�v�Ȃ��̂�p���Ă��ꂼ��\���B
�̂����K�v�Ȃ��̂�p���Ă��ꂼ��\���B
(f) ���鑬��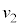 ��x���̐��̌����ɓ����x�^������ϑ��҂��猩���ꍇ�ɂ́A�דd���q�̉^���������~�^���Ɍ�����B m�Cq�C
��x���̐��̌����ɓ����x�^������ϑ��҂��猩���ꍇ�ɂ́A�דd���q�̉^���������~�^���Ɍ�����B m�Cq�C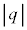 �C
�C �����
�����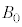 �̂����K�v�Ȃ��̂�p����
�̂����K�v�Ȃ��̂�p����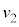 ��\���B
��\���B
(g) 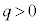 �̏ꍇ��
�̏ꍇ��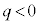 �̏ꍇ�̂��ꂼ��ɂ��A����
�̏ꍇ�̂��ꂼ��ɂ��A����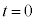 ���炵�炭�̊Ԃ́A�Î~�����ϑ��҂��猩���דd���q�̋O�Ղ̊T�`�Ƃ��āA�����Ƃ��ӂ��킵�����̂��A�}2�̑I�����@�`�I���炻�ꂼ��1���I�ׁB
���炵�炭�̊Ԃ́A�Î~�����ϑ��҂��猩���דd���q�̋O�Ղ̊T�`�Ƃ��āA�����Ƃ��ӂ��킵�����̂��A�}2�̑I�����@�`�I���炻�ꂼ��1���I�ׁB
(h) 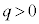 �̏ꍇ���l����B�דd���q��y���W�̂Ƃ肤��ő�l
�̏ꍇ���l����B�דd���q��y���W�̂Ƃ肤��ő�l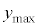 �́A(f)�ŋ��߂�
�́A(f)�ŋ��߂�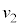 ��p���ĉ��L�̂悤�ɂȂ�B��
��p���ĉ��L�̂悤�ɂȂ�B�� �ɓ��Ă͂܂鐔����m�Cq�C
�ɓ��Ă͂܂鐔����m�Cq�C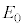 �C
�C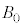 �̂����K�v�Ȃ��̂�p���ĕ\���B
�̂����K�v�Ȃ��̂�p���ĕ\���B
�܂��A�Î~�����ϑ��҂��猩���ꍇ�ɁA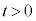 �ɂ����čŏ���
�ɂ����čŏ���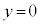 �ƂȂ�Ƃ���x���W�̐�Βl
�ƂȂ�Ƃ���x���W�̐�Βl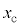 �́A���L�̂悤��
�́A���L�̂悤��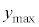 �̒萔�{�ƂȂ��Ă���B��
�̒萔�{�ƂȂ��Ă���B�� �߂�B
�߂�B
 (i) ��������
(i) ��������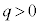 �̏ꍇ���l����B�Î~�����ϑ��҂��猩���ꍇ�ɁA����
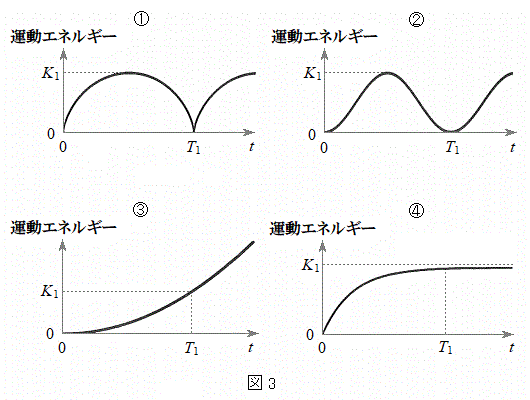
�̏ꍇ���l����B�Î~�����ϑ��҂��猩���ꍇ�ɁA����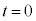 ���炵�炭�̊Ԃ̉דd���q�̉^���G�l���M�[�̕ω��̗l�q�Ƃ��Ă����Ƃ��ӂ��킵�����̂��A�}3�̑I�����@�`�C����I�ׁB�������A�}3�̉����ɂ���
���炵�炭�̊Ԃ̉דd���q�̉^���G�l���M�[�̕ω��̗l�q�Ƃ��Ă����Ƃ��ӂ��킵�����̂��A�}3�̑I�����@�`�C����I�ׁB�������A�}3�̉����ɂ���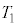 �́A�דd���q��y���W��
�́A�דd���q��y���W��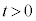 �ōŏ��Ƀ[���ƂȂ鎞����\���B
�ōŏ��Ƀ[���ƂȂ鎞����\���B
[��]
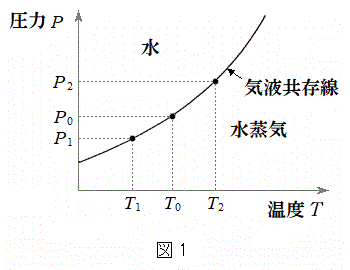 [3]�@�t�̏�Ԃ̐�(�ȉ��ł͒P�ɐ��ƌĂ�)���V�����_�[�ɖ������Ĉ��͈��̂��Ƃʼn��M���Ă����ƁA���̉��x���㏸���A���鉷�x�ɒB����Ɛ����琅���C�ւ̕ω�(����)��������B���̉��x���C�t�������x(���_)�ƌĂсA���̉��x�ɂ����Ă͐��Ɛ����C�������ł���B�C�t�������x�ɂ����Ĉ��ʂ̐������ׂĐ����C�ɕω�������̂ɕK�v�ȔM�ʂ������M�ƌĂԁB���̋C�t�������x�ƈ��͂̊W���}1���ɋC�t�������Ƃ��Ď�����Ă���B�}1�̏c���͈��́A�����͉��x�ł���A�C�t�������̍����̗̈�ł͐��A�E���̗̈�ł͐����C�ƂȂ�A�C�t�������x�͈��͂̑����ƂƂ��ɏ㏸����B
[3]�@�t�̏�Ԃ̐�(�ȉ��ł͒P�ɐ��ƌĂ�)���V�����_�[�ɖ������Ĉ��͈��̂��Ƃʼn��M���Ă����ƁA���̉��x���㏸���A���鉷�x�ɒB����Ɛ����琅���C�ւ̕ω�(����)��������B���̉��x���C�t�������x(���_)�ƌĂсA���̉��x�ɂ����Ă͐��Ɛ����C�������ł���B�C�t�������x�ɂ����Ĉ��ʂ̐������ׂĐ����C�ɕω�������̂ɕK�v�ȔM�ʂ������M�ƌĂԁB���̋C�t�������x�ƈ��͂̊W���}1���ɋC�t�������Ƃ��Ď�����Ă���B�}1�̏c���͈��́A�����͉��x�ł���A�C�t�������̍����̗̈�ł͐��A�E���̗̈�ł͐����C�ƂȂ�A�C�t�������x�͈��͂̑����ƂƂ��ɏ㏸����B
�ȉ��A�{��ł́A����1mol������̑̐�(���Ȃ킿�����̐�)��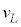 �Ƃ��A
�Ƃ��A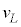 �͉��x�ƈ��͂ɂ�炸���Ƃ݂Ȃ�����̂Ƃ���B
�͉��x�ƈ��͂ɂ�炸���Ƃ݂Ȃ�����̂Ƃ���B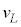 �����Ƃ����̂Œ�σ�����M�ƒ舳������M�͓��������ߗ��҂���ʂ����A���̃�����M��
�����Ƃ����̂Œ�σ�����M�ƒ舳������M�͓��������ߗ��҂���ʂ����A���̃�����M�� �Ƃ���B����1mol������̏����M��L�Ƃ��A�ȉ��ōl���鉷�x�͈͂ł́AL�����
�Ƃ���B����1mol������̏����M��L�Ƃ��A�ȉ��ōl���鉷�x�͈͂ł́AL�����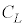 �͉��x�ƈ��͂ɂ�炸���Ƃ݂Ȃ�����̂Ƃ���B����
�͉��x�ƈ��͂ɂ�炸���Ƃ݂Ȃ�����̂Ƃ���B���� �C
�C �C
�C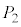 �ɂ�����C�t�������x�����ꂼ��
�ɂ�����C�t�������x�����ꂼ��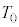 �C
�C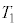 �C
�C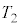 (��Ή��x)�A�C�t������Ԃł̐����C�̃����̐ς����ꂼ��
(��Ή��x)�A�C�t������Ԃł̐����C�̃����̐ς����ꂼ�� �C
�C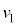 �C
�C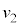 �Ƃ���B�܂��A�s�X�g���̎��ʂ͖����ł���B�s�X�g���ƃV�����_�[�͏\���ɒf�M����Ă���A�V�����_�[�����ɐݒu���ꂽ���M���u�����������M�������A���͂ƃV�����_�[�����Ƃ̊ԂŔM�̎���͂Ȃ����̂Ƃ���B����ɁA�s�X�g���A�V�����_�[�A���M���u�ȂǁA���Ɛ����C�ȊO�̕��̂̔M�e�ʂ͖����ł�����̂Ƃ���B
�Ƃ���B�܂��A�s�X�g���̎��ʂ͖����ł���B�s�X�g���ƃV�����_�[�͏\���ɒf�M����Ă���A�V�����_�[�����ɐݒu���ꂽ���M���u�����������M�������A���͂ƃV�����_�[�����Ƃ̊ԂŔM�̎���͂Ȃ����̂Ƃ���B����ɁA�s�X�g���A�V�����_�[�A���M���u�ȂǁA���Ɛ����C�ȊO�̕��̂̔M�e�ʂ͖����ł�����̂Ƃ���B
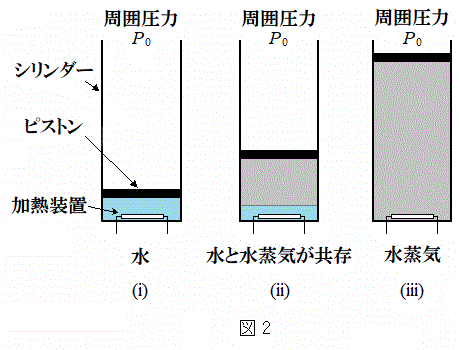 [A]�@�}2(i)�̂悤�Ɋ��炩�ɓ����s�X�g�������V�����_�[�����ɐ�1mol����������Ă���A���͂�
[A]�@�}2(i)�̂悤�Ɋ��炩�ɓ����s�X�g�������V�����_�[�����ɐ�1mol����������Ă���A���͂�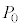 �ň��ɕۂ��Ȃ���A���̃V�����_�[�����̉��M���u�ł��������M���A�M��
�ň��ɕۂ��Ȃ���A���̃V�����_�[�����̉��M���u�ł��������M���A�M��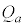 ���������B
���������B
(a) (i)�̏�Ԃ̐��̉��x��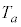 (������
(������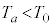 )�ł������B���̕��͒��̋�(�A)�`(�E)�ɓ��Ă͂܂鐔������B
)�ł������B���̕��͒��̋�(�A)�`(�E)�ɓ��Ă͂܂鐔������B 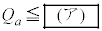 �̏ꍇ�́A�V�����_�[���ɂ͐��݂̂����݂���B
�̏ꍇ�́A�V�����_�[���ɂ͐��݂̂����݂���B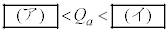 �̏ꍇ�̓V�����_�[���ɂ͐}2(ii)�̂悤�ɐ��Ɛ����C���������A���̂Ƃ��̐����C�̕�����(������)��
�̏ꍇ�̓V�����_�[���ɂ͐}2(ii)�̂悤�ɐ��Ɛ����C���������A���̂Ƃ��̐����C�̕�����(������)�� �ƂȂ�B
�ƂȂ�B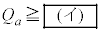 �̏ꍇ�́A�}2(iii)�̂悤�ɃV�����_�[���͐����C�݂̂ƂȂ�B
�̏ꍇ�́A�}2(iii)�̂悤�ɃV�����_�[���͐����C�݂̂ƂȂ�B
(b) ���ɁA����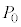 �C���x
�C���x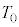 �̐����C1mol������̓����G�l���M�[
�̐����C1mol������̓����G�l���M�[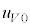 �Ɛ�1mol������̓����G�l���M�[
�Ɛ�1mol������̓����G�l���M�[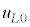 �Ƃ̍��ɂ��čl����B�}2�Ŏ������s�X�g���ƃV�����_�[��p���Ĉ���
�Ƃ̍��ɂ��čl����B�}2�Ŏ������s�X�g���ƃV�����_�[��p���Ĉ���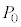 �C���x
�C���x �̐�1mol�����͂Ɖ��x�����̂��ƂŊ��S�ɐ����C�ɕω�������Ƃ��A�s�X�g�����O���ɑ��Ă���d����
�̐�1mol�����͂Ɖ��x�����̂��ƂŊ��S�ɐ����C�ɕω�������Ƃ��A�s�X�g�����O���ɑ��Ă���d����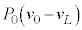 �ŗ^������B���̎��ɉ�����M�ʂ�L�ł��邱�ƁA����єM�͊w�̑�1�@���͋C�̂ɑ��Ă݂̂Ȃ炸�A�t�̂�t�́E�C�̊Ԃ̏�ԕω��ɂ����Ă����藧���Ƃ��l�����āA�����C�Ɛ���1mol������̓����G�l���M�[�̍�
�ŗ^������B���̎��ɉ�����M�ʂ�L�ł��邱�ƁA����єM�͊w�̑�1�@���͋C�̂ɑ��Ă݂̂Ȃ炸�A�t�̂�t�́E�C�̊Ԃ̏�ԕω��ɂ����Ă����藧���Ƃ��l�����āA�����C�Ɛ���1mol������̓����G�l���M�[�̍�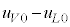 �����߂�B
�����߂�B
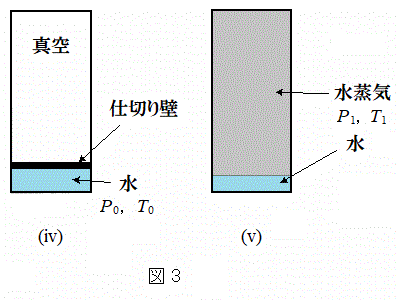 [B] �}3(iv)�Ɏ����悤�Ɏd��ǂ̂��閧�e�킪����A�d��ǂ̉����͈���
[B] �}3(iv)�Ɏ����悤�Ɏd��ǂ̂��閧�e�킪����A�d��ǂ̉����͈���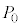 �C���x
�C���x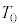 �̐�1mol�Ŗ�������Ă���A�d��ǂ̏㑤�͐^��ɂȂ��Ă���B���̎d��ǂ���菜�����Ƃ���A���̈ꕔ���������A�[�����Ԃ��o�߂�����A�}3(v)�̂悤�ɗe��������͂Ɖ��x�̈�l�ȋC�t������ԂƂȂ����B���̈��͂Ɖ��x�͂������(iv)�̏�Ԃ��Ⴂ
�̐�1mol�Ŗ�������Ă���A�d��ǂ̏㑤�͐^��ɂȂ��Ă���B���̎d��ǂ���菜�����Ƃ���A���̈ꕔ���������A�[�����Ԃ��o�߂�����A�}3(v)�̂悤�ɗe��������͂Ɖ��x�̈�l�ȋC�t������ԂƂȂ����B���̈��͂Ɖ��x�͂������(iv)�̏�Ԃ��Ⴂ �C
�C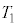 �ł������B�Ȃ��A�e��͊O���ɑ��ď[���ɒf�M����Ă���Ƃ���B
�ł������B�Ȃ��A�e��͊O���ɑ��ď[���ɒf�M����Ă���Ƃ���B
(c) ���̕��͂�(v)�̏�Ԃɂ����鐅���C�̕����ʂ̋��ߕ�������������̂ł���B��(�G)�`(�J)�ɓ��Ă͂܂鐔������B
���̏ꍇ�A�O���Ƃ̊ԂŔM��d���̎��Ȃ��̂ŁA�M�͊w�̑�1�@�����A(iv)�̏�Ԃ�(v)�̏�Ԃ̓����G�l���M�[�͓������B���������āA(iv)�̏�Ԃ�(v)�̏�Ԃ̐�1mol������̓����G�l���M�[�����ꂼ��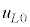 �C
�C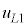 �C(v)�̏�Ԃ̐����C1mol������̓����G�l���M�[��
�C(v)�̏�Ԃ̐����C1mol������̓����G�l���M�[��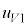 �C(v)�̏�Ԃɂ����鐅���C�̕����ʂ�x�Ƃ���ƁA
�C(v)�̏�Ԃɂ����鐅���C�̕����ʂ�x�Ƃ���ƁA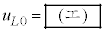 �����藧�B�����A
�����藧�B�����A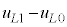 �͐��̔�M
�͐��̔�M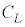 ���܂ގ�
���܂ގ�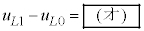 �ŗ^������B
�ŗ^������B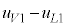 �͑O��(b)�̌��ʂ��l������L���܂ގ��ŕ\�����Ƃ��ł���B������x������G�l���M�[��p���Ȃ����ŕ\����
�͑O��(b)�̌��ʂ��l������L���܂ގ��ŕ\�����Ƃ��ł���B������x������G�l���M�[��p���Ȃ����ŕ\���� �ƂȂ�B
�ƂȂ�B
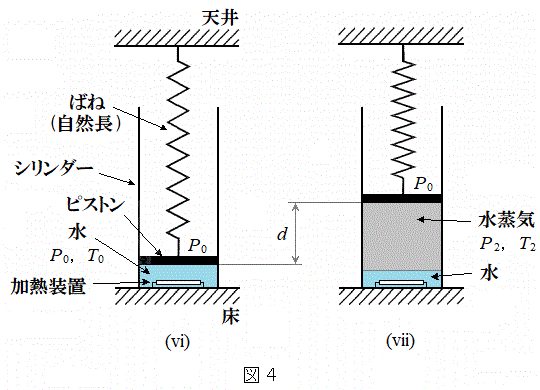 [C]�@�}4(vi)�̂悤�Ɋ��炩�ɓ����s�X�g�������V�����_�[����������
[C]�@�}4(vi)�̂悤�Ɋ��炩�ɓ����s�X�g�������V�����_�[����������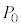 �C���x
�C���x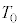 �̐�1mol�Ŗ�������Ă���B�s�X�g���̊O���̈��͂�
�̐�1mol�Ŗ�������Ă���B�s�X�g���̊O���̈��͂�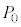 �ł���B�s�X�g���̊O���ɂ́A�˂����t�����Ă���A(vi)�̏�Ԃł́A�˂͎��R���ł���B�����ŁA�˂͓V��ɌŒ肳��Ă���A�V�����_�[�͏��ɌŒ肳��Ă���B���Ƀs�X�g���̊O���̈��͂�
�ł���B�s�X�g���̊O���ɂ́A�˂����t�����Ă���A(vi)�̏�Ԃł́A�˂͎��R���ł���B�����ŁA�˂͓V��ɌŒ肳��Ă���A�V�����_�[�͏��ɌŒ肳��Ă���B���Ƀs�X�g���̊O���̈��͂� �ň��ɕۂ��Ȃ���A���鎞�ԁA���M���u�ł��������M�����Ƃ���A���̈ꕔ���������Đ}4(vii)�̂悤�ɃV�����_�[���͈��͂Ɖ��x����l�ȋC�t������ԂƂȂ����B���̈��͂Ɖ��x��
�ň��ɕۂ��Ȃ���A���鎞�ԁA���M���u�ł��������M�����Ƃ���A���̈ꕔ���������Đ}4(vii)�̂悤�ɃV�����_�[���͈��͂Ɖ��x����l�ȋC�t������ԂƂȂ����B���̈��͂Ɖ��x��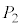 �C
�C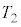 �ł������B�˒萔��k�C�V�����_�[�̒f�ʐς�A�Ƃ��A�ȉ��̖�ɓ�����B�������A�˂̎��ʂƑ����͖����ł�����̂Ƃ���B
�ł������B�˒萔��k�C�V�����_�[�̒f�ʐς�A�Ƃ��A�ȉ��̖�ɓ�����B�������A�˂̎��ʂƑ����͖����ł�����̂Ƃ���B
(d) (vi)�̏�Ԃ���(vii)�̏�Ԃւ̕ω��ɔ����s�X�g���̈ړ��ʂ�d�Ƃ���B(vii)�̏�Ԃɂ�����͂̂荇�����l���āAd�����߂�B
(e) (vii)�̏�Ԃɂ����鐅���C�̕�����x��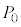 �C
�C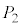 �C
�C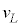 �C
�C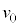 �C
�C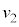 �CA�Cd�̂����K�v�Ȃ��̂�p���ĕ\���B
�CA�Cd�̂����K�v�Ȃ��̂�p���ĕ\���B
(f) (vi)�̏�Ԃ���(vii)�̏�Ԃ܂ŕω�����ۂɁA�V�����_�[���ł̐��̏����ɂƂ��Ȃ��ăs�X�g�����O���ɑ��Ďd���������B���̎d��W��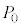 �Cd�CA�Ck�̂����K�v�Ȃ��̂�p���ĕ\���B
�Cd�CA�Ck�̂����K�v�Ȃ��̂�p���ĕ\���B
[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B