���H�啨��'20�N�O��[1]
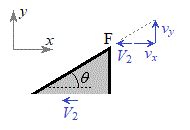
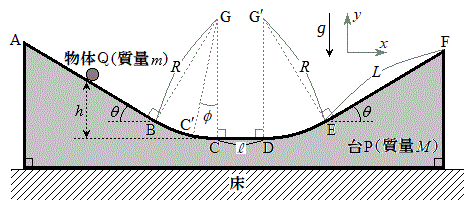 �}�̂悤�ɁA2�̎Ζ�AB(���ɑ���X�Ίpθ)�CEF(����L�C���ɑ���X�Ίpθ)�Ɛ����Ȗ�CD(����
�}�̂悤�ɁA2�̎Ζ�AB(���ɑ���X�Ίpθ)�CEF(����L�C���ɑ���X�Ίpθ)�Ɛ����Ȗ�CD(����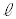 )���A2�̉~�ʖ�BC(���S�_G�C���aR)�CDE(���S�_
)���A2�̉~�ʖ�BC(���S�_G�C���aR)�CDE(���S�_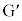 �C���aR)�łȂ߂炩�ɂȂ�����P (����M)�������ȏ��̏�ɒu����Ă���B���̑�P��ɒu���ꂽ�傫���̖����ł��镨��Q (����m)���A�ʂɉ����Ė��C�Ȃ��ɉ^������B�������A�Ζ�AB�̒�����L��蒷���A����Q�͑�P�̒[�_F�ɒB�����Ƃ��ɂ́A��P���痣��邱�Ƃ��ł���Ƃ���B�܂��A��P�C����Q�͂�������}�̉��s�������ɂ͈ړ����Ȃ����̂Ƃ���B����������x�����A����������y�����Ƃ�A���ꂼ��}�̉E�����A������𐳂Ƃ���B��C��R�͖����ł���Ƃ��A�d�͉����x�̑傫����
�C���aR)�łȂ߂炩�ɂȂ�����P (����M)�������ȏ��̏�ɒu����Ă���B���̑�P��ɒu���ꂽ�傫���̖����ł��镨��Q (����m)���A�ʂɉ����Ė��C�Ȃ��ɉ^������B�������A�Ζ�AB�̒�����L��蒷���A����Q�͑�P�̒[�_F�ɒB�����Ƃ��ɂ́A��P���痣��邱�Ƃ��ł���Ƃ���B�܂��A��P�C����Q�͂�������}�̉��s�������ɂ͈ړ����Ȃ����̂Ƃ���B����������x�����A����������y�����Ƃ�A���ꂼ��}�̉E�����A������𐳂Ƃ���B��C��R�͖����ł���Ƃ��A�d�͉����x�̑傫����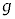 �Ƃ��āA�ȉ��̖�ɓ�����B
�Ƃ��āA�ȉ��̖�ɓ�����B
[A]�@��P�����ɌŒ肳��Ă���ꍇ���l����B
(a) �Ζ�AB��Ŗ�CD�ɑ��č���h�̏ꏊ�ɕ���Q��u���ď����x�Ȃ��ɕ������B����Q�����߂ē_D�ɒB�����Ƃ��̕���Q�̏��ɑ��鑬�x��x���������߂�B
(b) ��(a)�ɂ����āAh������l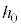 ���傫���Ƃ��A����Q�͒[�_F�ɒB���đ�P���痣��邪�Ah��
���傫���Ƃ��A����Q�͒[�_F�ɒB���đ�P���痣��邪�Ah��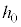 ��菬�����Ƃ��A����Q�͑�P���痣��Ȃ��B���̂悤��
��菬�����Ƃ��A����Q�͑�P���痣��Ȃ��B���̂悤��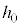 ��m�CM�C
��m�CM�C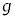 �C
�C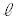 �CR�Cθ�̂����K�v�Ȃ��̂�p���ĕ\���B
�CR�Cθ�̂����K�v�Ȃ��̂�p���ĕ\���B
(c) ��(a)�ɂ����āAh��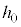 ���傫���Ƃ��A����Q�͒[�_F�ɒB������A��P���痣���B����Q���[�_F�𗣂�Ă���ō��_�ɒB����܂ł̎��Ԃ��Am�CM�C
���傫���Ƃ��A����Q�͒[�_F�ɒB������A��P���痣���B����Q���[�_F�𗣂�Ă���ō��_�ɒB����܂ł̎��Ԃ��Am�CM�C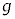 �Ch�C
�Ch�C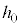 �Cθ�̂����K�v�Ȃ��̂�p���ĕ\���B
�Cθ�̂����K�v�Ȃ��̂�p���ĕ\���B
(d) �~�ʖ�BC��̓_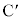 �ɕ���Q��u���ď����x�Ȃ��ɕ������Ƃ���A����Q�͖�CD����ړ����A�~�ʖ�DE��̓_�ɒB������A�������犊��~��čĂѓ_
�ɕ���Q��u���ď����x�Ȃ��ɕ������Ƃ���A����Q�͖�CD����ړ����A�~�ʖ�DE��̓_�ɒB������A�������犊��~��čĂѓ_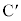 �ɖ߂�����^�����s�����B���̉^���̎����ɂ��ďq�ׂ����̕��͂ɂ����āA��(�A)�`(�G)�ɓ��Ă͂܂鐔������B�������A����
�ɖ߂�����^�����s�����B���̉^���̎����ɂ��ďq�ׂ����̕��͂ɂ����āA��(�A)�`(�G)�ɓ��Ă͂܂鐔������B�������A����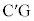 ������CG�ƂȂ��p
������CG�ƂȂ��p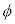 �͏\���ɏ������A����Q�̉~�ʖʏ�̉^���͒P�U���ƌ��Ȃ�����̂Ƃ��A�K�v�Ȃ�
�͏\���ɏ������A����Q�̉~�ʖʏ�̉^���͒P�U���ƌ��Ȃ�����̂Ƃ��A�K�v�Ȃ�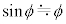 �C
�C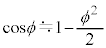 �̋ߎ�����p���Ă悢�B
�̋ߎ�����p���Ă悢�B
����Q���_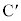 ���珉�߂ē_C�ɒB����܂ł̎��Ԃ�
���珉�߂ē_C�ɒB����܂ł̎��Ԃ� �ł���B�܂��A�_C�ɒB�����Ƃ��̕���Q�̑�����
�ł���B�܂��A�_C�ɒB�����Ƃ��̕���Q�̑�����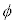 �ɔ�Ⴕ����
�ɔ�Ⴕ���� �ŕ\�����Ƃ��ł���B���̂��Ƃ���A����Q���_C���珉�߂ē_D�ɒB����܂ł̎��Ԃ�
�ŕ\�����Ƃ��ł���B���̂��Ƃ���A����Q���_C���珉�߂ē_D�ɒB����܂ł̎��Ԃ� �ƕ\����B���������āA���̉^���̎�����
�ƕ\����B���������āA���̉^���̎����� �ł���B
�ł���B
[B]�@��P�������痣��邱�ƂȂ����C�Ȃ���x�����Ɉړ��ł���ꍇ���l����B
(e) ��P�����ɑ��ĐÎ~���Ă���Ƃ��A�Ζ�AB��Ŗ�CD�ɑ��č���h�̏ꏊ�ɕ���Q��u���ď����x�Ȃ��ɕ������B����Q�����߂ē_D�ɒB�����Ƃ��̕���Q����ё�P�̏��ɑ��鑬�x��x����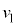 �C
�C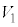 �����ꂼ�ꋁ�߂�B
�����ꂼ�ꋁ�߂�B
(f) ��(e)�ɂ����āAh������l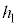 ���傫���Ƃ��A����Q�͒[�_F�ɒB���đ�P���痣��邪�Ah��
���傫���Ƃ��A����Q�͒[�_F�ɒB���đ�P���痣��邪�Ah��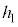 ��菬�����Ƃ��A����Q�͑�P���痣��Ȃ��B���̂悤��
��菬�����Ƃ��A����Q�͑�P���痣��Ȃ��B���̂悤��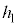 ��m�CM�C
��m�CM�C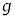 �C
�C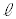 �CR�Cθ�̂����K�v�Ȃ��̂�p���ĕ\���B
�CR�Cθ�̂����K�v�Ȃ��̂�p���ĕ\���B
(g) ��(e)�ɂ����āAh��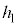 ���傫���Ƃ��A����Q�͒[�_F�ɒB������A��P���痣���B���̏u�Ԃ̑�P�̏��ɑ��鑬�x��x����
���傫���Ƃ��A����Q�͒[�_F�ɒB������A��P���痣���B���̏u�Ԃ̑�P�̏��ɑ��鑬�x��x����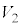 �ɂ��ďq�ׂ����̕��͂ɂ����āA��(�I)�C(�J)�ɓ��Ă͂܂鐔������A
�ɂ��ďq�ׂ����̕��͂ɂ����āA��(�I)�C(�J)�ɓ��Ă͂܂鐔������A ����Q����P���痣���u�Ԃɂ����镨��Q�̏��ɑ��鑬�x��x���������y���������ꂼ��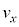 �C
�C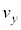 �Ƃ���ƁA����Q���Ζ�EF����^�����Ă������Ƃ���A
�Ƃ���ƁA����Q���Ζ�EF����^�����Ă������Ƃ���A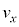 �C
�C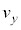 �C
�C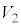 �̊Ԃɂ͎Ζ�EF�̌X�Ίpθ�Ō��܂�W��
�̊Ԃɂ͎Ζ�EF�̌X�Ίpθ�Ō��܂�W�� �����藧�B���̎��ƁA�͊w�I�G�l���M�[�ۑ�������щ^���ʕۑ�����A�����ĉ����ƁA
�����藧�B���̎��ƁA�͊w�I�G�l���M�[�ۑ�������щ^���ʕۑ�����A�����ĉ����ƁA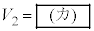 �ƕ\�����B
�ƕ\�����B
[C]�@����Q�̒u���ꂽ��P�����x�����ɉ����xa (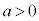 )�̓������x�^�����s���悤�ɁA��P�ɓK�ȊO��T��������ꍇ���l����B��P�́A�����痣��邱�ƂȂ����C�Ȃ���x���̐��̌����ɉ^��������̂Ƃ���B
)�̓������x�^�����s���悤�ɁA��P�ɓK�ȊO��T��������ꍇ���l����B��P�́A�����痣��邱�ƂȂ����C�Ȃ���x���̐��̌����ɉ^��������̂Ƃ���B
(h) �~�ʖ�BC��ɂ��镨��Q���A�_B�CC���邱�ƂȂ���P���猩�ĒP�U���ƌ��Ȃ���\���ɐU���̏����Ȏ����^�����s�����B���̉^���̎��������߂�B
(i) ���ɁA�Ζ�AB��ɕ���Q���u���ꂽ���l����B��P�����ɑ��ċ���s�����ړ������Ă���ԁA����Q�͎Ζ�AB��ʼn^�����Ă����B���̊ԂɊO��T���s�����d���̑傫����m�CM�C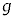 �Cs�Cθ�Ca��p���ĕ\���B
�Cs�Cθ�Ca��p���ĕ\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�قڕp�o�^�C�v�̕W�����ł����A�Ƃ���ǂ��뒚�J�ɍl�@���ׂ��_������܂��B
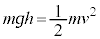 �@��
�@�� 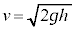 ......[��]
......[��]
(b) 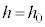 �C�܂�A����Q���[�_F�ł��傤�ǒ�~���镪����ڂ̏��l���܂��B�_B�CE�̖�CD����̍����́A
�C�܂�A����Q���[�_F�ł��傤�ǒ�~���镪����ڂ̏��l���܂��B�_B�CE�̖�CD����̍����́A �_F�̖�CD����̍����́A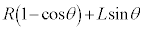 �C����Q�̓_F�ɂ�����ʒu�G�l���M�[��
�C����Q�̓_F�ɂ�����ʒu�G�l���M�[��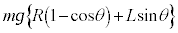 �C�^���G�l���M�[��0�C�����ꂽ�_�ł̈ʒu�G�l���M�[��
�C�^���G�l���M�[��0�C�����ꂽ�_�ł̈ʒu�G�l���M�[��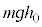 �C�^���G�l���M�[��0�C�͊w�I�G�l���M�[�ۑ����A
�C�^���G�l���M�[��0�C�͊w�I�G�l���M�[�ۑ����A 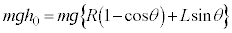 �@��
�@�� 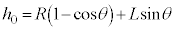 ......[��]
......[��]���̌��ʂ́A�_F�Ɠ��������̂Ƃ���ŕ���Q������ƁA���傤�ǒ[�_F�ŕ���Q����~���邱�Ƃ��Ӗ����Ă��܂��B
(c) 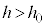 �̂Ƃ��A�[�_F�ɂ����镨��Q�̑�����
�̂Ƃ��A�[�_F�ɂ����镨��Q�̑�����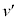 �Ƃ���ƁA���̓_�ł̉^���G�l���M�[��
�Ƃ���ƁA���̓_�ł̉^���G�l���M�[��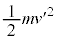 �C�͊w�I�G�l���M�[�ۑ����A
�C�͊w�I�G�l���M�[�ۑ����A 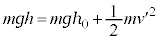 �@��
�@�� 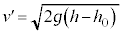
����Q�̑�P���痣�ꂽ����̑��x��y������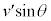 �C���߂鎞�Ԃ�t �Ƃ��āAy�����ɂ��āA�������x�^���̌������A
�C���߂鎞�Ԃ�t �Ƃ��āAy�����ɂ��āA�������x�^���̌������A 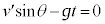 ��
�� 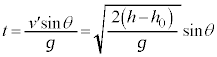 ......[��]
......[��]
(d)(�A) ����Q���~�ʖ�DE��̓_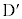 �܂ōs���Ĉ����Ԃ��Ƃ��܂��B
�܂ōs���Ĉ����Ԃ��Ƃ��܂��B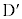 ��CD�ʂ���̍����́A�͊w�I�G�l���M�[�ۑ����A
��CD�ʂ���̍����́A�͊w�I�G�l���M�[�ۑ����A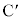 ��CD�ʂ���̍����Ɠ����ł��B�����^���̂����A
��CD�ʂ���̍����Ɠ����ł��B�����^���̂����A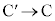 �C
�C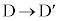 �C
�C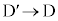 �C
�C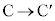 ���Ȃ����^���́A
���Ȃ����^���́A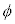 �������ł��邱�Ƃ���A�Ђ��̒���R���P�U��q���P�U����1�������ƍl����ƁA���̎�����
�������ł��邱�Ƃ���A�Ђ��̒���R���P�U��q���P�U����1�������ƍl����ƁA���̎�����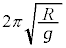 �ł��B����Q��
�ł��B����Q��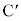 ���珉�߂�C�ɒB����܂ł̎��Ԃ͎�����
���珉�߂�C�ɒB����܂ł̎��Ԃ͎�����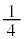 �ŁA
�ŁA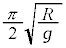 ......[��]
......[��]
(�C) �_C�ɒB�����Ƃ��̕���Q�̑�����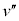 �Ƃ���ƁA����Q�̓_
�Ƃ���ƁA����Q�̓_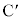 �ɂ�����ʒu�G�l���M�[��
�ɂ�����ʒu�G�l���M�[��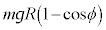 �C�_C�ɂ�����^���G�l���M�[��
�C�_C�ɂ�����^���G�l���M�[��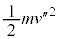 �C�͊w�I�G�l���M�[�ۑ����A
�C�͊w�I�G�l���M�[�ۑ����A 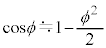 �Ƌߎ�����ƁA
�Ƌߎ�����ƁA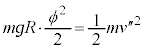 �@��
�@�� 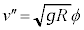 ......[��]
......[��]
(�E) CD�Ԃ͓����x�^������̂ŁA�_C���珉�߂�D�ɒB����܂ł̎��Ԃ́A
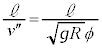 ......[��]
......[��]
(�G) �^���S�̂̎����́A�P�U��q�̎�����CD���������鎞�Ԃ������āA
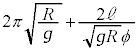 ......[��]
......[��]
[B](e) �����ꂽ�_�ŕ���Q�̈ʒu�G�l���M�[��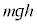 �C�^���G�l���M�[�́A����Q�C��P�Ƃ�0�C�^���ʂ�0�C����Q���_D�ɒB�������_�ŁA����Q�̈ʒu�G�l���M�[��0�C�^���G�l���M�[�́A����Q��
�C�^���G�l���M�[�́A����Q�C��P�Ƃ�0�C�^���ʂ�0�C����Q���_D�ɒB�������_�ŁA����Q�̈ʒu�G�l���M�[��0�C�^���G�l���M�[�́A����Q��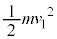 �C��P��
�C��P��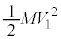 �C���n�_�ł̑�P�̈ʒu�G�l���M�[�ɕω��͂Ȃ��A�͊w�I�G�l���M�[�ۑ����A
�C���n�_�ł̑�P�̈ʒu�G�l���M�[�ɕω��͂Ȃ��A�͊w�I�G�l���M�[�ۑ����A 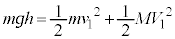 �@����@
�@����@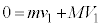 �@��
�@�� 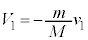 �@����A
�@����A�@�ɑ�����āA
�A���A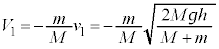 ......[��]
......[��]
(f) (b)���l�A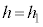 �C�܂�A����Q���[�_F�ł��傤�ǒ�~���镪����ڂ̏��l���܂��B����Q�������ꂽ�Ƃ��A�ʒu�G�l���M�[��
�C�܂�A����Q���[�_F�ł��傤�ǒ�~���镪����ڂ̏��l���܂��B����Q�������ꂽ�Ƃ��A�ʒu�G�l���M�[��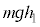 �C���x�͕���Q�C��P�Ƃ�0�ł��B����Q���[�_F�ɒB�����Ƃ��A����Q����P�ɑ��ĐÎ~����A�Ƃ������Ƃ́A����Q�Ƒ�P�̑��x����v���ē����l�ɂȂ�Ƃ������Ƃł��B���̑��x��
�C���x�͕���Q�C��P�Ƃ�0�ł��B����Q���[�_F�ɒB�����Ƃ��A����Q����P�ɑ��ĐÎ~����A�Ƃ������Ƃ́A����Q�Ƒ�P�̑��x����v���ē����l�ɂȂ�Ƃ������Ƃł��B���̑��x��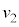 �Ƃ��܂��B���n�_�ł�x�����̉^���ʕۑ����A
�Ƃ��܂��B���n�_�ł�x�����̉^���ʕۑ����A 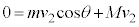 �@��
�@�� 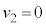
���n�_�ő�P�̈ʒu�G�l���M�[�ɕω��͂Ȃ��A�[�_F�ł̕���Q�̗͊w�I�G�l���M�[�͈ʒu�G�l���M�[��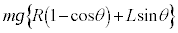 �݂̂ŁA�͊w�I�G�l���M�[�ۑ����A
�݂̂ŁA�͊w�I�G�l���M�[�ۑ����A 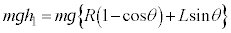 ��
�� 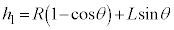 ......[��]
......[��]���̌��ʂ�(b)�Ɠ����ł����A��P�������ꍇ�ł��A�[�_F�Ɠ��������̏����畨��Q������Ƃ��傤�ǒ[�_F�Œ�~����A�Ƃ������Ƃ��Ӗ����Ă��܂��B
 (g)(�I) ��P��Ō��āA����Q���Ζʂɉ����ĉ^�����Ă��Ē[�_F�����яo���u�ԂɁA��P��Ō�������Q�����Α��x��x�����́A
(g)(�I) ��P��Ō��āA����Q���Ζʂɉ����ĉ^�����Ă��Ē[�_F�����яo���u�ԂɁA��P��Ō�������Q�����Α��x��x�����́A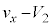 (
(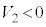 �ɒ���)�Cy������
�ɒ���)�Cy������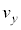 �C�����̊W�͉E�}�̂悤�ɂȂ�A
�C�����̊W�͉E�}�̂悤�ɂȂ�A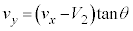 ......[��]�@����B
......[��]�@����B
(�J) 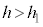 �̂Ƃ��A����Q�������ꂽ�Ƃ��̈ʒu�G�l���M�[��
�̂Ƃ��A����Q�������ꂽ�Ƃ��̈ʒu�G�l���M�[��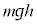 �C�^���G�l���M�[�͕���Q�C��P�Ƃ�0�C�^���ʂ�����Q�C��P�Ƃ�0�C����Q���[�_F�����яo���u�ԂɁA����Q�̈ʒu�G�l���M�[��
�C�^���G�l���M�[�͕���Q�C��P�Ƃ�0�C�^���ʂ�����Q�C��P�Ƃ�0�C����Q���[�_F�����яo���u�ԂɁA����Q�̈ʒu�G�l���M�[��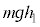 �C�^���G�l���M�[�͕���Q��
�C�^���G�l���M�[�͕���Q��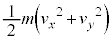 �C��P��
�C��P��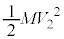 �C���n�_�ő�P�̈ʒu�G�l���M�[�ɕω��͂Ȃ��A�͊w�I�G�l���M�[�ۑ����A
�C���n�_�ő�P�̈ʒu�G�l���M�[�ɕω��͂Ȃ��A�͊w�I�G�l���M�[�ۑ����A 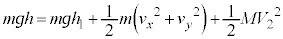 �@����C
�@����Cx�����̉^���ʕۑ����A
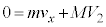 �@��
�@�� 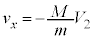 �@����D�C������B�ɑ�����A
�@����D�C������B�ɑ�����A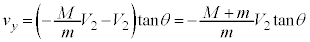
����ƇE���D�ɑ�����A
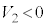 �Ȃ̂ŁA
�Ȃ̂ŁA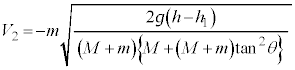 ......[��]
......[��]
[C](h) �Ђ��̒���R�̒P�U��q�̎����F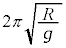 �ɂ����āA�d�͉����x
�ɂ����āA�d�͉����x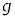 ���������̏d�͉����x
���������̏d�͉����x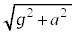 �Ƃ���(���������Q��)�A
�Ƃ���(���������Q��)�A 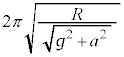 ......[��]
......[��]
(i) �������A�d����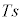 �Ȃ̂ł����AT���g�킸�ɓ�����̂ŁAT�����߂�K�v������܂��B��P��x�����Ɏ�͂́A�O��T�C����Q����Ζʂ��鐂���R��N��x��������
�Ȃ̂ł����AT���g�킸�ɓ�����̂ŁAT�����߂�K�v������܂��B��P��x�����Ɏ�͂́A�O��T�C����Q����Ζʂ��鐂���R��N��x��������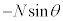 �ł��B��P��x�������^���������F
�ł��B��P��x�������^���������F 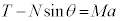 �@����E
�@����E��P��Ō��āA����Q���ΖʂƐ����ȕ����Ɏ�͂́A�Ζʂ���鐂���R��N�C�����������̏d�͂̎ΖʂƐ����ȕ����̐���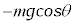 �Cx���������̊����͂̎ΖʂƐ����ȕ����̐���
�Cx���������̊����͂̎ΖʂƐ����ȕ����̐���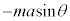 �ł��B�������͂̂荇���F
�ł��B�������͂̂荇���F ������A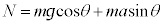 �C������E�ɑ�����āA
�C������E�ɑ�����āA ����āA���߂�d���́A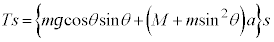 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 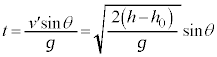 ......[��]
......[��]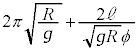 ......[��]
......[��]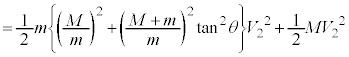
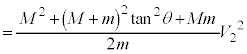
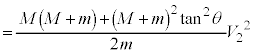
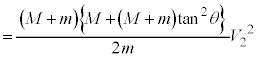
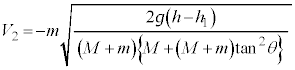 ......[��]
......[��]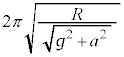 ......[��]
......[��]