�����H�Ƒ�w2024�N�O�������������
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
 [1]�@�}1�̂悤�ȁA��ӂ̒�����
[1]�@�}1�̂悤�ȁA��ӂ̒����� �̗����̂ł���4�̃u���b�NA�C
�̗����̂ł���4�̃u���b�NA�C �C
�C �C
�C �̂����������ƁA���ʂ̖����ł���L�яk�݂��Ȃ�����p���Ď������s���BA��
�̂����������ƁA���ʂ̖����ł���L�яk�݂��Ȃ�����p���Ď������s���BA�� �͎��ʂ̖����ł��闧���̂̈�ӂ̒��_�Ɏ���m�̏��������t����ꂽ���̂ł���BA�͂��ׂĂ̖ʂŊ��炩�ł���̂ɑ��āA
�͎��ʂ̖����ł��闧���̂̈�ӂ̒��_�Ɏ���m�̏��������t����ꂽ���̂ł���BA�͂��ׂĂ̖ʂŊ��炩�ł���̂ɑ��āA �͏����ɐڂ���2�̖ʂ̕Е������炩�ł͂Ȃ��B
�͏����ɐڂ���2�̖ʂ̕Е������炩�ł͂Ȃ��B ��
�� �͂����������
�͂���������� �̋ώ��ȗ����̂ł���B�d�͉����x�̑傫����
�̋ώ��ȗ����̂ł���B�d�͉����x�̑傫���� �Ƃ���B�K�v�ł���Έȉ��̌�����p���Ă悢�B
�Ƃ���B�K�v�ł���Έȉ��̌�����p���Ă悢�B
 [A]�@�}2�̂悤�ɁA�����ȏ��̏��
[A]�@�}2�̂悤�ɁA�����ȏ��̏�� ��
�� ���Ԋu
���Ԋu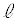 �������Ēu���A�݂��ɂ���݂Ȃ����Ő����ɂȂ����B
�������Ēu���A�݂��ɂ���݂Ȃ����Ő����ɂȂ����B ��
�� �̏�ɁA���������ɂ���A�����E�Ώ̂ɂȂ�悤�ɐÂ��ɒu�����B�}2�ɂ�����3�̃u���b�N�̐��ʂ͓���̉����ʓ��ɂ���B�܂��A����3�̃u���b�N�̒��S���܂ޖʓ��ɂ���B�u���b�N�ǂ����y�уu���b�N�Ə��̊Ԃɖ��C�͂͂��炩�Ȃ��B
�̏�ɁA���������ɂ���A�����E�Ώ̂ɂȂ�悤�ɐÂ��ɒu�����B�}2�ɂ�����3�̃u���b�N�̐��ʂ͓���̉����ʓ��ɂ���B�܂��A����3�̃u���b�N�̒��S���܂ޖʓ��ɂ���B�u���b�N�ǂ����y�уu���b�N�Ə��̊Ԃɖ��C�͂͂��炩�Ȃ��B ��
�� �͂�������X�����Ƃ��Ȃ��Ƃ��āA�ȉ��̖₢�ɓ�����B
�͂�������X�����Ƃ��Ȃ��Ƃ��āA�ȉ��̖₢�ɓ�����B
(a) ���̒��͂̑傫��T�����߂�B
����Â��ɐ�ƁA ��
�� �̊Ԋu���L�����Ă����ƂƂ��ɁAA��������ۂ����܂܉������Ă����A
�̊Ԋu���L�����Ă����ƂƂ��ɁAA��������ۂ����܂܉������Ă����A ��
�� �̊Ԋu��
�̊Ԋu�� �����Ƃ����A��
�����Ƃ����A�� ��
�� ���痣��ė��������B�^�����A�ؒf���ꂽ���̓u���b�N�̉^����W���Ȃ����̂Ƃ���B
���痣��ė��������B�^�����A�ؒf���ꂽ���̓u���b�N�̉^����W���Ȃ����̂Ƃ���B
(b) ��������Ƃ�����AA�� ��
�� ���痣���܂ł̊Ԃ�A�̈ړ����������߂�B
���痣���܂ł̊Ԃ�A�̈ړ����������߂�B
(c) A�����ɐڐG���钼�O��A�̑���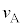 ��
�� �̑���
�̑��� ���A
���A �C
�C �Cm�C
�Cm�C ��p���ĕ\���B
��p���ĕ\���B
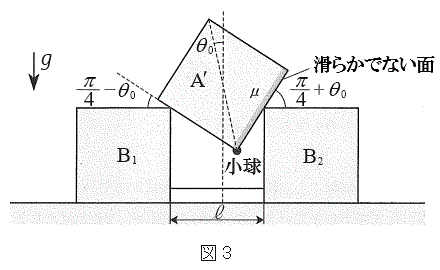 [B]�@�}3�̂悤�ɁA�����ȏ��̏��
[B]�@�}3�̂悤�ɁA�����ȏ��̏�� ��
�� ���Ԋu
���Ԋu �������Ēu���A�݂��ɂ���݂Ȃ����Ő����ɂȂ����B
�������Ēu���A�݂��ɂ���݂Ȃ����Ő����ɂȂ����B ��
�� �̏�ɁA���������ɂ��Ċ��炩�łȂ��ʂ�
�̏�ɁA���������ɂ��Ċ��炩�łȂ��ʂ� �̕ӂɐڂ���悤��
�̕ӂɐڂ���悤�� ���X���ĐÂ��ɒu�����B�}3�ɂ�����3�̃u���b�N�̐��ʂ͓���̉����ʓ��ɂ���B�܂��A����3�̃u���b�N�̒��S���܂މ����ʓ��ɂ���B���̉����ʂɂ��
���X���ĐÂ��ɒu�����B�}3�ɂ�����3�̃u���b�N�̐��ʂ͓���̉����ʓ��ɂ���B�܂��A����3�̃u���b�N�̒��S���܂މ����ʓ��ɂ���B���̉����ʂɂ�� �̒f�ʂɂ����āA���߂�
�̒f�ʂɂ����āA���߂� ���u���ꂽ�Ƃ��ɏ������܂ޑΊp���Ɖ������̂Ȃ��p��
���u���ꂽ�Ƃ��ɏ������܂ޑΊp���Ɖ������̂Ȃ��p�� �Ƃ���B
�Ƃ���B �̏ꍇ�݂̂��l����B�}3�̂悤�ɏ�����
�̏ꍇ�݂̂��l����B�}3�̂悤�ɏ����� ����
���� �ɋ߂��Ƃ��A
�ɋ߂��Ƃ��A �͐��Ƃ���B
�͐��Ƃ���B ������͈͓�
������͈͓� �ɂ���Ƃ��A
�ɂ���Ƃ��A �͐Î~�������A
�͐Î~�������A �ł���ꍇ�ɂ�
�ł���ꍇ�ɂ� �͊����Č�����ω��������B
�͊����Č�����ω��������B ��
�� �̊Ԃ̐Î~���C�W����μ�ł���A����
�̊Ԃ̐Î~���C�W����μ�ł���A���� �C����
�C���� �C
�C ��
�� �̊Ԃɂ͖��C�͂͂��炩�Ȃ��B
�̊Ԃɂ͖��C�͂͂��炩�Ȃ��B ��
�� �͂�������X�����Ƃ��Ȃ��Ƃ��āA�ȉ��̖₢�ɓ�����B
�͂�������X�����Ƃ��Ȃ��Ƃ��āA�ȉ��̖₢�ɓ�����B
(d)  �̂Ƃ��A
�̂Ƃ��A ��
�� �ɋy�ڂ������R�͂̑傫��
�ɋy�ڂ������R�͂̑傫�� ���A
���A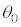 �Cm�C
�Cm�C ��p���ĕ\���B
��p���ĕ\���B
(e)  �̂Ƃ��A
�̂Ƃ��A ��
�� �ɋy�ڂ������R�͂̑傫��
�ɋy�ڂ������R�͂̑傫�� ���A
���A �C
�C ��p���ĕ\���B
��p���ĕ\���B (f)  �̂Ƃ��A
�̂Ƃ��A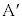 ��
�� �ɋy�ڂ����C�͂̑傫��F���A
�ɋy�ڂ����C�͂̑傫��F���A �Cm�C
�Cm�C ��p���ĕ\���B
��p���ĕ\���B
(g) μ�� ��p���ĕ\���B
��p���ĕ\���B
 [C]�@�}4�̂悤�ɁA�����ȏ��̏��
[C]�@�}4�̂悤�ɁA�����ȏ��̏�� ��
�� ���Ԋu
���Ԋu �������Ēu���A�݂��ɂ���݂Ȃ����Ő����ɂȂ����B�����āA
�������Ēu���A�݂��ɂ���݂Ȃ����Ő����ɂȂ����B�����āA �ƕǂ����ł���݂Ȃ������ɂȂ��A
�ƕǂ����ł���݂Ȃ������ɂȂ��A �͊��炩�Ȋ��Ԃ�ʂ��Ď���M�̂�����Ǝ��łȂ����B���Ԃ�
�͊��炩�Ȋ��Ԃ�ʂ��Ď���M�̂�����Ǝ��łȂ����B���Ԃ� �̊Ԃ̎��͐����ł���B���������ɂ���A��
�̊Ԃ̎��͐����ł���B���������ɂ���A�� ��
�� �̏�ɌX���Ēu���A�Â��ɕ����BM���\���傫���A
�̏�ɌX���Ēu���A�Â��ɕ����BM���\���傫���A ��
�� ����������Î~�����܂܂ł���ꍇ�ɂ́A�����͏�����̍���
����������Î~�����܂܂ł���ꍇ�ɂ́A�����͏�����̍��� �̓_P�𒆐S�Ƃ��ĒP�U��q�Ɠ����^��������B�}4�ɂ�����3�̃u���b�N�̐��ʂ͓���̉����ʓ��ɂ���B�܂��A�_P�y�т��ׂĂ̎���3�̃u���b�N�̒��S���܂މ����ʓ��ɂ���B���̉����ʂɂ��A�̒f�ʂɂ����āA�������܂ޑΊp���Ɖ������̂Ȃ��p��θ�Ƃ���B�}4�̂悤�ɏ�����
�̓_P�𒆐S�Ƃ��ĒP�U��q�Ɠ����^��������B�}4�ɂ�����3�̃u���b�N�̐��ʂ͓���̉����ʓ��ɂ���B�܂��A�_P�y�т��ׂĂ̎���3�̃u���b�N�̒��S���܂މ����ʓ��ɂ���B���̉����ʂɂ��A�̒f�ʂɂ����āA�������܂ޑΊp���Ɖ������̂Ȃ��p��θ�Ƃ���B�}4�̂悤�ɏ����� ����
���� �ɋ߂��Ƃ��Aθ�͐��Ƃ���B�_P�Ə�����ʂ钼���Ɖ������̂Ȃ��p��
�ɋ߂��Ƃ��Aθ�͐��Ƃ���B�_P�Ə�����ʂ钼���Ɖ������̂Ȃ��p�� �ł���B�u���b�N�ǂ����y�уu���b�N�Ə��̊Ԃɖ��C�͂͂��炩�Ȃ��B
�ł���B�u���b�N�ǂ����y�уu���b�N�Ə��̊Ԃɖ��C�͂͂��炩�Ȃ��B ��
�� �͂�������X�����Ƃ͂Ȃ����̂Ƃ���B���߂�A���u���ꂽ�Ƃ���θ��
�͂�������X�����Ƃ͂Ȃ����̂Ƃ���B���߂�A���u���ꂽ�Ƃ���θ�� �Ƃ��A
�Ƃ��A �̏ꍇ�݂̂��l����B�ȉ��̖₢�ɓ�����B
�̏ꍇ�݂̂��l����B�ȉ��̖₢�ɓ�����B�܂��AM���\���傫���AA�̉^�����A ��
�� ����������Î~�����܂܂ł���ꍇ���l����B
����������Î~�����܂܂ł���ꍇ���l����B
(h) �P�U��q�Ɠ����^�������鏬���̑���v���A �C
�C �Cθ�C
�Cθ�C ��p���ĕ\���B�܂��A
��p���ĕ\���B�܂��A ��A�ɋy�ڂ��͂�
��A�ɋy�ڂ��͂� ��A�ɋy�ڂ��͂̍��͂̑傫��G���A
��A�ɋy�ڂ��͂̍��͂̑傫��G���A �Cm�Cθ�C
�Cm�Cθ�C ��p���ĕ\���B
��p���ĕ\���B
(i)  ��
�� ���Ȃ����̒��͂̑傫��
���Ȃ����̒��͂̑傫�� �C�����
�C����� �ƕǂ��Ȃ����̒��͂̑傫��
�ƕǂ��Ȃ����̒��͂̑傫�� ���AG�C
���AG�C �CM�Cθ��p���ĕ\���B
�CM�Cθ��p���ĕ\���B ���ɁA���낢��Ȏ���M�̂������p���Ď�������ƁAM������l �����傫���ꍇ�ɂ͉^���J�n���̊p
�����傫���ꍇ�ɂ͉^���J�n���̊p ��
�� �͈̔͂łǂ̂悤�ɑI��ł�
�͈̔͂łǂ̂悤�ɑI��ł� ��
�� �͓����Ȃ����A
�͓����Ȃ����A �����������ꍇ�ɂ�
�����������ꍇ�ɂ� �̒l�ɂ���Ă�A�̉^����
�̒l�ɂ���Ă�A�̉^���� ��
�� �̗����܂��͂����ꂩ���������B(j)
�̗����܂��͂����ꂩ���������B(j)  ��m��p���ĕ\���B
��m��p���ĕ\���B
[��]
 [2]�@�}1�̂悤�ɁA����r�̓���ab�Ccd�ƒ���
[2]�@�}1�̂悤�ɁA����r�̓���ab�Ccd�ƒ��� �̓���bc�p�ɂȂ��ō�����R�̎��`�̓���X���A�����ɌŒ肳�ꂽ������̓���Y�ɂ艺���č���������`�̉�Habcd���l����BY�̋��ad�̈ꕔ�͓d�r�A��R��A�R�C���A�X�C�b�`�ō�������uZ�Œu�������邱�Ƃ��ł��AY�̗��[�͐≏����Ă���BX��Y�����Ɋ��炩�ɉ�]�ł��邪�A���s�ړ���ό`�����Ȃ����̂Ƃ���B�Ȃ��AY��Z�͓����Ȃ��Bab�Ccd�̎��ʂ͖����ł��Abc�̎��ʂ�m�ł���A�d�͉����x�̑傫����
�̓���bc�p�ɂȂ��ō�����R�̎��`�̓���X���A�����ɌŒ肳�ꂽ������̓���Y�ɂ艺���č���������`�̉�Habcd���l����BY�̋��ad�̈ꕔ�͓d�r�A��R��A�R�C���A�X�C�b�`�ō�������uZ�Œu�������邱�Ƃ��ł��AY�̗��[�͐≏����Ă���BX��Y�����Ɋ��炩�ɉ�]�ł��邪�A���s�ړ���ό`�����Ȃ����̂Ƃ���B�Ȃ��AY��Z�͓����Ȃ��Bab�Ccd�̎��ʂ͖����ł��Abc�̎��ʂ�m�ł���A�d�͉����x�̑傫���� �Ƃ���B�܂��A�������x�̑傫����B�ł��鉔��������̎��ꂪ��l�ɑ��݂��Ă���B�����̑����Ɠd�C��R�A�R�C���ȊO�̎��ȃC���_�N�^���X�A�d�r�̓�����R�A��C��R�͂��ׂĖ����ł�����̂Ƃ���B
�Ƃ���B�܂��A�������x�̑傫����B�ł��鉔��������̎��ꂪ��l�ɑ��݂��Ă���B�����̑����Ɠd�C��R�A�R�C���ȊO�̎��ȃC���_�N�^���X�A�d�r�̓�����R�A��C��R�͂��ׂĖ����ł�����̂Ƃ���B
��H�𗬂��d���̐��̌�����a��b��c��d�ƒ�߂�B�܂��Aa��ʂ鉔�������̒�����ab���Ȃ��p��θ�Ƃ��Aa����b�Ɍ��������������������̂Ƃ��� �ł���Aa��b��c��d�̌����ɉ��E�˂����i�ތ�����θ�̐��̌����ƒ�߂�B����ɁAX�̊p���x��ω�Ƃ��A�����Ȏ���
�ł���Aa��b��c��d�̌����ɉ��E�˂����i�ތ�����θ�̐��̌����ƒ�߂�B����ɁAX�̊p���x��ω�Ƃ��A�����Ȏ��� �̊Ԃ�θ��
�̊Ԃ�θ�� �����ω�����Ƃ��A
�����ω�����Ƃ��A �ł���B
�ł���B
 [A]�@�}2�̂悤�ɁA�d��V�̓d�r�A��R�lR�̒�R��A�X�C�b�`S���g����Z�����Aad�̈ꕔ��u��������B�X�C�b�`��p���ɓ����ƒ�R��݂̂�ʂ��āAq���ɓ����ƒ�R��Ɠd�r��ʂ��ĉ�H������B�d�r�͐��̌����ɓd���𗬂����Ƃ�������ɐݒu����Ă���B�ȉ��̖₢�ɓ�����B
[A]�@�}2�̂悤�ɁA�d��V�̓d�r�A��R�lR�̒�R��A�X�C�b�`S���g����Z�����Aad�̈ꕔ��u��������B�X�C�b�`��p���ɓ����ƒ�R��݂̂�ʂ��āAq���ɓ����ƒ�R��Ɠd�r��ʂ��ĉ�H������B�d�r�͐��̌����ɓd���𗬂����Ƃ�������ɐݒu����Ă���B�ȉ��̖₢�ɓ�����B
(a) �܂��X�C�b�`��p���ɓ���AX�������ɂȂ�悤�� �̈ʒu�܂�bc��������莝���グ���B��H�ɓd��������Ă��Ȃ����Ƃ��m�F���Ă���bc��Â��ɕ������Ƃ���AX��Y�����ɉ^�������B���鎞���ɂ����ĉ�H�𗬂��d��I���Ar�C
�̈ʒu�܂�bc��������莝���グ���B��H�ɓd��������Ă��Ȃ����Ƃ��m�F���Ă���bc��Â��ɕ������Ƃ���AX��Y�����ɉ^�������B���鎞���ɂ����ĉ�H�𗬂��d��I���Ar�C �CB�CR�Cθ�Cω�̂����K�v�ȋL����p���ĕ\���B
�CB�CR�Cθ�Cω�̂����K�v�ȋL����p���ĕ\���B
(b) ��(a)�ɂ����āAab�Cbc�Ccd�����ꂩ���͂̑傫�� �C
�C �C
�C ���A���ꂼ��r�C
���A���ꂼ��r�C �CB�C
�CB�C �C
�C �̂����K�v�ȋL����p���ĕ\���B
�̂����K�v�ȋL����p���ĕ\���B
(c) �\���ɒ������Ԃ��o�ƁA �̈ʒu��X�͐Î~�����Bbc������Ă���
�̈ʒu��X�͐Î~�����Bbc������Ă��� �̈ʒu��X���Î~����܂ł̊Ԃɒ�R�Ŕ��������W���[���MQ���Ar�C
�̈ʒu��X���Î~����܂ł̊Ԃɒ�R�Ŕ��������W���[���MQ���Ar�C �Cm�C
�Cm�C �CB�CR�̂����K�v�ȋL����p���ĕ\���B
�CB�CR�̂����K�v�ȋL����p���ĕ\���B
(d)  �̈ʒu��X���Î~������ԂŃX�C�b�`��q���ɓ��ꂽ�Ƃ���AX��Y�����ɉ^�������A�\���ɒ������Ԃ��o��
�̈ʒu��X���Î~������ԂŃX�C�b�`��q���ɓ��ꂽ�Ƃ���AX��Y�����ɉ^�������A�\���ɒ������Ԃ��o�� �̈ʒu��X�͐Î~�����B���̂Ƃ�
�̈ʒu��X�͐Î~�����B���̂Ƃ� ���Ar�C
���Ar�C �Cm�C
�Cm�C �CB�CV�CR�̂����K�v�ȋL����p���ĕ\���B
�CB�CV�CR�̂����K�v�ȋL����p���ĕ\���B
 [B]�@�}3�̂悤�ɁA���ȃC���_�N�^���XL�̃R�C���ƃX�C�b�`S���g����Z�����Aad�̈ꕔ��u��������B�X�C�b�`������ƃR�C����ʂ��ĉ�H������B�X�C�b�`�������Ԃ�X�������ɂȂ�悤��
[B]�@�}3�̂悤�ɁA���ȃC���_�N�^���XL�̃R�C���ƃX�C�b�`S���g����Z�����Aad�̈ꕔ��u��������B�X�C�b�`������ƃR�C����ʂ��ĉ�H������B�X�C�b�`�������Ԃ�X�������ɂȂ�悤�� �̈ʒu�܂�bc��������莝���グ���B���̌�A�X�C�b�`�����Ă���bc��Â��ɕ������Ƃ���AX��Y������
�̈ʒu�܂�bc��������莝���グ���B���̌�A�X�C�b�`�����Ă���bc��Â��ɕ������Ƃ���AX��Y������ ��
�� �̊Ԃ�������������I�ȉ^���������B�ȉ��̖₢�ɓ�����B
�̊Ԃ�������������I�ȉ^���������B�ȉ��̖₢�ɓ�����B
(e)  �ƂȂ�u�Ԃɉ�H�𗬂��d��
�ƂȂ�u�Ԃɉ�H�𗬂��d��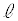 �̑傫�����G�l���M�[�ۑ������狁�߁Ar�C
�̑傫�����G�l���M�[�ۑ������狁�߁Ar�C �Cm�C
�Cm�C �CL�C
�CL�C �̂����K�v�ȋL����p���ĕ\���B
�̂����K�v�ȋL����p���ĕ\���B
(f) �ȉ��̕��͒��̋�(�A)�`(�G)�ɂ��Ă͂܂鐔���܂��͐��l����B�������A(�A)�́Ar�C �CB�CL�Cθ�C
�CB�CL�Cθ�C �C(�C)�`(�G)��r�C
�C(�C)�`(�G)��r�C �CB�CL�̂����K�v�ȋL����p���ĕ\���B
�CB�CL�̂����K�v�ȋL����p���ĕ\���B
���鎞����������Ȏ��� �̊Ԃ�θ��
�̊Ԃ�θ�� �����ω�����Ƃ��A�d��I�̕ω�
�����ω�����Ƃ��A�d��I�̕ω� ��
�� �Ƌ��܂�Bθ��
�Ƌ��܂�Bθ�� �����ω�����Ƃ���
�����ω�����Ƃ��� �̕ω���
�̕ω��� �ł��邱�Ƃ�p����ƁAI�̕ω���
�ł��邱�Ƃ�p����ƁAI�̕ω��� �̕ω��͓��������Ƃ��킩��B����āA���҂̍��ł���
�̕ω��͓��������Ƃ��킩��B����āA���҂̍��ł��� �͎����ɂ��Ȃ��萔�ƂȂ�B����
�͎����ɂ��Ȃ��萔�ƂȂ�B���� �̂Ƃ�
�̂Ƃ� �ł��邱�Ƃ���A
�ł��邱�Ƃ���A �ƒ�܂�̂ŁA�C�ӂ̎����ɂ�����
�ƒ�܂�̂ŁA�C�ӂ̎����ɂ����� �����藧�B
�����藧�B  (g)
(g)  �ƂȂ�悤�Ȏ������x�̑傫��
�ƂȂ�悤�Ȏ������x�̑傫�� ���Ar�C
���Ar�C �Cm�C
�Cm�C �CL�̂����K�v�ȋL����p���ĕ\���B�������A������������ꍇ�ɂ͂��ׂẲ�����A�����Ȃ��ꍇ�ɂ́u
�CL�̂����K�v�ȋL����p���ĕ\���B�������A������������ꍇ�ɂ͂��ׂẲ�����A�����Ȃ��ꍇ�ɂ́u �����Ȃ��v�Ɖ���B
�����Ȃ��v�Ɖ���B
�܂��A ��B�̊��Ƃ��ĕ\�����O���t�̊T�`�Ƃ��čł��K�Ȃ��̂�}4�̑I�����@�`�G����I�сA�ԍ��œ�����B
��B�̊��Ƃ��ĕ\�����O���t�̊T�`�Ƃ��čł��K�Ȃ��̂�}4�̑I�����@�`�G����I�сA�ԍ��œ�����B
[��]
 [3]�@�}1�̂悤�ɃV�����_�[�ƃs�X�g���y�щ��x���ߋ@����Ȃ鑕�u�ɗ��z�C��1mol����������Ă���B�K�v�ɉ����ĉ��x���ߋ@�ɂ��C�̂����M���邢�͗�p������̂Ƃ���B������Ԃ�̐�
[3]�@�}1�̂悤�ɃV�����_�[�ƃs�X�g���y�щ��x���ߋ@����Ȃ鑕�u�ɗ��z�C��1mol����������Ă���B�K�v�ɉ����ĉ��x���ߋ@�ɂ��C�̂����M���邢�͗�p������̂Ƃ���B������Ԃ�̐� �C����
�C���� �C���x
�C���x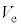 (���0)�Ƃ���B���0����}2�Ɏ����̐�
(���0)�Ƃ���B���0����}2�Ɏ����̐� (
(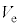 )�̏�Ԃւ̈ȉ���3�ʂ�̕ω����l����B
)�̏�Ԃւ̈ȉ���3�ʂ�̕ω����l����B
�E�舳�ω��F�ω���̑̐� �C����
�C���� �C���x
�C���x (���1)
(���1) �E�����ω��F�ω���̑̐� �C����
�C���� �C���x
�C���x (���2)
(���2) �E�f�M�ω��F�ω���̑̐� �C����
�C���� �C���x
�C���x (���3)
(���3) �����ŁA�舳������M�� �C��σ�����M��
�C��σ�����M�� �Ƃ��A��M���
�Ƃ��A��M��� �C�̐ϔ��
�C�̐ϔ�� �Ƃ���B�Ȃ��A�V�����_�[�ƃs�X�g���̊Ԃɂ͖��C�͂Ȃ����̂Ƃ���B����ɁA�C�̂̓V�����_�[�y�уs�X�g���ƔM�̂��������Ȃ����̂Ƃ���B
�Ƃ���B�Ȃ��A�V�����_�[�ƃs�X�g���̊Ԃɂ͖��C�͂Ȃ����̂Ƃ���B����ɁA�C�̂̓V�����_�[�y�уs�X�g���ƔM�̂��������Ȃ����̂Ƃ���B
[A]�@�舳�ω��A�����ω��A�f�M�ω��ɂ����ċC�̂��O���ɂ���d�������ꂼ�� �C
�C �C
�C �Ƃ��A�舳�ω��y�ѓ����ω��ɂ����ċC�̂ɉ�����M�ʂ����ꂼ��
�Ƃ��A�舳�ω��y�ѓ����ω��ɂ����ċC�̂ɉ�����M�ʂ����ꂼ�� �C
�C �Ƃ���B�ȉ��̖₢�ɓ�����B
�Ƃ���B�ȉ��̖₢�ɓ�����B
(a) �舳�ω��A�����ω��A�f�M�ω��̊T��������p-V�}�Ƃ��ĕ`���B�����āA �C
�C �C
�C �̑召�W��s�����ŕ\���B
�̑召�W��s�����ŕ\���B (b)  �y��
�y�� ��
�� �C
�C ��p���������A���邢�͐��l�ŕ\���B
��p���������A���邢�͐��l�ŕ\���B
[B]�@���0������3�ւ̒f�M�ω���p�����M�@�ւ��l����B���0������3�ւ̒f�M�ω��̌�A���͂� �ɕۂ��Ȃ���A�̐ς�
�ɕۂ��Ȃ���A�̐ς� ����
���� �ɖ߂��B�����ŁA����
�ɖ߂��B�����ŁA���� �C�̐�
�C�̐� �̏�Ԃ����4�Ƃ��A���̉��x��
�̏�Ԃ����4�Ƃ��A���̉��x�� �Ƃ���B���̌�A�̐ς�
�Ƃ���B���̌�A�̐ς� �ɕۂ��Ȃ���C�̂ɔM��Q�������A���4������0�ɖ߂��B�ȉ��̖₢�ɓ�����B
�ɕۂ��Ȃ���C�̂ɔM��Q�������A���4������0�ɖ߂��B�ȉ��̖₢�ɓ�����B
(c) ��[A]�� ��Q�̔�
��Q�̔� ��a��γ��p���ĕ\���B
��a��γ��p���ĕ\���B
(d) ���̔M�@�ւ̔M���� ��a��γ��p����ƈȉ��̂悤�ɕ\�����B��(�A)�ɂ��Ă͂܂鐔������B
��a��γ��p����ƈȉ��̂悤�ɕ\�����B��(�A)�ɂ��Ă͂܂鐔������B
[C]�@���0������2�ւ̓����ω���p�����M�@�ւ��l����B�����ŏ��0������2�ւ̓����ω��ɂ����ċC�̂��O���ɂ���d���� (e�͎��R�ΐ��̒�)�ƕ\�����B���̓����ω���̏��2 (����
(e�͎��R�ΐ��̒�)�ƕ\�����B���̓����ω���̏��2 (���� )����A�̐ς�
)����A�̐ς� �ɕۂ��Ȃ�����3(����
�ɕۂ��Ȃ�����3(���� )�܂ŕω������A���̌㈳�͂�
)�܂ŕω������A���̌㈳�͂� �ɕۂ��Ȃ���̐ς�
�ɕۂ��Ȃ���̐ς� ����
���� �ɖ߂��B���Ȃ킿��[B]�Ɠ��l�ɉ��x
�ɖ߂��B���Ȃ킿��[B]�Ɠ��l�ɉ��x �̏��4�܂ŕω�������B���̌�A�̐ς�
�̏��4�܂ŕω�������B���̌�A�̐ς� �ɕۂ��Ȃ���C�̂ɔM��Q�������A���4������0�ɖ߂��B�ȉ��̖₢�ɓ�����B
�ɕۂ��Ȃ���C�̂ɔM��Q�������A���4������0�ɖ߂��B�ȉ��̖₢�ɓ�����B
(e) ���2������3�ւ̕ω��ɂ����ċC�̂����o����M�� ��
�� �C
�C �Cγ�Ca��p���ĕ\���B�������A�C�̂��M���z������ꍇ�ɂ͔M�ʂ͕��Ƃ���B
�Cγ�Ca��p���ĕ\���B�������A�C�̂��M���z������ꍇ�ɂ͔M�ʂ͕��Ƃ���B
(f) ���̔M�@�ւ̔M���� ��a��γ��p����ƈȉ��̂悤�ɕ\�����B��(�C)��(�E)�ɂ��Ă͂܂鐔������B
��a��γ��p����ƈȉ��̂悤�ɕ\�����B��(�C)��(�E)�ɂ��Ă͂܂鐔������B
[D]�@���0������1�ւ̒舳�ω���p�����M�@�ւ��l����B���̒舳�ω���̏��1(���� )����A�̐ς�
)����A�̐ς� �ɕۂ��Ȃ�����3(����
�ɕۂ��Ȃ�����3(���� )�܂ŕω������A���̌㈳�͂�
)�܂ŕω������A���̌㈳�͂� �ɕۂ��Ȃ���̐ς�
�ɕۂ��Ȃ���̐ς� ����
���� �ɖ߂��B���Ȃ킿�A��[B]�y�і�[C]�Ɠ��l�ɉ��x
�ɖ߂��B���Ȃ킿�A��[B]�y�і�[C]�Ɠ��l�ɉ��x �̏��4�܂ŕω�������B���̌�A�̐ς�
�̏��4�܂ŕω�������B���̌�A�̐ς� �ɕۂ��Ȃ���C�̂ɔM��Q�������A���4������0�ɖ߂��B�ȉ��̖₢�ɓ�����B
�ɕۂ��Ȃ���C�̂ɔM��Q�������A���4������0�ɖ߂��B�ȉ��̖₢�ɓ�����B
(g) ���̔M�@�ւ̔M���� ��a��γ��p����ƈȉ��̂悤�ɕ\�����B��(�G)�ɂ��Ă͂܂鐔������B
��a��γ��p����ƈȉ��̂悤�ɕ\�����B��(�G)�ɂ��Ă͂܂鐔������B
(h)  �y��
�y�� �Ƃ��āA���̔M�@�ւ̔M����
�Ƃ��āA���̔M�@�ւ̔M���� �ƁA��[B]�y�і�[C]�ɂ�����M�@�ւ̔M����
�ƁA��[B]�y�і�[C]�ɂ�����M�@�ւ̔M���� ��
�� ��3�̑召�W��s�����ŕ\���B�K�v�ɉ����āA
��3�̑召�W��s�����ŕ\���B�K�v�ɉ����āA �ł��邱�Ƃ�p���Ă悢�B
[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  �C�̐ϔ��
�C�̐ϔ��


 �C
�C �C
�C