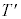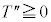���H�啨��'24�N�O��[1]
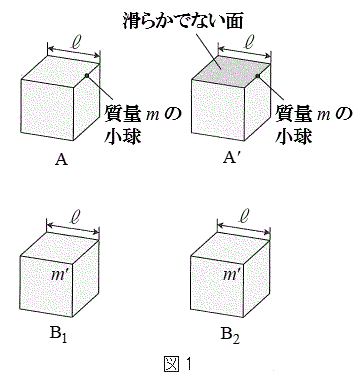 �}1�̂悤�ȁA��ӂ̒�����
�}1�̂悤�ȁA��ӂ̒����� �̗����̂ł���4�̃u���b�NA�C
�̗����̂ł���4�̃u���b�NA�C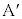 �C
�C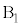 �C
�C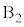 �̂����������ƁA���ʂ̖����ł���L�яk�݂��Ȃ�����p���Ď������s���BA��
�̂����������ƁA���ʂ̖����ł���L�яk�݂��Ȃ�����p���Ď������s���BA��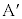 �͎��ʂ̖����ł��闧���̂̈�ӂ̒��_�Ɏ���m�̏��������t����ꂽ���̂ł���BA�͂��ׂĂ̖ʂŊ��炩�ł���̂ɑ��āA
�͎��ʂ̖����ł��闧���̂̈�ӂ̒��_�Ɏ���m�̏��������t����ꂽ���̂ł���BA�͂��ׂĂ̖ʂŊ��炩�ł���̂ɑ��āA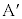 �͏����ɐڂ���2�̖ʂ̕Е������炩�ł͂Ȃ��B
�͏����ɐڂ���2�̖ʂ̕Е������炩�ł͂Ȃ��B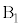 ��
��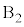 �͂����������
�͂����������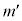 �̋ώ��ȗ����̂ł���B�d�͉����x�̑傫����
�̋ώ��ȗ����̂ł���B�d�͉����x�̑傫���� �Ƃ���B�K�v�ł���Έȉ��̌�����p���Ă悢�B
�Ƃ���B�K�v�ł���Έȉ��̌�����p���Ă悢�B
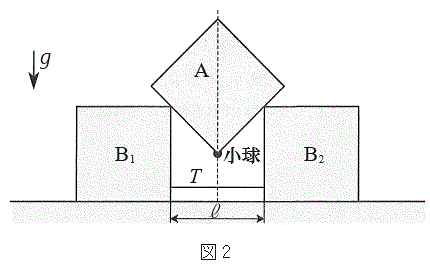 [A]�@�}2�̂悤�ɁA�����ȏ��̏��
[A]�@�}2�̂悤�ɁA�����ȏ��̏�� ��
�� ���Ԋu
���Ԋu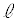 �������Ēu���A�݂��ɂ���݂Ȃ����Ő����ɂȂ����B
�������Ēu���A�݂��ɂ���݂Ȃ����Ő����ɂȂ����B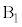 ��
��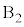 �̏�ɁA���������ɂ���A�����E�Ώ̂ɂȂ�悤�ɐÂ��ɒu�����B�}2�ɂ�����3�̃u���b�N�̐��ʂ͓���̉����ʓ��ɂ���B�܂��A����3�̃u���b�N�̒��S���܂ޖʓ��ɂ���B�u���b�N�ǂ����y�уu���b�N�Ə��̊Ԃɖ��C�͂͂��炩�Ȃ��B
�̏�ɁA���������ɂ���A�����E�Ώ̂ɂȂ�悤�ɐÂ��ɒu�����B�}2�ɂ�����3�̃u���b�N�̐��ʂ͓���̉����ʓ��ɂ���B�܂��A����3�̃u���b�N�̒��S���܂ޖʓ��ɂ���B�u���b�N�ǂ����y�уu���b�N�Ə��̊Ԃɖ��C�͂͂��炩�Ȃ��B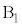 ��
��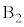 �͂�������X�����Ƃ��Ȃ��Ƃ��āA�ȉ��̖₢�ɓ�����B
�͂�������X�����Ƃ��Ȃ��Ƃ��āA�ȉ��̖₢�ɓ�����B
(a) ���̒��͂̑傫��T�����߂�B
����Â��ɐ�ƁA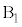 ��
��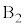 �̊Ԋu���L�����Ă����ƂƂ��ɁAA��������ۂ����܂܉������Ă����A
�̊Ԋu���L�����Ă����ƂƂ��ɁAA��������ۂ����܂܉������Ă����A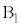 ��
��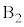 �̊Ԋu��
�̊Ԋu��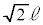 �����Ƃ����A��
�����Ƃ����A��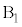 ��
��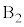 ���痣��ė��������B�^�����A�ؒf���ꂽ���̓u���b�N�̉^����W���Ȃ����̂Ƃ���B
���痣��ė��������B�^�����A�ؒf���ꂽ���̓u���b�N�̉^����W���Ȃ����̂Ƃ���B
(b) ��������Ƃ�����AA��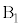 ��
��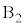 ���痣���܂ł̊Ԃ�A�̈ړ����������߂�B
���痣���܂ł̊Ԃ�A�̈ړ����������߂�B
(c) A�����ɐڐG���钼�O��A�̑���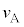 ��
��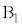 �̑���
�̑���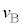 ���A
���A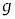 �C
�C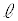 �Cm�C
�Cm�C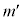 ��p���ĕ\���B
��p���ĕ\���B
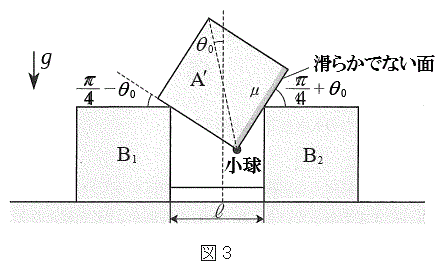 [B]�@�}3�̂悤�ɁA�����ȏ��̏��
[B]�@�}3�̂悤�ɁA�����ȏ��̏��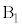 ��
�� ���Ԋu
���Ԋu �������Ēu���A�݂��ɂ���݂Ȃ����Ő����ɂȂ����B
�������Ēu���A�݂��ɂ���݂Ȃ����Ő����ɂȂ����B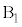 ��
��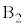 �̏�ɁA���������ɂ��Ċ��炩�łȂ��ʂ�
�̏�ɁA���������ɂ��Ċ��炩�łȂ��ʂ�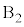 �̕ӂɐڂ���悤��
�̕ӂɐڂ���悤��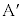 ���X���ĐÂ��ɒu�����B�}3�ɂ�����3�̃u���b�N�̐��ʂ͓���̉����ʓ��ɂ���B�܂��A����3�̃u���b�N�̒��S���܂މ����ʓ��ɂ���B���̉����ʂɂ��
���X���ĐÂ��ɒu�����B�}3�ɂ�����3�̃u���b�N�̐��ʂ͓���̉����ʓ��ɂ���B�܂��A����3�̃u���b�N�̒��S���܂މ����ʓ��ɂ���B���̉����ʂɂ��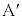 �̒f�ʂɂ����āA���߂�
�̒f�ʂɂ����āA���߂�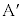 ���u���ꂽ�Ƃ��ɏ������܂ޑΊp���Ɖ������̂Ȃ��p��
���u���ꂽ�Ƃ��ɏ������܂ޑΊp���Ɖ������̂Ȃ��p��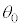 �Ƃ���B
�Ƃ���B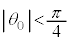 �̏ꍇ�݂̂��l����B�}3�̂悤�ɏ�����
�̏ꍇ�݂̂��l����B�}3�̂悤�ɏ�����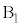 ����
����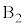 �ɋ߂��Ƃ��A
�ɋ߂��Ƃ��A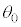 �͐��Ƃ���B
�͐��Ƃ���B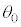 ������͈͓�
������͈͓�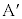 �ɂ���Ƃ��A
�ɂ���Ƃ��A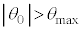 �͐Î~�������A
�͐Î~�������A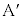 �ł���ꍇ�ɂ�
�ł���ꍇ�ɂ�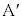 �͊����Č�����ω��������B
�͊����Č�����ω��������B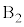 ��
��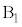 �̊Ԃ̐Î~���C�W����μ�ł���A����
�̊Ԃ̐Î~���C�W����μ�ł���A����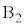 �C����
�C����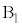 �C
�C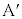 ��
��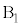 �̊Ԃɂ͖��C�͂͂��炩�Ȃ��B
�̊Ԃɂ͖��C�͂͂��炩�Ȃ��B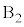 ��
��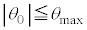 �͂�������X�����Ƃ��Ȃ��Ƃ��āA�ȉ��̖₢�ɓ�����B
�͂�������X�����Ƃ��Ȃ��Ƃ��āA�ȉ��̖₢�ɓ�����B
(d) 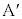 �̂Ƃ��A
�̂Ƃ��A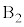 ��
��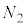 �ɋy�ڂ������R�͂̑傫��
�ɋy�ڂ������R�͂̑傫��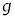 ���A
���A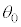 �Cm�C
�Cm�C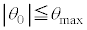 ��p���ĕ\���B
��p���ĕ\���B
(e) 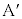 �̂Ƃ��A
�̂Ƃ��A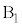 ��
��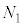 �ɋy�ڂ������R�͂̑傫��
�ɋy�ڂ������R�͂̑傫��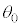 ���A
���A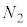 �C
�C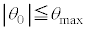 ��p���ĕ\���B
��p���ĕ\���B (f) 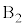 �̂Ƃ��A
�̂Ƃ��A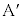 ��
��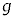 �ɋy�ڂ����C�͂̑傫��F���A
�ɋy�ڂ����C�͂̑傫��F���A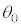 �Cm�C
�Cm�C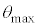 ��p���ĕ\���B
��p���ĕ\���B
(g) μ�� ��p���ĕ\���B
��p���ĕ\���B
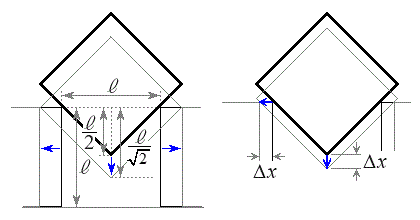
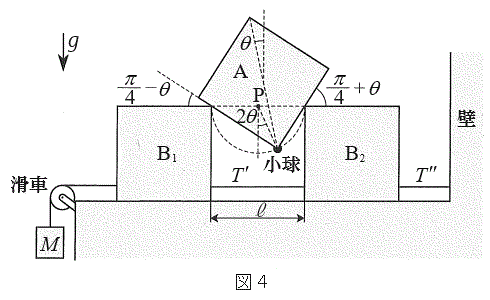 [C]�@�}4�̂悤�ɁA�����ȏ��̏��
[C]�@�}4�̂悤�ɁA�����ȏ��̏�� ��
��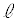 ���Ԋu
���Ԋu �������Ēu���A�݂��ɂ���݂Ȃ����Ő����ɂȂ����B�����āA
�������Ēu���A�݂��ɂ���݂Ȃ����Ő����ɂȂ����B�����āA �ƕǂ����ł���݂Ȃ������ɂȂ��A
�ƕǂ����ł���݂Ȃ������ɂȂ��A �͊��炩�Ȋ��Ԃ�ʂ��Ď���M�̂�����Ǝ��łȂ����B���Ԃ�
�͊��炩�Ȋ��Ԃ�ʂ��Ď���M�̂�����Ǝ��łȂ����B���Ԃ�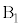 �̊Ԃ̎��͐����ł���B���������ɂ���A��
�̊Ԃ̎��͐����ł���B���������ɂ���A��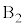 ��
��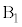 �̏�ɌX���Ēu���A�Â��ɕ����BM���\���傫���A
�̏�ɌX���Ēu���A�Â��ɕ����BM���\���傫���A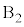 ��
��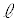 ����������Î~�����܂܂ł���ꍇ�ɂ́A�����͏�����̍���
����������Î~�����܂܂ł���ꍇ�ɂ́A�����͏�����̍���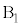 �̓_P�𒆐S�Ƃ��ĒP�U��q�Ɠ����^��������B�}4�ɂ�����3�̃u���b�N�̐��ʂ͓���̉����ʓ��ɂ���B�܂��A�_P�y�т��ׂĂ̎���3�̃u���b�N�̒��S���܂މ����ʓ��ɂ���B���̉����ʂɂ��A�̒f�ʂɂ����āA�������܂ޑΊp���Ɖ������̂Ȃ��p��θ�Ƃ���B�}4�̂悤�ɏ�����
�̓_P�𒆐S�Ƃ��ĒP�U��q�Ɠ����^��������B�}4�ɂ�����3�̃u���b�N�̐��ʂ͓���̉����ʓ��ɂ���B�܂��A�_P�y�т��ׂĂ̎���3�̃u���b�N�̒��S���܂މ����ʓ��ɂ���B���̉����ʂɂ��A�̒f�ʂɂ����āA�������܂ޑΊp���Ɖ������̂Ȃ��p��θ�Ƃ���B�}4�̂悤�ɏ�����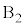 ����
����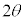 �ɋ߂��Ƃ��Aθ�͐��Ƃ���B�_P�Ə�����ʂ钼���Ɖ������̂Ȃ��p��
�ɋ߂��Ƃ��Aθ�͐��Ƃ���B�_P�Ə�����ʂ钼���Ɖ������̂Ȃ��p��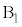 �ł���B�u���b�N�ǂ����y�уu���b�N�Ə��̊Ԃɖ��C�͂͂��炩�Ȃ��B
�ł���B�u���b�N�ǂ����y�уu���b�N�Ə��̊Ԃɖ��C�͂͂��炩�Ȃ��B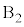 ��
��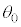 �͂�������X�����Ƃ͂Ȃ����̂Ƃ���B���߂�A���u���ꂽ�Ƃ���θ��
�͂�������X�����Ƃ͂Ȃ����̂Ƃ���B���߂�A���u���ꂽ�Ƃ���θ��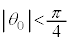 �Ƃ��A
�Ƃ��A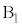 �̏ꍇ�݂̂��l����B�ȉ��̖₢�ɓ�����B
�̏ꍇ�݂̂��l����B�ȉ��̖₢�ɓ�����B�܂��AM���\���傫���AA�̉^�����A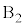 ��
��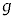 ����������Î~�����܂܂ł���ꍇ���l����B
����������Î~�����܂܂ł���ꍇ���l����B
(h) �P�U��q�Ɠ����^�������鏬���̑���v���A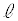 �C
�C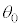 �Cθ�C
�Cθ�C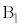 ��p���ĕ\���B�܂��A
��p���ĕ\���B�܂��A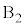 ��A�ɋy�ڂ��͂�
��A�ɋy�ڂ��͂�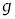 ��A�ɋy�ڂ��͂̍��͂̑傫��G���A
��A�ɋy�ڂ��͂̍��͂̑傫��G���A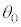 �Cm�Cθ�C
�Cm�Cθ�C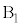 ��p���ĕ\���B
��p���ĕ\���B
(i) 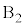 ��
��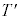 ���Ȃ����̒��͂̑傫��
���Ȃ����̒��͂̑傫��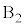 �C�����
�C�����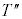 �ƕǂ��Ȃ����̒��͂̑傫��
�ƕǂ��Ȃ����̒��͂̑傫��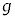 ���AG�C
���AG�C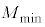 �CM�Cθ��p���ĕ\���B
�CM�Cθ��p���ĕ\���B ���ɁA���낢��Ȏ���M�̂������p���Ď�������ƁAM������l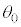 �����傫���ꍇ�ɂ͉^���J�n���̊p
�����傫���ꍇ�ɂ͉^���J�n���̊p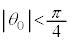 ��
�� �͈̔͂łǂ̂悤�ɑI��ł�
�͈̔͂łǂ̂悤�ɑI��ł� ��
��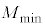 �͓����Ȃ����A
�͓����Ȃ����A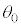 �����������ꍇ�ɂ�
�����������ꍇ�ɂ�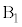 �̒l�ɂ���Ă�A�̉^����
�̒l�ɂ���Ă�A�̉^����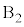 ��
��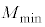 �̗����܂��͂����ꂩ���������B(j)
�̗����܂��͂����ꂩ���������B(j) 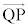 ��m��p���ĕ\���B
��m��p���ĕ\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�ڐV�����̖��ł����A[C]�̖�蕶�́A�㑫�炸�ȏ�Ɍ���������u�P�U��q�v(�P�U���Ǝv�����ނƁA(h)�͍s���l��܂�)�Ƃ����L�q�̂��߂ɖ����ȋC�����܂��B�����ƏJ�ɐ������Ȃ��ƁA���܂��ܗ��R���Ȃ�����G�� �����Ƃ����������������ł����ȊO�ɐ����҂͂��Ȃ��̂ł͂Ȃ����Ǝv���܂��B�܂��A[B]�C[C]�́A��
�����Ƃ����������������ł����ȊO�ɐ����҂͂��Ȃ��̂ł͂Ȃ����Ǝv���܂��B�܂��A[B]�C[C]�́A�� ���c���Ă悢�̂��A�Ƃ������Ƃɂ��Ă��A�w�����Ȃ��Ǝ��̍����������悤�ȋC�����܂��B
���c���Ă悢�̂��A�Ƃ������Ƃɂ��Ă��A�w�����Ȃ��Ǝ��̍����������悤�ȋC�����܂��B
[A](a) A ��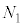 �̊Ԃ������R����
�̊Ԃ������R���� �Ƃ��܂��B�����R�͂Ɛ��������̂Ȃ��p��
�Ƃ��܂��B�����R�͂Ɛ��������̂Ȃ��p��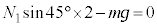 �ł��BA�ɉ��������ɓ����͂̂荇�����A
�ł��BA�ɉ��������ɓ����͂̂荇�����A 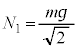 �@��
�@��  �@����@
�@����@ �ɐ��������ɓ����͂̂荇�����A
�ɐ��������ɓ����͂̂荇�����A�@���A
 ......[��]
......[��]
 (b) �E�}���A��������Ƃ�����AA��
(b) �E�}���A��������Ƃ�����AA��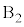 ��
��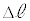 ���痣���܂ł̊Ԃ�A�̈ړ�����
���痣���܂ł̊Ԃ�A�̈ړ�����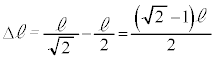 �́A�����������ɁA
�́A�����������ɁA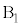 ......[��]�@����A
......[��]�@����A
(c) A��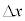 ���ڐG��ۂ��Ă���ԁA�E�}�̂悤��A��
���ڐG��ۂ��Ă���ԁA�E�}�̂悤��A��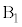 �~������ƁA
�~������ƁA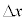 �͐���������
�͐���������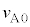 �����܂��B�܂�A���̊Ԃ�A�̑���
�����܂��B�܂�A���̊Ԃ�A�̑���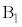 ��
��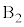 �C
�C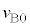 �̑���
�̑���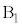 �͈�v���܂��B��������Ƃ�����AA��
�͈�v���܂��B��������Ƃ�����AA��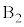 ��
��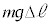 ���痣���܂ł̊Ԃ�A�̏����̈ʒu�G�l���M�[�̌�������
���痣���܂ł̊Ԃ�A�̏����̈ʒu�G�l���M�[�̌�������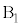 �ł��B��������Ƃ��ƁAA��
�ł��B��������Ƃ��ƁAA��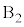 ��
��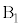 ���痣���Ƃ�(���̂Ƃ���A��
���痣���Ƃ�(���̂Ƃ���A��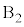 �C
�C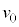 �̑�����
�̑�����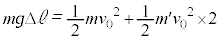 �Ƃ��܂�)�Ƃ��͊w�I�G�l���M�[�ۑ����A
�Ƃ��܂�)�Ƃ��͊w�I�G�l���M�[�ۑ����A �A���A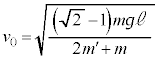
��  �@����BA��
�@����BA�� ��
��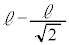 ���痣��Ă���A�����ɐڐG����܂ł�A���~�����鋗����
���痣��Ă���A�����ɐڐG����܂ł�A���~�����鋗���� �ł��BA��
�ł��BA�� ��
��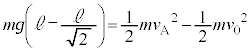 ���痣��Ă��܂��ƁA
���痣��Ă��܂��ƁA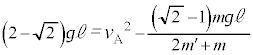 �C
�C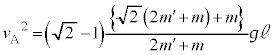 �͑���
�͑���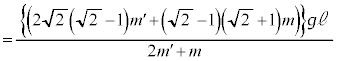 �œ����x�^�����܂��B����āAA�����ɐڐG���钼�O��
�œ����x�^�����܂��B����āAA�����ɐڐG���钼�O��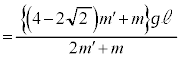 �C
�C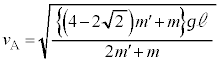 �̑�����
�̑�����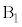 �ł��BA��
�ł��BA��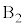 ��
��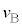 ���痣���Ƃ��ƁAA�����ɐڐG���钼�O�Ƃ̗͊w�I�G�l���M�[�ۑ����A
���痣���Ƃ��ƁAA�����ɐڐG���钼�O�Ƃ̗͊w�I�G�l���M�[�ۑ����A �B���A
�� 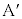 ......[��]
......[��]
A��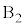 ��
��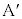 ���痣��Ĉȍ~B�͑���
���痣��Ĉȍ~B�͑���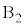 �œ����x�^������̂ŁA�B���A
�œ����x�^������̂ŁA�B���A 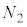 ......[��]
......[��]
[B]�@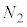 �̂Ƃ��A
�̂Ƃ��A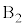 ��
��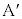 �̊Ԃ͊��炸�A
�̊Ԃ͊��炸�A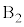 �ɂ́A���炩�łȂ��ʂɉ����ď�������Î~���C��F�������܂��B
�ɂ́A���炩�łȂ��ʂɉ����ď�������Î~���C��F�������܂��B 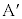 ��
��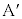 �ɋy�ڂ������R��(���炩�łȂ��ʂɐ�����
�ɋy�ڂ������R��(���炩�łȂ��ʂɐ�����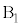 ����
����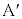 �Ɍ�������)�̑傫����
�Ɍ�������)�̑傫����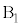 �Ƃ���ƁA��p����p�̖@�����A�����傫��
�Ƃ���ƁA��p����p�̖@�����A�����傫��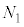 �ŋt����(���炩�łȂ��ʂɐ�����
�ŋt����(���炩�łȂ��ʂɐ�����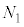 ����
����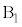 �Ɍ�������)�̐����R�͂�
�Ɍ�������)�̐����R�͂�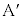 ����
����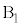 �ɓ����܂��B
�ɓ����܂��B
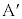 ��
��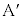 �ɋy�ڂ������R��(�ڐG�ʂɐ�����
�ɋy�ڂ������R��(�ڐG�ʂɐ�����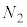 ����
����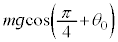 �Ɍ�������)�̑傫����
�Ɍ�������)�̑傫����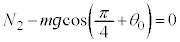 �Ƃ���ƁA��p����p�̖@�����A�����傫��
�Ƃ���ƁA��p����p�̖@�����A�����傫��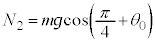 �ŋt����(�ڐG�ʂɐ�����
�ŋt����(�ڐG�ʂɐ�����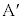 ����
����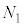 �Ɍ�������)�̐����R�͂�
�Ɍ�������)�̐����R�͂�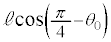 ����
����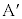 �ɓ����܂��B
�ɓ����܂��B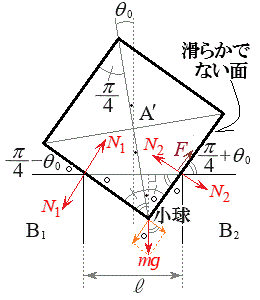 (d) �E�}���A���炩�łȂ��ʂɐ����ȕ�����
(d) �E�}���A���炩�łȂ��ʂɐ����ȕ�����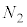 ����͂́A�����R��
����͂́A�����R��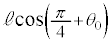 (�������)�Ə����ɓ����d�͂̂��̕����̐���
(�������)�Ə����ɓ����d�͂̂��̕����̐���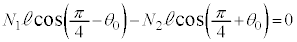 (�E������)�ł��B�����̗͂̂荇�����A
(�E������)�ł��B�����̗͂̂荇�����A
�� 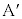 ......[��]�@����C
......[��]�@����C
(e) 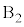 �������Č�����ς���Ƃ��A
�������Č�����ς���Ƃ��A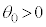 �͉�]�^�������܂��B
�͉�]�^�������܂��B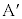 �̂Ƃ��ɂ�
�̂Ƃ��ɂ�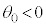 �͉�]�^�����܂���B�����ŁA
�͉�]�^�����܂���B�����ŁA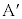 �ɓ����͂ɂ��āA�����̈ʒu�𒆐S�Ƃ����͂̃��[�����g���l���܂��B�E�}���A
�ɓ����͂ɂ��āA�����̈ʒu�𒆐S�Ƃ����͂̃��[�����g���l���܂��B�E�}���A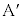 ���鐂���R��
���鐂���R��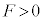 �̂��ł̒�����
�̂��ł̒�����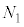 �ŁA���v���̃��[�����g�ł��B
�ŁA���v���̃��[�����g�ł��B 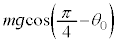 ���鐂���R��
���鐂���R��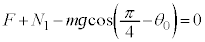 �̂��ł̒�����
�̂��ł̒�����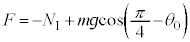 �ŁA�����v���̃��[�����g�ł��B
�ŁA�����v���̃��[�����g�ł��B
�͂̃��[�����g�̂荇�����A�� 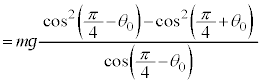 ......[��]�@����D
......[��]�@����D
(f) 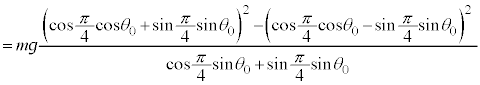 �̊��炩�łȂ��ʂ�
�̊��炩�łȂ��ʂ�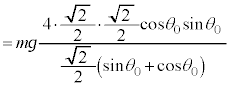 �̊Ԃɂ͖��C�͂������܂��B
�̊Ԃɂ͖��C�͂������܂��B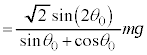 �ŏ�����
�ŏ�����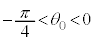 ���S��ʂ鉔���ʂ��E�ɂ���Ƃ��́A���C�͉͂E������A
���S��ʂ鉔���ʂ��E�ɂ���Ƃ��́A���C�͉͂E������A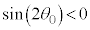 �ŏ�����
�ŏ�����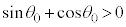 ���S��ʂ鉔���ʂ�荶�ɂ���Ƃ��́A���C�͍͂��������ł��B���炩�łȂ��ʂɉ���������
���S��ʂ鉔���ʂ�荶�ɂ���Ƃ��́A���C�͍͂��������ł��B���炩�łȂ��ʂɉ���������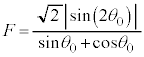 ����͂́A�Î~���C��F (
����͂́A�Î~���C��F (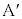 �̂Ƃ��E������Ƃ��܂�)�C�����R��
�̂Ƃ��E������Ƃ��܂�)�C�����R��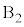 (�E�����)�C�����ɓ����d�͂̂��̕����̐���
(�E�����)�C�����ɓ����d�͂̂��̕����̐���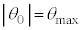 (��������)�ł��B�����̗͂̂荇�����A
(��������)�ł��B�����̗͂̂荇�����A �C�C�D���A
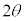 �ɂ����Ă�
�ɂ����Ă�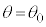 �C
�C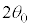 �ł���A��蕶�ł́AF�C�͂̑傫���Ƃ��Ă���̂ŁA
�ł���A��蕶�ł́AF�C�͂̑傫���Ƃ��Ă���̂ŁA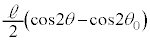 ......[��]
......[��]
(g) 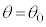 ��
��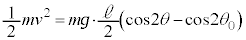 �̊Ԃ�����o���Ƃ��A�܂�A
�̊Ԃ�����o���Ƃ��A�܂�A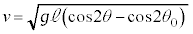 �ƂȂ�A�Î~���C��F���ő�Î~���C��
�ƂȂ�A�Î~���C��F���ő�Î~���C��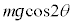 �ɓ������Ȃ�Ƃ��A�C���A
�ɓ������Ȃ�Ƃ��A�C���A 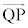 ......[��]
......[��]
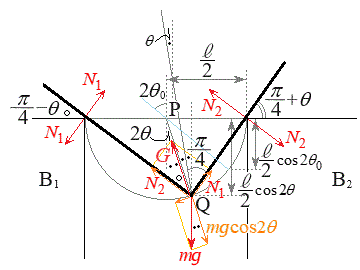 [C]�@�}4������ƁA�_P�𒆐S�Ƃ��ĒP�U��q�Ɠ����^�������鏬���̐U��q�̒�����
[C]�@�}4������ƁA�_P�𒆐S�Ƃ��ĒP�U��q�Ɠ����^�������鏬���̐U��q�̒�����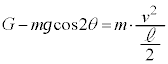 �ł�(��蕶�Ɂu�P�U��q�v�Ə�����Ă��܂����Aθ�����Ƃ����L�q���Ȃ��̂ŁA�����̉^���͒P�U���ł͂Ȃ��A�������s�����~�^���Ƃ��čl���܂�)�B�����̈ʒu��Q�Ƃ��āAPQ���������ƂȂ��p�́A��蕶�A�}4�ɂ���
�ł�(��蕶�Ɂu�P�U��q�v�Ə�����Ă��܂����Aθ�����Ƃ����L�q���Ȃ��̂ŁA�����̉^���͒P�U���ł͂Ȃ��A�������s�����~�^���Ƃ��čl���܂�)�B�����̈ʒu��Q�Ƃ��āAPQ���������ƂȂ��p�́A��蕶�A�}4�ɂ���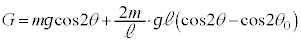 �ł��B���߂�A���u���ꂽ�Ƃ�(
�ł��B���߂�A���u���ꂽ�Ƃ�(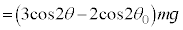 )�ɂ́APQ�Ɖ������Ƃ̂Ȃ��p��
)�ɂ́APQ�Ɖ������Ƃ̂Ȃ��p��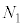 �ŁA�E�}���A���ʒu�ł̍����̍���
�ŁA�E�}���A���ʒu�ł̍����̍���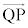 �ł��B
�ł��B
(h) 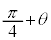 �̂Ƃ��ɂ́A�^���G�l���M�[��0�������̂ŁA�͊w�I�G�l���M�[�ۑ����A
�̂Ƃ��ɂ́A�^���G�l���M�[��0�������̂ŁA�͊w�I�G�l���M�[�ۑ����A �� 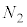 ......[��]�@����E
......[��]�@����E
�����ɓ����d�͂�PQ����������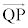 (�����͉�����)�ł��B
(�����͉�����)�ł��B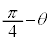 ��A�ɋy�ڂ������R��
��A�ɋy�ڂ������R��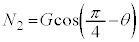 �C
�C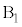 ��A�ɋy�ڂ������R��
��A�ɋy�ڂ������R��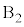 �̍���(��蕶�ɂ͉���������Ă��܂��A�P�U��q�̎��̕���
�̍���(��蕶�ɂ͉���������Ă��܂��A�P�U��q�̎��̕���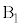 �����������Ƃ��čl���܂�)�̑傫����G�Ƃ��āA������
�����������Ƃ��čl���܂�)�̑傫����G�Ƃ��āA������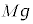 �������^���������́A
�������^���������́A 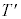
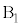 �@(�� �E)
�@(�� �E)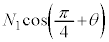 ......[��]�@����F
......[��]�@����F�����R��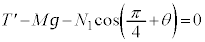 ��A�̍����ʂɐ����ʼnE���ʂɕ��s�ł��B
��A�̍����ʂɐ����ʼnE���ʂɕ��s�ł��B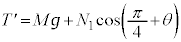 �ƉE���ʂ̂Ȃ��p�́A�E�}���
�ƉE���ʂ̂Ȃ��p�́A�E�}���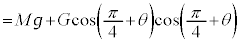 �ł��B����āA
�ł��B����āA 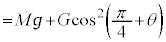 �@����G
�@����G�����R��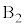 ��A�̉E���ʂɐ����ō����ʂɕ��s�ł��B
��A�̉E���ʂɐ����ō����ʂɕ��s�ł��B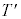 �ƍ����ʂ̂Ȃ��p�́A�E�}���
�ƍ����ʂ̂Ȃ��p�́A�E�}���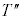 �ł��B����āA
�ł��B����āA 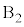 �@����H
�@����H
(i) 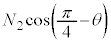 �C
�C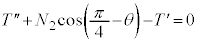 �͐Î~���Ă���̂ŁA�͂̂荇�����������Ă��܂��B
�͐Î~���Ă���̂ŁA�͂̂荇�����������Ă��܂��B 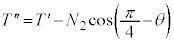 �ɐ��������ɓ����͂́A�����̎��̒���
�ɐ��������ɓ����͂́A�����̎��̒���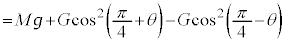 �C�E���̎��̒���
�C�E���̎��̒���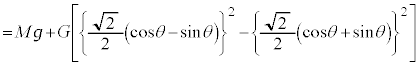 �CA��
�CA��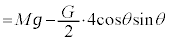 �ɋy�ڂ������R�͂̐�������
�ɋy�ڂ������R�͂̐�������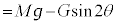 (������)�ł��B�����̗͂̂荇�����A
(������)�ł��B�����̗͂̂荇�����A�G���A
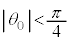
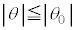 ......[��]�@����I
......[��]�@����I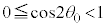 �ɐ��������ɓ����͂́A�����̎��̒���
�ɐ��������ɓ����͂́A�����̎��̒���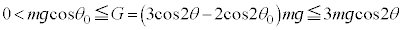 �C�E���̎��̒���
�C�E���̎��̒���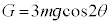 �CA��
�CA��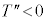 �ɋy�ڂ������R�͂̐�������
�ɋy�ڂ������R�͂̐�������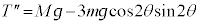 (�E����)�ł��B�����̗͂̂荇�����A
(�E����)�ł��B�����̗͂̂荇�����A�H�C�I���A
(j) 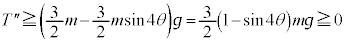 ��
��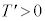 �̗����܂��͂����ꂩ�������Ƃ��A
�̗����܂��͂����ꂩ�������Ƃ��A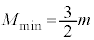 �C
�C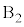 �Ɋւ���͂̂荇��������A�I�C�J���������Ȃ��Ȃ�܂��B
�Ɋւ���͂̂荇��������A�I�C�J���������Ȃ��Ȃ�܂��B �F�ɂ��ƁA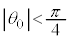 �͈̔͂ɂ����āA
�͈̔͂ɂ����āA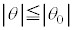 �C
�C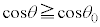 �C
�C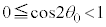 �Ȃ̂ŁA
�Ȃ̂ŁA �ł��BG���傫���Ȃ�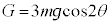 �ɂȂ�ƁA
�ɂȂ�ƁA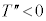 �ƂȂ�荇���������\�����o�Ă��܂����A���̂Ƃ��A
�ƂȂ�荇���������\�����o�Ă��܂����A���̂Ƃ��A 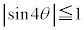 �ł����A
�ł����A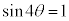 �ł����Ă�
�ł����Ă�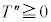 �ł��邽�߂�
�ł��邽�߂�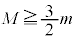 ���K�v�ŁA
���K�v�ŁA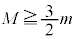 �ł���A
�ł���A�ł���A�͂̂荇���J�͈ێ�����܂��B���̂Ƃ��A�I�ɂ�����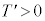 �ł����āA�͂̂荇���I���ێ�����܂��B����āA
�ł����āA�͂̂荇���I���ێ�����܂��B����āA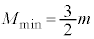 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 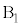 ......[��]�@����A
......[��]�@����A
 �@����B
�@����B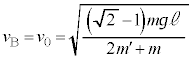
 ......[��]
......[��] ......[��]
......[��]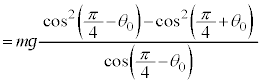 ......[��]�@����D
......[��]�@����D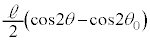 ......[��]
......[��]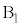
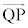 ......[��]
......[��]