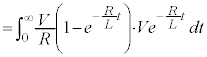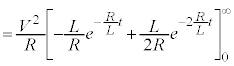�R�C���̉ߓn���ۂ̌v�Z�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
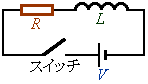 �E�}�̂悤�ɁA�N�d��V�̓d�r����RR�����ȃC���_�N�^���XL���R�C���ƃX�C�b�`��ڑ�������H���l���܂��B�ŏ��ɃX�C�b�`�͊J���Ă���Ƃ��܂��B
�E�}�̂悤�ɁA�N�d��V�̓d�r����RR�����ȃC���_�N�^���XL���R�C���ƃX�C�b�`��ڑ�������H���l���܂��B�ŏ��ɃX�C�b�`�͊J���Ă���Ƃ��܂��B
���� �ɂ����ăX�C�b�`����܂��B��H�ɗ�����d����I�Ƃ���ƁA��R�ɂ������d���~����
�ɂ����ăX�C�b�`����܂��B��H�ɗ�����d����I�Ƃ���ƁA��R�ɂ������d���~����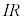 �C�R�C���ɂ������d���~����
�C�R�C���ɂ������d���~����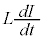 (���ȗU�����Q��)�C�L���q�z�b�t��2�@�����A
(���ȗU�����Q��)�C�L���q�z�b�t��2�@�����A
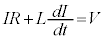 �@����@
�@����@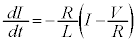
 �@(�������������Q��)
�@(�������������Q��)
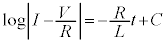 (C�F�ϕ��萔)��
(C�F�ϕ��萔)�� 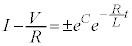 �͂��߂ɃR�C�����d����0�������̂ŁA
�͂��߂ɃR�C�����d����0�������̂ŁA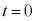 �ɂ�����
�ɂ�����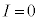 �Ƃ���ƁA
�Ƃ���ƁA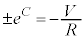
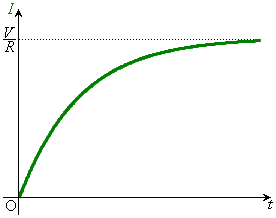 ��
�� 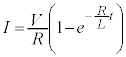
��H�𗬂���d���̕ω��̏��E�}�Ɏ����܂��B
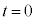 �̂Ƃ��A
�̂Ƃ��A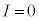 �ł����A����́A�R�C�����Œf������R������ɂȂ����̂Ɠ��l�̏ł��B�X�C�b�`��������ɃR�C���͒f�����Ă��܂����̂Ɠ��l�̓�������܂��B
�ł����A����́A�R�C�����Œf������R������ɂȂ����̂Ɠ��l�̏ł��B�X�C�b�`��������ɃR�C���͒f�����Ă��܂����̂Ɠ��l�̓�������܂��B
�܂��A�[�����Ԃ��o�����āA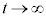 �Ƃ���ƁA
�Ƃ���ƁA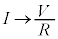 �ƂȂ�A�R�C������R�[���̓����Œu���������̂Ɠ��l�̏ɂȂ�܂��B���̂Ƃ��A
�ƂȂ�A�R�C������R�[���̓����Œu���������̂Ɠ��l�̏ɂȂ�܂��B���̂Ƃ��A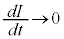 �Ȃ̂ŁA�R�C�����t�N�d���A�d���~�����[���ɂȂ�܂��B
�Ȃ̂ŁA�R�C�����t�N�d���A�d���~�����[���ɂȂ�܂��B
�����ŁA�R�C�������߂����G�l���M�[���l���Ă݂܂�(�d�����Q��)�B
�@���̗��ӂ��d��I��������ƁA
���̎��̉E�ӂ́A�d�r�����������d��(�d����)������R�ŏ������d��(�d����)�����������̂ł��B���ꂪ�A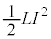 �̎��ԕω����ɓ������Ƃ������Ƃ́A�d�r�����������d��������R�ŏ������W���[���M�����������̂́A
�̎��ԕω����ɓ������Ƃ������Ƃ́A�d�r�����������d��������R�ŏ������W���[���M�����������̂́A �Ƃ����`�ŃR�C���Ɏc���Ă��邱�Ƃł����āA
�Ƃ����`�ŃR�C���Ɏc���Ă��邱�Ƃł����āA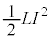 �̓R�C�������߂����G�l���M�[��\���܂��B
�̓R�C�������߂����G�l���M�[��\���܂��B
���ۂɁA�E�ӂ�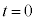 ����
����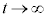 �܂Őϕ�����ƁA
�܂Őϕ�����ƁA
�ƂȂ��āA�[�����������o�߂����Ƃ��� �̒l�Ɉ�v���܂��B
�̒l�Ɉ�v���܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B