東京大学2013年前期物理入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] 次のⅠ,Ⅱの各問に答えよ。
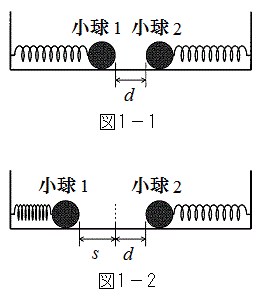 Ⅰ 図1-1のように、なめらかな水平面上で、ばね定数がkのばね2本を向かい合わせに、それぞれ左側および右側の壁に一端を固定し、他方の端に同じ質量mの小球1および小球2をそれぞれ取り付けた。ばねが自然長のとき、小球間の距離はdであった。ただし、小球の大きさとばねの質量は無視してよい。
Ⅰ 図1-1のように、なめらかな水平面上で、ばね定数がkのばね2本を向かい合わせに、それぞれ左側および右側の壁に一端を固定し、他方の端に同じ質量mの小球1および小球2をそれぞれ取り付けた。ばねが自然長のとき、小球間の距離はdであった。ただし、小球の大きさとばねの質量は無視してよい。今、図1-2のように、小球1を、ばねが自然長になる位置から、ばねが縮む方向に距離sだけ動かし(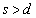 )、そこで静かに放した。以下の設問に答えよ。
)、そこで静かに放した。以下の設問に答えよ。 (1) 小球1は動き始め小球2に衝突した。衝突直前の小球1の速さを求めよ。
(2) 小球どうしの衝突は弾性衝突であるとして、この衝突直後の小球1と小球2の速さをそれぞれ求めよ。
(3) この衝突後、再び衝突するまでに、小球1側のばねおよび小球2側のばねは、それぞれ自然長から最大どれだけ縮むか答えよ。
(4) 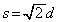 の場合に、最初の衝突から再衝突までの時間を求めよ。
の場合に、最初の衝突から再衝突までの時間を求めよ。 Ⅱ 次に、あらい水平面上に、Ⅰと同じばねと小球を用意した場合を考える。どちらの小球も水平面との間の静止摩擦係数はμ,動摩擦係数は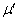 である。重力加速度の大きさをgとして以下の設問に答えよ。
である。重力加速度の大きさをgとして以下の設問に答えよ。 (1) Ⅰと同じように(図1-2)、小球1を、ばねが自然長になる位置から、ばねが縮む方向に距離sだけ動かし、そこで静かに放した。小球1が動き始めるために、sがみたすべき条件を求めよ。
(2) 小球1が動き始めた後、小球2に衝突するためにsがとるべき最小値を求めよ。 [解答へ]
 [2] 電荷をもった粒子の運動を磁場により制御することを考える。重力の効果は無視できるものとして、以下の設問に答えよ。ただし、角度の単位はすべてラジアンとする。また、θ を微小な角度とするとき、
[2] 電荷をもった粒子の運動を磁場により制御することを考える。重力の効果は無視できるものとして、以下の設問に答えよ。ただし、角度の単位はすべてラジアンとする。また、θ を微小な角度とするとき、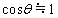 ,
,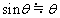 ,
,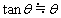 と近似してよい。
と近似してよい。
Ⅰ 図2-1のように、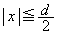 の領域
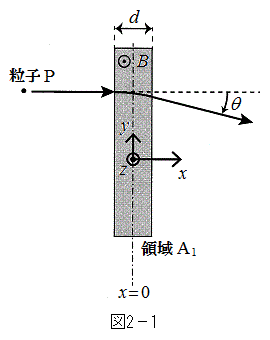
の領域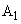 にのみ、磁束密度がy座標にゆるやかに依存する磁場がz軸方向(紙面に垂直、手前向きを正)にかけられている。質量m,正の電荷qをもつ粒子Pを、x軸正方向に速さvで領域
にのみ、磁束密度がy座標にゆるやかに依存する磁場がz軸方向(紙面に垂直、手前向きを正)にかけられている。質量m,正の電荷qをもつ粒子Pを、x軸正方向に速さvで領域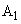 に入射する。
に入射する。 (1) 領域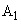 を通過した結果、粒子Pの運動方向が微小な角度だけ曲がり、そのx軸からの角度がθ となった。領域
を通過した結果、粒子Pの運動方向が微小な角度だけ曲がり、そのx軸からの角度がθ となった。領域 内を通過する間、粒子のy座標の変化は小さく、粒子に働く磁束密度Bはその間一定としてよいとする。このときのθ を求めよ。以後、角度の向きは図2-1の矢印の向きを正とする。
内を通過する間、粒子のy座標の変化は小さく、粒子に働く磁束密度Bはその間一定としてよいとする。このときのθ を求めよ。以後、角度の向きは図2-1の矢印の向きを正とする。 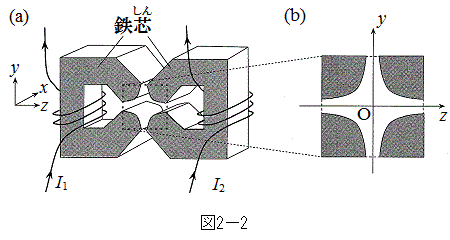 (3) 図2-2(a)のように配置された電磁石の組の点線で囲まれた範囲(拡大図と座標を図2-2(b)に示す)を考える。鉄芯(しん)を適切な形に制作すると、
(3) 図2-2(a)のように配置された電磁石の組の点線で囲まれた範囲(拡大図と座標を図2-2(b)に示す)を考える。鉄芯(しん)を適切な形に制作すると、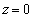 の平面内で(2)のような磁場が実現できる。このとき、二つの電磁石に流す電流
の平面内で(2)のような磁場が実現できる。このとき、二つの電磁石に流す電流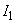 ,
,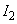 の向きはどうするべきか。それぞの符号を答えよ。ただし、図中の矢印の向きを正とする。
の向きはどうするべきか。それぞの符号を答えよ。ただし、図中の矢印の向きを正とする。
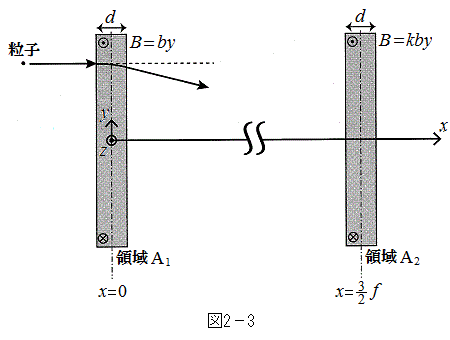 Ⅱ 次に、Ⅰ(2)の領域に加えて、図2-3のように、
Ⅱ 次に、Ⅰ(2)の領域に加えて、図2-3のように、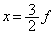 を中心とし幅dの範囲に、z軸方向に磁束密度
を中心とし幅dの範囲に、z軸方向に磁束密度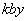 (kは定数)の磁場がかかっている領域
(kは定数)の磁場がかかっている領域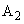 を考える。ここで、領域
を考える。ここで、領域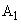 と
と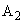 を両方通過した後の粒子の運動方向の変化は、それぞれの領域でⅠ(1)のように求めた曲げ角の和として計算できるものとし、またdはf に比べて無視できるほど小さいとしてよいとする。粒子Pと、同じ電荷qをもつ別の粒子Qとが、x軸正方向に速さvをもって
を両方通過した後の粒子の運動方向の変化は、それぞれの領域でⅠ(1)のように求めた曲げ角の和として計算できるものとし、またdはf に比べて無視できるほど小さいとしてよいとする。粒子Pと、同じ電荷qをもつ別の粒子Qとが、x軸正方向に速さvをもって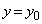 で領域
で領域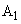 に別個に入射したところ、粒子Pの運動方向が微小な角度
に別個に入射したところ、粒子Pの運動方向が微小な角度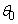 ,粒子Qの運動方向が角度
,粒子Qの運動方向が角度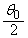 だけ曲げられて、それぞれ領域
だけ曲げられて、それぞれ領域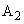 に入射した。
に入射した。(1) 粒子Qの質量を求めよ。
(2) 粒子P,粒子Qが領域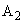 に入る際のy座標は、それぞれ
に入る際のy座標は、それぞれ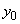 の何倍となるか。
の何倍となるか。 (3) 粒子P,粒子Qが領域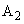 を通過した後の運動方向のx軸からの角度を、それぞれkと
を通過した後の運動方向のx軸からの角度を、それぞれkと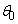 を用いて表せ。
を用いて表せ。 (4) kの値を調整すると、粒子Pと粒子Qが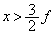 でx軸上のの同じ点を通過するようにできる。このときのkの値を求めよ。
でx軸上のの同じ点を通過するようにできる。このときのkの値を求めよ。 [解答へ]
[3] 次のⅠ,Ⅱ,Ⅲの各問に答えよ。なお、角度の単位はラジアンとする。
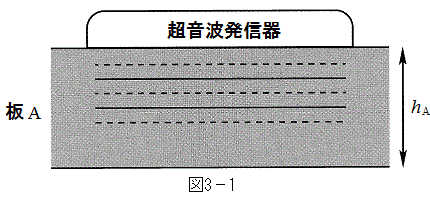 Ⅰ 図3-1のように、超音波発信器を用いて平面波に近い超音波を板Aに入射する(板中の直線は波面を表す)。振動数を変化させながら縦波の超音波を板面に垂直に入射したところ、振動数が
Ⅰ 図3-1のように、超音波発信器を用いて平面波に近い超音波を板Aに入射する(板中の直線は波面を表す)。振動数を変化させながら縦波の超音波を板面に垂直に入射したところ、振動数が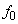 の整数倍になるごとに板が共振した。板Aの厚さを
の整数倍になるごとに板が共振した。板Aの厚さを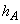 ,板A内を伝わる縦波の超音波の速さを
,板A内を伝わる縦波の超音波の速さを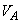 とする。また、板の両面は自由端とする。
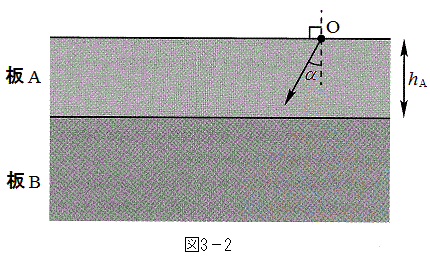
とする。また、板の両面は自由端とする。(2) 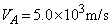 のとき、振動数
のとき、振動数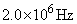 と
と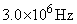 の両方で共振が起こった。
の両方で共振が起こった。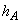 の最小値を求めよ。
の最小値を求めよ。
 Ⅱ 固体中では縦波と横波の両方が存在する。縦波と横波は速さが異なり、縦波の方がk倍(
Ⅱ 固体中では縦波と横波の両方が存在する。縦波と横波は速さが異なり、縦波の方がk倍(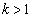 )速い。図3-2のように板Aと、それとは材質の異なる板Bを貼り合わせ、2層構造を持つ板を作製した。板B内を伝わる縦波の速さを
)速い。図3-2のように板Aと、それとは材質の異なる板Bを貼り合わせ、2層構造を持つ板を作製した。板B内を伝わる縦波の速さを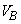 とし、
とし、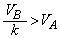 とする。また、kの値は物質の種類によらないとする。
とする。また、kの値は物質の種類によらないとする。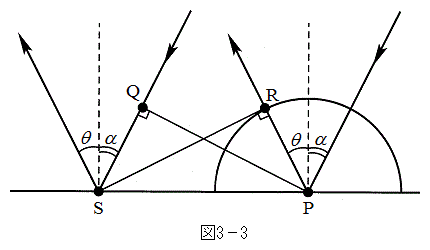 (1) 縦波の反射角θ が入射角αと等しくなることをホイヘンスの原理に基づいて考える。図3-3中の記号P,Q,R,Sを用いて、 を埋めよ。
(1) 縦波の反射角θ が入射角αと等しくなることをホイヘンスの原理に基づいて考える。図3-3中の記号P,Q,R,Sを用いて、 を埋めよ。