������w2022�N�O�������������
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
[1]�@�n���\�ʏ�̊C���́A�n������̖��L���͂̑��ɁA���⑾�z����̈��́A����ɒn���⌎�̉^���ɂ���Ĉ����N�������l�X�ȗ͂���B�����̗͂̈ꕔ�����ԂƂƂ��ɕω����邱�ƂŁA���̖��������N����(�����^��)�B�����ł́A�n���̕\�ʂɒu���ꂽ���̂ɓ����͂ɂ��āA�P�����������f���ōl�@���悤�B�Ȃ��A���L���͒萔��G�Ƃ��A�n���͎���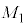 �Ŗ��x����l�Ȕ��aR�̋��̂Ƃ݂Ȃ���Ƃ���B�ȉ��̐ݖ�T�C�U�C�V�ɓ�����B
�Ŗ��x����l�Ȕ��aR�̋��̂Ƃ݂Ȃ���Ƃ���B�ȉ��̐ݖ�T�C�U�C�V�ɓ�����B
�T�@�n���̕\�ʂɒu���ꂽ���̂͒n���̎��]�ɂ�鉓�S�͂���B�n���̎��]������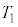 �Ƃ���Ƃ��A�ȉ��̐ݖ�ɓ�����B
�Ƃ���Ƃ��A�ȉ��̐ݖ�ɓ�����B
(1) ����m�̎��_���ԓ���̂���n�_E�ɒu���ꂽ�Ƃ��ɓ������S�͂̑傫��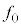 �C����іk��
�C����іk��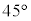 �̂���n�_F�ɒu���ꂽ�Ƃ��ɓ������S�͂̑傫��
�̂���n�_F�ɒu���ꂽ�Ƃ��ɓ������S�͂̑傫��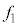 �����߁A���ꂼ��m�CR�C
�����߁A���ꂼ��m�CR�C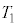 ��p���ĕ\���B
��p���ĕ\���B
(2) �ݖ�T(1)�̒n�_E�ɂ�����A�n���̎��]�ɂ�鉓�S�͂̌��ʂ��܂߂��d�͉����x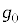 �����߁AG�C
�����߁AG�C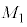 �CR�C
�CR�C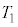 ��p���ĕ\���B
��p���ĕ\���B
 �U�@���ɁA������̈��͂ƁA�����n���̎�������]�^�����邱�Ƃɂ���Ĕ�������͂��l����B�����ł͂����̗͂ɂ��Ă̂ݍl���邽�߁A�n�������]���Ȃ��Ƃ������z�I�ȏꍇ�ɂ��čl�@����B
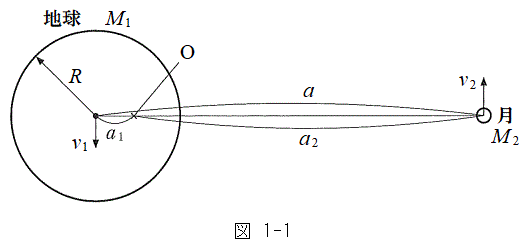
�U�@���ɁA������̈��͂ƁA�����n���̎�������]�^�����邱�Ƃɂ���Ĕ�������͂��l����B�����ł͂����̗͂ɂ��Ă̂ݍl���邽�߁A�n�������]���Ȃ��Ƃ������z�I�ȏꍇ�ɂ��čl�@����B�����n���̎�������]����Ƃ��A�n���ƌ��́A�n���ƌ��̏d�S�ł���_O�𒆐S�ɓ�������ʼn~�^������Ɖ��肷��(�}1-1)�B�Ȃ��A�}1-1�ɂ����āA���̉~�^���̉�]���͎��ʂɐ����ł���B���͎���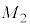 �̎��_�Ƃ��A�n���̒��S�ƌ��Ƃ̋�����a�Ƃ���B�܂��A�n���̒��S����ь�����_O�܂ł̋��������ꂼ��
�̎��_�Ƃ��A�n���̒��S�ƌ��Ƃ̋�����a�Ƃ���B�܂��A�n���̒��S����ь�����_O�܂ł̋��������ꂼ�� �C
�C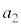 �Ƃ���B�ȉ��̐ݖ�ɓ�����B
�Ƃ���B�ȉ��̐ݖ�ɓ�����B
(1) �_O���猩���n���̒��S����ь��̑��������ꂼ��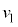 �C
�C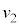 �Ƃ���B
�Ƃ���B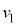 �����
�����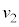 ��a�CG�C
��a�CG�C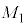 �C
�C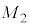 ��p���ĕ\���B
��p���ĕ\���B 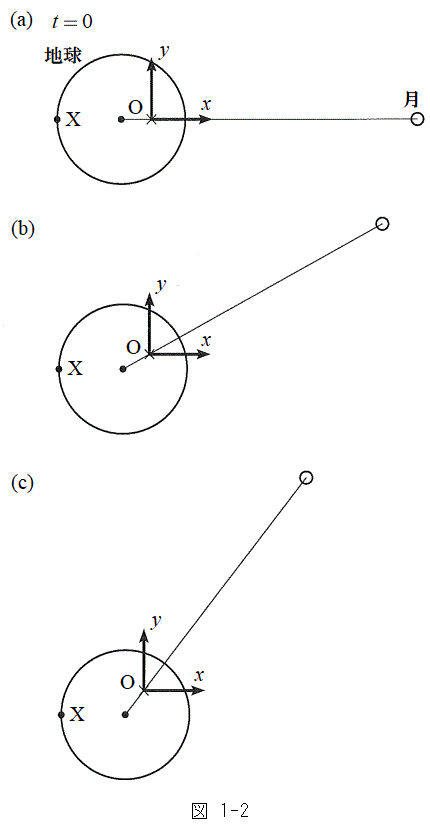 (2) �_O�����_�Ƃ��ČŒ肵��xy���W�n���A�}1-2(a)�̂悤�Ɏ��ʂƓ��ꕽ�ʂɂƂ�B����
(2) �_O�����_�Ƃ��ČŒ肵��xy���W�n���A�}1-2(a)�̂悤�Ɏ��ʂƓ��ꕽ�ʂɂƂ�B����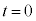 �ɂ����āA���W��
�ɂ����āA���W��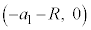 �ł���n���\�ʏ�̓_��_X�Ƃ���B���̌��]������
�ł���n���\�ʏ�̓_��_X�Ƃ���B���̌��]������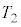 �Ƃ���Ƃ��A����t �ɂ�����_X�̍��W���A
�Ƃ���Ƃ��A����t �ɂ�����_X�̍��W���A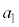 �CR�C
�CR�C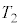 �Ct ��p���ĕ\���B�������A�n���̎��]�����Ă��邽�߁A����
�Ct ��p���ĕ\���B�������A�n���̎��]�����Ă��邽�߁A����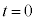 �ȍ~�Ő}1-2(b)�C(c)�̂悤�Ɉʒu�W���ω����邱�Ƃɒ��ӂ���B
�ȍ~�Ő}1-2(b)�C(c)�̂悤�Ɉʒu�W���ω����邱�Ƃɒ��ӂ���B
(3) �ݖ�U(2)�̓_X�ɁA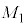 �����
�����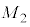 �ɔ䂵�ď\���ɏ���������m�̎��_���u����Ă���Ƃ����l����B���̎��_�ɂ��āA�n�����_O�𒆐S�Ƃ����~�^�������邱�ƂŐ����鉓�S�͂̑傫��
�ɔ䂵�ď\���ɏ���������m�̎��_���u����Ă���Ƃ����l����B���̎��_�ɂ��āA�n�����_O�𒆐S�Ƃ����~�^�������邱�ƂŐ����鉓�S�͂̑傫��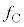 �����߁AG�Cm�C
�����߁AG�Cm�C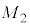 �Ca��p���ĕ\���B
�Ca��p���ĕ\���B
(4) ���鎞���ɂ����āA�n���\�ʏ�Ō�����ł������_��P�C���ɍł��߂��_��Q�Ƃ���B����m�̎��_��_P����ѓ_Q�ɒu�����ꍇ�ɁA���_�ɓ������S�͂ƌ�����̖��L���͂̍��͂̑傫�������ꂼ��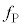 �C
�C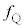 �Ƃ���B
�Ƃ���B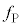 �C
�C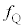 ��G�Cm�C
��G�Cm�C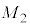 �Ca�CR��p���ĕ\���B�܂��A�_P����ѓ_Q�ɂ����鍇�͂̌����͌����牓������������A�߂Â������������ꂼ�ꓚ����B
�Ca�CR��p���ĕ\���B�܂��A�_P����ѓ_Q�ɂ����鍇�͂̌����͌����牓������������A�߂Â������������ꂼ�ꓚ����B
�V�@����ɁA���z����̈��͂ƁA�n���̌��]�^���ɂ���Ĕ�������͂ɂ��čl����B�����̗͂ɂ��Ă��ݖ�U�Ɠ��l�ɍl��������̂Ƃ���B�Ȃ��A�n���Ƒ��z�̏d�S��_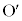 �Ƃ���B���z�͎���
�Ƃ���B���z�͎���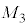 �̎��_�Ƃ��A�n���̒��S�Ƒ��z�̋�����b�Ƃ���B
�̎��_�Ƃ��A�n���̒��S�Ƒ��z�̋�����b�Ƃ���B 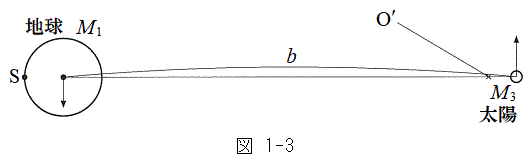 �}1-3�̂悤�ɁA���鎞���ɂ����Ēn���\�ʏ�ő��z����ł������_��S�Ƃ���B����m�̎��_���_S�ɒu���ꂽ�Ƃ��A�n�����_
�}1-3�̂悤�ɁA���鎞���ɂ����Ēn���\�ʏ�ő��z����ł������_��S�Ƃ���B����m�̎��_���_S�ɒu���ꂽ�Ƃ��A�n�����_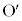 �𒆐S�Ƃ����~�^�������邱�ƂŐ����鉓�S�͂Ƒ��z����̖��L���͂̍��͂̑傫����
�𒆐S�Ƃ����~�^�������邱�ƂŐ����鉓�S�͂Ƒ��z����̖��L���͂̍��͂̑傫����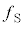 �Ƃ���B�ݖ�U(4)�ŋ��߂�
�Ƃ���B�ݖ�U(4)�ŋ��߂�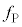 �ɑ���
�ɑ���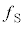 �̔�͈ȉ��̂悤�Ɍ��ς��邱�Ƃ��ł���B
�̔�͈ȉ��̂悤�Ɍ��ς��邱�Ƃ��ł���B�\1-1
| �n���̎��� | 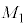 | 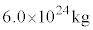 |
| ���̎��� | 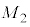 | 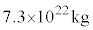 |
| ���z�̎��� | 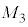 | 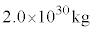 |
| �n���̒��S�ƌ��Ƃ̋��� | a | 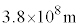 |
| �n���̒��S�Ƒ��z�Ƃ̋��� | b | 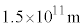 |
| �n���̔��a | R | 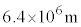 |
| ���L���͒萔 | G | 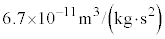 |
[��]
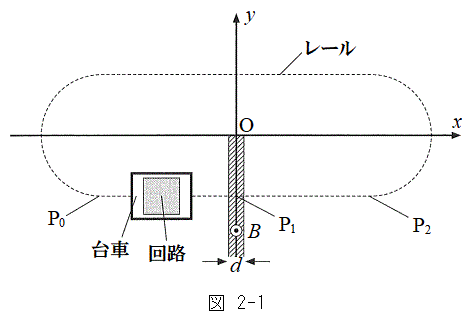 [2]�@�}2-1�̂悤�ɁA������xy���ʏ�Ɍ��_O�𒆐S�Ƃ������~�`�̃��[��������A�ΐ��Ŏ����ꂽ
[2]�@�}2-1�̂悤�ɁA������xy���ʏ�Ɍ��_O�𒆐S�Ƃ������~�`�̃��[��������A�ΐ��Ŏ����ꂽ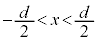 �C
�C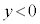 �̗̈�ɂ͉�������������Ɏ������x�̑傫����B�̈�l�Ȏ��ꂪ�������Ă���B���[����ɖؐ��̑�Ԃ�����A�R�C�����܂މ�H����ԂɌŒ肳��Ă���B�R�C����xy���ʂɕ��s�Ȑ����`�ŁA��ӂ̒�����L�C�������A
�̗̈�ɂ͉�������������Ɏ������x�̑傫����B�̈�l�Ȏ��ꂪ�������Ă���B���[����ɖؐ��̑�Ԃ�����A�R�C�����܂މ�H����ԂɌŒ肳��Ă���B�R�C����xy���ʂɕ��s�Ȑ����`�ŁA��ӂ̒�����L�C�������A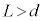 �Ƃ���B�R�C���̎l�̕ӂ͑�Ԃ̐i�s�����ɑ��ĕ��s�܂��͐����ł���B�ォ�猩���Ƃ���ԂƃR�C���̒��S�͈�v���Ă���A��H���܂ޑ�Ԃ̎��ʂ�m�ł���B���[���̒�����
�Ƃ���B�R�C���̎l�̕ӂ͑�Ԃ̐i�s�����ɑ��ĕ��s�܂��͐����ł���B�ォ�猩���Ƃ���ԂƃR�C���̒��S�͈�v���Ă���A��H���܂ޑ�Ԃ̎��ʂ�m�ł���B���[���̒�����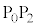 �͑�Ԃ̑傫���ɔ�ׂď\���������̂Ƃ��A���
�͑�Ԃ̑傫���ɔ�ׂď\���������̂Ƃ��A���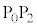 ���
���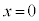 �̓_��
�̓_��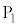 �Ƃ���B
�Ƃ���B
��Ԃ��_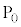 �𑬂�
�𑬂�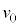 ��x���̐��̕���(�}�̉E����)�ɏo�����A���̌�A��Ԃ̒��S���ŏ���
��x���̐��̕���(�}�̉E����)�ɏo�����A���̌�A��Ԃ̒��S���ŏ���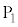 �C
�C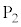 ��ʉ߂����u�Ԃ̑��������ꂼ��
��ʉ߂����u�Ԃ̑��������ꂼ��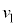 �C
�C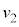 �Ƃ���B
�Ƃ���B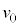 �ɔ�ׂđ����̕ω�
�ɔ�ׂđ����̕ω�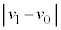 ��
��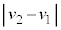 �͏\���ɏ������B�܂��A
�͏\���ɏ������B�܂��A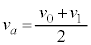 �Ƃ���B�R�C���̉E�ӂ�����ɐi������u�ԂƎ��ꂩ��o��u�Ԃ̑�Ԃ̒��S�ʒu�����ꂼ��
�Ƃ���B�R�C���̉E�ӂ�����ɐi������u�ԂƎ��ꂩ��o��u�Ԃ̑�Ԃ̒��S�ʒu�����ꂼ��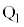 �C
�C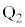 �Ƃ���B���l�ɁA���ӂ�����ɐi������u�ԂƏo��u�Ԃ̑�Ԃ̒��S�ʒu�����ꂼ��
�Ƃ���B���l�ɁA���ӂ�����ɐi������u�ԂƏo��u�Ԃ̑�Ԃ̒��S�ʒu�����ꂼ��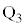 �C
�C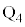 �Ƃ���B��Ԃɓ������C�͂��C��R�A�R�C�����g�̓d�C��R�͖����ł���B
�Ƃ���B��Ԃɓ������C�͂��C��R�A�R�C�����g�̓d�C��R�͖����ł���B
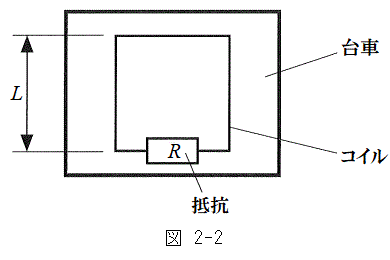 �T�@�}2-2�̂悤�ɁA��H�������`�̈ꊪ���R�C���ƒ�R�lR�̒�R����Ȃ�ꍇ�ɁA��Ԃ��ŏ��ɋ��
�T�@�}2-2�̂悤�ɁA��H�������`�̈ꊪ���R�C���ƒ�R�lR�̒�R����Ȃ�ꍇ�ɁA��Ԃ��ŏ��ɋ��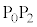 �𑖂鎞�̉^�����l����B
�𑖂鎞�̉^�����l����B
(1) ��Ԃ̒��S��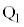 ����
����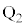 �ֈړ�����^���ɂ��āA�ȉ���
�ֈړ�����^���ɂ��āA�ȉ��� ��
�� �ɓ��鎮��
�ɓ��鎮��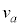 �CL�Cd�CB�Cm�CR�̂����K�v�Ȃ��̂�p���ĕ\���B�����̕����͉���������𐳂Ƃ���B
�CL�Cd�CB�Cm�CR�̂����K�v�Ȃ��̂�p���ĕ\���B�����̕����͉���������𐳂Ƃ���B �����ɔ�ׂđ����̕ω����\���ɏ��������߁A��Ԃ�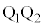 �Ԃ��ړ�����̂ɂ����鎞�Ԃ�
�Ԃ��ړ�����̂ɂ����鎞�Ԃ�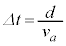 �Ƌߎ��ł���B�ړ��̑O��ł̃R�C����ʂ鎥���̕ω���
�Ƌߎ��ł���B�ړ��̑O��ł̃R�C����ʂ鎥���̕ω���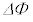 ��
�� �ł���A���̊Ԃ̗U���N�d�͂̕��ϒl��
�ł���A���̊Ԃ̗U���N�d�͂̕��ϒl��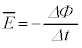 �Ə������Ƃ��ł���B�ړ����ɗU���N�d�͂�
�Ə������Ƃ��ł���B�ړ����ɗU���N�d�͂�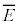 �ň��ł���Ƌߎ�����ƁA���̊Ԃɒ�R�Ŕ�������W���[���M�̑��a��
�ň��ł���Ƌߎ�����ƁA���̊Ԃɒ�R�Ŕ�������W���[���M�̑��a�� �Ə�����B
�Ə�����B
(2) 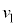 ��
��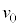 �CL�Cd�CB�Cm�CR�̂����K�v�Ȃ��̂�p���ĕ\���B
�CL�Cd�CB�Cm�CR�̂����K�v�Ȃ��̂�p���ĕ\���B
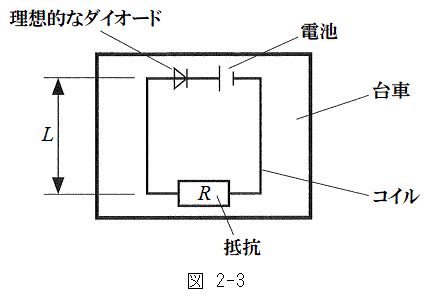 �U�@�����`�̈ꊪ���R�C���ɁA��R�lR�̒�R�A�N�d��V�œ�����R�̖����ł���d�r�A���z�I�ȃ_�C�I�[�h���ڑ����ꂽ��H���Ԃɍڂ��đ��点��B���z�I�ȃ_�C�I�[�h�Ƃ́A�������ɂ͒�R�Ȃ��ɓd����ʂ��A�t�����ɂ͓d���𗬂��Ȃ��f�q�ł���B�}2-3�́A���
�U�@�����`�̈ꊪ���R�C���ɁA��R�lR�̒�R�A�N�d��V�œ�����R�̖����ł���d�r�A���z�I�ȃ_�C�I�[�h���ڑ����ꂽ��H���Ԃɍڂ��đ��点��B���z�I�ȃ_�C�I�[�h�Ƃ́A�������ɂ͒�R�Ȃ��ɓd����ʂ��A�t�����ɂ͓d���𗬂��Ȃ��f�q�ł���B�}2-3�́A���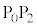 �𑖂��Ԃ��ォ�猩�����̂ł���B
�𑖂��Ԃ��ォ�猩�����̂ł���B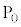 ���o��������Ԃ͎����ʉ߂��邱�Ƃɂ�茸�������B
���o��������Ԃ͎����ʉ߂��邱�Ƃɂ�茸�������B��Ԃ��ŏ��ɋ��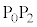 �𑖂鎞�̉^���ɂ��āA
�𑖂鎞�̉^���ɂ��āA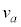 �CL�Cd�CB�Cm�CR�CV�̂����K�v�Ȃ��̂�p���Đݖ�(1)�`(3)�ɓ�����B�������A�ݖ�T�Ɠ��l�̋ߎ���p���邱�Ƃ��ł�����̂Ƃ���B
�CL�Cd�CB�Cm�CR�CV�̂����K�v�Ȃ��̂�p���Đݖ�(1)�`(3)�ɓ�����B�������A�ݖ�T�Ɠ��l�̋ߎ���p���邱�Ƃ��ł�����̂Ƃ���B
(1) ��Ԃ̒��S��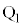 ����
����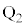 �ֈړ�����ԂɃR�C���ɗ����d���̑傫�������߂�B
�ֈړ�����ԂɃR�C���ɗ����d���̑傫�������߂�B
(2) ���̓d���ɂ��R�C�������ꂩ��郍�[�����c�͂����߂�B�͂̕����́Ax�����̌����𐳂Ƃ���B
(3) ���l�ɁA��Ԃ̒��S��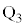 ����
����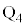 �ֈړ�����Ԃ̃��[�����c�͂����߂�B
�ֈړ�����Ԃ̃��[�����c�͂����߂�B ��Ԃ̓��[������J��Ԃ����Ȃ��珙�X�ɑ��x�������A�₪�Ĉ��̑���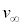 �ʼn^������悤�ɂȂ����B�ݖ�(4)�C(5)�ɓ�����B
�ʼn^������悤�ɂȂ����B�ݖ�(4)�C(5)�ɓ�����B 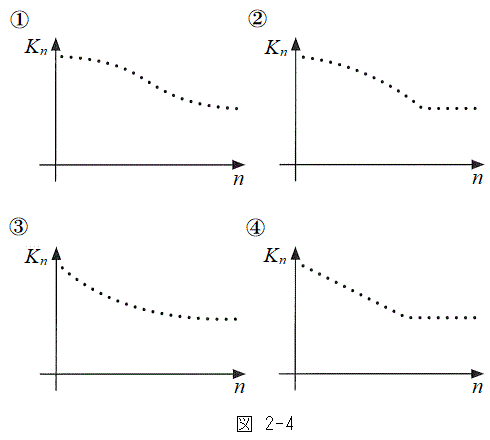 (4) n��ڂ�
(4) n��ڂ�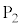 ��ʂ蔲�������̑�Ԃ̉^���G�l���M�[
��ʂ蔲�������̑�Ԃ̉^���G�l���M�[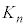 ��n�̊��Ƃ��ăO���t�ɕ`�����ꍇ�A�}2-4�̇@�`�C�̂ǂ̌`���ł��K��������B
��n�̊��Ƃ��ăO���t�ɕ`�����ꍇ�A�}2-4�̇@�`�C�̂ǂ̌`���ł��K��������B
(5) ����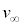 ��
��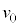 �CL�Cd�CB�Cm�CR�CV�̂����K�v�Ȃ��̂�p���ĕ\���B
�CL�Cd�CB�Cm�CR�CV�̂����K�v�Ȃ��̂�p���ĕ\���B
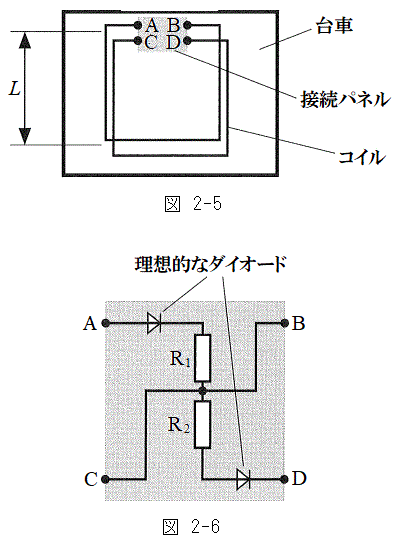 �V�@2�{�̐����`�ꊪ���R�C���Ɛڑ��p�l������Ȃ��H���Ԃɍڂ��đ��点��B�}2-5�͋��
�V�@2�{�̐����`�ꊪ���R�C���Ɛڑ��p�l������Ȃ��H���Ԃɍڂ��đ��点��B�}2-5�͋��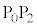 �𑖂��Ԃ��ォ�猩�����̂ł���B2�{�̃R�C���̗��[�͐ڑ��p�l���̒[�qA�CB�CC�CD�ɐڑ�����Ă���B�ڑ��p�l���͐}2-6�Ɏ����悤�Ȓ�R�Ɨ��z�I�ȃ_�C�I�[�h����Ȃ��H�ł���B�ݖ�T�Ɠ��l�̋ߎ���p���邱�Ƃ��ł�����̂Ƃ��A��Ԃ��ŏ��ɋ��
�𑖂��Ԃ��ォ�猩�����̂ł���B2�{�̃R�C���̗��[�͐ڑ��p�l���̒[�qA�CB�CC�CD�ɐڑ�����Ă���B�ڑ��p�l���͐}2-6�Ɏ����悤�Ȓ�R�Ɨ��z�I�ȃ_�C�I�[�h����Ȃ��H�ł���B�ݖ�T�Ɠ��l�̋ߎ���p���邱�Ƃ��ł�����̂Ƃ��A��Ԃ��ŏ��ɋ��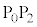 �𑖂鎞�̉^���ɂ��āA�ȉ��̐ݖ�ɓ�����B2�{�̃R�C���͏ォ�猩���Ƃ��Ɋ��S�ɏd�Ȃ��Ă���Ƃ݂Ȃ����Ƃ��ł��A�ڑ��p�l���ȊO�̕����ł݂͌��ɐ≏����Ă���B�܂��A�ڑ��p�l���̑傫���͖����ł�����̂Ƃ���B
�𑖂鎞�̉^���ɂ��āA�ȉ��̐ݖ�ɓ�����B2�{�̃R�C���͏ォ�猩���Ƃ��Ɋ��S�ɏd�Ȃ��Ă���Ƃ݂Ȃ����Ƃ��ł��A�ڑ��p�l���ȊO�̕����ł݂͌��ɐ≏����Ă���B�܂��A�ڑ��p�l���̑傫���͖����ł�����̂Ƃ���B
(1) �[�qD�̓d�ʂ��[���Ƃ���B��Ԃ̒��S��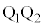 �Ԃ��ړ�����Ԃ̒[�qA�CB�̓d�ʂ����ꂼ�ꋁ�߁A
�Ԃ��ړ�����Ԃ̒[�qA�CB�̓d�ʂ����ꂼ�ꋁ�߁A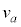 �CL�Cd�CB�Cm�̂����K�v�Ȃ��̂�p���ĕ\���B
�CL�Cd�CB�Cm�̂����K�v�Ȃ��̂�p���ĕ\���B
(2) ��R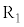 ��
��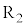 �̒�R�l
�̒�R�l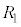 �C
�C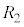 ��
��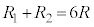 �����Ȃ���
�����Ȃ���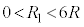 �͈̔͂Œl�߂��邱�Ƃ��ł���B���
�͈̔͂Œl�߂��邱�Ƃ��ł���B���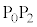 ��ʂ�߂�����̑�Ԃ̑����̕ω�
��ʂ�߂�����̑�Ԃ̑����̕ω�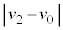 ��
��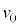 �CL�Cd�CB�Cm�C
�CL�Cd�CB�Cm�C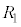 �C
�C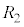 �̂����K�v�Ȃ��̂�p���ĕ\���B�܂��A
�̂����K�v�Ȃ��̂�p���ĕ\���B�܂��A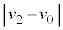 ���ŏ��ƂȂ�悤��
���ŏ��ƂȂ�悤��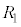 �����߁AR��p���ĕ\���B
�����߁AR��p���ĕ\���B
[��]
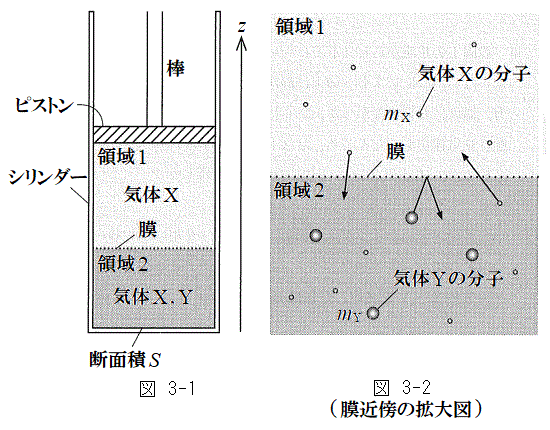 [3]�@�}3-1�̂悤�Ƀs�X�g���̂����f�ʐψ��̃V�����_�[������B�s�X�g���ɂ͖_�����Ă���A�C����ۂ��Ȃ��牔�������Ɋ��炩�ɓ��������Ƃ��ł���B�V�����_�[�ƃs�X�g���ň͂܂ꂽ��Ԃ́A�V�����_�[���̂���ʒu�ɐ����ɌŒ肳�ꂽ����Ȗ��ɂ���ė̈�1�Ɨ̈�2�Ɏd���Ă���B�̈�1�Ɨ̈�2�ɂ͍��v1�����̒P���q���q���z�C��X���A�̈�2�ɂ͋C��X�̂ق���1�����̒P���q���q���z�C��Y�������Ă���B�}3-2�̂悤�ɋC��X�̕��q�͖����Փ˂����ʉ߂ł���̂ɑ��A�C��Y�̕��q�͖���ʉ߂ł��Ȃ��B�V�����_�[�ƃs�X�g���ň͂܂ꂽ��Ԃ̊O�͐^��ł���A���̌�����A���A�V�����_�[�A�s�X�g���̔M�e�ʁA�C�̕��q�ɑ���d�͂̉e���͖����ł���B�s�X�g���͒f�M�ނłł��Ă���B�C��X�̕��q1�̎��ʂ�
[3]�@�}3-1�̂悤�Ƀs�X�g���̂����f�ʐψ��̃V�����_�[������B�s�X�g���ɂ͖_�����Ă���A�C����ۂ��Ȃ��牔�������Ɋ��炩�ɓ��������Ƃ��ł���B�V�����_�[�ƃs�X�g���ň͂܂ꂽ��Ԃ́A�V�����_�[���̂���ʒu�ɐ����ɌŒ肳�ꂽ����Ȗ��ɂ���ė̈�1�Ɨ̈�2�Ɏd���Ă���B�̈�1�Ɨ̈�2�ɂ͍��v1�����̒P���q���q���z�C��X���A�̈�2�ɂ͋C��X�̂ق���1�����̒P���q���q���z�C��Y�������Ă���B�}3-2�̂悤�ɋC��X�̕��q�͖����Փ˂����ʉ߂ł���̂ɑ��A�C��Y�̕��q�͖���ʉ߂ł��Ȃ��B�V�����_�[�ƃs�X�g���ň͂܂ꂽ��Ԃ̊O�͐^��ł���A���̌�����A���A�V�����_�[�A�s�X�g���̔M�e�ʁA�C�̕��q�ɑ���d�͂̉e���͖����ł���B�s�X�g���͒f�M�ނłł��Ă���B�C��X�̕��q1�̎��ʂ�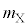 �C�C��Y�̕��q1�̎��ʂ�
�C�C��Y�̕��q1�̎��ʂ�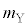 �C�V�����_�[�̓����̒f�ʐς�S�C�A�{�K�h���萔��
�C�V�����_�[�̓����̒f�ʐς�S�C�A�{�K�h���萔��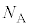 �C�C�̒萔��R�Ƃ���B�����������z�����Ƃ�B�ȉ��̊e�ߒ��ł͋C�̂̏�Ԃ͏\���������ω����邽�߁A�̈�1�̈��͂Ɨ̈�2�̈��͂͂��ꂼ���ɋψ�ł���A�C��X��Y���M�̂��Ƃ�����邱�ƂŃV�����_�[���̉��x�͏�ɋψ�ł���Ƃ݂Ȃ���B
�C�C�̒萔��R�Ƃ���B�����������z�����Ƃ�B�ȉ��̊e�ߒ��ł͋C�̂̏�Ԃ͏\���������ω����邽�߁A�̈�1�̈��͂Ɨ̈�2�̈��͂͂��ꂼ���ɋψ�ł���A�C��X��Y���M�̂��Ƃ�����邱�ƂŃV�����_�[���̉��x�͏�ɋψ�ł���Ƃ݂Ȃ���B
�ȉ��̐ݖ�ɓ�����B
�T�@�͂��߂Ƀs�X�g���͌Œ肳��Ă���A�̈�1�̑̐ς�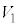 �C���͂�
�C���͂�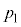 �C�̈�2�̑̐ς�
�C�̈�2�̑̐ς�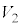 �C���͂�
�C���͂�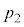 �C�V�����_�[���̉��x��T�ł������B�C�̕��q��z�����̉^���ɒ��ڂ��A�C��X��Y�̕��q�̑��x��z������2��̕��ς����ꂼ��
�C�V�����_�[���̉��x��T�ł������B�C�̕��q��z�����̉^���ɒ��ڂ��A�C��X��Y�̕��q�̑��x��z������2��̕��ς����ꂼ��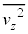 �C
�C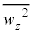 �Ƃ���B�C��Y�̕��q�́A���ɓ�����Ɩ��ɕ��s�ȑ��x�����͈��̂܂ܒe���Փ˂��Ă͂˕Ԃ����Ƃ���B���l�ɁA�C��X��Y�̕��q�̓s�X�g������уV�����_�[�̖ʂɓ�����Ɩʂɕ��s�ȑ��x�����͈��̂܂ܒe���Փ˂��Ă͂˕Ԃ����Ƃ���B���q�Ԃ̏Փ˂͍l�����Ȃ��Ă悢�قNjC�̂͊ł���B
�Ƃ���B�C��Y�̕��q�́A���ɓ�����Ɩ��ɕ��s�ȑ��x�����͈��̂܂ܒe���Փ˂��Ă͂˕Ԃ����Ƃ���B���l�ɁA�C��X��Y�̕��q�̓s�X�g������уV�����_�[�̖ʂɓ�����Ɩʂɕ��s�ȑ��x�����͈��̂܂ܒe���Փ˂��Ă͂˕Ԃ����Ƃ���B���q�Ԃ̏Փ˂͍l�����Ȃ��Ă悢�قNjC�̂͊ł���B
(1) �s�X�g�����C��X�����͂̑傫���̕��ς�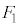 �Ƃ���B
�Ƃ���B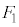 ���A
���A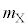 �C
�C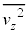 �C
�C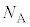 �CS�C
�CS�C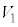 �C
�C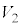 �̂����K�v�Ȃ��̂�p���ĕ\���B
�̂����K�v�Ȃ��̂�p���ĕ\���B
(2) �V�����_�[�̒�ʂ��C��X��Y����鍇�v�̗͂̑傫���̕��ς�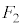 �Ƃ���B
�Ƃ���B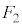 ���A
���A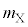 �C
�C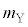 �C
�C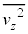 �C
�C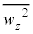 �C
�C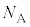 �CS�C
�CS�C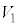 �C
�C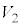 �̂����K�v�Ȃ��̂�p���ĕ\���B
�̂����K�v�Ȃ��̂�p���ĕ\���B
(3) �{���c�}���萔��k�Ƃ��āA�e���q�͈���������蕽�ς���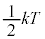 �̉^���G�l���M�[�����B
�̉^���G�l���M�[�����B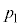 ��
��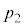 ���AR�CT�C
���AR�CT�C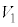 �C
�C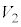 �̂����K�v�Ȃ��̂�p���ĕ\���B
�̂����K�v�Ȃ��̂�p���ĕ\���B
(4) �C��X��Y�̓����G�l���M�[�̍��v���AR�CT��p���ĕ\���B
�U�@���Ƀs�X�g����ݖ�T�̏�Ԃ���킸���ɉ����������Ƃ���A�̈�1�̑̐ς�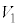 ����
����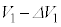 �ɁA�̈�1�̈��͂�
�ɁA�̈�1�̈��͂�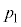 ����
����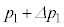 �ɁA�̈�2�̈��͂�
�ɁA�̈�2�̈��͂�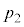 ����
����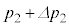 �ɁA�V�����_�[���̉��x��T����
�ɁA�V�����_�[���̉��x��T����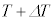 �ɕω������B���̉ߒ��ŋC�̂ƊO���̊ԂŔM�̂��Ƃ�͂Ȃ������B�ȉ��̐ݖ�ł́A
�ɕω������B���̉ߒ��ŋC�̂ƊO���̊ԂŔM�̂��Ƃ�͂Ȃ������B�ȉ��̐ݖ�ł́A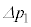 �C
�C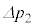 �C
�C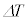 �C
�C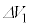 �͂��ꂼ��
�͂��ꂼ��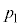 �C
�C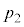 �CT�C
�CT�C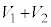 ���\�������Ȑ��̔����ʂƂ��A�����ʂǂ����̐ς͖����ł���Ƃ���B
���\�������Ȑ��̔����ʂƂ��A�����ʂǂ����̐ς͖����ł���Ƃ���B
(1) ���x�ω�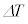 ���A
���A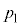 �CR�C
�CR�C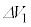 ��p���ĕ\���B
��p���ĕ\���B
(2)  �����藧�B
�����藧�B �ɓ��鐔�����߂�B
�ɓ��鐔�����߂�B
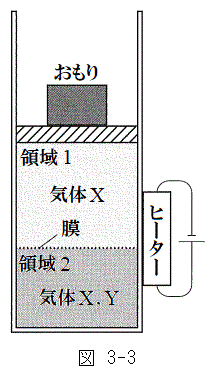 �V�@�ݖ�T�̏�Ԃ���s�X�g���ɂ��Ă���_�����O���A��������V�����_�[�ɐڂ��Ȃ��悤�Ƀs�X�g���̏�ɐÂ��ɏ悹���Ƃ���A�̈�1�Ɨ̈�2�̑̐ρA���́A���x�ɕω��͂Ȃ������B����ɐ}3-3�̂悤�Ƀq�[�^�[���V�����_�[�ɐڐG�����C�̂����߂��Ƃ���A�s�X�g����������艟���オ�����B�̈�1�̑̐ς�
�V�@�ݖ�T�̏�Ԃ���s�X�g���ɂ��Ă���_�����O���A��������V�����_�[�ɐڂ��Ȃ��悤�Ƀs�X�g���̏�ɐÂ��ɏ悹���Ƃ���A�̈�1�Ɨ̈�2�̑̐ρA���́A���x�ɕω��͂Ȃ������B����ɐ}3-3�̂悤�Ƀq�[�^�[���V�����_�[�ɐڐG�����C�̂����߂��Ƃ���A�s�X�g����������艟���オ�����B�̈�1�̑̐ς�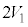 �ɂȂ����Ƃ���Ńq�[�^�[���V�����_�[���痣�����B
�ɂȂ����Ƃ���Ńq�[�^�[���V�����_�[���痣�����B
(1) ���̂Ƃ��̃V�����_�[���̉��x���AT�C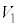 �C
�C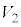 ��p���ĕ\���B
��p���ĕ\���B
(2) �C��X��Y���z�������M�ʂ̍��v���AR�CT�C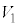 �C
�C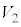 ��p���ĕ\���B
��p���ĕ\���B [��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B