���啨��'22�N�O��[3]
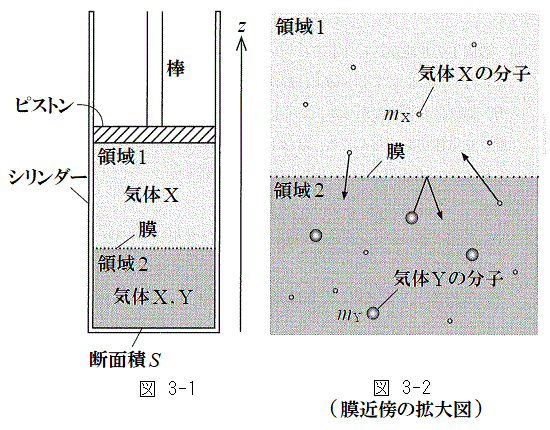 �}3-1�̂悤�Ƀs�X�g���̂����f�ʐψ��̃V�����_�[������B�s�X�g���ɂ͖_�����Ă���A�C����ۂ��Ȃ��牔�������Ɋ��炩�ɓ��������Ƃ��ł���B�V�����_�[�ƃs�X�g���ň͂܂ꂽ��Ԃ́A�V�����_�[���̂���ʒu�ɐ����ɌŒ肳�ꂽ����Ȗ��ɂ���ė̈�1�Ɨ̈�2�Ɏd���Ă���B�̈�1�Ɨ̈�2�ɂ͍��v1�����̒P���q���q���z�C��X���A�̈�2�ɂ͋C��X�̂ق���1�����̒P���q���q���z�C��Y�������Ă���B�}3-2�̂悤�ɋC��X�̕��q�͖����Փ˂����ʉ߂ł���̂ɑ��A�C��Y�̕��q�͖���ʉ߂ł��Ȃ��B�V�����_�[�ƃs�X�g���ň͂܂ꂽ��Ԃ̊O�͐^��ł���A���̌�����A���A�V�����_�[�A�s�X�g���̔M�e�ʁA�C�̕��q�ɑ���d�͂̉e���͖����ł���B�s�X�g���͒f�M�ނłł��Ă���B�C��X�̕��q1�̎��ʂ�
�}3-1�̂悤�Ƀs�X�g���̂����f�ʐψ��̃V�����_�[������B�s�X�g���ɂ͖_�����Ă���A�C����ۂ��Ȃ��牔�������Ɋ��炩�ɓ��������Ƃ��ł���B�V�����_�[�ƃs�X�g���ň͂܂ꂽ��Ԃ́A�V�����_�[���̂���ʒu�ɐ����ɌŒ肳�ꂽ����Ȗ��ɂ���ė̈�1�Ɨ̈�2�Ɏd���Ă���B�̈�1�Ɨ̈�2�ɂ͍��v1�����̒P���q���q���z�C��X���A�̈�2�ɂ͋C��X�̂ق���1�����̒P���q���q���z�C��Y�������Ă���B�}3-2�̂悤�ɋC��X�̕��q�͖����Փ˂����ʉ߂ł���̂ɑ��A�C��Y�̕��q�͖���ʉ߂ł��Ȃ��B�V�����_�[�ƃs�X�g���ň͂܂ꂽ��Ԃ̊O�͐^��ł���A���̌�����A���A�V�����_�[�A�s�X�g���̔M�e�ʁA�C�̕��q�ɑ���d�͂̉e���͖����ł���B�s�X�g���͒f�M�ނłł��Ă���B�C��X�̕��q1�̎��ʂ�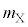 �C�C��Y�̕��q1�̎��ʂ�
�C�C��Y�̕��q1�̎��ʂ�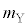 �C�V�����_�[�̓����̒f�ʐς�S�C�A�{�K�h���萔��
�C�V�����_�[�̓����̒f�ʐς�S�C�A�{�K�h���萔��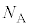 �C�C�̒萔��R�Ƃ���B�����������z�����Ƃ�B�ȉ��̊e�ߒ��ł͋C�̂̏�Ԃ͏\���������ω����邽�߁A�̈�1�̈��͂Ɨ̈�2�̈��͂͂��ꂼ���ɋψ�ł���A�C��X��Y���M�̂��Ƃ�����邱�ƂŃV�����_�[���̉��x�͏�ɋψ�ł���Ƃ݂Ȃ���B
�C�C�̒萔��R�Ƃ���B�����������z�����Ƃ�B�ȉ��̊e�ߒ��ł͋C�̂̏�Ԃ͏\���������ω����邽�߁A�̈�1�̈��͂Ɨ̈�2�̈��͂͂��ꂼ���ɋψ�ł���A�C��X��Y���M�̂��Ƃ�����邱�ƂŃV�����_�[���̉��x�͏�ɋψ�ł���Ƃ݂Ȃ���B
�ȉ��̐ݖ�ɓ�����B
�T�@�͂��߂Ƀs�X�g���͌Œ肳��Ă���A�̈�1�̑̐ς�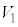 �C���͂�
�C���͂�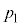 �C�̈�2�̑̐ς�
�C�̈�2�̑̐ς�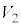 �C���͂�
�C���͂�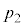 �C�V�����_�[���̉��x��T�ł������B�C�̕��q��z�����̉^���ɒ��ڂ��A�C��X��Y�̕��q�̑��x��z������2��̕��ς����ꂼ��
�C�V�����_�[���̉��x��T�ł������B�C�̕��q��z�����̉^���ɒ��ڂ��A�C��X��Y�̕��q�̑��x��z������2��̕��ς����ꂼ��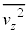 �C
�C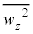 �Ƃ���B�C��Y�̕��q�́A���ɓ�����Ɩ��ɕ��s�ȑ��x�����͈��̂܂ܒe���Փ˂��Ă͂˕Ԃ����Ƃ���B���l�ɁA�C��X��Y�̕��q�̓s�X�g������уV�����_�[�̖ʂɓ�����Ɩʂɕ��s�ȑ��x�����͈��̂܂ܒe���Փ˂��Ă͂˕Ԃ����Ƃ���B���q�Ԃ̏Փ˂͍l�����Ȃ��Ă悢�قNjC�̂͊ł���B
�Ƃ���B�C��Y�̕��q�́A���ɓ�����Ɩ��ɕ��s�ȑ��x�����͈��̂܂ܒe���Փ˂��Ă͂˕Ԃ����Ƃ���B���l�ɁA�C��X��Y�̕��q�̓s�X�g������уV�����_�[�̖ʂɓ�����Ɩʂɕ��s�ȑ��x�����͈��̂܂ܒe���Փ˂��Ă͂˕Ԃ����Ƃ���B���q�Ԃ̏Փ˂͍l�����Ȃ��Ă悢�قNjC�̂͊ł���B
(1) �s�X�g�����C��X�����͂̑傫���̕��ς�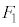 �Ƃ���B
�Ƃ���B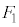 ���A
���A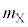 �C
�C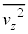 �C
�C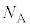 �CS�C
�CS�C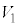 �C
�C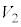 �̂����K�v�Ȃ��̂�p���ĕ\���B
�̂����K�v�Ȃ��̂�p���ĕ\���B
(2) �V�����_�[�̒�ʂ��C��X��Y����鍇�v�̗͂̑傫���̕��ς�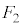 �Ƃ���B
�Ƃ���B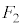 ���A
���A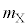 �C
�C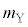 �C
�C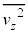 �C
�C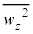 �C
�C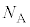 �CS�C
�CS�C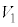 �C
�C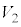 �̂����K�v�Ȃ��̂�p���ĕ\���B
�̂����K�v�Ȃ��̂�p���ĕ\���B
(3) �{���c�}���萔��k�Ƃ��āA�e���q�͈���������蕽�ς���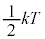 �̉^���G�l���M�[�����B
�̉^���G�l���M�[�����B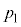 ��
��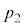 ���AR�CT�C
���AR�CT�C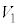 �C
�C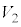 �̂����K�v�Ȃ��̂�p���ĕ\���B
�̂����K�v�Ȃ��̂�p���ĕ\���B
(4) �C��X��Y�̓����G�l���M�[�̍��v���AR�CT��p���ĕ\���B
�U�@���Ƀs�X�g����ݖ�T�̏�Ԃ���킸���ɉ����������Ƃ���A�̈�1�̑̐ς�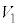 ����
����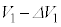 �ɁA�̈�1�̈��͂�
�ɁA�̈�1�̈��͂�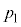 ����
����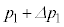 �ɁA�̈�2�̈��͂�
�ɁA�̈�2�̈��͂�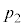 ����
����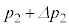 �ɁA�V�����_�[���̉��x��T����
�ɁA�V�����_�[���̉��x��T����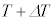 �ɕω������B���̉ߒ��ŋC�̂ƊO���̊ԂŔM�̂��Ƃ�͂Ȃ������B�ȉ��̐ݖ�ł́A
�ɕω������B���̉ߒ��ŋC�̂ƊO���̊ԂŔM�̂��Ƃ�͂Ȃ������B�ȉ��̐ݖ�ł́A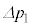 �C
�C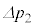 �C
�C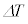 �C
�C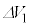 �͂��ꂼ��
�͂��ꂼ��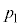 �C
�C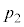 �CT�C
�CT�C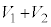 ���\�������Ȑ��̔����ʂƂ��A�����ʂǂ����̐ς͖����ł���Ƃ���B
���\�������Ȑ��̔����ʂƂ��A�����ʂǂ����̐ς͖����ł���Ƃ���B
(1) ���x�ω�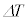 ���A
���A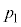 �CR�C
�CR�C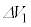 ��p���ĕ\���B
��p���ĕ\���B
(2)  �����藧�B
�����藧�B �ɓ��鐔�����߂�B
�ɓ��鐔�����߂�B
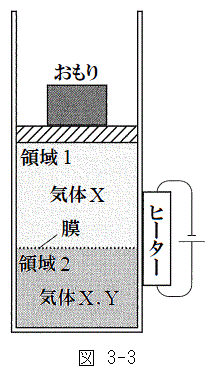 �V�@�ݖ�T�̏�Ԃ���s�X�g���ɂ��Ă���_�����O���A��������V�����_�[�ɐڂ��Ȃ��悤�Ƀs�X�g���̏�ɐÂ��ɏ悹���Ƃ���A�̈�1�Ɨ̈�2�̑̐ρA���́A���x�ɕω��͂Ȃ������B����ɐ}3-3�̂悤�Ƀq�[�^�[���V�����_�[�ɐڐG�����C�̂����߂��Ƃ���A�s�X�g����������艟���オ�����B�̈�1�̑̐ς�
�V�@�ݖ�T�̏�Ԃ���s�X�g���ɂ��Ă���_�����O���A��������V�����_�[�ɐڂ��Ȃ��悤�Ƀs�X�g���̏�ɐÂ��ɏ悹���Ƃ���A�̈�1�Ɨ̈�2�̑̐ρA���́A���x�ɕω��͂Ȃ������B����ɐ}3-3�̂悤�Ƀq�[�^�[���V�����_�[�ɐڐG�����C�̂����߂��Ƃ���A�s�X�g����������艟���オ�����B�̈�1�̑̐ς�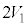 �ɂȂ����Ƃ���Ńq�[�^�[���V�����_�[���痣�����B
�ɂȂ����Ƃ���Ńq�[�^�[���V�����_�[���痣�����B
(1) ���̂Ƃ��̃V�����_�[���̉��x���AT�C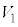 �C
�C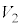 ��p���ĕ\���B
��p���ĕ\���B
(2) �C��X��Y���z�������M�ʂ̍��v���AR�CT�C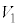 �C
�C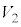 ��p���ĕ\���B
��p���ĕ\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�{��́A[1]�C[2]�Ƃ͈���āA�C��X�͒ʂ����C��Y�͒ʂ��Ȃ����A�Ƃ���������Ȃ��ݒ�ŁA���X�l�����݂܂��B�C��X�͗̈�1�C�̈�2���킹���̐�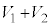 �̗̈�ɑ��݂��A�C��Y�͗̈�2�݂̂ɑ��݂���A�ƍl���܂��B�U�́A�|�A�b�\���̊W�����g���Ȃ��ݒ�ł����A�|�A�b�\���̊W�����o�̍ۂɂǂ��l�������A�Ƃ������Ƃ��v���o���悤�ɂ��܂��B
�̗̈�ɑ��݂��A�C��Y�͗̈�2�݂̂ɑ��݂���A�ƍl���܂��B�U�́A�|�A�b�\���̊W�����g���Ȃ��ݒ�ł����A�|�A�b�\���̊W�����o�̍ۂɂǂ��l�������A�Ƃ������Ƃ��v���o���悤�ɂ��܂��B
���ꂪ�A�C�̕��q�̎�͐ςł����A��p����p�̖@�����A����t�����̗͐�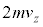 ���s�X�g���ɗ^���܂��B�C�̕��q��z�����ɓ����͈͂̋�����l�Ƃ��āA�s�X�g���Ƃ͋t���̕ǂŒ��˕Ԃ��ĉ���
���s�X�g���ɗ^���܂��B�C�̕��q��z�����ɓ����͈͂̋�����l�Ƃ��āA�s�X�g���Ƃ͋t���̕ǂŒ��˕Ԃ��ĉ���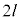 �i��Ŗ߂��Ă��鎞�Ԃ�
�i��Ŗ߂��Ă��鎞�Ԃ�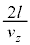 �C1�b�ԂɃs�X�g����
�C1�b�ԂɃs�X�g����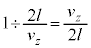 ��Փ˂���̂ŁA�s�X�g����1�b�Ԃɂ��̋C�̕��q�����͐ς�
��Փ˂���̂ŁA�s�X�g����1�b�Ԃɂ��̋C�̕��q�����͐ς�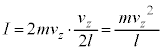 �ł��B
�ł��B
�C��1������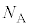 �̋C�̕��q������̂ŁA1�����̋C�̂���s�X�g�������F�C�����A1�b�ԂɎ�͐ς́AI��
�̋C�̕��q������̂ŁA1�����̋C�̂���s�X�g�������F�C�����A1�b�ԂɎ�͐ς́AI��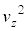 �ϒl
�ϒl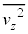 �Œu��������
�Œu��������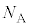 �{���邱�Ƃɂ��A
�{���邱�Ƃɂ��A 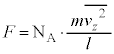 �@����@
�@����@�C�̂���L����̐ς�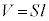 �ł��B�s�X�g����1�����̋C�̂���鈳��P��(���z�C�����Q��)�A��F��ʐ�S�Ŋ����āA
�ł��B�s�X�g����1�����̋C�̂���鈳��P��(���z�C�����Q��)�A��F��ʐ�S�Ŋ����āA 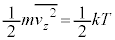 �@����A
�@����A�����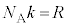 ���A1�����̋C�̂̈���P�́A
���A1�����̋C�̂̈���P�́A 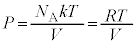 �@����B�@(����́A1�����̗��z�C�̂���ԕ������ł�)
�@����B�@(����́A1�����̗��z�C�̂���ԕ������ł�)�����G�l���M�[�́A�C�̕��q1�ł͇A��3�����Ƃ���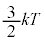 �C1�����̋C�̂ł͋C�̕��q
�C1�����̋C�̂ł͋C�̕��q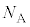 �ŁA
�ŁA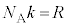 ���A
���A 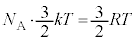 �@����C
�@����C
(1) �s�X�g�����C��X�����͂̑傫���̕���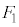 �́A�@��
�́A�@��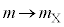 �C
�C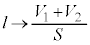 �Ƃ��āA
�Ƃ��āA 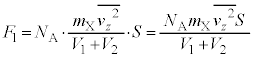 ......[��]
......[��]
(2) �V�����_�[�̒�ʂ��C��X�����͂�(1)��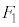 �ł��B�C��Y�����͂̑傫���̕���
�ł��B�C��Y�����͂̑傫���̕���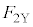 �́A�@��
�́A�@��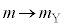 �C
�C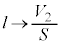 �C
�C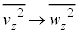 �Ƃ��āA
�Ƃ��āA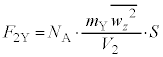 �CX��Y�����킹���
�CX��Y�����킹���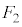 �́A
�́A 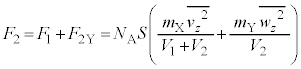 �@......[��]
�@......[��]
(3) �O�q�̂悤�ɁA�̈�1�ɂ͋C��X�̂ݑ��݂���̂ł����A�C��X�͗̈�1�ɂ��̈�2�ɂ����݂���̂ŁA�C��X����L����̐ς�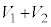 �ł��B
�ł��B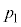 �́A�B��
�́A�B��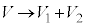 �C
�C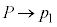 �Ƃ��邱�Ƃɂ��A
�Ƃ��邱�Ƃɂ��A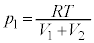 ......[��]
......[��] �̈�2�ŋC��Y�ɂ�镪��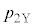 �́A�B��
�́A�B��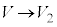 �C
�C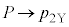 �Ƃ��邱�Ƃɂ��A
�Ƃ��邱�Ƃɂ��A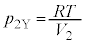 �C�C��X�ɂ�镪����
�C�C��X�ɂ�镪����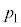 �ŁA
�ŁA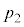 �́A
�́A 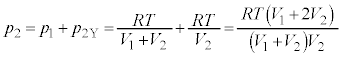 ......[��]
......[��]
(4) �C��X�C�C��Y�Ƃ���1�����ʼn��x��T�Ȃ̂ŁA�C���A�C��X�ƋC��Y�������G�l���M�[�̍��v�́A 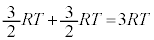 ......[��]
......[��]
�U(1) 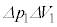 ������̂ŁA���̊Ԃ��C�̂������d����
������̂ŁA���̊Ԃ��C�̂������d����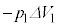 �ł��B�T(4)�������G�l���M�|�̑����͋C��X�ƋC��Y���킹��
�ł��B�T(4)�������G�l���M�|�̑����͋C��X�ƋC��Y���킹��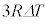 �C�M�͊w���@�����A�C�͔̂M�����Ƃ肵�Ă��Ȃ��̂ŁA
�C�M�͊w���@�����A�C�͔̂M�����Ƃ肵�Ă��Ȃ��̂ŁA 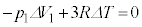 �@��
�@�� 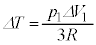 ......[��]
......[��]
������������̏�ԂŋC��X����ԕ������F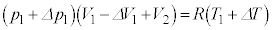 �@����E
�@����E
�E�|�D�Ƃ���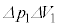 ������ƁA
������ƁA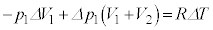 �@����F(1)�̌��ʂ��A
�@����F(1)�̌��ʂ��A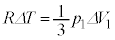 �C������F�ɑ�����A
�C������F�ɑ�����A  �ɓ���̂́A
�ɓ���̂́A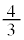 ......[��]
......[��]
�V(1) �C��X���s�X�g���������͕͂ω����Ȃ��̂ŁA�C��X�̕ω����舳�ω��ł��B�C��X�̈��͂�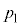 �̂܂ܕω����܂���B�q�[�^�[�𗣂����Ƃ��A�C��X����߂�̐ς�
�̂܂ܕω����܂���B�q�[�^�[�𗣂����Ƃ��A�C��X����߂�̐ς�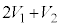 �Ȃ̂ŁA���̏�Ԃł̉��x��
�Ȃ̂ŁA���̏�Ԃł̉��x��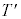 �Ƃ��āA�C��X�̏�ԕ������F
�Ƃ��āA�C��X�̏�ԕ������F 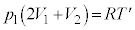 �@����G
�@����G�G���D���A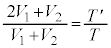 �@��
�@�� 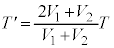 ......[��]
......[��]
�����Œ肳��Ă��ē������C��Y����ϕω�����̂ŁA�C��Y���z�������M����σ�����M�̎����A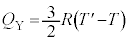
�C��X�ƋC��Y���z�������M�ʂ̍��v�́A(1)�̌��ʂ�p���āA 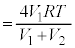 ......[��]
......[��]�ʉ��D�C��X�CY�͂Ƃ���1���������݂���̂ŁA�����G�l���M�[�͇C�ŗ^�����A�����G�l���M�[�̕ω��́A
�C�̂̂����d���́A���̈���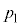 �̂��Ƃő̐ς�
�̂��Ƃő̐ς�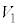 ��������̂ŁA(3)�̌��ʂ�p���āA
��������̂ŁA(3)�̌��ʂ�p���āA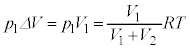 �M�͊w���@�����A�C�̂��z�������M�ʂ̍��vQ�́A
�M�͊w���@�����A�C�̂��z�������M�ʂ̍��vQ�́A
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 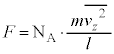 �@����@
�@����@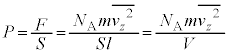
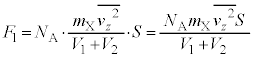 ......[��]
......[��]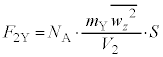 �CX��Y�����킹���
�CX��Y�����킹���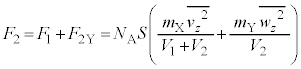 �@......[��]
�@......[��]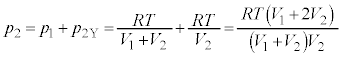 ......[��]
......[��]