������w2025�N�O�������������
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
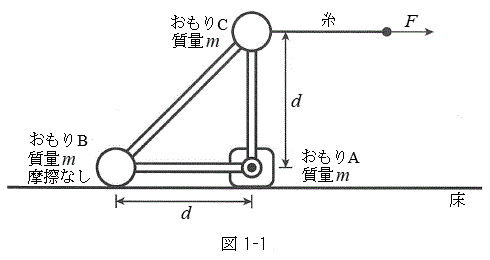 [1]�@�}1-1�̂悤�ɁA3�̂������3�{�̖_���݂��ɌŒ肵�����̂̉^�����l����B�������A�}1-2�̂悤�ɁA������A�ɑ���2�{�̖_�͂Ȃ߂炩�ɉ�]�ł���B�͂��ߕ��̂́A�}1-1�̂悤�ɁA������A�Ƃ�����B�������ȏ��ɐڂ���悤�ɒu����Ă���A������C�͂�����A�̐^��ɂ���B������C�ɂ͐����ɒ���ꂽ�����Ȃ���Ă���A����}�̉E�����Ɉ����͂̑傫����F�Ƃ���B3�̂�����̎��ʂ͂������m�ł���A�_�Ǝ��̎��ʂ͍l���Ȃ��Ă悢�B������A���炨����B�܂ł̋����A����т�����A���炨����C�܂ł̋����͂������d�ł���A������̑傫���͍l���Ȃ��Ă悢�B�܂��A�d�͉����x�̑傫����
[1]�@�}1-1�̂悤�ɁA3�̂������3�{�̖_���݂��ɌŒ肵�����̂̉^�����l����B�������A�}1-2�̂悤�ɁA������A�ɑ���2�{�̖_�͂Ȃ߂炩�ɉ�]�ł���B�͂��ߕ��̂́A�}1-1�̂悤�ɁA������A�Ƃ�����B�������ȏ��ɐڂ���悤�ɒu����Ă���A������C�͂�����A�̐^��ɂ���B������C�ɂ͐����ɒ���ꂽ�����Ȃ���Ă���A����}�̉E�����Ɉ����͂̑傫����F�Ƃ���B3�̂�����̎��ʂ͂������m�ł���A�_�Ǝ��̎��ʂ͍l���Ȃ��Ă悢�B������A���炨����B�܂ł̋����A����т�����A���炨����C�܂ł̋����͂������d�ł���A������̑傫���͍l���Ȃ��Ă悢�B�܂��A�d�͉����x�̑傫����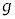 �Ƃ���B
�Ƃ���B
�T�@�܂��A������A�����ɌŒ肳��Ă���ꍇ���l����B
(1) �}1-1�̏�Ԃɂ����āAF�����X�ɑ傫�����Ă������Ƃ���AF������傫���ɒB�����Ƃ��ɂ�����B���������痣�ꂽ�B���̂Ƃ���F�����߂�B
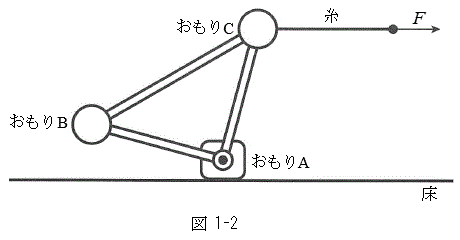 (2) �������������āA�}1-2�̂悤�ɕ��̂��X���Ă������Ƃ��l����B������B�������痣��Ă��玅�������͂������d���̑傫����W�Ƃ���BW������傫��
(2) �������������āA�}1-2�̂悤�ɕ��̂��X���Ă������Ƃ��l����B������B�������痣��Ă��玅�������͂������d���̑傫����W�Ƃ���BW������傫��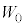 ����ƁA���͓̂|��āA������C�͏��ɏՓ˂���B
����ƁA���͓̂|��āA������C�͏��ɏՓ˂���B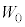 �����߂�B
�����߂�B
�U�@���ɁA������A�����ɌŒ肳��Ă��Ȃ��ꍇ���l����B�}1-1�̂悤�ɂ�����A�Ƃ�����B�͏��ɐڂ��Ă���B������A�Ə��Ƃ̊Ԃ̐Î~���C�W����μ (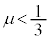 )�ł���A������B�Ə��Ƃ̊Ԃɂ͖��C�͂Ȃ��B
)�ł���A������B�Ə��Ƃ̊Ԃɂ͖��C�͂Ȃ��B
(1) F���������A���̂��Î~���Ă���Ƃ��A������B��������鐂���R�͂̑傫�����AF���܂ގ��ŕ\���B
(2) �O��U(1)�̂Ƃ��A������A��������鐂���R�͂̑傫�����AF���܂ގ��ŕ\���B
(3) F�����X�ɑ傫�����Ă������Ƃ���AF������傫���ɒB�����Ƃ��ɁA������B�����ɐڂ����܂ܕ��̂��E�ɓ����n�߂��B���̂Ƃ���F�����߂�B
 �V�@�Ō�ɁA������A�Ƃ�����B�����ɐڂ����܂܁A���̂��E�ɓ����Ă���ꍇ���l����B������A�Ə��Ƃ̊Ԃ̓����C�W����
�V�@�Ō�ɁA������A�Ƃ�����B�����ɐڂ����܂܁A���̂��E�ɓ����Ă���ꍇ���l����B������A�Ə��Ƃ̊Ԃ̓����C�W����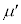 (
(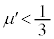 )�ł���A������B�Ə��Ƃ̊Ԃɂ͖��C�͂Ȃ��B
)�ł���A������B�Ə��Ƃ̊Ԃɂ͖��C�͂Ȃ��B
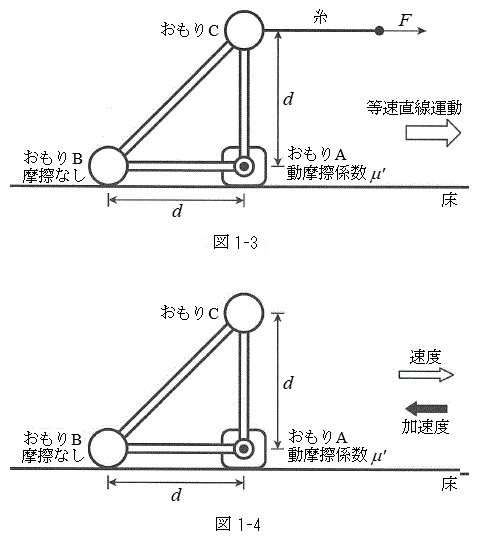
(1) �}1-3�̂悤�ɁA���̂����������^�����Ă���Ƃ���F�����߂�B
(2) ���������̂���߂�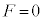 �ɂ���ƁA���͓̂������x�Ō�������B���̂Ƃ��A�}1-4�Ɏ����悤�ɁA�����x�͑��x�Ƌt�����ł���A���̑傫����a (
�ɂ���ƁA���͓̂������x�Ō�������B���̂Ƃ��A�}1-4�Ɏ����悤�ɁA�����x�͑��x�Ƌt�����ł���A���̑傫����a (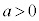 )�Ƃ���B������B��������鐂���R�͂̑傫�����Aa���܂ގ��ŕ\���B
)�Ƃ���B������B��������鐂���R�͂̑傫�����Aa���܂ގ��ŕ\���B
(3) �O��V(2)��a�����߂�B
[��]
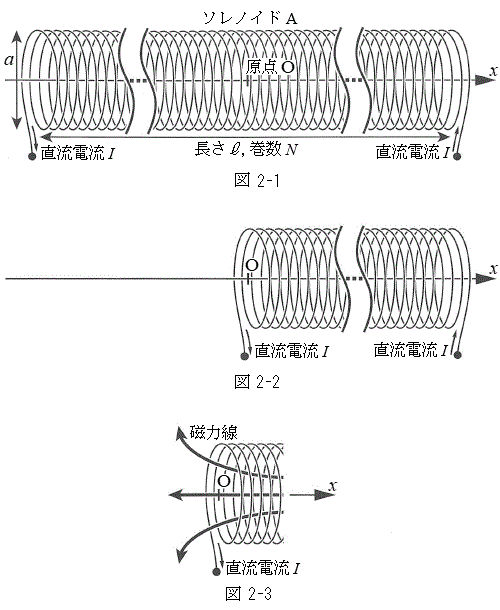 [2]�@�T�@�}2-1�̂悤�ɁA�^�ɒ��aa�C����
[2]�@�T�@�}2-1�̂悤�ɁA�^�ɒ��aa�C����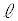 �C����N�̃\���m�C�hA������B���̒��S����x���ɂƂ�A���_O���\���m�C�hA�̒��S�ƂȂ�悤�ɂƂ����Bx���͉E�����𐳂Ƃ���B
�C����N�̃\���m�C�hA������B���̒��S����x���ɂƂ�A���_O���\���m�C�hA�̒��S�ƂȂ�悤�ɂƂ����Bx���͉E�����𐳂Ƃ���B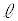 ��a���\���ɑ傫���B�\���m�C�hA�ɉE���獶�Ɍ����Ĉ��̑傫��I�̒����d���𗬂��B�^��̓�����(���C�萔)��
��a���\���ɑ傫���B�\���m�C�hA�ɉE���獶�Ɍ����Ĉ��̑傫��I�̒����d���𗬂��B�^��̓�����(���C�萔)��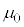 �Ƃ��Ĉȉ��̐ݖ�ɓ�����B
�Ƃ��Ĉȉ��̐ݖ�ɓ�����B
(1) ���_O�̎������x�̑傫��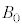 �����߂�B
�����߂�B
(2) �\���m�C�hA�𒆉��œ����č�����(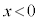 )����菜���A�}2-2�̂悤�ɁA�E���獶�Ɍ����Ĉ��̑傫��I�̒����d���𗬂����B���̂Ƃ��A���_O�t�߂̎��͐��͐}2-3�̂悤�ɕ\�����B���_O�ɂ����鎥�����x�̑傫��
)����菜���A�}2-2�̂悤�ɁA�E���獶�Ɍ����Ĉ��̑傫��I�̒����d���𗬂����B���̂Ƃ��A���_O�t�߂̎��͐��͐}2-3�̂悤�ɕ\�����B���_O�ɂ����鎥�����x�̑傫��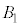 ���A
���A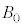 ��p���ĕ\���B
��p���ĕ\���B
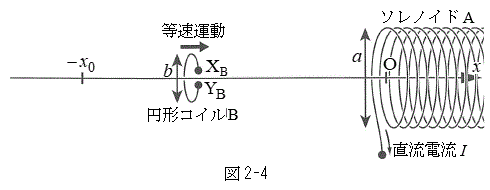 �U�@�}2-4�̂悤�ɁA�ݖ�T(1)�ł̒���
�U�@�}2-4�̂悤�ɁA�ݖ�T(1)�ł̒���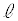 �̃\���m�C�hA���A���S����x���A���[�ʒ��S�����_O�ƂȂ�悤�ɌŒ肵�A�E���獶�Ɍ����Ĉ��̑傫��I�̒����d���𗬂��B����ɁA���ab (
�̃\���m�C�hA���A���S����x���A���[�ʒ��S�����_O�ƂȂ�悤�ɌŒ肵�A�E���獶�Ɍ����Ĉ��̑傫��I�̒����d���𗬂��B����ɁA���ab (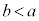 )�C����1�̉~�`�R�C��B���A�ʒu
)�C����1�̉~�`�R�C��B���A�ʒu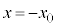 (
(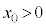 )����\���m�C�hA�����̈ʒu
)����\���m�C�hA�����̈ʒu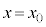 �܂œ����^��������B�~�`�R�C��B�̒��S�͏��x����ɂ���A�R�C���ʂ�x���ɐ����ł���B
�܂œ����^��������B�~�`�R�C��B�̒��S�͏��x����ɂ���A�R�C���ʂ�x���ɐ����ł���B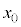 ��
��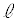 ���\���ɏ������B�܂��A�~�`�R�C��B�ɂ͎��ʂ̎�O���ɒ[�q
���\���ɏ������B�܂��A�~�`�R�C��B�ɂ͎��ʂ̎�O���ɒ[�q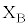 �C
�C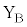 ������B���̒[�q�ԋ����͏\���ɏ������A�~�`�R�C��B�̓d�C��R�Ǝ��ȃC���_�N�^���X�͖����ł���B
������B���̒[�q�ԋ����͏\���ɏ������A�~�`�R�C��B�̓d�C��R�Ǝ��ȃC���_�N�^���X�͖����ł���B
(1) �[�q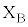 �C
�C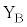 �Ԃɒ�R�lR�̓d�C��R��ڑ����A�~�`�R�C��B���^���������B�~�`�R�C��B���т��������Z������
�Ԃɒ�R�lR�̓d�C��R��ڑ����A�~�`�R�C��B���^���������B�~�`�R�C��B���т��������Z������ �̊Ԃ�
�̊Ԃ�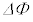 �����ω������Ƃ��A�~�`�R�C��B�ɗ����d���̑傫��
�����ω������Ƃ��A�~�`�R�C��B�ɗ����d���̑傫��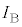 �����߂�B
�����߂�B 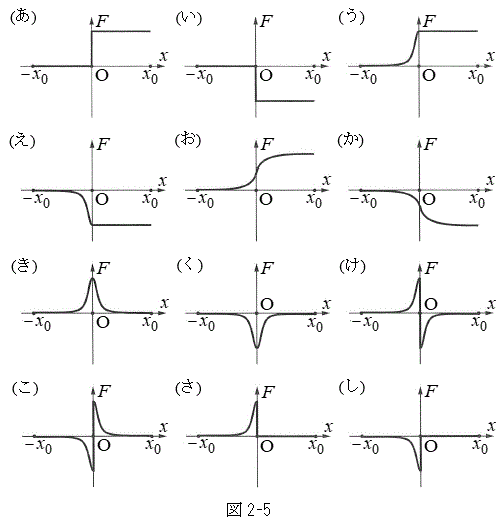 (2) �~�`�R�C��B�S�̂����ꂩ���͂�F�Ƃ���BF�͉E�����𐳂Ƃ���B�O��U(1)�Ɠ��l�ɒ[�q
(2) �~�`�R�C��B�S�̂����ꂩ���͂�F�Ƃ���BF�͉E�����𐳂Ƃ���B�O��U(1)�Ɠ��l�ɒ[�q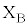 �C
�C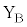 �Ԃɒ�R�lR�̓d�C��R��ڑ����A�~�`�R�C��B���ʒu
�Ԃɒ�R�lR�̓d�C��R��ڑ����A�~�`�R�C��B���ʒu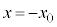 ����
����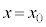 �܂ő���
�܂ő���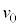 �œ����^���������Ƃ��Ax��F�̊W��\���O���t�̊T�`�Ƃ��čł��K�Ȃ��̂�}2-5��(��)�`(��)�����I��œ�����B
�œ����^���������Ƃ��Ax��F�̊W��\���O���t�̊T�`�Ƃ��čł��K�Ȃ��̂�}2-5��(��)�`(��)�����I��œ�����B
(3) �O��U(2)�ɂ����āA�d�C��R�̒�R�l��R����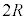 �ɂ���ƁAF�̑傫���̍ő�l�͉��{�ɂȂ邩�A���R�ƂƂ��ɓ�����B
�ɂ���ƁAF�̑傫���̍ő�l�͉��{�ɂȂ邩�A���R�ƂƂ��ɓ�����B 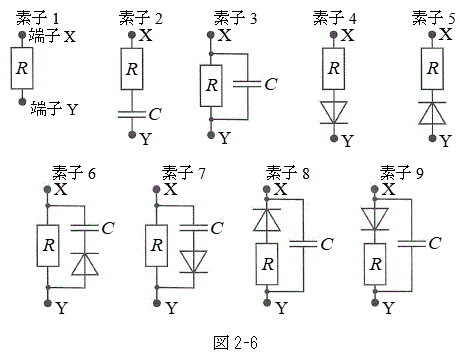 (4) �}2-6�Ɏ����f�q1�`9�́A��R�lR�̓d�C��R�A�d�C�e��C�̃R���f���T�[�A�_�C�I�[�h����Ȃ�B�_�C�I�[�h�ł́A�������ɂ͒�R0�œd��������A�t�����ɂ͗���Ȃ����̂Ƃ���B�Ⴆ�Αf�q4�ɂ����ẮA���ʉ������ɂ͓d��������A������ɂ͗���Ȃ��B
(4) �}2-6�Ɏ����f�q1�`9�́A��R�lR�̓d�C��R�A�d�C�e��C�̃R���f���T�[�A�_�C�I�[�h����Ȃ�B�_�C�I�[�h�ł́A�������ɂ͒�R0�œd��������A�t�����ɂ͗���Ȃ����̂Ƃ���B�Ⴆ�Αf�q4�ɂ����ẮA���ʉ������ɂ͓d��������A������ɂ͗���Ȃ��B
�\���m�C�hA�ɗ��������d���̌������t�ɂ��A������E�Ɍ����Ĉ��̑傫��I�̒����d���𗬂����B�����ŁA�~�`�R�C��B�̒[�q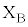 �C
�C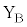 �Ԃɑf�q1�`9�̂������I��Őڑ����A�~�`�R�C��B���ʒu
�Ԃɑf�q1�`9�̂������I��Őڑ����A�~�`�R�C��B���ʒu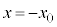 ����
����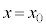 �܂ő���
�܂ő���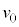 �œ����^��������ꍇ���l����B�������A�~�`�R�C��B�̒[�q
�œ����^��������ꍇ���l����B�������A�~�`�R�C��B�̒[�q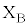 �ɑf�q�̒[�qX���A�[�q
�ɑf�q�̒[�qX���A�[�q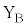 �ɑf�q�̒[�qY��ڑ�������̂Ƃ���B���̂Ƃ��Ax��F�̊W���A�ݖ�U(2)�ƑS�������ɂȂ�f�q��}2-6�̑f�q1�`9���炷�ׂđI�сA�ԍ��œ�����B
�ɑf�q�̒[�qY��ڑ�������̂Ƃ���B���̂Ƃ��Ax��F�̊W���A�ݖ�U(2)�ƑS�������ɂȂ�f�q��}2-6�̑f�q1�`9���炷�ׂđI�сA�ԍ��œ�����B
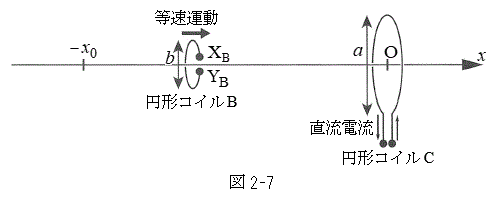 �V�@�}2-7�̂悤�ɁA�}2-4�̏�Ԃ���\���m�C�hA����菜���A����ɒ��aa�C����1�̉~�`�R�C��C���Œ肵���B�~�`�R�C��C�̒��S�͌��_O�Ɉ�v���A�R�C���ʂ�x���ɐ����ł���B�~�`�R�C��C�Ɉ��̑傫���̒����d�����A�����猩�Ĕ����v���ɗ����Ď�������B�~�`�R�C��B�̒[�q
�V�@�}2-7�̂悤�ɁA�}2-4�̏�Ԃ���\���m�C�hA����菜���A����ɒ��aa�C����1�̉~�`�R�C��C���Œ肵���B�~�`�R�C��C�̒��S�͌��_O�Ɉ�v���A�R�C���ʂ�x���ɐ����ł���B�~�`�R�C��C�Ɉ��̑傫���̒����d�����A�����猩�Ĕ����v���ɗ����Ď�������B�~�`�R�C��B�̒[�q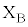 �C
�C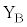 �Ԃɒ�R�lR�̓d�C��R��ڑ����A�~�`�R�C��B���ʒu
�Ԃɒ�R�lR�̓d�C��R��ڑ����A�~�`�R�C��B���ʒu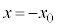 (
(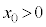 )����
)����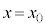 �܂œ����^��������B
�܂œ����^��������B�~�`�R�C��B�S�̂����ꂩ���͂�F�Ƃ���BF�͉E�����𐳂Ƃ���Bx��F�̊W��\���O���t�̊T�`��`���B�Ȃ��AF�̍ő�l��ŏ��l�A������Ƃ�x�̒l�������K�v�͂Ȃ��B
[��]
[3]�@�^�������Ԃƃs�X�g�����e��̒��̒P���q���q���z�C�̂Ɋւ���ȉ��̐ݖ�ɓ�����B�������A�f�M�ω��ɂ����ċC�̂̈���p�Ƒ̐�V�ɂ��ă|�A�\���̖@���u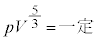 �v�����藧���Ƃ�p���Ă悢�B�C�̒萔��R�Ƃ���B��ԂƏ��Ƃ̖��C�A����уs�X�g���̎��ʂ͖����ł���B�s�X�g�����e��̊O���͐^��ł���B��Ԃ̑��x�͉E�����𐳂Ƃ���B
�v�����藧���Ƃ�p���Ă悢�B�C�̒萔��R�Ƃ���B��ԂƏ��Ƃ̖��C�A����уs�X�g���̎��ʂ͖����ł���B�s�X�g�����e��̊O���͐^��ł���B��Ԃ̑��x�͉E�����𐳂Ƃ���B
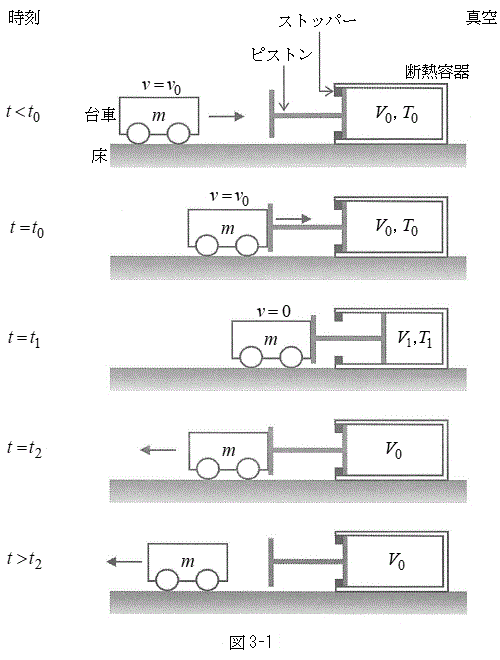 �T�@�}3-1�̂悤�ɁA�Ȃ߂炩�ɓ����s�X�g�����̒f�M�e�킪�����ȏ��ɌŒ肳��Ă���A���̗e���1�����̒P���q���q���z�C�̂���������Ă���B�͂��߁A�e����̋C�̂̑̐ς�
�T�@�}3-1�̂悤�ɁA�Ȃ߂炩�ɓ����s�X�g�����̒f�M�e�킪�����ȏ��ɌŒ肳��Ă���A���̗e���1�����̒P���q���q���z�C�̂���������Ă���B�͂��߁A�e����̋C�̂̑̐ς�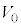 �C���x��
�C���x��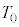 �ł���A�s�X�g���̓X�g�b�p�[�̈ʒu�ŐÎ~���Ă���B���̃s�X�g���Ɍ����Ď���m�̑�Ԃx
�ł���A�s�X�g���̓X�g�b�p�[�̈ʒu�ŐÎ~���Ă���B���̃s�X�g���Ɍ����Ď���m�̑�Ԃx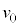 �ʼn^��������B
�ʼn^��������B���̑�Ԃ��s�X�g���ɐڂ���������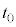 �Ƃ���B����
�Ƃ���B����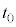 �̌�A��Ԃ̓s�X�g�����������݁A�C�̂̑̐ς�
�̌�A��Ԃ̓s�X�g�����������݁A�C�̂̑̐ς�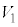 �C���x��
�C���x��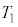 �ƂȂ����Ƃ���ő��x��0�ƂȂ����B���̎�����
�ƂȂ����Ƃ���ő��x��0�ƂȂ����B���̎�����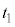 �Ƃ���B���̌�A��Ԃ̓s�X�g���ɉ����Ԃ���āA�C�̂̑̐ς�
�Ƃ���B���̌�A��Ԃ̓s�X�g���ɉ����Ԃ���āA�C�̂̑̐ς�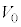 �ɖ߂�������
�ɖ߂�������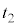 �Ńs�X�g�����痣�ꂽ�B
�Ńs�X�g�����痣�ꂽ�B
(1) ����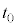 �ɂ������Ԃ̉^���G�l���M�[
�ɂ������Ԃ̉^���G�l���M�[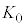 �Ɨe����̋C�̂̓����G�l���M�[
�Ɨe����̋C�̂̓����G�l���M�[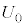 ��m�C
��m�C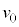 �C
�C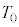 �C
�C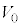 �CR�̂����K�v�Ȃ��̂�p���Ă��ꂼ��\���B
�CR�̂����K�v�Ȃ��̂�p���Ă��ꂼ��\���B
(2) 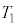 ��
��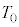 �̔�
�̔�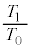 ��
��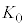 ��
��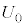 �݂̂�p���ĕ\���B
�݂̂�p���ĕ\���B
(3) 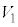 ��
��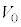 �̔�
�̔�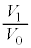 ��
��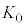 ��
��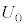 �݂̂�p���ĕ\���B
�݂̂�p���ĕ\���B 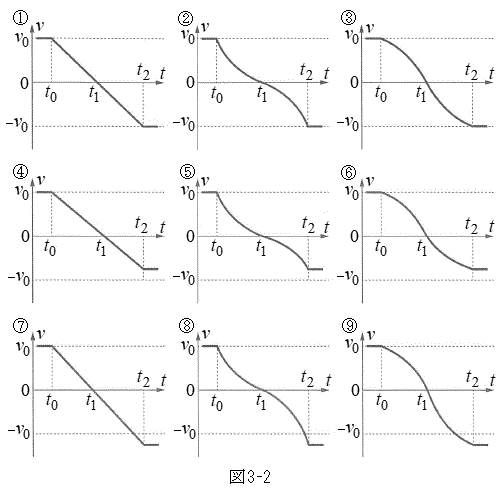 (4) ����t �Ƒ�Ԃ̑��xv�Ƃ̊W��\���O���t�Ƃ��čł��K�Ȃ��̂�}3-2�̇@�`�H�̒�����I�сA���̗��R���q�ׂ�B
(4) ����t �Ƒ�Ԃ̑��xv�Ƃ̊W��\���O���t�Ƃ��čł��K�Ȃ��̂�}3-2�̇@�`�H�̒�����I�сA���̗��R���q�ׂ�B
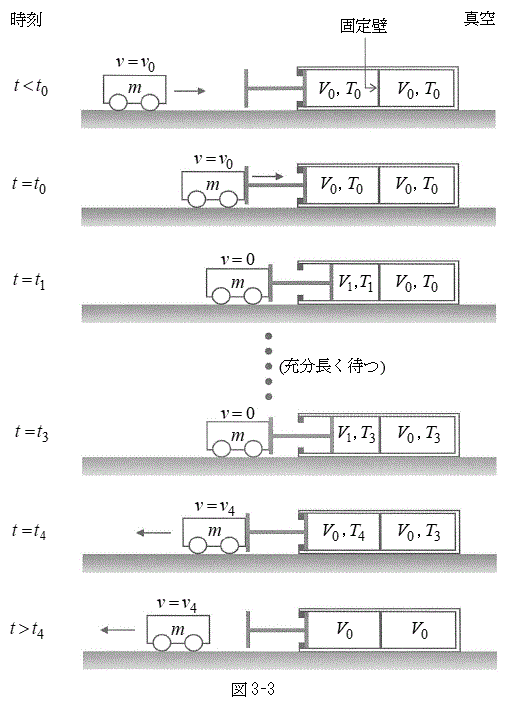 �U�@�}3-3�̂悤�ɁA�Ȃ߂炩�ɓ����s�X�g�����̒f�M�e�킪�����ȏ��ɌŒ肳��Ă���B�e��̒������Œ�ǂŎd��A���E�̗̈�ɂ��ꂼ��1�����̒P���q���q���z�C�̂������B�͂��߁A���E�̗̈���̋C�̂͂ǂ�����̐ς�
�U�@�}3-3�̂悤�ɁA�Ȃ߂炩�ɓ����s�X�g�����̒f�M�e�킪�����ȏ��ɌŒ肳��Ă���B�e��̒������Œ�ǂŎd��A���E�̗̈�ɂ��ꂼ��1�����̒P���q���q���z�C�̂������B�͂��߁A���E�̗̈���̋C�̂͂ǂ�����̐ς�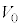 �C���x��
�C���x��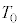 �ł���A�s�X�g���̓X�g�b�p�[�̈ʒu�ŐÎ~���Ă���B�ݖ�T�Ɠ��l�ɁA���̃s�X�g���Ɍ����Ď���m�̑�Ԃx
�ł���A�s�X�g���̓X�g�b�p�[�̈ʒu�ŐÎ~���Ă���B�ݖ�T�Ɠ��l�ɁA���̃s�X�g���Ɍ����Ď���m�̑�Ԃx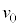 �ʼn^��������B
�ʼn^��������B��Ԃ�����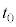 �Ńs�X�g���ɐڂ����̂��A���x��0�ɂȂ���������
�Ńs�X�g���ɐڂ����̂��A���x��0�ɂȂ���������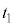 �Ƃ���B���̂Ƃ����̗̈�̋C�̂̉��x��
�Ƃ���B���̂Ƃ����̗̈�̋C�̂̉��x��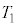 �ɂȂ����B���̎���
�ɂȂ����B���̎���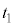 �ő�Ԃ̈ʒu���Œ肵�A���̂܂[���������ԑ҂����Ƃ���A�Œ�ǂ�ʂ����M�̈ړ��ɂ�荶�E�̗̈�̋C�̂̉��x�͂ǂ����
�ő�Ԃ̈ʒu���Œ肵�A���̂܂[���������ԑ҂����Ƃ���A�Œ�ǂ�ʂ����M�̈ړ��ɂ�荶�E�̗̈�̋C�̂̉��x�͂ǂ����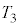 �ɂȂ����B���̂̂��A����
�ɂȂ����B���̂̂��A����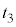 �ő�Ԃ̌Œ�����������Ƃ���A��Ԃ̓s�X�g���ɉ�����č������ɓ����n�߁A�����̗̈�̋C�̂̑̐ς�
�ő�Ԃ̌Œ�����������Ƃ���A��Ԃ̓s�X�g���ɉ�����č������ɓ����n�߁A�����̗̈�̋C�̂̑̐ς�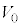 �ɖ߂�������
�ɖ߂�������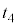 �Ńs�X�g�����痣�ꂽ�B���̂Ƃ��̑�Ԃ̑��x��
�Ńs�X�g�����痣�ꂽ�B���̂Ƃ��̑�Ԃ̑��x��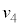 �Ƃ���B
�Ƃ���B
�s�X�g����������������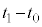 ��
��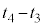 �͏[���Z���A���̊Ԃ̌Œ�ǂ�ʂ��Ă̔M�̈ړ��͖����ł���B
�͏[���Z���A���̊Ԃ̌Œ�ǂ�ʂ��Ă̔M�̈ړ��͖����ł���B
(1) ��Ԃ��s�X�g�����痣�ꂽ����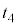 �ɂ����鍶�E�̗̈�̋C�̂̉��x�͂��ꂼ��
�ɂ����鍶�E�̗̈�̋C�̂̉��x�͂��ꂼ��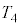 �C
�C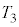 �ł������B
�ł������B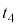 �ȍ~�̎����ɂ������Ԃ̉^���G�l���M�[
�ȍ~�̎����ɂ������Ԃ̉^���G�l���M�[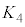 ��R�C
��R�C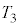 �C
�C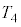 �̂����K�v�Ȃ��̂�p���ĕ\���B
�̂����K�v�Ȃ��̂�p���ĕ\���B
(2) �C�̂̉��x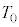 �C
�C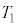 �C
�C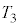 �C
�C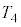 �̊Ԃɐ��藧�召�W��
�̊Ԃɐ��藧�召�W�� �̌`�ŏ����B�������AA�CB�CC�CD�ɂ͂��ꂼ��ǂ̉��x�����w�����鐔��(0�C1�C3�C4)�̂����ꂩ�ЂƂ�����A�e �ɂ� = (����)�܂��� < (�s����)������B
�ɂ� = (����)�܂��� < (�s����)������B
(3) 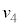 ��
��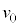 �̑傫���̔��
�̑傫���̔��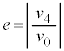 �Ƃ���B����
�Ƃ���B����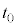 �ɂ������Ԃ̉^���G�l���M�[
�ɂ������Ԃ̉^���G�l���M�[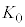 �ƍ����̗̈�̋C�̂̓����G�l���M�[
�ƍ����̗̈�̋C�̂̓����G�l���M�[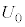 �݂̂�p����e��\���B
�݂̂�p����e��\���B [��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2025(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 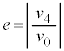 �Ƃ���B����
�Ƃ���B����