東大物理'25年前期[3]
運動する台車とピストンつき容器の中の単原子分子理想気体に関する以下の設問に答えよ。ただし、断熱変化において気体の圧力pと体積Vについてポアソンの法則「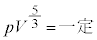 」が成り立つことを用いてよい。気体定数をRとする。台車と床との摩擦、およびピストンの質量は無視できる。ピストンつき容器の外側は真空である。台車の速度は右向きを正とする。
」が成り立つことを用いてよい。気体定数をRとする。台車と床との摩擦、およびピストンの質量は無視できる。ピストンつき容器の外側は真空である。台車の速度は右向きを正とする。
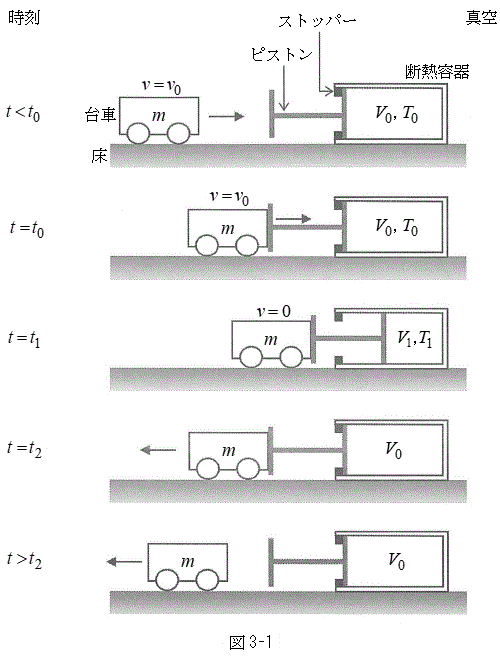 Ⅰ 図3-1のように、なめらかに動くピストンつきの断熱容器が水平な床に固定されており、この容器に1モルの単原子分子理想気体が封入されている。はじめ、容器内の気体の体積は
Ⅰ 図3-1のように、なめらかに動くピストンつきの断熱容器が水平な床に固定されており、この容器に1モルの単原子分子理想気体が封入されている。はじめ、容器内の気体の体積は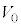 ,温度は
,温度は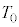 であり、ピストンはストッパーの位置で静止している。このピストンに向って質量mの台車を速度
であり、ピストンはストッパーの位置で静止している。このピストンに向って質量mの台車を速度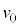 で運動させる。
で運動させる。この台車がピストンに接した時刻を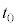 とする。時刻
とする。時刻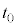 の後、台車はピストンを押し込み、気体の体積が
の後、台車はピストンを押し込み、気体の体積が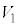 ,温度が
,温度が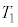 となったところで速度が0となった。この時刻を
となったところで速度が0となった。この時刻を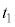 とする。その後、台車はピストンに押し返されて、気体の体積が
とする。その後、台車はピストンに押し返されて、気体の体積が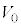 に戻った時刻
に戻った時刻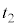 でピストンから離れた。
でピストンから離れた。
(1) 時刻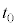 における台車の運動エネルギー
における台車の運動エネルギー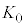 と容器内の気体の内部エネルギー
と容器内の気体の内部エネルギー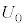 をm,
をm,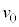 ,
,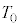 ,
,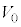 ,Rのうち必要なものを用いてそれぞれ表せ。
,Rのうち必要なものを用いてそれぞれ表せ。
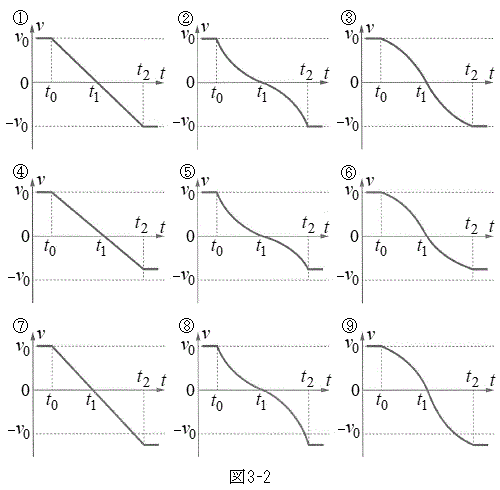 (4) 時刻t と台車の速度vとの関係を表すグラフとして最も適切なものを図3-2の①~⑨の中から選び、その理由も述べよ。
(4) 時刻t と台車の速度vとの関係を表すグラフとして最も適切なものを図3-2の①~⑨の中から選び、その理由も述べよ。
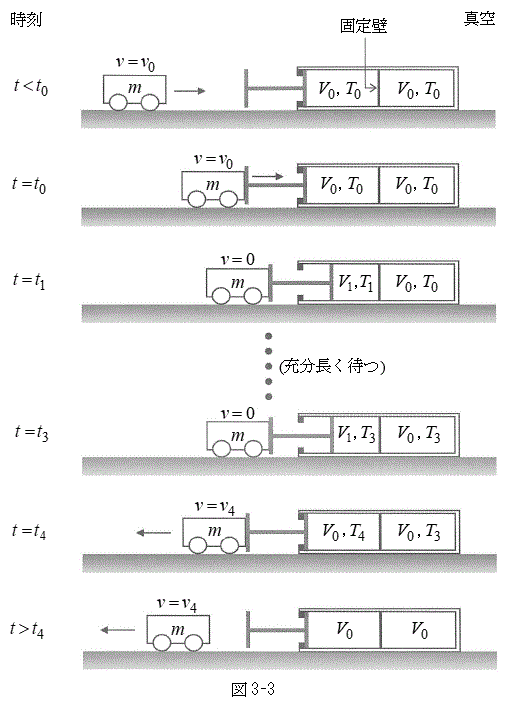 Ⅱ 図3-3のように、なめらかに動くピストンつきの断熱容器が水平な床に固定されている。容器の中央を固定壁で仕切り、左右の領域にそれぞれ1モルの単原子分子理想気体を封入した。はじめ、左右の領域内の気体はどちらも体積が
Ⅱ 図3-3のように、なめらかに動くピストンつきの断熱容器が水平な床に固定されている。容器の中央を固定壁で仕切り、左右の領域にそれぞれ1モルの単原子分子理想気体を封入した。はじめ、左右の領域内の気体はどちらも体積が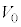 ,温度が
,温度が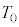 であり、ピストンはストッパーの位置で静止している。設問Ⅰと同様に、このピストンに向って質量mの台車を速度
であり、ピストンはストッパーの位置で静止している。設問Ⅰと同様に、このピストンに向って質量mの台車を速度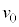 で運動させる。
で運動させる。台車が時刻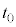 でピストンに接したのち、速度が0になった時刻を
でピストンに接したのち、速度が0になった時刻を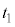 とする。このとき左の領域の気体の温度は
とする。このとき左の領域の気体の温度は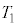 になった。この時刻
になった。この時刻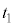 で台車の位置を固定し、そのまま充分長い時間待ったところ、固定壁を通じた熱の移動により左右の領域の気体の温度はどちらも
で台車の位置を固定し、そのまま充分長い時間待ったところ、固定壁を通じた熱の移動により左右の領域の気体の温度はどちらも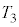 になった。こののち、時刻
になった。こののち、時刻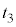 で台車の固定を解除したところ、台車はピストンに押されて左向きに動き始め、左側の領域の気体の体積が
で台車の固定を解除したところ、台車はピストンに押されて左向きに動き始め、左側の領域の気体の体積が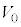 に戻った時刻
に戻った時刻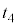 でピストンから離れた。このときの台車の速度を
でピストンから離れた。このときの台車の速度を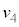 とする。
とする。
ピストンが動いていた時間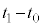 と
と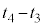 は充分短く、この間の固定壁を通じての熱の移動は無視できる。
は充分短く、この間の固定壁を通じての熱の移動は無視できる。
(1) 台車がピストンから離れた時刻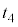 における左右の領域の気体の温度はそれぞれ
における左右の領域の気体の温度はそれぞれ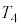 ,
,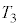 であった。
であった。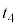 以降の時刻における台車の運動エネルギー
以降の時刻における台車の運動エネルギー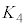 をR,
をR,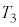 ,
,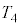 のうち必要なものを用いて表せ。
のうち必要なものを用いて表せ。
の形で書け。ただし、A,B,C,Dにはそれぞれどの温度かを指示する数字(0,1,3,4)のいずれかひとつが入り、各 には = (等号)または < (不等号)が入る。
には = (等号)または < (不等号)が入る。
(3) 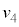 と
と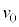 の大きさの比を
の大きさの比を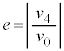 とする。時刻
とする。時刻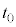 における台車の運動エネルギー
における台車の運動エネルギー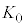 と左側の領域の気体の内部エネルギー
と左側の領域の気体の内部エネルギー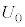 のみを用いてeを表せ。
のみを用いてeを表せ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 台車の運動と気体の融合問題ですが、Ⅰ(4),Ⅱ(3)は難問です。
(2) 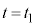 においては運動エネルギーは0,気体の内部エネルギーは
においては運動エネルギーは0,気体の内部エネルギーは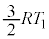 です。
です。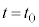 と
と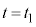 とのエネルギー保存より、
とのエネルギー保存より、 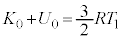 ・・・②
・・・②②÷①より、
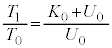 ......[答]
......[答]
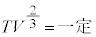 ・・・③
・・・③が得られます。
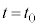 より
より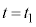 までの気体の変化は断熱変化です。③より、
までの気体の変化は断熱変化です。③より、 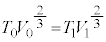 ∴
∴ 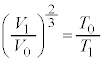
(2)の結果を用いると、
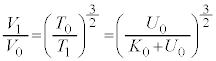 ......[答]
......[答]
(4) 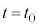 における気体の圧力を
における気体の圧力を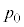 ,
,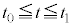 となる時刻t における気体の圧力をp,体積をVとすると、問題文のポアソンの法則を用いて、
となる時刻t における気体の圧力をp,体積をVとすると、問題文のポアソンの法則を用いて、 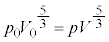 ∴
∴ 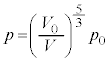 ・・・④
・・・④断熱容器の断面積をSとすると、気体がピストンを押す力(左向き)の大きさは、時刻t において、
台車の速度をvとして、
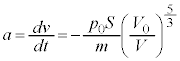 ・・・⑤
・・・⑤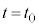 から
から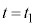 まで、⑤においてVは
まで、⑤においてVは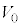 から
から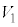 まで次第に小さくなるので、v-t グラフの接線の傾き
まで次第に小さくなるので、v-t グラフの接線の傾き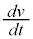 は負であって、その絶対値が次第に大きくなり、接線の傾きが次第に急になってきます。 ・・・⑥
は負であって、その絶対値が次第に大きくなり、接線の傾きが次第に急になってきます。 ・・・⑥
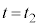 における気体の圧力を
における気体の圧力を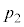 ,
,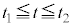 となる時刻t における気体の圧力をp,体積をVとすると、ポアソンの法則より、
となる時刻t における気体の圧力をp,体積をVとすると、ポアソンの法則より、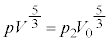 ∴
∴ 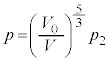 ・・・⑦
・・・⑦④,⑦で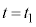 (
(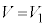 )における圧力を等しいとして、
)における圧力を等しいとして、 よって、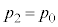 ・・・⑧
・・・⑧
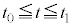 と同様にして、
と同様にして、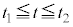 における台車の加速度a,速度vについて、
における台車の加速度a,速度vについて、 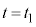 から
から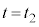 まで、Vは
まで、Vは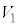 から
から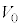 まで次第に大きくなるので、v-t グラフの接線の傾き
まで次第に大きくなるので、v-t グラフの接線の傾き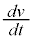 は負であって、その絶対値が次第に小さくなり、接線の傾きが次第に緩やかになってきます。 ・・・⑨
は負であって、その絶対値が次第に小さくなり、接線の傾きが次第に緩やかになってきます。 ・・・⑨
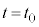 における状態方程式:
における状態方程式: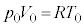
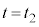 における気体の温度を
における気体の温度を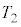 として、⑧より、状態方程式:
として、⑧より、状態方程式: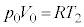
両式より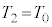
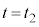 における台車の速度を
における台車の速度を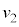 として、
として、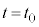 と
と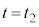 とのエネルギー保存より、
とのエネルギー保存より、台車は左向きに進んでいるので、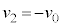 ・・・⑩
・・・⑩
⑥,⑨,⑩のようになっているグラフは、③ ......[答]理由: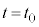 から
から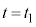 まで、グラフの接線の傾きが次第に急になり、
まで、グラフの接線の傾きが次第に急になり、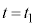 から
から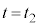 まで、接線の傾きが次第に緩やかになり、
まで、接線の傾きが次第に緩やかになり、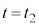 における速度が
における速度が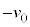 であるから。
であるから。
Ⅱ(1) 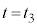 から
から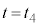 まで、右側領域の内部エネルギーに変化はありません。
まで、右側領域の内部エネルギーに変化はありません。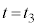 では台車の運動エネルギーは0で、
では台車の運動エネルギーは0で、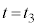 から
から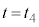 までの左側領域の内部エネルギーの減少分が
までの左側領域の内部エネルギーの減少分が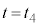 における台車の運動エネルギー
における台車の運動エネルギー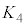 になります。
になります。 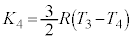 ......[答]
......[答]
(2) 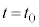 から
から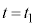 まで断熱変化で体積が減るので温度が上昇し、
まで断熱変化で体積が減るので温度が上昇し、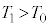 ・・・⑪
・・・⑪ 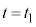 から
から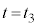 まで左側領域と右側領域合わせた気体は、外部に仕事をせず、外部との熱のやり取りもないので、熱力学第1法則より、内部エネルギーが保存します。
まで左側領域と右側領域合わせた気体は、外部に仕事をせず、外部との熱のやり取りもないので、熱力学第1法則より、内部エネルギーが保存します。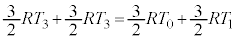 ∴
∴ 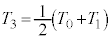 ・・・⑫
・・・⑫⑪より、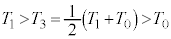 ・・・⑬
・・・⑬
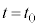 から
から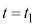 まで左側領域の気体の変化は断熱変化なので、③より、
まで左側領域の気体の変化は断熱変化なので、③より、 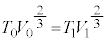 ・・・⑭
・・・⑭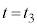 から
から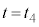 まで左側領域の気体の変化は断熱変化なので、③より、
まで左側領域の気体の変化は断熱変化なので、③より、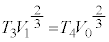 ・・・⑮
・・・⑮⑭,⑮より、
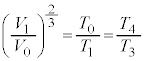 ・・・⑯
・・・⑯
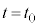 のときの左側領域の内部エネルギー
のときの左側領域の内部エネルギー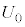 は、
は、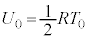 ・・・⑱
・・・⑱
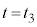 のときと
のときと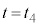 のときとのエネルギー保存より、
のときとのエネルギー保存より、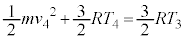 ・・・⑲
・・・⑲⑯より、
⑲より、
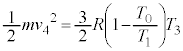 ・・・⑳
・・・⑳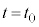 のときと
のときと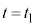 のときとのエネルギー保存より、
のときとのエネルギー保存より、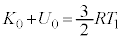 ・・・㉑
・・・㉑⑱÷㉑より、
⑳に代入して、
これを⑰で割ることにより、
∴ 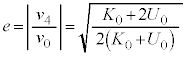 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大物理TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2025(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 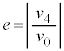 とする。時刻
とする。時刻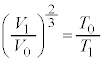
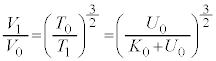 ......[答]
......[答]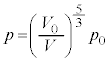 ・・・④
・・・④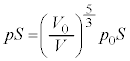
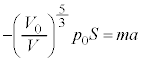
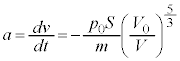 ・・・⑤
・・・⑤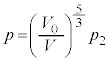 ・・・⑦
・・・⑦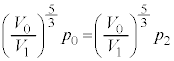
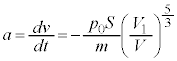
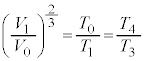 ・・・⑯
・・・⑯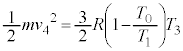 ・・・⑳
・・・⑳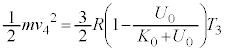
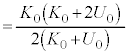
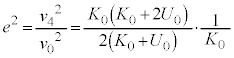
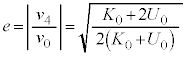 ......[答]
......[答]