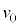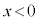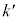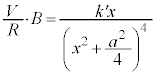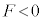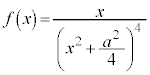東大物理'25年前期[2]
 Ⅰ 図2-1のように、真空中に直径a,長さ
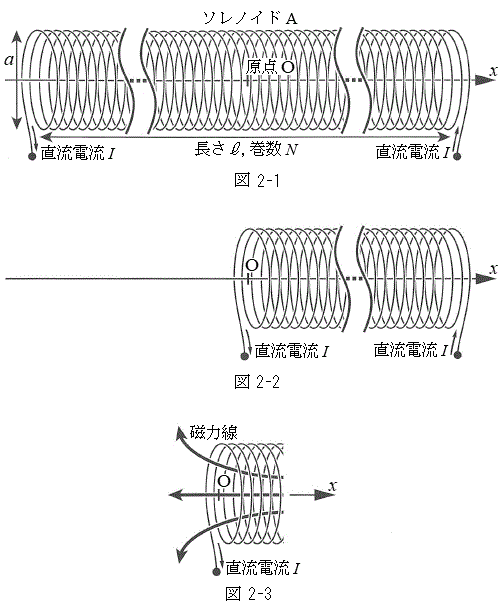
Ⅰ 図2-1のように、真空中に直径a,長さ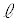 ,巻数NのソレノイドAがある。その中心軸をx軸にとり、原点OをソレノイドAの中心となるようにとった。x軸は右向きを正とする。
,巻数NのソレノイドAがある。その中心軸をx軸にとり、原点OをソレノイドAの中心となるようにとった。x軸は右向きを正とする。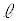 はaより十分に大きい。ソレノイドAに右から左に向けて一定の大きさIの直流電流を流す。真空の透磁率(磁気定数)を
はaより十分に大きい。ソレノイドAに右から左に向けて一定の大きさIの直流電流を流す。真空の透磁率(磁気定数)を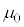 として以下の設問に答えよ。
として以下の設問に答えよ。
(1) 原点Oの磁束密度の大きさ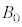 を求めよ。
を求めよ。
(2) ソレノイドAを中央で二分割して左半分(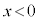 )を取り除き、図2-2のように、右から左に向けて一定の大きさIの直流電流を流した。このとき、原点O付近の磁力線は図2-3のように表される。原点Oにおける磁束密度の大きさ
)を取り除き、図2-2のように、右から左に向けて一定の大きさIの直流電流を流した。このとき、原点O付近の磁力線は図2-3のように表される。原点Oにおける磁束密度の大きさ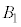 を、
を、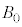 を用いて表せ。
を用いて表せ。
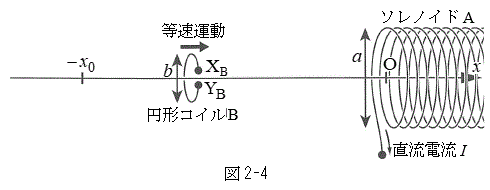 Ⅱ 図2-4のように、設問Ⅰ(1)での長さ
Ⅱ 図2-4のように、設問Ⅰ(1)での長さ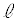 のソレノイドAを、中心軸がx軸、左端面中心が原点Oとなるように固定し、右から左に向けて一定の大きさIの直流電流を流す。さらに、直径b (
のソレノイドAを、中心軸がx軸、左端面中心が原点Oとなるように固定し、右から左に向けて一定の大きさIの直流電流を流す。さらに、直径b (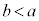 ),巻数1の円形コイルBを、位置
),巻数1の円形コイルBを、位置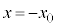 (
(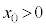 )からソレノイドA内部の位置
)からソレノイドA内部の位置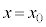 まで等速運動させる。円形コイルBの中心は常にx軸上にあり、コイル面はx軸に垂直である。
まで等速運動させる。円形コイルBの中心は常にx軸上にあり、コイル面はx軸に垂直である。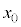 は
は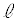 より十分に小さい。また、円形コイルBには紙面の手前側に端子
より十分に小さい。また、円形コイルBには紙面の手前側に端子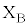 ,
,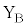 がある。その端子間距離は十分に小さく、円形コイルBの電気抵抗と自己インダクタンスは無視できる。
がある。その端子間距離は十分に小さく、円形コイルBの電気抵抗と自己インダクタンスは無視できる。
(1) 端子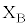 ,
,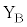 間に抵抗値Rの電気抵抗を接続し、円形コイルBを等速運動させた。円形コイルBを貫く磁束が短い時間
間に抵抗値Rの電気抵抗を接続し、円形コイルBを等速運動させた。円形コイルBを貫く磁束が短い時間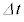 の間に
の間に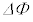 だけ変化したとき、円形コイルBに流れる電流の大きさ
だけ変化したとき、円形コイルBに流れる電流の大きさ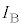 を求めよ。
を求めよ。 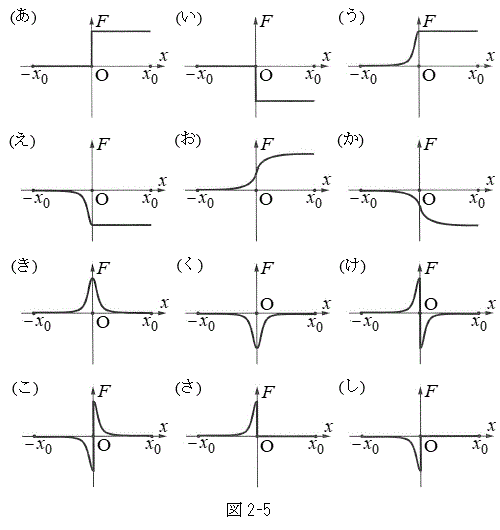 (2) 円形コイルB全体が磁場から受ける力をFとする。Fは右向きを正とする。前問Ⅱ(1)と同様に端子
(2) 円形コイルB全体が磁場から受ける力をFとする。Fは右向きを正とする。前問Ⅱ(1)と同様に端子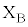 ,
,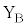 間に抵抗値Rの電気抵抗を接続し、円形コイルBを位置
間に抵抗値Rの電気抵抗を接続し、円形コイルBを位置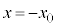 から
から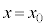 まで速さ
まで速さ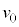 で等速運動させたとき、xとFの関係を表すグラフの概形として最も適切なものを図2-5の(あ)~(し)から一つ選んで答えよ。
で等速運動させたとき、xとFの関係を表すグラフの概形として最も適切なものを図2-5の(あ)~(し)から一つ選んで答えよ。
(3) 前問Ⅱ(2)において、電気抵抗の抵抗値をRから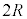 にすると、Fの大きさの最大値は何倍になるか、理由とともに答えよ。
にすると、Fの大きさの最大値は何倍になるか、理由とともに答えよ。 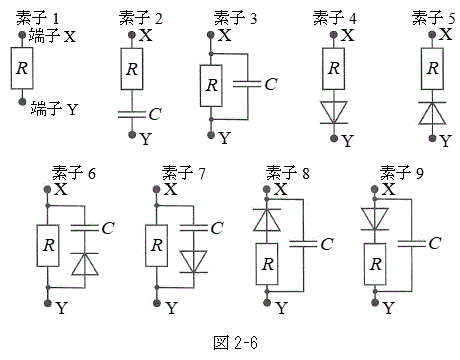 (4) 図2-6に示す素子1~9は、抵抗値Rの電気抵抗、電気容量Cのコンデンサー、ダイオードからなる。ダイオードでは、順方向には抵抗0で電流が流れ、逆方向には流れないものとする。例えば素子4においては、紙面下向きには電流が流れ、上向きには流れない。
(4) 図2-6に示す素子1~9は、抵抗値Rの電気抵抗、電気容量Cのコンデンサー、ダイオードからなる。ダイオードでは、順方向には抵抗0で電流が流れ、逆方向には流れないものとする。例えば素子4においては、紙面下向きには電流が流れ、上向きには流れない。
ソレノイドAに流す直流電流の向きを逆にし、左から右に向けて一定の大きさIの直流電流を流した。ここで、円形コイルBの端子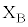 ,
,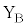 間に素子1~9のうち一つを選んで接続し、円形コイルBを位置
間に素子1~9のうち一つを選んで接続し、円形コイルBを位置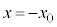 から
から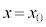 まで速さ
まで速さ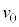 で等速運動させる場合を考える。ただし、円形コイルBの端子
で等速運動させる場合を考える。ただし、円形コイルBの端子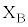 に素子の端子Xを、端子
に素子の端子Xを、端子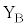 に素子の端子Yを接続するものとする。このとき、xとFの関係が、設問Ⅱ(2)と全く同じになる素子を図2-6の素子1~9からすべて選び、番号で答えよ。
に素子の端子Yを接続するものとする。このとき、xとFの関係が、設問Ⅱ(2)と全く同じになる素子を図2-6の素子1~9からすべて選び、番号で答えよ。
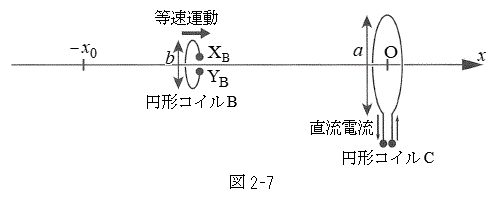 Ⅲ 図2-7のように、図2-4の状態からソレノイドAを取り除き、代わりに直径a,巻数1の円形コイルCを固定した。円形コイルCの中心は原点Oに一致し、コイル面はx軸に垂直である。円形コイルCに一定の大きさの直流電流を、左から見て反時計回りに流して磁場を作る。円形コイルBの端子
Ⅲ 図2-7のように、図2-4の状態からソレノイドAを取り除き、代わりに直径a,巻数1の円形コイルCを固定した。円形コイルCの中心は原点Oに一致し、コイル面はx軸に垂直である。円形コイルCに一定の大きさの直流電流を、左から見て反時計回りに流して磁場を作る。円形コイルBの端子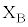 ,
,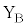 間に抵抗値Rの電気抵抗を接続し、円形コイルBを位置
間に抵抗値Rの電気抵抗を接続し、円形コイルBを位置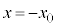 (
(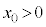 )から
)から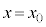 まで等速運動させる。
まで等速運動させる。円形コイルB全体が磁場から受ける力をFとする。Fは右向きを正とする。xとFの関係を表すグラフの概形を描け。なお、Fの最大値や最小値、それをとるxの値を示す必要はない。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 磁気に関する基本問題ですが、物理的思考力を要求する内容になっています。
Ⅰ(1) 原点Oにおける磁場の強さHは、単位長さあたりの巻数が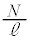 なので(電流の作る磁界を参照)、
なので(電流の作る磁界を参照)、 原点Oにおける磁束密度の大きさ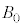 は、真空中では
は、真空中では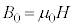 より、
より、 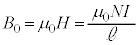 ......[答]
......[答]
(2) ソレノイドの右半分が原点Oに作る磁束密度を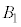 ,取り除かれたソレノイドの左半分が原点Oに作る磁束密度を
,取り除かれたソレノイドの左半分が原点Oに作る磁束密度を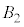 とすると、
とすると、
Ⅱ(1) 電磁誘導の法則より、円形コイルBに発生する起電力の大きさは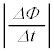 です。端子
です。端子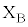 ,
,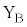 間に抵抗Rを接続すると、円形コイルBに流れる電流の大きさ
間に抵抗Rを接続すると、円形コイルBに流れる電流の大きさ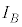 は、オームの法則より、
は、オームの法則より、 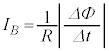 ......[答]
......[答]
(2) ソレノイドAの左端にできる磁場は図2-3のようになり、原点Oからx軸負方向に進むに従って磁力線の密度は小さくなり、磁束密度の大きさも小さくなります。
円形コイルBを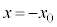 から
から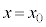 (
(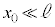 )まで等速運動させると、円形コイルBを貫く磁束は増大を続け、ソレノイドの中に入ると、磁束は次第に一定になります。変化率の大きさ
)まで等速運動させると、円形コイルBを貫く磁束は増大を続け、ソレノイドの中に入ると、磁束は次第に一定になります。変化率の大きさ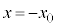 は原点Oまで増加しますが、原点Oを過ぎると減少して0に近づきます。
は原点Oまで増加しますが、原点Oを過ぎると減少して0に近づきます。
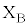 から原点Oまで、抵抗Rを接続した円形コイルBに流れる電流は、レンツの法則より、増大する左向きの磁場を弱める向き、つまりx軸正方向の磁場を強める向き、即ち、端子
から原点Oまで、抵抗Rを接続した円形コイルBに流れる電流は、レンツの法則より、増大する左向きの磁場を弱める向き、つまりx軸正方向の磁場を強める向き、即ち、端子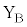 から端子
から端子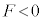 に向って流れ、x軸正方向に向く磁場を作り、ソレノイドの作る磁場との間に斥力、つまりx軸負方向の力を生じます。つまり
に向って流れ、x軸正方向に向く磁場を作り、ソレノイドの作る磁場との間に斥力、つまりx軸負方向の力を生じます。つまり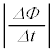 です。また、Fの大きさは、原点Oまで、磁場の強さと
です。また、Fの大きさは、原点Oまで、磁場の強さと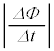 の増大とともに次第に増大します(負値のFは小さくなります、フレミング左手の法則を参照)。
の増大とともに次第に増大します(負値のFは小さくなります、フレミング左手の法則を参照)。
原点Oを通過しても、円形コイルBを貫く磁束は増大を続け、Bに流れる電流の向き、Bが受ける力の向きは変わりませんが、Bが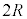 に近づくに従って、ソレノイドA内の磁場は次第に一定値に近づき、
に近づくに従って、ソレノイドA内の磁場は次第に一定値に近づき、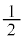 は減少して0に近づき、即ち左向きの力Fの大きさも小さくなります。
は減少して0に近づき、即ち左向きの力Fの大きさも小さくなります。
そうなっているグラフは(く) ......[答]
(3) 抵抗値をRから にすると、各時点で円形コイルBを流れる電流の大きさは
にすると、各時点で円形コイルBを流れる電流の大きさは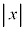 倍になり、磁場の値が同じ値であれば、Fの大きさは電流の大きさに比例するので、Fの最大値も
倍になり、磁場の値が同じ値であれば、Fの大きさは電流の大きさに比例するので、Fの最大値も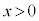 倍になります。 ......[答]
倍になります。 ......[答]
(4) ソレノイドAに流す電流の向きを逆にすると、コイルBに流れる電流の向きも逆になり、各素子にYからXに向って電流を流そうとします。ですが、ソレノイドの作る磁場とコイルBの作る磁場との間に左向きの力が働くことは変わりません。
素子2,素子3,素子6,素子8、素子9では、コンデンサーに充電されるので(2)とは違う状況になります。素子4では電流が流れず(2)とは違う状況です。
素子5では、YからXに向って抵抗Rを通して電流が流れ、(2)と同じ状況になります。
素子7では、コンデンサーに向って電流が流れず充電は起こりません。素子7は(2)と同じ状況になります。
よって、(2)と同じ状況になる素子は、1,5,7 ......[答]
Ⅲ 円形コイルCが作る磁場の磁力線は、図2-3と同様に考えると、x軸負方向を向き、磁力線の密度は原点Oで最も大きく、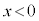 が大きくなるに従って小さくなります。また、磁場の強さは
が大きくなるに従って小さくなります。また、磁場の強さは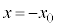 と
と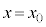 とで対称になります。円形コイルBを
とで対称になります。円形コイルBを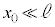 から
から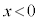 (
(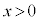 )まで等速運動させると、円形コイルCとの間に、
)まで等速運動させると、円形コイルCとの間に、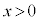 では斥力、
では斥力、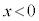 では引力が働きますが、力はずっとx軸負方向を向き、力の大きさも
では引力が働きますが、力はずっとx軸負方向を向き、力の大きさも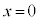 と
と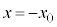 とで対称になります。
とで対称になります。 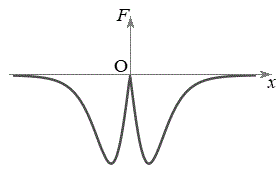 また、
また、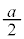 付近では、円形コイルCが作る磁場の強さが最大値に近づき磁束の変化率が0に近づくので、円形コイルBに生じる起電力が一旦0となり、力の大きさも一旦0になります。つまり、
付近では、円形コイルCが作る磁場の強さが最大値に近づき磁束の変化率が0に近づくので、円形コイルBに生じる起電力が一旦0となり、力の大きさも一旦0になります。つまり、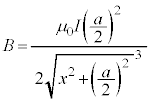 から原点Oまでの間にFの大きさが最大になるところがあり、そこから原点に近づくに従って、Fの大きさは次第に小さくなり0になります。
から原点Oまでの間にFの大きさが最大になるところがあり、そこから原点に近づくに従って、Fの大きさは次第に小さくなり0になります。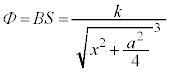 でも同様です。よって、xとFの関係を表すグラフの概形は右図。
でも同様です。よって、xとFの関係を表すグラフの概形は右図。
注.円形コイルCに大きさIの電流が流れるとき、半径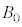 の円形コイルCがx軸上の位置xに作る磁束密度の大きさBは、
の円形コイルCがx軸上の位置xに作る磁束密度の大きさBは、 となることが知られています(円電流の作る磁界を参照)。円形コイルBの面積をSとして、円形コイルBを貫く磁束Φは、kを定数として、 と書けます。円形コイル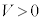 の等速運動の速さを
の等速運動の速さを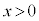 とすると、円形コイルBに発生する起電力Vは、
とすると、円形コイルBに発生する起電力Vは、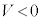 において
において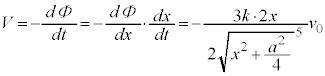 ,
,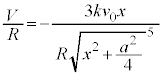 において
において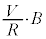 として、
として、 円形コイルBに流れる電流は、
円形コイルが磁場から受ける力Fは、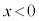 に比例し、
に比例し、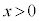 を定数として、
を定数として、 という形になるのですが、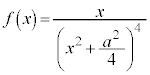 ではBとCの間に斥力、
ではBとCの間に斥力、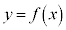 ではBとCの間に引力が働き、いずれも
ではBとCの間に引力が働き、いずれも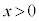 となります。
となります。 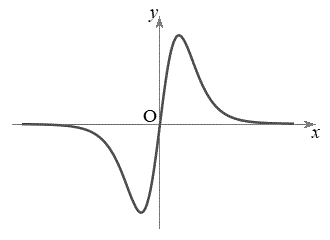 として、
として、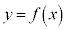 のグラフは右図のようになりますが、力Fのグラフの概形は、右図で
のグラフは右図のようになりますが、力Fのグラフの概形は、右図で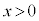 の部分をy軸に関して折り返したものになります。
の部分をy軸に関して折り返したものになります。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大物理TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。なお、解答は、
苦学楽学塾制作です。©2005-2026(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 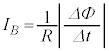 ......[答]
......[答]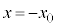 は原点Oまで増加しますが、原点Oを過ぎると減少して0に近づきます。
は原点Oまで増加しますが、原点Oを過ぎると減少して0に近づきます。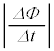 の増大とともに次第に増大します(負値のFは小さくなります、フレミング左手の法則を参照)。
の増大とともに次第に増大します(負値のFは小さくなります、フレミング左手の法則を参照)。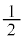 は減少して0に近づき、即ち左向きの力Fの大きさも小さくなります。
は減少して0に近づき、即ち左向きの力Fの大きさも小さくなります。